Unit-1
Introduction to Graph Theory
The analysis of lines and points is Graph Theory.
It is a mathematics sub-field that deals with graphs: diagrams that contain points and lines and that also represent mathematical truths in a pictorial way. The theory of graphs is the analysis of the interaction of edges and vertices. A graph is formally a pair (V, E), where a finite set of vertices is V and a finite set of edges is E.
|
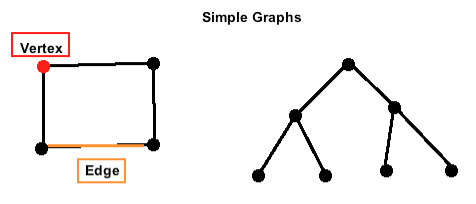
Figure 1
1.1.1 Definitions
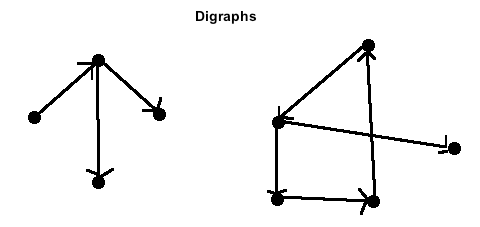
An arc is a line that is directed (a pair of ordered vertices).
The line connecting a pair of nodes is an edge.
The edges of an incident are edges that share a vertex. If the edge ties the vertex to another, an edge and a vertex exist.
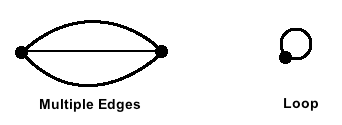
An edge or arc that joins a vertex to itself is a loop.
A point or circle is a vertex, also called a node. It is the basic unit from which graphs are generated.
Vertices which are connected by an edge are adjacent vertices.
A vertex's degree is essentially the number of edges connected to the vertex. Twice the loops count.
The node (vertex) previous to a given vertex on a path is a predecessor.
The node (vertex) which follows a given vertex on a path is a successor.
A walk is a sequence of edges and vertices.
For every edge distinct, a circuit is a closed walk.
A closed walk is a walk back to itself from a vertex; a sequence of vertices and edges starting and ending at the same location.
A cycle is a closed walk without repeating vertices (except that the first and last vertices are the same).
A road is a walk where the vertices are not replicated. A route u-v is a path starting at u and terminating at v.
A walk with u-v will be a walk starting at u and stopping at v.
By combining the two vertices he used to merge, an edge contraction involves removing an edge from a graph.
A graph traversal in computer science and computer-based graph theory is an analysis of a graph in which one by one the vertices are visited or modified.
A Hamiltonian cycle is a loop that is closed where each node is visited precisely once.
1.2.1 Acyclic directed graph
A finite directed graph that has no driven cycles is an acyclic directed graph.
1.2.2 Directed graph
A directed graph is a graph where the edges have direction; that is, pairs of vertices are ordered.
|
Figure 2
1.2.3 Multigraph
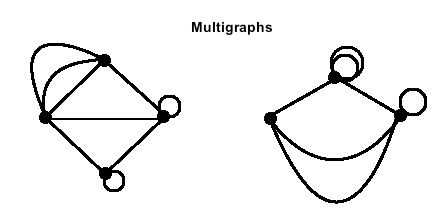
The graph that occurs when you delete several edges is a condensation of a multigraph, leaving just one edge at any two points.
A multigraph is a loop-less graph, but which may have several edges.
|
Figure 3
A graph with no edges is a null graph. Maybe it has one or two vertices.
|
Figure 4
An oriented graph is a led graph with no symmetrical pairs of directed edges.
The graph is called a related graph if a graph has a path between each pair of vertices (there is no vertex not connected to an edge).
If, through repeated edge contractions or deletions, a graph G 'can be constructed from a graph G, the graph G' is a graph minor of G.
1.2.4 Inverted Graph
A graph with the same vertices but none of the same edges is an inverted graph G 'of G; two vertices in G' are adjacent if and only if in G they were not adjacent.
1.2.5 Plain graph
A plain graph is a graph with no loops or many edges at all. No multiple edges implies that the same endpoints are not visible on two edges.
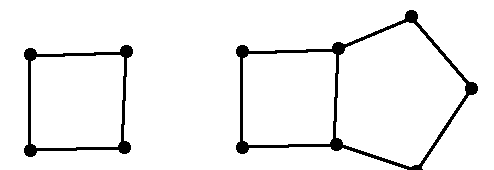
1.2.6 Subgraph
A subgraph is a graph whose vertices and edges are part of another graph's vertices and edges (the supergraph).
1.2.7 Symmetric graph
A symmetric graph is a D-directed graph where the inverted arc (y,x) is also in D for each arc (x,y).
1.2.8 Trivial Graph
A graph with just a single vertex is a trivial graph.
1.2.9 Undirected graph
An undirected graph is a graph where no path is given to any of the edges; the pairs of vertices representing each edge are unordered.
1.2.10 Subgraphs
A Subgraph Q of a graph R is a graph whose vertex set V(Q) is a subset of the vertex set V(R), that is V(Q)⊆V(R), and whose edge set E(Q) is a subset of the edge set E(R), that is E(Q)⊆E(R).
|
Q (Subgraph of R) R
Let 'G-' be a simple graph with some vertices like 'G' and in 'G-' there is an edge {U, V}, if the edge is not present in G. This means that two vertices in 'G' are adjacent if the two vertices in G are not adjacent.
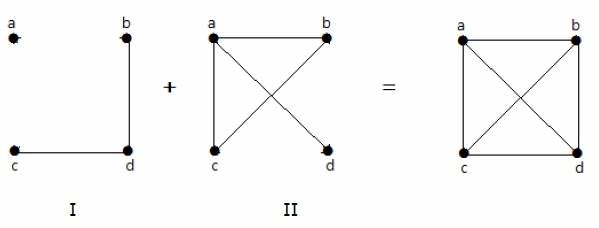
If in another graph II, the edges existing in graph I are absent, and if both graph I and graph II are combined to form a complete graph, then graph I and graph II are referred to as mutual complements.
|
Figure 4
Notice − A mixture of two additional graphs produces a complete graph.
If 'G' is any simple graph, then |E(G)| + |E('G-')| = |E(Kn)|, where n = number of vertices in the graph. |
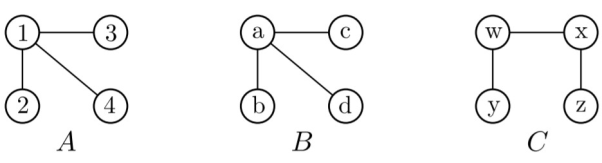
Graph isomorphism is an equivalence relationship on graphs which, as such, splits the class into equivalence groups on all graphs. An isomorphism class of graphs is called a group of graphs isomorphic to one another. The two graphs shown below are isomorphic, despite their different looking drawings.
|
Figure 5
Two isomorphic plots A and B and one non-isomorphic plot C; Each of them has four vertices with three corners.
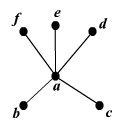
The degree of a vertex, in graph theory, is the number of edges connecting it. Vertex a has degree 5 in the following example, and the rest has degree 1. A degree 1 vertex is referred to as a "end vertex"
|
Figure 6
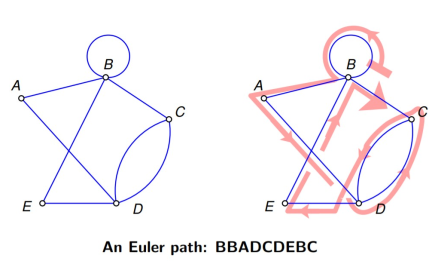
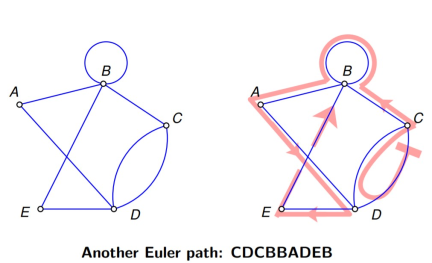
Euler path and Euler circuits
An Euler path is a path that uses any graph edge once precisely.
|
Figure 7
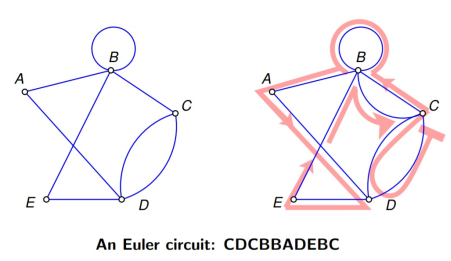
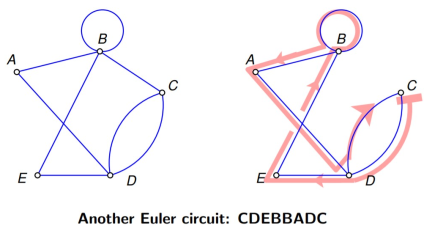
An Euler circuit is a circuit that uses each graph edge once precisely.
|
Figure 8
An Euler path begins and finishes at multiple vertices.
The circuit of An Euler begins and ends at the same vertex.
References
1. D.S. Chandrasekharaiah: Graph Theory and Combinatorics, Prism,2005.
2. Chartrand Zhang: Introduction to Graph Theory, TMH, 2006.
3. Richard A. Brualdi: Introductory Combinatorics, 4th Edition, Pearson Education, 2004.
4. Geir Agnarsson & Raymond Geenlaw: Graph Theory, Pearson Education, 2007.