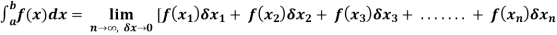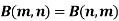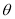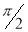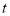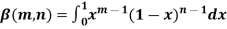Module-3
Integral Calculus
Double integral –
Before studying about multiple integrals , first let’s go through the definition of definition of definite integrals for function of single variable.
As we know, the integral
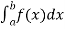
Where is belongs to the limit a ≤ x ≤ b
This integral can be written as follows-
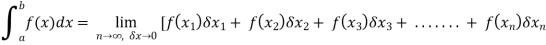
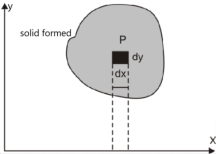
Now suppose we have a function f(x , y) of two variables x and y in two dimensional finite region Rin xy-plane.
Then the double integration over region R can be evaluated by two successive integration
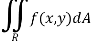
Evaluation of double integrals-
If A is described as 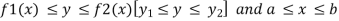
Then,
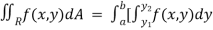 ]dx
]dx
Let do some examples to understand more about double integration-
Example-: Evaluate  , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
Sol. Let , I = 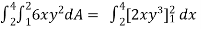
= 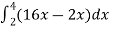
= 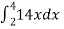
= 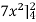
= 84 sq. Unit.
Which is the required area,
Example-2: Evaluate 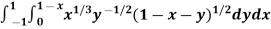
Sol. Let us suppose the integral is I,
I = 
Put c = 1 – x in I, we get
I = 
Suppose, y = ct
Then dy = c
Now we get,
I = 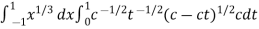
I = 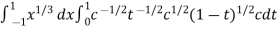
I = 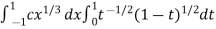
I = 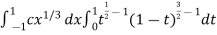
I =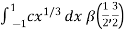
As we know that by beta function,
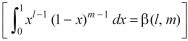
Which gives,
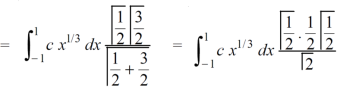
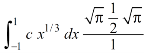
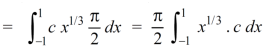
Now put the value of c, we get
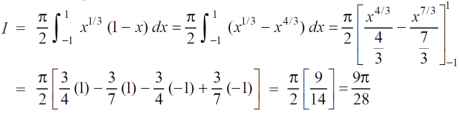
Example-3: Evaluate the following double integral,
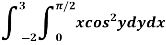
Sol. Let,
I = 
On solving the integral, we get
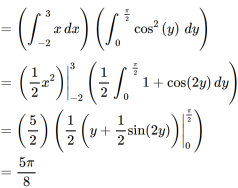
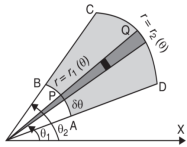
Double integration in polar coordination -
In polar coordinates, we need to evaluate
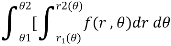
Over the region bounded by θ1 and θ2.
And the curves r1(θ) and r2(θ)
Example-1: Evaluate the following by changing to polar coordinates,
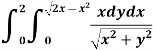
Sol. In this problem, the limits for y are 0 to 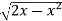 and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 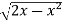
Squaring both sides,
y² = 2x - x²
x² + y² = 2x
But in polar coordinates,
We have,
r² = 2r cosθ
r = 2 cosθ
From the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cosθ and y by r sinθ, dy dx by r drdθ,
We get,

Example-2: Evaluate the following integral by converting into polar coordinates.
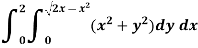
Sol. Here limits of y,
y = 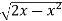
y² = 2x - x²
x² + y² = 2x
x² + y² - 2x = 0 ………………(1)
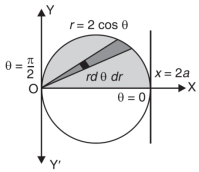
Eq. (1) represent a circle whose radius is 1 and centre is ( 1, 0)
Lower limit of y is zero.
Region of integration in upper half circle,
First we will covert into polar coordinates,
By putting
x by r cos θ and y by r sinθ , dy dx by r drdθ,
Limits of r are 0 to 2 cosθ and limits of θ are from 0 to π / 2.

Example-3: Evaluate 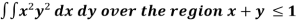
Sol. Let the integral,
I = 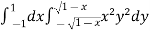
=

Put x = sinθ
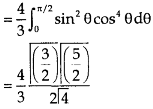
= π / 24 ans.
Triple integrals
Definition: Let f(x,y,z) be a function which is continuous at every point of the finite region (Volume V) of three dimensional space. Divide the region V into n sub regions of respective volumes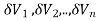 . Let (
. Let (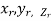 ) be a point in the
) be a point in the  sub region then the sum:
sub region then the sum:
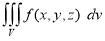 =
= 
Is called triple integration of f(x, y, z) over the region V provided limit on R.H.S of above Equation exists.

Example-1: Evaluate
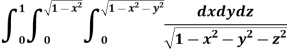
Solution:
Let
I = 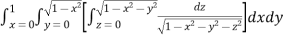
= 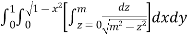
(Assuming m =  )
)
=  dxdy
dxdy
= 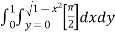
=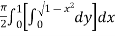
= 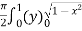 dx
dx
= 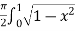 dx
dx
= 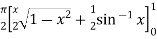
=
I =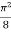
Example-2: Evaluate 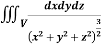 Where V is annulus between the spheres
Where V is annulus between the spheres  and
and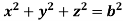 (
(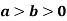 )
)
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
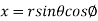 ,
, 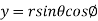 ,
, 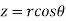
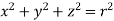 , dxdydz =
, dxdydz = 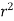 sin
sin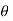 drd
drd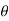 d
d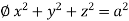 ,
,
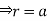 and
and 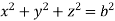
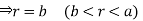
For the positive octant, r varies from r =b to r =a , 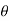 varies from
varies from 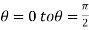 and
and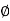 varies from
varies from 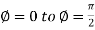
I= 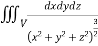
= 8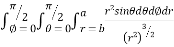
=8
=8
=8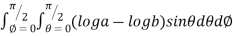
=8 log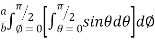
= 8 log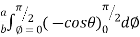
I= 8 log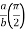
I = 4 log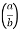
Example-3: Evaluate
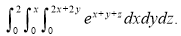
Solution:-
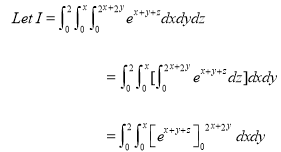
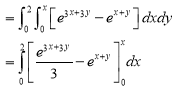


Ex.4: Evaluate-
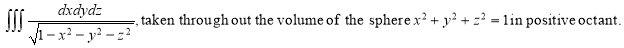
Solution:-
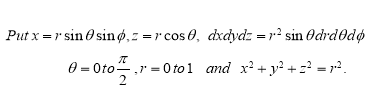
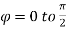
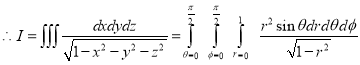


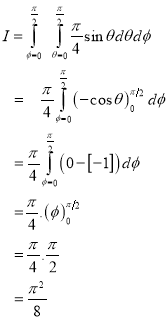
The limits of integration change when we change the order of integration.
We draw the rough diagram of the region of integration to find the new limits.
Example-1: Change the order of integration in the double integral-
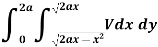
Sol.
Limits are given-
x = 0, x = 2a
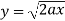
And
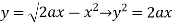
And
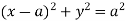
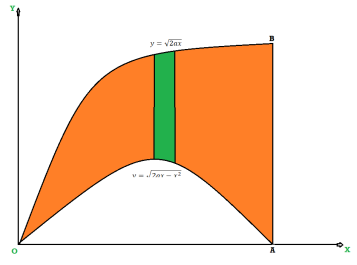
The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,
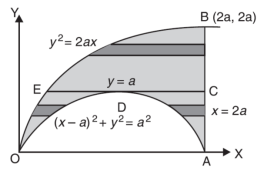
Now-
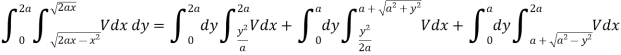
Which is the required answer.
Example: Change the order of integration in-

Sol.
The limits are given as-

It means-
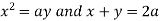
Also
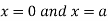
Now we have here-
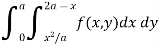
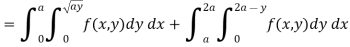
Example-2: Change the order of integration for the integral 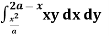 and evaluate the same with reversed order of integration.
and evaluate the same with reversed order of integration.
Sol:
 Given, I =
Given, I =  …(1)
…(1)
In the given integration, limits are
y =  , y = 2a – x and x = 0, x = a
, y = 2a – x and x = 0, x = a
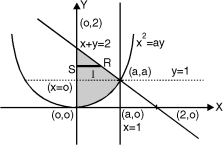
The region bounded by x2 = ay, x + y = 2a Fig.6.5
And x = 0, x = a is as shown in Fig. 6.5
Here we have to change order of Integration. Given the strip is vertical.
Now take horizontal strip SR.
To take total region, Divide region into two parts by taking line y = a.
1 st Region:
Along strip, y constant and x varies from x = 0 to x = 2a – y. Slide strip IIelto x-axis therefore y varies from y = a to y = 2a.
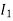 = dyxy dx .....…(2)
= dyxy dx .....…(2)
2nd Region:
Along strip, y constant and x varies from x = 0 to x= . Slide strip IIel to x-axis therefore x-varies from y = 0 to y = a.
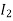 = dyxy dx …(3)
= dyxy dx …(3)
From Equation (1), (2) and (3),
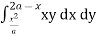 = dyxy dx + dyxy dx
= dyxy dx + dyxy dx
= 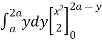 + y dy
+ y dy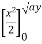
=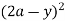 dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2dy
dy + (ay) dy = y (4a2 – 4ay + y2) dy + ay2dy
= (4a2 y – 4ay2 + y3) dy + y2dy
= 
= 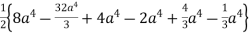 +
+ 
= a4
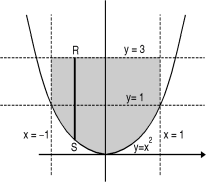
Example-4: Express as single integral and evaluate dy dx + dy dx.
 Sol:
Sol:
Given: I = dy dx + dy dx
I = I1 + I2
The limits of region of integration I1 are
x = – ; x = and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.
The region of integration are as shown in Fig
To consider the complete region take a vertical strip SR along the strip y varies from y to y = 3 and x varies from x = –1 to x = 1.
I = 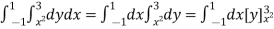


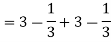
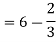

Key takeaways-
2. 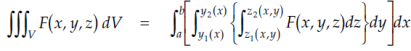
Area of double integration
Area in Cartesian coordinates-
Example-1: Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
Sol. Let,
y = 2 – x ………………..(1)
And y² = 2 (2 – x) ………………..(2)
On solving eq. (1) and (2)
We get the intersection points (2,0) and (0,2) ,
We know that,
Area = 
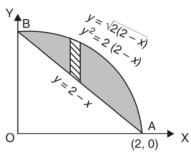
Here we will find the area as below,
Area = 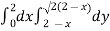
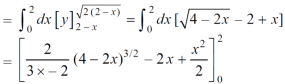
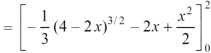
Which gives,
= ( - 4 + 4 /2 ) + 8 / 3 = 2 / 3.
Example-2: Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
Sol. Let,
y² = 4ax ………………..(1)
And
x² = 4ay…………………..(2)
Then if we solve these equations , we get the values of points where these two curves intersect
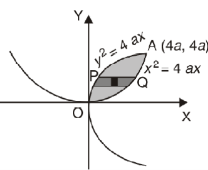
x varies from y²/4a to  and y varies from o to 4a,
and y varies from o to 4a,
Now using the conceot of double integral,
Area = 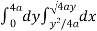
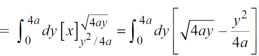
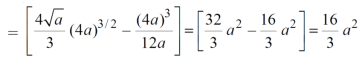
Area in polar coordinates-
Example-3: Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
Sol. We have,
r = a(1+cosθ) …………………….(1)
And
r = a ……………………………….(2)
On solving these equations by eliminating r , we get
a(1+cosθ) = a
(1+cosθ) = 1
Cosθ = 0
Here a θ varies from – π/2 to π/2
Limit of r will be a and 1+cosθ)
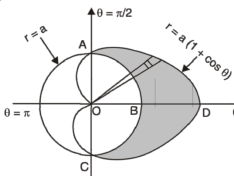
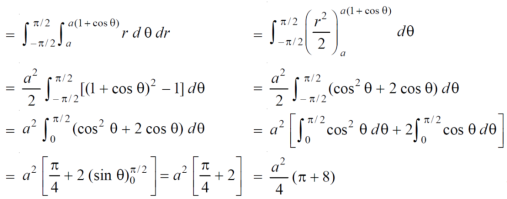
Which is the required area.
Example-4: Find the are lying inside a cardioid r = 1 + cosθ and outside the parabola r(1 + cosθ) = 1.
Sol. Let,
r = 1 + cosθ ……………………..(1)
r(1 + cosθ) = 1……………………..(2)
Solving these equations, we get
(1 + cosθ )(1 + cosθ ) = 1
(1 + cosθ )² = 1
1 + cosθ = 1
Cosθ = 0
θ = ±π / 2
So that, limits of r are,
1 + cosθ and 1 / 1 + cosθ
The area can be founded as below,

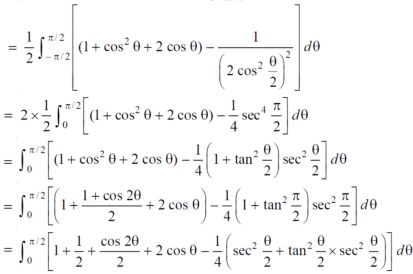
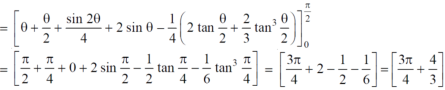
Double integrals as volumes
Suppose we have a curve y = f(x) is revolved about an axis , then a solid is generated , now we need to find out the volume of the solid generated ,
The formula for volume of the solid generated about x-axis,
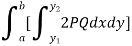
Example-1: Calculate the volume generated by the revolution of a cardioid,
r = a ( 1 – cosθ) about its axis
Sol. Here,
r = a ( 1 – cosθ)
Volume = 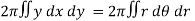

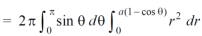
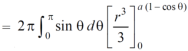
=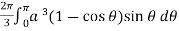
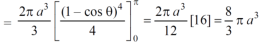
Which is the volume of generated by cardioid.
Example-2: Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
Sol. We know that,
Volume = 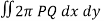
Here , PQ = 3 – x,
= 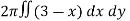
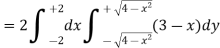
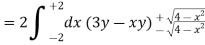
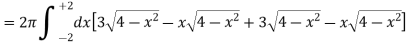
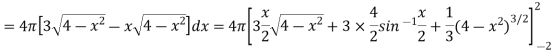
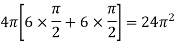
The volume is 24π².
Example-3: Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and -x ≤ y ≤ x
Sol. The is a double integral of z = 3 + x² - 2y over the region R.
Volume will be,
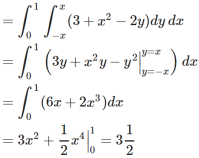
CENTER OF MASS AND GRAVITY-
Centre of mass-
We have-

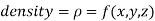
Mass = volume 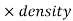
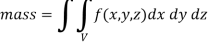
Example: Find the mass of a plate formed by the coordinate planes and the plane-
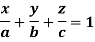
The variable density 
Sol.
Here we the mass will be-
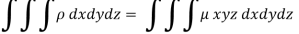
The limits of y are from y = 0 to y = b(1 – x/a) and limits of x are from 0 to a.
Therefore the required mass will be-
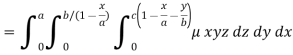
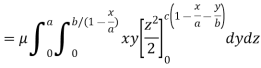
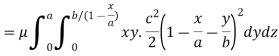
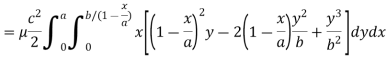

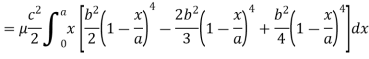
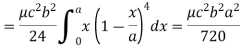
Which is the required answer.
Centre of gravity-
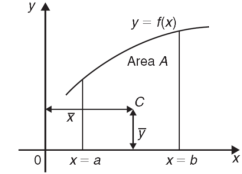
The centre of gravity of a lamina is the point where it balances perfectly which means the lamina’s centre of mass.
If 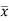 and
and 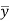 are the coordinates of the centroid C of area A, then-
are the coordinates of the centroid C of area A, then-
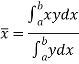
And
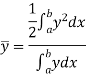
Example: Determine the coordinates of the centroid of the area lying between the curve y = 5x - x² and the x-axis.
Sol.
Here y = 5x - x²when y = 0, x = 0 or x = 5
Therefore the curve cuts the x-axis at 0 and 5 as in the figure-
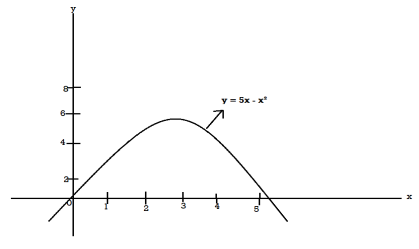


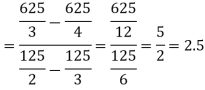
Now
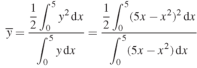
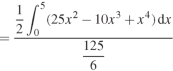

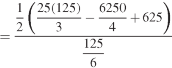
= 2.5
Therefore the centroid of the area lies at (2.5, 2.5)
Key takeaways-
- Centre of mass-
We have-
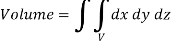
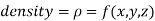
Mass = volume 
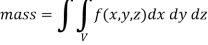
The beta and gamma functions are defined as-
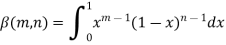
And
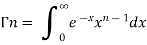
These integrals are also known as first and second Eulerian integrals.
Note- Beta function is symmetrical with respect to m and n.

Some important results-
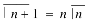
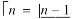
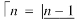
Ex.1: Evaluate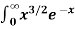 dx
dx
Solution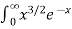 dx =
dx = 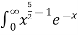 dx
dx
= γ(5/2)
= γ(3/2+ 1)
= 3/2 γ(3/2 )
= 3/2. ½ γ(½ )
= 3/2. ½ π
= ¾ π
Ex. 2: Find γ(-½)
Solution: (-½) + 1= ½
γ(-1/2) = γ(-½ + 1) / (-½)
= - 2 γ(1/2 )
= - 2 π
Ex. 3. Show that 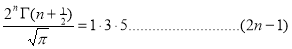

Solution:
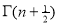 =
= 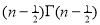
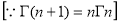
= 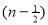
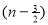
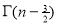
= 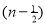

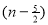
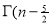 ) .......................
) .......................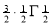
= 

= 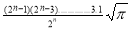

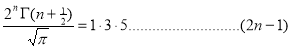
Ex. 4: Evaluate 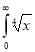
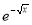 dx.
dx.
Solution: Let 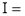
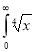
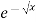 dx
dx
X | 0 |  |
T | 0 | 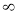 |
Put 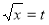 or
or  ; dx =2t dt .
; dx =2t dt .
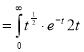 dt
dt
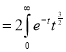 dt
dt
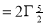
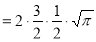
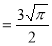
Ex. 5: Evaluate 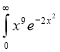 dx.
dx.
Solution: Let 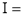
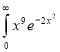 dx.
dx.
X | 0 | 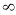 |
T | 0 |  |
Put 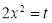 or
or 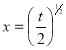 ; 4x dx = dt
; 4x dx = dt
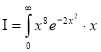 dx
dx
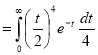

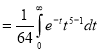
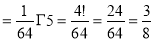
Evaluation of beta function 𝛃 (m, n)-
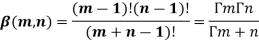
Here we have-
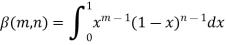
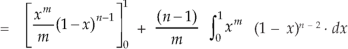
Or
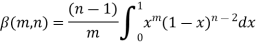
Again integrate by parts, we get-
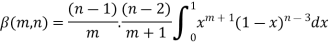
Repeating the process above, integrating by parts we get-
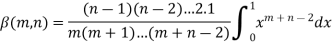
Or
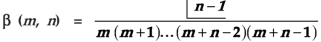
Evaluation of gamma function-
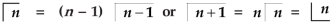
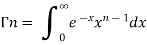
Integrating by parts, we take 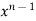 as first function-
as first function-
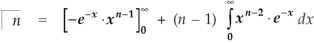
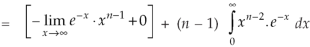
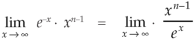

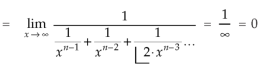
We get-
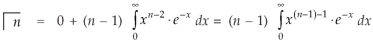
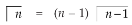
Replace n by n+1,
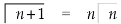
Relation between beta and gamma function-
We know that-
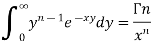
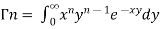 ………… (1)
………… (1)
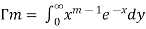 …………………..(2)
…………………..(2)
Multiply equation (1) by 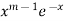 , we get-
, we get-
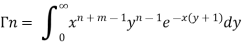
Integrate both sides with respect to x within limits x = 0 to x = 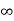 , we get-
, we get-
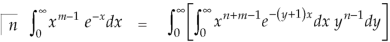
But
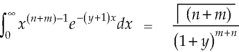
By putting λ = 1 + y and n = m + n
We get by using this result in (2)-
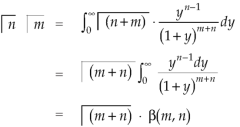
So that-
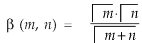
Definition : Beta function 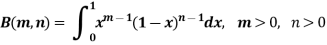
|
Properties of Beta function : |
2. 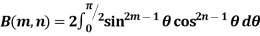 |
3. 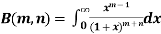 |
4. 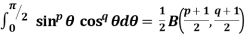 |
Example(1): Evaluate
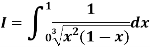
Solution:
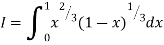
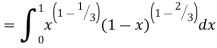
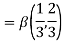
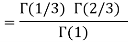
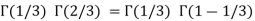
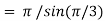
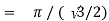
= 2 π/3
BETA FUNCTION MORE PROBLEMS
Relation between Beta and Gamma functions :
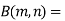 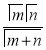
| ||||||
Example(3): Prove that 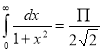 Solution : Let 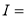 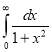 Put    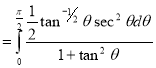 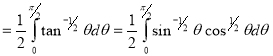 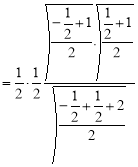 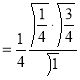 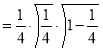 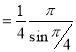 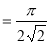  Example(4): Evaluate 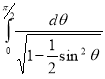 Solution :Let 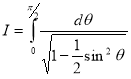 Put 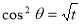 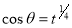  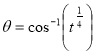 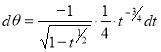 When 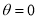 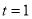 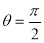 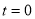 Also 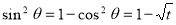
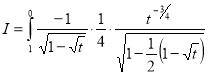 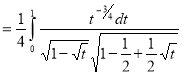 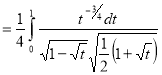 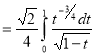 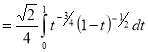 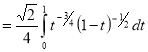 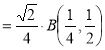 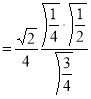  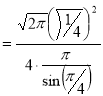  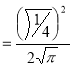
Example(5): Show that 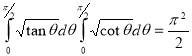 Solution : 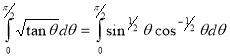 =   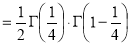 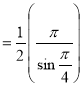  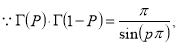 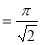 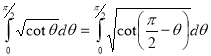 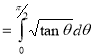 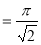  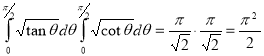 |
Evaluation of integrals
1. 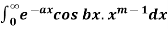
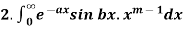
 by using beta and gamma functions-
by using beta and gamma functions-
Evaluation of the first interal-

Evaluation of the second integral-
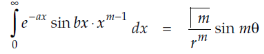
Example: Prove that-
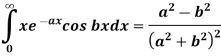
Where a>0.
Sol.
We know that-
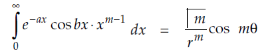
Put m – 1 = 1 or m = 2
We get-
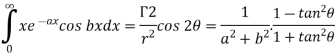
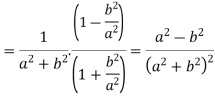
Hence proved
Key takeaways-
And
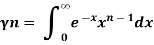
2. 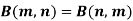
3. 
4. 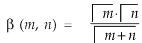
References:
- C.Ray Wylie, Louis C.Barrett : "Advanced Engineering Mathematics", 6th Edition, 2. McGraw-Hill Book Co., New York, 1995.
- James Stewart : “Calculus -Early Transcendentals”, Cengage Learning India Private Ltd., 2017.
- B.V.Ramana: "Higher Engineering Mathematics" 11th Edition, Tata McGraw-Hill, 2010.
- Srimanta Pal & Subobh C Bhunia: “Engineering Mathematics”, Oxford University Press, 3rd Reprint, 2016.
- Gupta C.B., Singh S.R. And Mukesh Kumar: “Engineering Mathematics for Semester I & II”, Mc-Graw Hill Education (India) Pvt.Ltd., 2015.