Unit – 3

Series solution of differential equation

3.1 Power series method

Working Rule

Step 1 Let 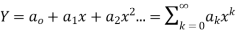be the solution of the given differential equation.

Step 2: Find 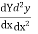etc.

Step 3: Substitute the expression of in the given differential equation.

Step 4: Calculate coefficient of various powers of x by equating coefficients to zero.

Step 5: Substitute the values of in the differential equation to get the required series solution.

Example. Solve in series the equation

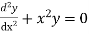
Ans. 

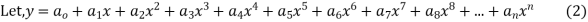
Since x=0 is the ordinary point of the equation (1)

Then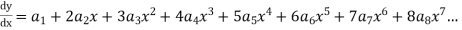

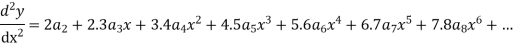
Substituting in (1) we get

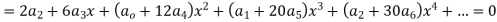
Equating to zero the coefficient of the various powers of x we obtain

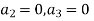
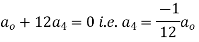
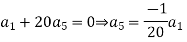
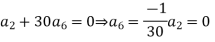
Substituting these values in (2) we get

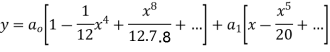
Solve.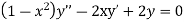

Ans. Let,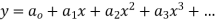

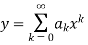
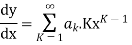
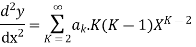
Substituting the value of 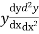  in the given equation we get

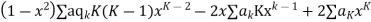
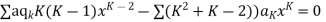
Where the first summation extends over all values of K from 2 to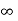

And the second from K =

Now equating the coefficient of 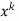equal to zero we have

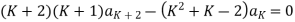
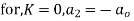
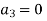
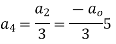
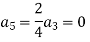
For K =4

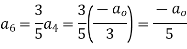
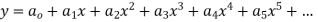
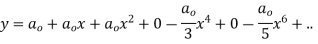
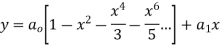
Solve.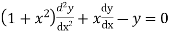

Ans. Let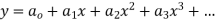

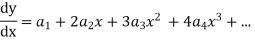
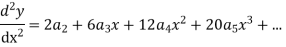
Substituting for 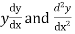in the given differential equation

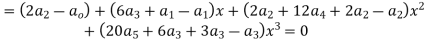
Equating the coefficients of various powers of x to zero we get

3.2 Legendre’s equation

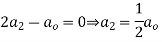
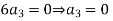
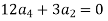
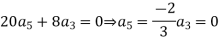
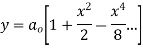
Legendre’s equation is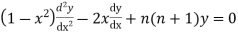

And

Prove that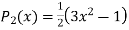

Ans. We know that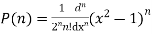

Put n=2

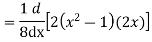
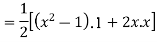
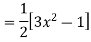
Prove that .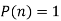

Ans. We know

+

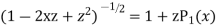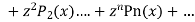
Put x = 1 both sides we get

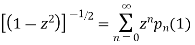
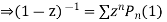
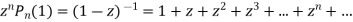
Equating the coefficient of 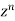on both sides we get

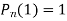
Prove that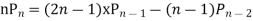

Ans. We know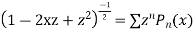

Differentiating with respect to z we get

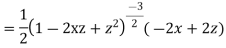
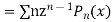
Multiplying both sides by 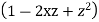we get

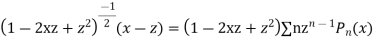
Equating the coefficient of 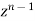from both sides we get

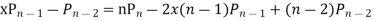
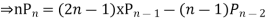
Solve. Statement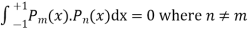

Proof. Let 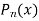is a solution of

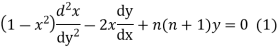
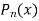is the solution of

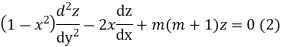
Multiplying (1) by z and (2) by y and subtracting we get

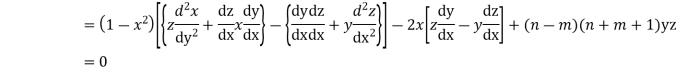
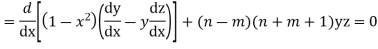
Now integrative -1 to 1 we get

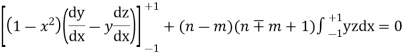
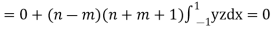
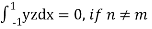
Now we have to prove that

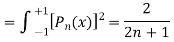
We know that,

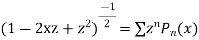
Squaring both sides we get

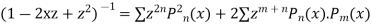
Integrating both sides between -1 to +1 we get

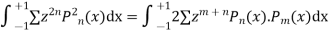
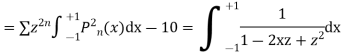
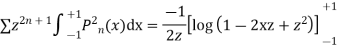
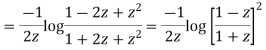
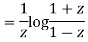
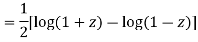
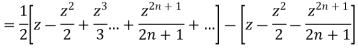
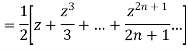
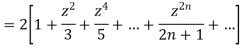
on both sides we get

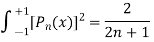
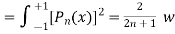here n = m

Prove that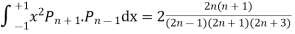

Ans. The Recurrence formula is

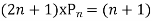Pn+1+nPn-1

Replacing n by (n+1) and (n-1) we have

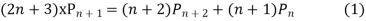
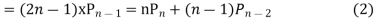
Multiplying (1) and (2) and integrating in the limits -1 to 1 we get

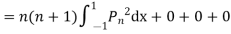(By orthogonality property)

3.3 Legendre’s polynomial

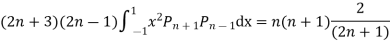
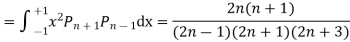
Rodrigues' Formula: The Legendre Polynomials 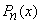 can be expressed by Rodrigues' formula

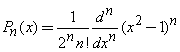 where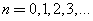 

Generating Function: The generating function of a Legendre Polynomial is

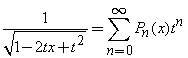
Orthogonality: Legendre Polynomials 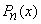, , 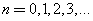form a complete orthogonal set on the interval 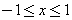. It can be shown that

By using this orthogonality, a piecewise continuous function  in 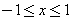 can be expressed in terms of Legendre Polynomials:

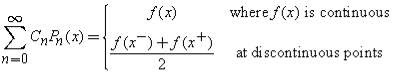
Where:

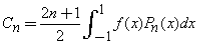
This orthogonal series expansion is also known as a Fourier-Legendre Series expansion or a Generalized Fourier Series expansion.

Even/Odd Functions: Whether a Legendre Polynomial is an even or odd function depends on its degree .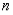

Based on ,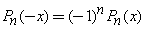

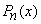•  is an even function when  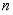is even.

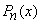•  is an odd function when  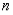is odd.

In addition, from,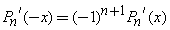

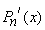•  is an even function when  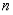is odd.

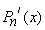•  is an odd function when  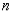is even.

Recurrence Relation: A Legendre Polynomial at one point can be expressed by neighboring Legendre Polynomials at the same point.

• 

• 

• 

• 

• 

3.4 Bessel’s equation

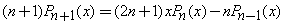
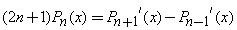
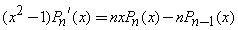
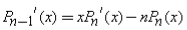
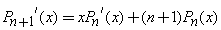
The Bessel equation is

3.5 Bessel’s function

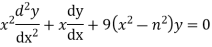
The Bessel equation is

Bessel function of first kind

Bessel function of second kind

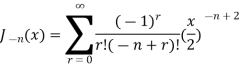
Recurrence Formula

1)     xJn'=nJn-xJn+1

2)    

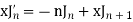
3)    

4)    

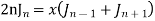
5)    

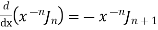
6)    

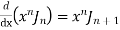
Prove that (1)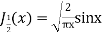

Ans. We know

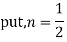
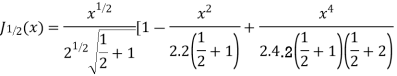
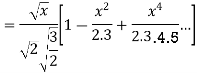
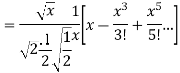
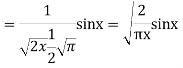
(b) Prove that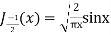

Ans. We know that

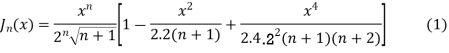
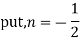
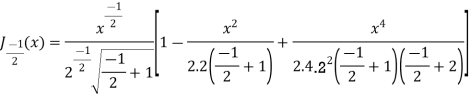
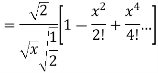
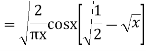
(3) Prove that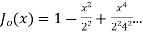

Ans. We know that

Jn(x)=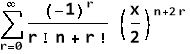

If n = 0

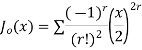
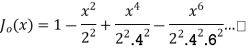
If n = 1

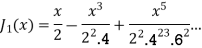
Note General solution of Bessel Equation

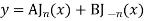
Text Book:

1) Calculus: Gorakh Prasad

2) Advance Engineering Mathematics – E. Kreyszig, John Wiley & Sons Inc.