Unit - 2
Thermodynamic Potentials
Thermodynamic Variables
The thermodynamic state of a system can be determined by quantities like temperature (T), Volume (V), pressure (P), internal energy (U), entropy (S) etc. These quantities are known as thermodynamic variables, or parameters of the system.
Any change in one of the variables results in a change in the thermodynamic state of the system.
Thermodynamic variables are the quantities like pressure, volume and temperature, which help us to study the behaviour of a thermodynamic system. There are some other thermodynamic variables such as entropy, internal energy etc. but these thermodynamic variables can be expressed in terms of pressure, volume and temperature. These properties undergo change when the system
Passes from one state to another i.e., thermodynamic variables are path dependent. These variables are also known as macroscopic co-ordinates.
Intensive Thermodynamic Variables
An intensive property is a bulk property, meaning that it is a physical property of a system that does not depends on the size or the amount of the material in the system.
Examples of intensive properties include temperature, pressure, density, viscosity, hardness, refractive index, specific volume, emf, etc.
Extensive Thermodynamic Variables
An extensive property is a physical quantity whose magnitude is additive for the system. The value of such an additive property is proportional to the size of the system or to the quantity of matter in the system.
Examples of the extensive property is length, area, volume, mass, internal energy, entropy, electric charge, heat capacity, magnetisation etc.
The ratio of two extensive properties of the same object or system may be an intensive property.
For example, the ratio of an object's mass and volume, which are two extensive properties, is density (M/V), or specific volume (V/M), which is an intensive property.
Key Takeaways
- The thermodynamic state of a system can be determined by quantities like temperature (T), Volume (V), pressure (P), internal energy (U), entropy (S) etc. These quantities are known as thermodynamic variables.
- An intensive property is a bulk property, meaning that it is a physical property of a system that does not depends on the size or the amount of the material in the system.
- An extensive property is a physical quantity whose magnitude is additive for the system.
Thermodynamic Potentials
The internal energy (U) of a thermodynamic system is a state function which simply means that a system undergoes the same change in U when moved from one equilibrium state to another, irrespective of the path followed. However, this path independence of internal energy makes it very useful. Although it is not a uniquely useful quantity there could be some other combinations of the state variables (i.e., pressure p, volume V, temperature T, and entropy S) which when added with the internal energy function may result quantities having dimensions of energy. Also, this preserves the nature of path independence. These new state functions are very useful and termed as thermodynamic potentials.
Whereas, all such combinations may not be helpful in the study of a thermodynamic system but the combinations like U + PV, U — TS and U + PV — TS are found to have significant role and are named as enthalpy (H), Helmholtz function (F), and Gibb’s function (G) respectively.
All the thermodynamic properties of a system can be calculated by differentiating these functions
A thermodynamic potential is a scalar quantity used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886.
Four common thermodynamic potentials are:
- Internal energy (U) is the capacity to do work plus the capacity to release heat.
- Gibb’s energy (G) is the capacity to do non-mechanical work.
- Enthalpy (H) is the capacity to do non-mechanical work plus the capacity to release heat.
- Helmholtz free energy (F) is the capacity to do mechanical plus non-mechanical work.
Thermodynamic potentials are of practical importance in studying the equilibrium conditions of a thermodynamic system.
The thermodynamic state of a homogeneous system may be represented by means of certain selected variables such as pressure P, volume V, temperature T and entropy S.
Out of these four variables any two may vary independently and when known enable the others to be determined.
Thus, there are only two independent variables and the others may be considered as their functions.
Taking two of the four state variables P.V.T and S at a time, there are six variable pairs. i.e. (P V), (P, T), (P, S), (V, T), (V, S), (T, S) corresponding to each pair. We can write a thermodynamic relation.
There exists certain relation between these thermodynamic variables.
The first and second law of thermodynamics provide two relations given as
DQ = dU + PdV
And
DQ = TdS
Therefore.
TdS = dU + PdV
Or
DU = TdS - PdV
This expresses the change in internal energy of the system in terms of four thermodynamic variables. However, for a complete knowledge of the system_ certain other
Or, dU = TdS — PdV
This expresses the change in internal energy of the system in terms of four thermodynamic variables. However, for a complete knowledge of the system, certain other relations are required and for this purpose we introduce some functions of the variables P, V, T and S which are known as thermodynamic potentials or the thermodynamic functions.
Internal Energy (U)
The internal energy U of the system is a thermodynamic variable which characterises the system. This is also called the intrinsic energy or internal energy.
When the system passes from one state to another, the change in the internal energy is independent of the path followed in between the two states.
The internal energy of a system is defined as the equation
DU = dQ - dW
Where dW = PdV is the external work done while
DQ = TdS
DU = TdS — PdV ….... (1)
(a) For an adiabatic process
DQ = 0
DU = - PdV
i.e., the work done by the system in an adiabatic process is at the expense of its internal energy.
(b) For an isochoric adiabatic process
DV = 0 and dQ = 0
DU = 0 or U= constant
The internal energy of system remains constant in an isochoric adiabatic process.
Enthalpy (H)
Enthalpy is an extensive thermodynamical property and is of particular significance. It is defined as
H=U+PV
For an infinitesimal reversible change, we get
DH = dU + PdV + VdP
DH = TdS — PdV + PdV + VdP
DH = TdS + VdP .......... (2)
(a) For reversible isobaric process
DP = 0
DH = TdS = dQ
Thus, for an isobaric process, the change in enthalpy is equal to the beat absorbed.
(b) For an isobaric adiabatic process
DP =0 and dQ= 0
DH =0
H = Constant enthalpy remains constant in a resemble isobaric adiabatic process.
Helmholtz Free Energy (F)
The Helmholtz free energy is also called as 'Helmholtz function' or 'Thermodynamic Potential at constant volume' and it is defined by the equation
F = U - TS
Since U. T and S are perfect differentials, F is also a perfect differential.
When a system undergoes an infinitesimal reversible change from an initial equilibrium state to a final equilibrium state.
The Helmholtz free energy changes by an amount given by differentiating the above relation as
DF = dU - TdS - SdT
But as shown in the earlier case
DU = TdS — PdV
So
DF= (TdS — PdV) — TdS — SdT
DF = —SdT — PdV ........... (3)
This equation gives the change in Helmholtz free energy during an infinitesimal reversible process.
(a) For Reversible isothermal process
DT = 0
DF = —PdV
Or
PdV = -dF
Thus, the work done dime in a reversible isothermal process is equal to the decrease in Helmholtz free energy.
(b) For isothermal isochoric process
DT = 0 and dV = 0
DF = 0
F = Constant
The Helmholtz free energy remains constant during isothermal isochoric process.
Gibbs' Free Energy (G)
This is also known as Gibb's Function' or 'Thermodynamic Potential at constant pressure'. It is defined as
G = H — TS
For an infinitesimal reversible process
DG = dH — TdS — SdT
But dH = TdS + VdP
So
DG = VdP — SdT ……. (4)
(a) For an isothermal isobaric process
DT = 0 and dP = 0
DG = 0 or G = Constant
Thus, Gibbs free energy remains constant in an isothermal isobaric process.
Key Takeaways
- A thermodynamic potential is a scalar quantity used to represent the thermodynamic state of a system.
- The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886.
- Internal energy (U) is the capacity to do work plus the capacity to release heat. Gibb’s energy (G) is the capacity to do non-mechanical work.
- Enthalpy (H) is the capacity to do non-mechanical work plus the capacity to release heat.
- Helmholtz free energy (F) is the capacity to do mechanical plus non-mechanical work.
2.3.1 Surface Films and Variation of Surface Tension with Temperature
If such a film is stretched, its volume remaining constant, the energy equation for this case is
(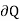 )v =du -2
)v =du -2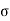 dA,
dA,
For the work done by the film is -2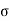 dA, where a is the surface tension and dA the increase in area of the film.
dA, where a is the surface tension and dA the increase in area of the film.
The usual term pdv on the right has disappeared since the total volume remains constant. Hence corresponding to p and dv we have in this case -2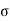 and dA respectively. Therefore
and dA respectively. Therefore
(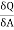 )T,v = -2T (
)T,v = -2T ( )v,A
)v,A
And for a finite change
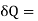 -2T (
-2T (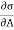 )v dA
)v dA
For a liquid the surface tension decreases with temperature, therefore 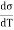 is negative and his case is
is negative and his case is 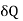 is positive. Hence an amount of heat must be supplied to the film when it is its temperature may remain constant. In a temperature will fall by an amount
is positive. Hence an amount of heat must be supplied to the film when it is its temperature may remain constant. In a temperature will fall by an amount
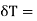
 (
(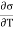 )v dA
)v dA
CA is the heat capacity of the film.
2.3.2 Magnetic Work
According to Kittel, “A great deal of unnecessary confusion exists as to how to write the First Law of Thermodynamics for a magnetic system”.
For a paramagnetic crystal in a uniform magnetic field B, with total magnetic dipole moment M, there are two forms for the work done when B and M change.
The form δWms applies when the mutual field energy is included in the system, the form δWs when it is not.
They assume that the volume of the crystal does not change when a change in the magnetic field is imposed; with this assumption, no work is done on the lattice alone.
Consequently, the work forms are valid whether or not the lattice is included in the system. The form δWs = −MdB thus applies to the systems Ps (whose internal energy is just the potential energy of the spins in the field) and Psl (which includes the lattice energy as well).
The form δWms = BdM applies to the systems Pms and Pmsl, which add the mutual field energy to the first two systems.
Now Ps and Pms, to which the lattice is external, are bona fide thermodynamic systems, exchanging heat and work with their environment, possessing an internal energy, entropy, and temperature, and obeying the first and second laws of thermodynamics.
The systems are in no way “unphysical” or “unrealistic.” Indeed, the thermal physics of Ps has well-known applications.
For example, adiabatic cooling is explained in some elementary texts by consideration just of Ps, with only passing reference to the lattice. And the statistical mechanics of Ps takes a particularly simple form, so it appears frequently in developments of elementary concepts.
Notice that we do not assume that the spins are adiabatically separated from the lattice, only that any heat transfer to the lattice is considered a transfer of energy out of the system.
Notwithstanding, the relaxation time between nuclear spins and the lattice is so slow that these spin systems may be considered isolated from the lattice.
The realization that such spin systems are thermodynamic systems in their own right underlies the modern recognition of the existence of negative absolute temperatures.
Both δWms and δWs lead to correct forms of the first law
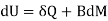
Applies to the systems Pms and Pmsl, while
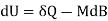
Applies to Ps and Psl
Since δQ = T dS for reversible changes, we have
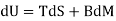
For Pms and Pmsl, and
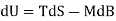
For Ps and Psl.
Key Takeaways
- For a liquid the surface tension decreases with temperature.
- For a paramagnetic crystal in a uniform magnetic field B, with total magnetic dipole moment M, there are two forms for the work done when B and M change.
In 1926, Debye and Giauque showed theoretically that the temperatures considerably below 1K could be obtained by the process known as adiabatic demagnetisation of a paramagnetic salt.
We know that those substances for which the magnetic susceptibility x is small, but positive are paramagnetic in nature.
Experimental Method
The apparatus used is shown in Figure below. The paramagnetic specimen (salt) is suspended in a vessel A, which is surrounded by liquid helium. Liquid helium taken in Dewar flask D, is boiled under reduced pressure. It is surrounded by Dewar flask D2 containing liquid hydrogen. The salt is in contact with the helium gas. A magnetic field of the order of 30,000 Gauss is applied.
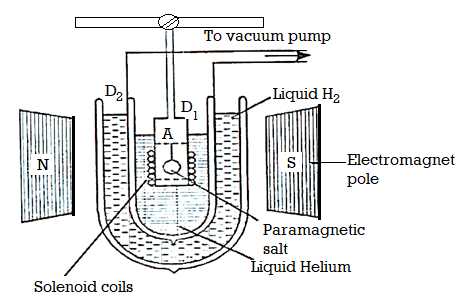
Figure 1: Cooling due to adiabatic demagnetization
When the magnetic field is switched on, the specimen (salt) is magnetised. The heat due to magnetisation is removed by first introducing hydrogen gas into A and then pumping it off with high vacuum pump, so that the specimen is thermally isolated.
In the meantime, the specimen picks up the temperature. Now the magnetic field is switched off. Adiabatic demagnetisation of the specimen takes place and its temperature falls. The temperature of the specimen is determined by fitting a coaxial solenoid coil around the tube A and measuring the self-inductance and hence susceptibility of the substance at the beginning and the end of experiment. Then temperature T is called by Curie law χ = C/T.
The entire phenomena is also called Magneto-Caloric effect.
Haas, in 1994, was able to produce temperature upto 0.002K using a double sulphate of potassium and aluminium. Klerk, Stenland and Goiter used powder mixed crystal of chromium alum and aluminium alum and went down to a temperature of 0.0014K
Theory
When a paramagnetic material is placed in a magnetising field II, its elementary magnetic dipoles align parallel to the direction of the field. The magnetic moment thus produced per unit volume is called the intensity of magnetisation (I). According to Curie's law, this intensity of magnetisation is directly proportional to the magnetising field H and inversely proportional to temperature T of the paramagnetic substance. Thus
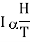
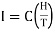 …... (1)
…... (1)
Where C is a constant, known as Curie constant.
If V is the volume of I mole of the substance, then intensity of magnetisation of I mole of paramagnetic substance
M = IV …... (2)
Substituting for I from equation (1), we get
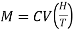 …... (3)
…... (3)
In the experiment, let 1 mole of paramagnetic substance is placed in magnetising field H. Then its thermodynamic behaviour can be expressed in terms of thermodynamic variables P, V, T and S. In thermodynamic system, an increase in pressure P results in decrease in volume V, analogously in our case any increase in H results in an increase in M. Hence replacing P by —H and V by M in Maxwell's third thermodynamic relation
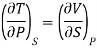
We have
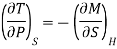
Or
 …... (4)
…... (4)
Multiply numerator or denominator by T, we get
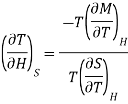
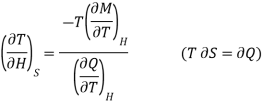
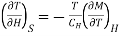 …... (5)
…... (5)
Where
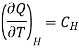
Specific heat of the substance at constant the magnetic field H.
Since the process is carried out adiabatically. So S is constant. For Infinitesimal change
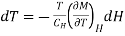 …... (6)
…... (6)
Thus, when field is changing from H1 to H2, Corresponding temperature change is given as
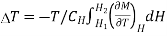 …... (7)
…... (7)
Differentiating equation with respect to T at constant H, we get
 …... (8)
…... (8)
Substituting in equation (7)
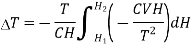
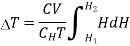
 …... (9)
…... (9)
If the magnetic field is reduced from H1 = H to H2 = 0, then the change in temperature will be
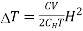 …... (10)
…... (10)
The following conclusions can be drawn from the equation (10)
(i) The temperature of paramagnetic solid decreases as the magnetising field is reduced (shown by negative sign of  )
)
(ii) Greater is the initial field H and lower is the initial temperature T, greater is the temperature fall 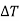 .
.
(iii) It is to be noted that here CV is the Curie constant per mole. If 1 gm of paramagnetic substance is taken, then CV would stand for Curie constant per gm.
Key Takeaways
- In 1926, Debye and Giauque showed theoretically that the temperatures considerably below 1K could be obtained by the process known as adiabatic demagnetisation of a paramagnetic salt.
- If the magnetic field is reduced from H1 = H to H2 = 0, then the change in temperature will be
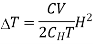
Phase Transitions
A phase of the matter may be defined as a thermodynamic system of which all the physical properties (such as density. Refractive index. Magnetization and chemical composition etc.) are essentially uniform.
In simple words, a region of matter that is chemically uniform, physically distinct, and mechanically separable may be thought of a phase.
We are familiar with different forms of water i.e., ice (solid). Water (liquid), and vapour/steam (gas). These three forms are three different phases of the water.
In general, the distinct phases may be described as different states of such as gas, liquid and solid.
Apart from these three, some other states or phases of mater are also known namely plasma or Bose—Einstein condensate.
The uniformity in the physical properties of certain phase is due to the uniform interactions such as attractive forces between the constituents forming the phase under some fixed external thermodynamic conditions i.e., temperature, pressure etc.
However, the change in the external conditions may result into the change in the kind and/or strength of the interactions which in turn gives some different phase. The ice (solid phase) When heated up to its melting point changes into water (liquid phase) and water when further heated up to its boiling point changes into the gaseous phase. This phenomenon of transition of the matter from one to another phase is termed as phase transition.
During a phase transition of a given medium certain properties of the medium change and these are common occurrences observed in nature.
The studies about the phase transitions of the materials are very important as they provide proper understanding of the material's behaviour and their applications in thermodynamics.
Classification of phase transitions
Most of the natural phase transitions occur at constant temperature and latent heat is required for such transitions to take place. On the other hand, some phase changes such as transition of material from ferromagnetic to paramagnetic phase at its Curie temperature, transition of a compound from super-conducting state to non-superconducting state, transition from liquid He I to liquid He II etc., do not require latent heat. Depending upon whether latent heat is involved or not during a phase transition, P. Ehrenfest proposed a classification of phase transitions and categorized them as first and second order phase transitions.
First Order Phase Transition
First order phase transition can be defined as that one in which the Gibbs function with respect to pressure and temperature change discontinuously at the transition point.
In other words, the first derivatives of Gibb's function are discontinuous. However, the value of the Gibbs function is the same in both the phases at equilibrium.
In these processes, there is transference of heat and hence there is change in entropy and volume. These changes are represented graphically in Figure.
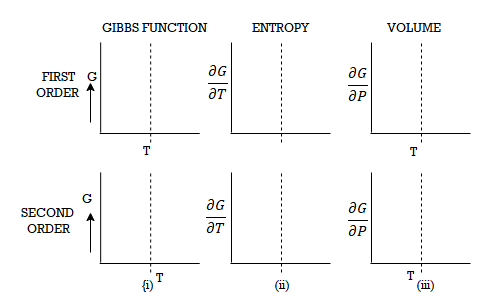
Figure 2: Phase Transition
Second Order Phase Transition
According to the definition proposed by Ehrenfest, the phase transitions in which the second derivatives of Gibbs function are discontinuous whereas the Gibbs function and its first derivatives are continuous at phase transition are termed as second order phase transitions.
Second order phase transitions can be defined as the phenomenon that takes place with no change in entropy and volume at constant temperature and pressure.
It has been found in case of transition from liquid helium Ito liquid helium II, that there is no transfer of heat and no change in volume. Such transitions are called second order phase transitions. These changes are represented graphically in Figure.
Key Takeaways
- A phase of the matter may be defined as a thermodynamic system of which all the physical properties (such as density. Refractive index. Magnetization and chemical composition etc.) are essentially uniform.
- Ehrenfest proposed a classification of phase transitions and categorized them as first and second order phase transitions.
Clapeyron in 1834, and Clausius in 1850, deduced an important equation which describes conditions governing changes of state, such as melting of solids and boiling of liquids. This is known as the Clausius-Clapeyron equation' or the 'first latent heat equation'.
Let ABCD and EFGH represent the two isothermals at infinitely close temperatures T and (T+dT) respectively.
From Figure, the parts AB and EF correspond to the liquid state of the substance. At B and F, substance is purely in the liquid state.
Along BC and FG, the change of state is in progress and the liquid and vapour states coexist in equilibrium.
At C and G, the substance is purely in vapour state.
From C to D and G to H the substance is in the vapour state.
Let P and (P+dP) be the saturated vapour pressures of the liquid at temperatures T and (T+dT) respectively and let V1 and V2 be the volumes of the substance at F and G respectively.
Let us draw two adiabatics from F and G meeting the lower isothermal at M and N respectively.
Let us suppose that 1 gm of the substance is taken round a reversible Carrot cycle FGNMF, allowing it to expand isothermally along FG, adiabatically along GN, compressing it isothermally along NM and adiabatically along ME.
The amount of heat Q1 absorbed along FG is equal to the latent heat of vaporisation (L+dL) at temperature (T+dT), as substance changes completely from liquid state at F to the vapour state at G.
Also, the quantity of heat Q2 rejected along the isothermal compression NM, is L, the latent heat at temperature T. Here latent heat is supposed to vary with temperature.
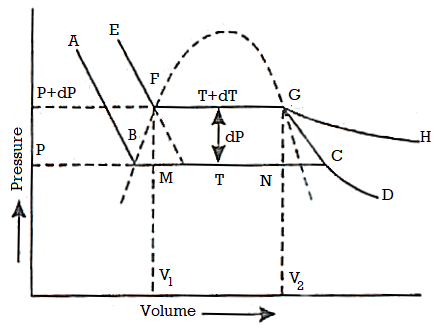
Figure 3: P-V Curve
Using Carnot Cycle result
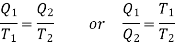
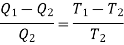
We have 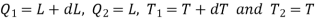
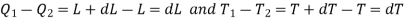
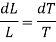
 ……. (1)
……. (1)
The amount of heat converted into work during cycle FGMNF is
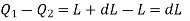
But the work done during the Carrot cycle is given by the area FGMNF, which may be treated as a parallelogram.
Hence,
DL (in work unit) = Area FGMNF
= FG x perpendicular distance between FG and NM
= (V2 — V1) x dP
Where V2 and V1 are the specific volumes in vapour and liquid state respectively, dP expresses the difference of pressure between FG and NM.
Substituting this value of dL in equation (1)
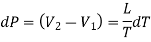
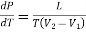 ……. (2)
……. (2)
Eq. (2) is called the Clapeyron's latent heat equation and holds for both the changes of state, i.e., from liquid to vapour and solid to liquid.
Applications
- Effect of change of pressure on the melting point.
When a solid is converted into a liquid, there is change in volume
(i) If V2 is greater than V1, then dP/dT is a positive quantity. It means that the rate of change pressure with respect to temperature is positive. In such cases, the melting point of the substance will increase with increase in pressure and vice versa
(ii) If V2 is less than V1, then dP/dT is a negative quantity. It means that the rate of change of pressure with respect to temperature is negative. In such cases, the melting point of the substance will decrease with increase in pressure and vice versa. In the case of melting of ice, the volume of water formed is less than the volume of ice taken. Hence V2 is less than V1.
Therefore, the melting point of ice decreases with increases in pressure. Hence ice will melt at a temperature lower than zero degree centigrade at a pressure higher than the normal pressure.
2. Effect of change of pressure on the boiling point
When a liquid is converted into a gaseous state, the volume V, of the gas is always greater than the corresponding volume Vi of the liquid i.e., V2 > V1. Therefore, dP/dT is a positive quantity.
With increase in pressure, the boiling point of a substance increases and vice versa. The liquid will boil at a lower temperature under reduced pressure. In the case of water, the boiling point increases with increase in pressure and vice versa.
Water bolls at 100 °C only at 76 cm of Hg pressure. In the laboratories, while preparing steam, the boiling point is less than 100 c because the atmospheric pressure is less than 76 cm of Hg. In pressure cookers, the liquid boils at higher temperature because the pressure inside is more than the atmospheric pressure.
Clausius Equation
The second latent heat equation, or the equation of Clausius, gives the variation of latent heat of a substance with temperature and connects it with the specific heat of the substance in the two states.
Let C1 denote the specific heat of liquid in contact with its vapours and C2 the specific heat of saturated vapours in contact with its liquid. Let us consider that 1 gm of the substance is taken round the cycle BFGCB. The quantity of heat absorbed by the substance in passing from B to F, when its temperature rises by dT is C1dT. In passing along FG, when the substance changes from liquid to vapour at constant temperature T+dT, it absorbs a quantity of heat L+dL.
In passing from G to C, the temperature of the substance (vapours) falls by dT and hence it gives out a quantity of heat C2dT, while in passing along CB, when it condenses from vapour to liquid at constant temperature T, gives out a quantity of heat L.
Hence the net amount of heat absorbed during the cycle is
= C1dT + L + dL — C2dT — L
= (C1 — C2)dT + dL.
This must be equal to the work done which is equal to the area of the cycle or the area FGNMF in the limiting case and hence from equation (2)
DP (V2 — V1) =  dT
dT
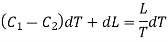
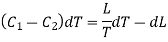
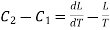 ……. (3)
……. (3)
This is second latent heat or Clausius equation.
Ehrenfest equations
Ehrenfest equations (named after Paul Ehrenfest) are equations which describe changes in specific heat capacity and derivatives of specific volume in second-order phase transitions.
The Clausius–Clapeyron relation does not make sense for second-order phase transitions, as both specific entropy and specific volume do not change in second-order phase transitions.
Ehrenfest equations are the consequence of continuity of specific entropy and specific volume, which are first derivatives of specific Gibbs free energy – in second-order phase transitions. If one considers specific entropy as a function of temperature and pressure, then its differential is
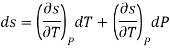
As
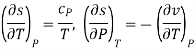
Then the differential of specific entropy also is
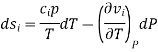
Where and are the two phases which transit one into other. Due to continuity of specific entropy, the following holds in second-order phase transitions ds1=ds2
So,
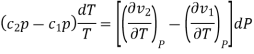
Therefore, the first Ehrenfest equation is

The second Ehrenfest equation is got in a like manner, but specific entropy is considered as a function of temperature and specific volume
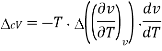
The third Ehrenfest equation is got in a like manner, but specific entropy is considered as a function of v and P
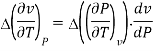
Continuity of specific volume as a function of and gives the fourth Ehrenfest equation
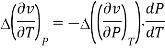
Derivatives of Gibbs free energy are not always finite. Transitions between different magnetic states of metals can't be described by Ehrenfest equations.
Example: If the boiling point of benzene at 1 atm pressure is 353 K. Calculate the approximate value of the vapour pressure of benzene at 303 K.
Solution:
Using Clapeyron's equation
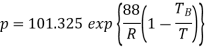
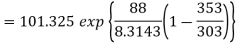
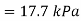
Key Takeaways
- Clapeyron in 1834, and Clausius in 1850, deduced an important equation which describes conditions governing changes of state, such as melting of solids and boiling of liquids. This is known as the Clausius-Clapeyron equation' or the 'first latent heat equation'.
- Ehrenfest equations (named after Paul Ehrenfest) are equations which describe changes in specific heat capacity and derivatives of specific volume in second-order phase transitions.
- The Clausius–Clapeyron relation does not make sense for second-order phase transitions, as both specific entropy and specific volume do not change in second-order phase transitions.
The state of a homogenous system is completely determined if we know its mass and any two of the thermodynamic variables P, V, T, U and S. Thus, the internal energy U of a system is completely determined if V and T are given i.e., U is a function of the two variables V and T. Among the five thermodynamic variables certain relations exist, of which four are important and known as 'Maxwell's thermodynamic relations'.
Let us deduce these relations
From the First Law of Thermodynamics
DQ = dU +dW
DQ = dU +PdV
DU = dQ - PdV ……… (1)
And from second law of thermodynamics
DQ =TdS ……… (2)
Substitute the (2) in (1)
DU = TdS - PdV ……… (3)
Let U, S and V be the function of two independent variable x and y. Where x and y may be any two variables out of S, T, P and V.
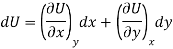

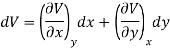
Substitute the value of dU, dS and dV in eq (3)
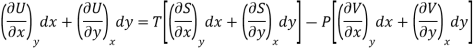
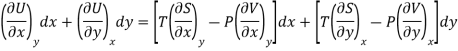
Equating the coefficient of x and y on both sides
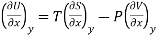 ……… (4)
……… (4)
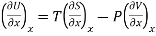 ……… (5)
……… (5)
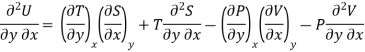
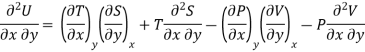
As dU is perfect differential
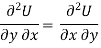
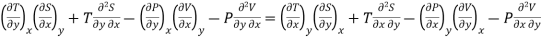 ……… (6)
……… (6)
Since dS and dT is also perfect differential.
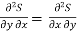 and
and 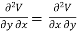
Thus eq (6) becomes
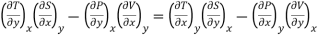 ……… (7)
……… (7)
This is the general expression for Maxwell's thermodynamic relations. In place of the independent variables x and y, any two of the four variables S, T, P and V can be substituted so that there may be one mechanical variable (P or V) and one thermal variable (S or T). Thus, there may be four sets of possible substitutions (S, V), (T, V), (S, P) and (T, P), providing the four Maxwell's thermodynamic relations.
Maxwell's First Relation
Substitute x = S and y = V in equation (7), so that
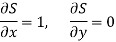

Putting these values in equation (7), we get
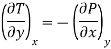
But 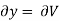 (as y=V) and
(as y=V) and 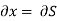 (as x=S)
(as x=S)
Hence
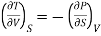 ……… (8)
……… (8)
This is Maxwell's first thermodynamic relation.
Maxwell's Second Relation
Substitute x = T and y = V in equation (7), so that

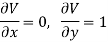
Putting these values in equation (7), we get
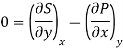
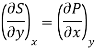
But 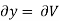 (as y=V) and
(as y=V) and 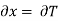 (as x=T)
(as x=T)
Hence
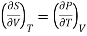 ……… (9)
……… (9)
This is Maxwell's second thermodynamic relation.
Maxwell's Third Relation
Substitute x = S and y = P in equation (7), so that
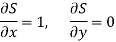
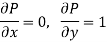
Putting these values in equation (7), we get
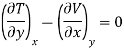

But  (as y=P) and
(as y=P) and 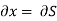 (as x=S)
(as x=S)
Hence
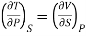 ……… (10)
……… (10)
This is Maxwell's Third thermodynamic relation.
Maxwell's Fourth Relation
Substitute x = T and y = P in equation (7), so that

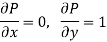
Putting these values in equation (7), we get
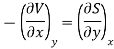
But 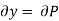 (as y=P) and
(as y=P) and 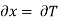 (as x=T)
(as x=T)
Hence
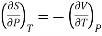 ……… (11)
……… (11)
This is Maxwell's Fourth thermodynamic relation.
Relations (8), (9), (10), (11) are four important thermodynamic relation and any of these relations based on its suitability can be used to solve a particular problem.
Example: Calculate under what pressure water would boil at 1500C if the change in specific Volume when 1 gm of water is converted into steam is 1676 c.c. Given latent heat of vaporization of steam =540 cal per gm.
Solution:
From Maxwell’s Second equation
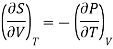


Here 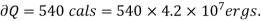
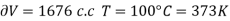
Hence 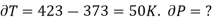
On substituting the value
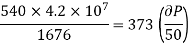
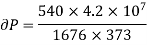
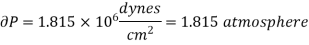
Hence required pressure at which water boil at 1500C = 1+ 1.815 = 2.815atm
Key Takeaways
- The state of a homogenous system is completely determined if we know its mass and any two of the thermodynamic variables P, V, T, U and S.
- Thus, the internal energy U of a system is completely determined if V and T are given i.e., U is a function of the two variables V and T.
1. Clausius Clapeyron Equation
Maxwell's second thermodynamic relation is written as
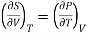 ………. (1)
………. (1)
Multiplying both sides by T, we have
 ………. (2)
………. (2)
But, T S =
S = 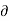 Q, (from second law of thermodynamics). Hence
Q, (from second law of thermodynamics). Hence
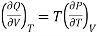 ………. (3)
………. (3)
Here represents the quantity of heat absorbed or liberated per unit change in volume at constant temperature. This mean that at constant temperature the heat absorbed or liberated bring out simply a change in the volume of the substance. Therefore, this quantity of heat absorbed or liberated at constant temperature must be the latent heat and the change in volume must be due to a change of state. Considering a unit mass of substance, let L be the latent heat when the substance changes its volume from V1 to V2 at constant temperature, then
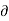 Q =L and
Q =L and 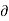 V=V2—V1
V=V2—V1
Substituting these values in the above expression
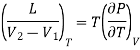
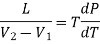
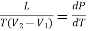 ………. (4)
………. (4)
This is the Clausius-Clapeyron latent heat equation.
2. Relation between CP and CV
(i) Specific heat at constant pressure and volume
 ………. (5)
………. (5)
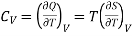 ………. (6)
………. (6)
If the entropy S is regarded as a function T and V and since dS is perfect differential.
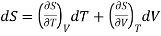 ………. (7)
………. (7)
Differentiating w.r.t T at constant P
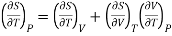 ………. (8)
………. (8)
Multiplying with T both sides, we have
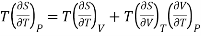 ………. (9)
………. (9)
From Maxwell Second relation
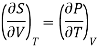
So that
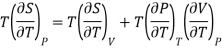
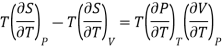
From (1) and (2)
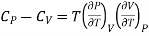 ………. (10)
………. (10)
(ii) But P is a function of T and V and since dP is perfect differential.
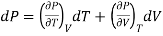 ………. (11)
………. (11)
If the change take place at constant P, then dP =0

Differentiating w.r.t T at constant P
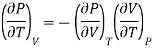
Substituting in (10)
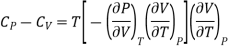
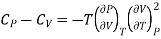 ………. (12)
………. (12)
But we know that coefficient of elasticity is given as
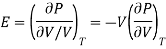
And coefficient of Volume expansion is given as
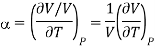
Then eq (12) become
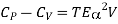 ………. (13)
………. (13)
(iii) For perfect gas
PV =RT
Differentiating w.r.t T at constant P and at constant V, we have
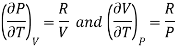
Hence eq (10) becomes
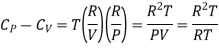
Cp - Cv = R ………. (14)
(iv) For Van der- wall’s equation, the equation of gas
 ………. (15)
………. (15)
Where a and b are constants
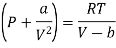
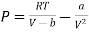 ………. (16)
………. (16)
Differentiating w.r.t T at constant V, we have
 ………. (17)
………. (17)
Differentiating eq (17) w.r.t T at constant P, we have

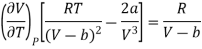
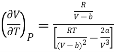 ………. (18)
………. (18)
Substituting the equation (17) and (18) in eq (10), we get
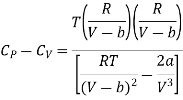
Divide by RT / (V-b)2 numerator and denominator in R.H.S equation of the above equation
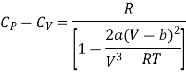
Neglecting b in comparison to V
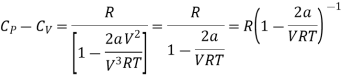
Expanding binomially and neglecting the higher order terms, we obtain
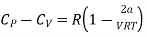 ……. (19)
……. (19)
3. TdS Equations
(i) Let us take entropy S of thermodynamic system as a function of Temperature T and volume V
S = S (T, V)
Taking its perfect differential
 ……. (1)
……. (1)
Multiply both side by T
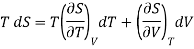
 ……. (2)
……. (2)
Also from Maxwell’s IInd relation
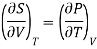
Making these substitutions in equation (2), we get
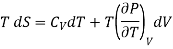
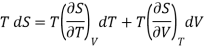
 . (3)
. (3)
(ii) Let us take entropy S of thermodynamic system as a function of Temperature T and volume P
S = S (T, P)
Taking its perfect differential

Multiply both side by T
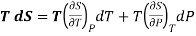 ……. (4)
……. (4)
But
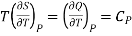 ……. (5)
……. (5)
Also from Maxwell’s IVrd relation
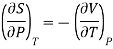
Substitutions in equation (4), we get
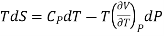 ……. (6)
……. (6)
4. Joule-Kelvin coefficient for Ideal and Van der Waal Gases
When a gas under a constant pressure is made to pass through an insulated porous-plug to a region of lower constant pressure, it suffers a change in temperature. This is called the 'Joule -Thomson or Joule-Kelvin effect'.
The process is called the Throttling process. The change in temperature is proportional to the pressure-difference between the two sides of the plug. At ordinary temperature, all gases, expect hydrogen and helium, show a cooling effect while hydrogen and helium show a heating effect.
Let us consider 1 mole of gas. Let Pl and V1 be its pressure and volume before passing and P2 and V2 the pressure and volume after passing through the porous plug.
The net external work done by the gas in passing through the plug = P2V2 - P1V1
Since there is no heat-exchange between the gas and its surroundings this work must come from the internal energy of the gas.
Thus, if U1 and U2 be the internal energies of the gas before and after passing through the plug, we have from the first law of thermodynamics
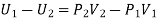
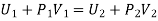
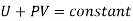
The quantity U+PV which remains constant through Throttling process is called Enthalpy of the gas. So, we can write
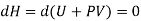
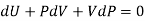
But dU = TdS –PdV and dQ =TdS from thermodynamics law.
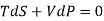 ……….. (1)
……….. (1)
Let us assume the entropy S is regarded as function of temperature and pressure and also dS is perfect differential.
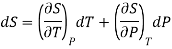
Substituting this value in (1)
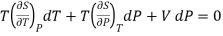 ……….. (2)
……….. (2)
But dQ =TdS,
Therefore

Where Cp is specific heat at constant pressure.
Maxwell’s fourth equation
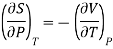
Therefore equation (2) becomes
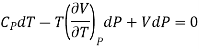
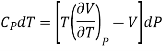
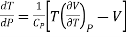 ……….. (3)
……….. (3)
Enthalpy remains constant through Throttling process, we can write dP/dT as (dP/dT)H is called Joule Thomson coefficient μ.
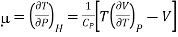 ……….. (4)
……….. (4)
Upon integrating, we get Temperature change for finite drop in pressure from P1 to P2.
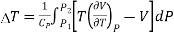 ……….. (5)
……….. (5)
(i) For perfect gas
PV =RT
Differentiating w.r.t T at constant P, we have

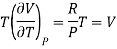
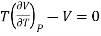 …….. (6)
…….. (6)
Substituting in Joule Thomson coefficient we get
μ =0
Thus, Joule Thomson coefficient for perfect gas is zero.
(ii) For Van der- wall’s equation, the equation of gas
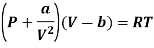
Where a and b are constants
Differentiating w.r.t T at constant V, we have
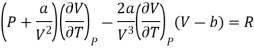
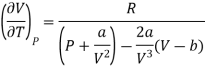
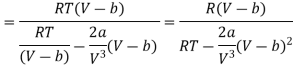
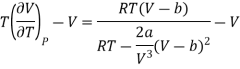
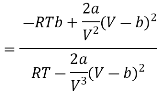
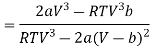
Since, a and b are very small quantities, we replace 2aV (V — b)2 by 2aV3 in the numerator and ignore 2a (V — b)2 in comparison with RTV3 in the denominator. Then, we get
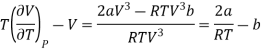
Substituting this result in equations (3) and (4), we get
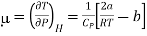 ….... (8)
….... (8)
And 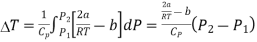 ….... (9)
….... (9)
The pressure is lower on the emergent side of the porous plug (P2 < P1). Hence,
We may write as
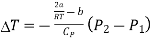 ….... (10)
….... (10)
This expression shows the Joule-Thomson effect for real gas.
5. Energy Equations
DQ = dU + PdV
And
DQ = TdS
Therefore.
TdS = dU + PdV
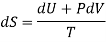
Making substitution in Maxwell’s 2nd Relation
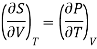
We get
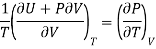
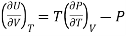 ……. (7)
……. (7)
This is called First Energy equation. This shows variation of internal energy with Volume
Again
DU = TdS - PdV
Dividing by dP, we get
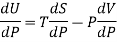
Where U, V, S are regarded as function of temperature T and pressure P.
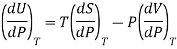
From Maxwell’s third equation
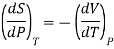
Therefore
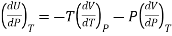 ……. (8)
……. (8)
This is called Second Energy equation. This shows variation of internal energy with Pressure.
For Ideal Gas
For 1 mole of ideal gas
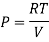

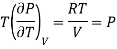
Putting in equation (7)

The internal energy of ideal gas is independent of Volume at constant temperature.
This called Joule’s law.
For Van Der Wall’s Gas
For 1 mole of Van Der Wall’s Gas
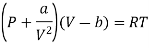
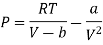

Putting in equation (7)
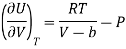
Putting the value of RT/V-b from Van Der Wall’s Gas equation.
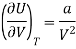
Which is positive and the internal energy of actual gas does depend on Volume at constant temperature.
(6) Change of Temperature during Adiabatic Process
(i) From first thermodynamic-relation
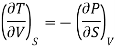
On multiplying and dividing by T the right-hand side, we get
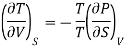
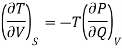
Since an increase-in the amount of heat at constant volume always results in an increase of pressure; the term [ P/
P/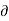 Q]V is positive.
Q]V is positive.
Hence the term [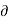 T/
T/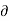 V]S should be negative that is i.e., the temperature should decrease with an increase in volume under condition of constant entropy (adiabatic process).
V]S should be negative that is i.e., the temperature should decrease with an increase in volume under condition of constant entropy (adiabatic process).
In other words, an adiabatic expansion must result in a fall of temperature
In a similar way, third thermodynamic relation

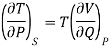
Since an increase in the quantity of heat at constant pressure always results in an increase in volume the term [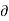 V/
V/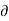 Q]P is positive. Hence the term. [
Q]P is positive. Hence the term. [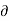 T/
T/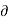 P]S is must also, be positive i.e., the temperature must increase with an increase in pressure under conditions of constant entropy.
P]S is must also, be positive i.e., the temperature must increase with an increase in pressure under conditions of constant entropy.
In other words, an adiabatic compression always results in an increase of temperature.
Example: For a copper disc at 300K, Isothermal compressibility K =7.78 x 10-12N/m2, Specific heat at constant pressure Cp =24.5J/mol K, Volume is 7.06cm3/mol and coefficient of expansion 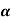 = 50.4 x 10-6 K-1
= 50.4 x 10-6 K-1
Solution:
We know
Cp –Cv =TE 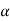 2V
2V
And 
So that 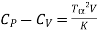
Here 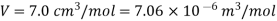
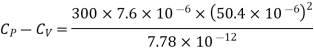
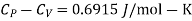
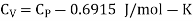
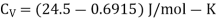
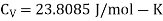
Key Takeaways
- Relation between Cp and Cv
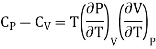
- An adiabatic compression always results in an increase of temperature.
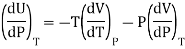
- This is called Second Energy equation. This shows variation of internal energy with Pressure.
- Joule Thomson coefficient for perfect gas is zero.
- The quantity U+PV which remains constant through Throttling process is called Enthalpy of the gas.
References:
1. Theory and experiments on thermal Physics, P.K.Chakrabarty (New central book agency limited)-2017
2. Thermodynamics, Kinetic Theory and Statistical Thermodynamics- Sears and Salinger (Narosa)-1988
3. A Treatise on Heat- Meghnad Saha and B.N.Srivastava (The Indian Press) Heat, Thermodynamics and Statistical Physics, N.Subrahmanyam and Brij Lal (S.Chand Publishing)-2008
4. Thermal and Statistical Physics M.Das, P.K. Jena, S. Mishra, R.N.Mishra (Shri Krishna Publication)-2009