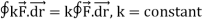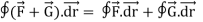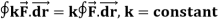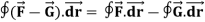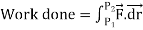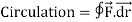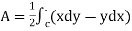Unit - 4
Line integrals
Let- F be vector function defined throughout some region of space and let C be any curve in that region. ṝis the position vector of a point p (x,y,z) on C then the integral ƪ F .dṝ is called the line integral of F taken over
Now, since ṝ =xi+yi+zk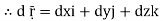
And if F = F1i + F2 j+ F3 k
= F1i + F2 j+ F3 k
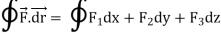
Note-
Q1. Evaluate 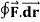 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y= in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
Solution: The curve y= i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
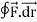 =
= 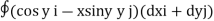
= 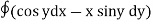
=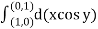 =-1
=-1
Q2. Evaluate 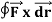 where
where 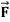 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
Solution: F x dr = 
Put x=t, y=t2, z= t3
Dx=dt, dy=2tdt, dz=3t2dt.
F x dr = 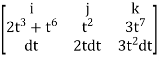
=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=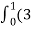 t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=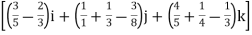
=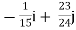 +
+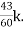
Example 3: Prove that ͞͞͞F = [y2cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞ F (ii) the work done in moving an object in this field from (0, 1, -1) to (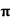 / 2,-1, 2)
/ 2,-1, 2)
 Sol.: (a) The field is conservative if cur͞͞͞͞͞͞F = 0.
Sol.: (a) The field is conservative if cur͞͞͞͞͞͞F = 0.
 Now, curl͞͞͞F =
Now, curl͞͞͞F = 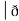 ̷̷
̷̷ X
X  /
/  y
y  /
/ 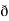 z
z
Y2COS X +Z3 2y sin x-4 3xz2 + 2
; Cur 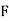 = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k = 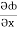 i +
i + 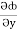 j +
j + 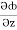 k
k
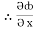 = y2cos x + z3,
= y2cos x + z3, 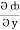 = 2y sin x – 4,
= 2y sin x – 4, 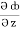 = 3xz2 + 2
= 3xz2 + 2
Now, 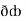 =
= 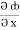 dx +
dx + 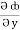 dy +
dy +  dz
dz
= (y2cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =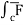 .d ͞r
.d ͞r
= 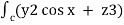 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ](  /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4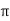 + 15
+ 15
Sums Based on Line Integral
1. Evaluate  where
where  =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
Soln.  = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)
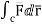 =
=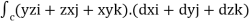
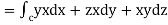
Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
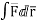 =
=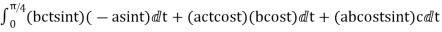
=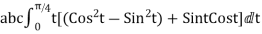
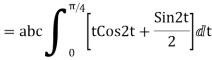
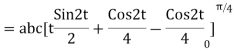
= =
= 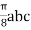
2. Find the circulation of 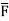 around the curve C where
around the curve C where 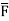 =yi+zj+xk and C is circle
=yi+zj+xk and C is circle 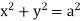 .
.
Sol. Parametric eqn of circle are:
x=a cos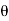
y=a sin
z=0
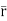 =xi+yj+zk = a cos
=xi+yj+zk = a cos i + b cos
i + b cos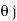 + 0 k
+ 0 k
d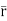 =(-a sin
=(-a sin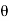 i + a cos
i + a cos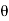 j)d
j)d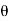
Circulation = =
=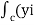 +zj+xk). d
+zj+xk). d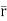
=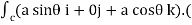 -a sin
-a sin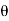 i + a cos
i + a cos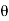 j)d
j)d
=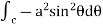 =
= 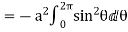


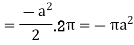
Key takeaways:
Applications of line integral:
- The work done by a force
Let the force  is moving a particle along a curve c from point P1 to P2 as
is moving a particle along a curve c from point P1 to P2 as
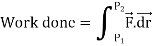
When 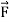 denotes velocity of a fluid, then the circulation of
denotes velocity of a fluid, then the circulation of  around a closed curve c is defined by
around a closed curve c is defined by
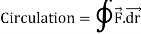
2. Exact differential test
For 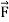 =F1
=F1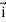 + F2
+ F2 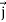 + F3
+ F3 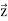 , the necessary and sufficient condition that
, the necessary and sufficient condition that
F1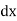 + F2 dy+ F3
+ F2 dy+ F3 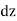 ,
,
Be an exact differential is that F must be conservative.
3. Area of a rectangular region bounded by the curve c

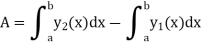
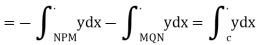
Similarly

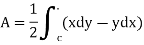
Example: Find the work done in a moving particle in the force field 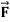 =
=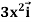 + (2xz – y)
+ (2xz – y)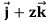 along curve c defined by
along curve c defined by 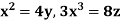 from x = 0 to x = 2.
from x = 0 to x = 2.
Sol:

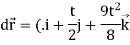
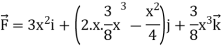
Work done
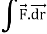
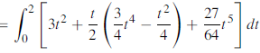
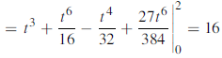
Key takeaways:
Statement- Suppose that C is a smooth curve given by 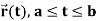 . Also suppose that f is a function whose gradient vector,
. Also suppose that f is a function whose gradient vector,  is continuous on C, then
is continuous on C, then
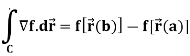
Proof:
The line integral,
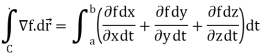
We use the chain rule to simplify the integral,
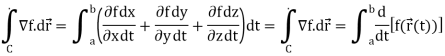
To finish this off, we use the fundamental theorem of calculus for single integral,
We get
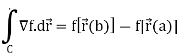
Example: Evaluate 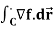 where f(x, y, z) =
where f(x, y, z) = 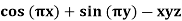 and C is any path that starts at (1, ½, 2) and ends at (2, 1, -1).
and C is any path that starts at (1, ½, 2) and ends at (2, 1, -1).
Sol:
Let  be any path that starts at (1, ½, 2) and ends at (2, 1, -1). Then,
be any path that starts at (1, ½, 2) and ends at (2, 1, -1). Then,
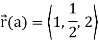
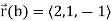
The integral is then,
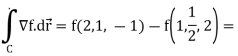
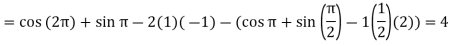
Conservative vector fields-
If  then the field is said to be conservative which means no work is done in displacement from a point a to another point in the field and back to a and the mechanical energy is conserved.
then the field is said to be conservative which means no work is done in displacement from a point a to another point in the field and back to a and the mechanical energy is conserved.
Note- every irrotational field is conservative.
Irrotational fields-
An irrotational field F is characterized by any one of the conditions given below-
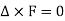
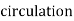
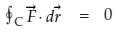 along every closed surface is zero.
along every closed surface is zero.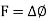 , if the domain is simply connected.
, if the domain is simply connected.
Solenoidal fields-
A solenoidal field F is characterized by any one of the conditions given below-
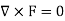
- Flux
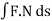 across every closed surface is zero.
across every closed surface is zero. 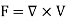
Example: Determine whether F = (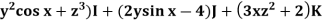 is a conservative vector field.
is a conservative vector field.
Sol:
As we know that F is a conservative vector field when curl F = 0, so that
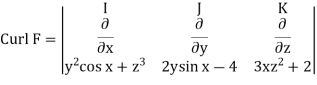
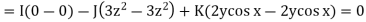
Hence we can say that F is a conservative field.
Independence of path-
If in a conservative field 
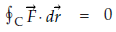
Along any closed curve C.
Which is the condition of the independence of path.
Note- if 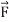 is a conservative vector field then
is a conservative vector field then 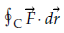 is independent of path.
is independent of path.
Example: Check whether  is independent of path C.
is independent of path C.
Sol:
The line integral of F is independent of path of integration if 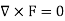
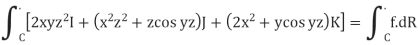
And
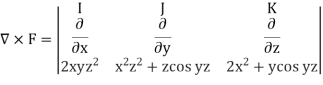
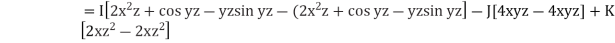
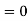
Hence the given integral is independent of path C,
Key takeaways:
- Every irrotational field is conservative.
- If in a conservative field
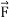

Along any closed curve C.
3. if  is a conservative vector field then
is a conservative vector field then 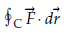 is independent of path.
is independent of path.
Statement- If C be a regular closed curve in the xy-plane and S is the region bounded by C then,
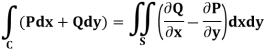
Where P and Q are the continuously differentiable functions inside and on C.
Proof:
Let the equation of the curves AEB and AFB are y = f1(x) and y = f2 (x) respectively.
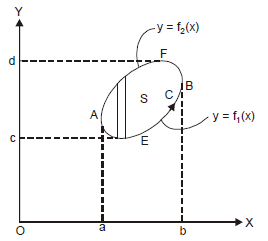
Consider


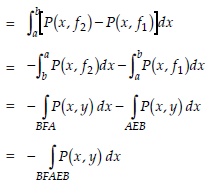
 ….(1)
….(1)
Similarly, let the equations of the curve EAF and EBF be x = f1 (y) and x = f2 (y) respectively, then

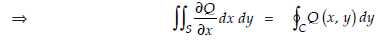 …(2)
…(2)
Adding equation (1) and (2), we obtain
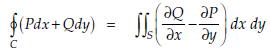
Green’s theorem in vector form-
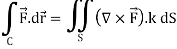
Note- Area of the plane region S bounded by closed curve C cam be calculated as-
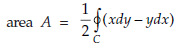
Example-1: Apply Green’s theorem to evaluate 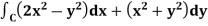 where C is the boundary of the area enclosed by the x-axis and the upper half of circle
where C is the boundary of the area enclosed by the x-axis and the upper half of circle 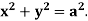
Sol. We know that by Green’s theorem-
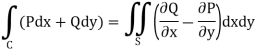
And it it given that-

Now comparing the given integral-
P = 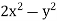 and Q =
and Q = 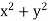
Now-
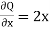 and
and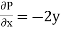
So that by Green’s theorem, we have the following integral-
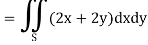
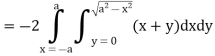
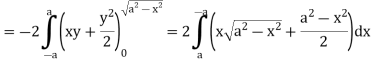
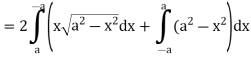
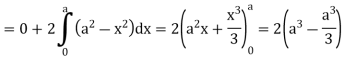
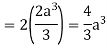
Example-2: Evaluate 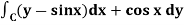 by using Green’s theorem, where C is a triangle formed by
by using Green’s theorem, where C is a triangle formed by 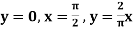
Sol. First we will draw the figure-
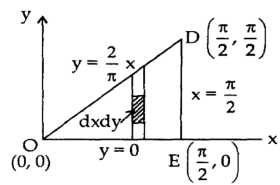
Here the vertices of triangle OED are (0,0), (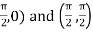
Now by using Green’s theorem-
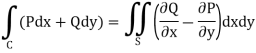
Here P = y – sinx, and Q = cosx
So that-
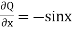 and
and 
Now-

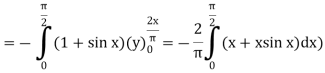
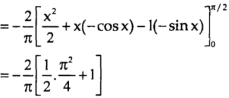
= 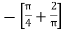
Which is the required answer.
Example-3: Verify green’s theorem in xy-plane for 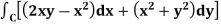 where C is the boundary of the region enclosed by
where C is the boundary of the region enclosed by 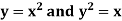
Sol.
On comparing with green’s theorem,
We get-
P = 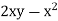 and Q =
and Q = 
 and
and 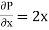
By using Green’s theorem-
 ………….. (1)
………….. (1)
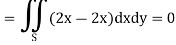
And left hand side= 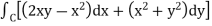
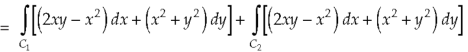 ………….. (2)
………….. (2)
Now,
Along 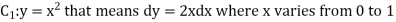
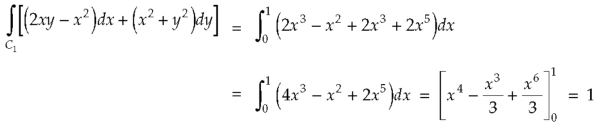
Along 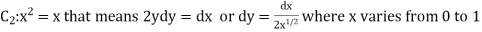
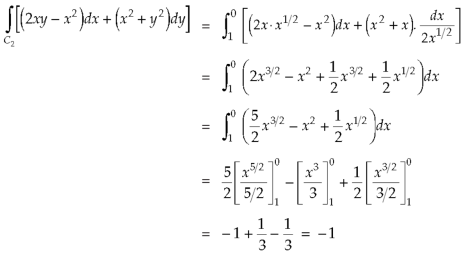
Put these values in (2), we get-
L.H.S. = 1 – 1 = 0
So that the Green’s theorem is verified.
Key takeaways:
1. Green’s theorem in vector form-
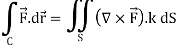
2.
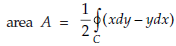
3. 
Definition- An integral which is to be evaluated over a surface is called a surface integral.
Let 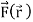 be a continuous vector point function. Let
be a continuous vector point function. Let  =
= 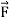 (u, v) be a smooth surface such
(u, v) be a smooth surface such
That 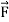 (u, v) possesses continuous first order partial derivatives. Then the normal surface integral
(u, v) possesses continuous first order partial derivatives. Then the normal surface integral
Of 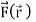 over S is denoted by
over S is denoted by
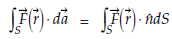
Where d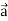 is the vector area of an element dS and
is the vector area of an element dS and 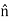 is a unit vector normal to the surface dS.
is a unit vector normal to the surface dS.
Suppose F1, F2, F3 which are the functions of x, y, z be the components of F along the coordinate axes, then surface integral
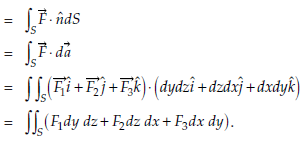
Example: Evaluate
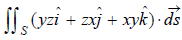
Where S is the surface of the sphere
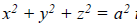 in the first octant.
in the first octant.
Sol:
Here

Vector normal to the surface =
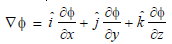
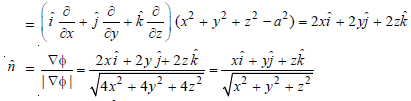
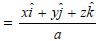
Here
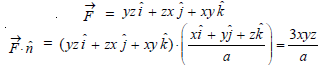
Now
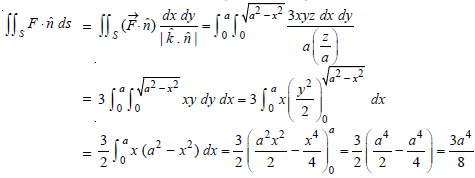
Key takeaways:
- An integral which is to be evaluated over a surface is called a surface integral
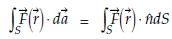
A surface S may be represented by F(x, y, z) = 0.
The parametric representation of surface S is of the form
R(u, v) = x(u, v)I + y(u, v)J + z(u, v)K
And the continuous function 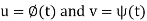 of a real parameter t represent a curve C on this surface S.
of a real parameter t represent a curve C on this surface S.
Example: What will be the parametric representation of the circular cylinder 
The parametric form will be

Where the parameters u and v vary in the rectangle 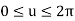 and
and  .
.
Also u = t and v = bt represent a circular helix on the this circular cylinder.
The equation of the circular helix is R = a cost I + a sint J +btK
Definition of smooth surface and piecewise smooth surface:
If S has a unique normal at each of its points whose direction depends continuously on the points of S, then the surface is called a smooth surface.
If S is not smooth but it can be divided into infinitely many smooth portions, then it is called a piecewise smooth function.
Key takeaways:
- A surface S may be represented by F(x, y, z) = 0.
- The parametric representation of surface S is of the form
R(u, v) = x(u, v)I + y(u, v)J + z(u, v)K
Statement-
If 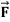 is any continuously differentiable vector point function and S is a surface bounded by a curve C, then-
is any continuously differentiable vector point function and S is a surface bounded by a curve C, then-
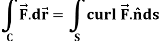
Where 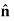 is the unit normal vector at any point of S.
is the unit normal vector at any point of S.
Proof:
Let S is surface such that its projection on the xy, yz and xz planes are regions
Bounded by simple closed curves. Let equation of surface f(x, y, z) = 0, can be written as
z = f1 (x, y)
y = f2 (x, z)
x = f3 (y, z)
Let
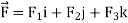
Then we need to show that
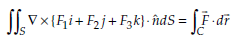
Suppose an integral 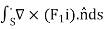 , we have
, we have
 ….(1)
….(1)
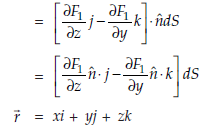 … (2)
… (2)
Also

So that
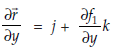
But 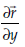 is tangent to the surface S. Hence, it is perpendicular to
is tangent to the surface S. Hence, it is perpendicular to 
So
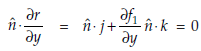
Hence
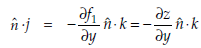
Hence, (ii) becomes
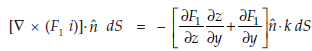 ….(3)
….(3)
But on surface S
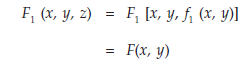 … (4)
… (4)
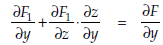 … (5)
… (5)
Hence, (iii) with the help of (v) gives
 ….(6)
….(6)
Where R is projection of S on xy-plane.
Now, by Green’s theorem in plane, we have
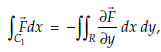
Where C1 is the boundary of R.
As at each point (x, y) of the curve C1 the value of F is same as the value of F1 at each point (x, y, z) on C and dx is same for both curves. Hence, we have
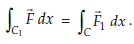
Hence
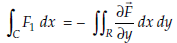 … (7)
… (7)
From eqns. (vi) and (vii), we have
 …(8)
…(8)
Similarly, taking projection on other planes, we have
 …(9)
…(9)
And
 …. (10)
…. (10)
Adding equations (viii), (ix), (x), we get

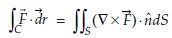
Which is the proof of stoke’s theorem
Example-1: Verify stoke’s theorem when  and surface S is the part of sphere
and surface S is the part of sphere 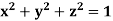 , above the xy-plane.
, above the xy-plane.
Sol.
We know that by stoke’s theorem,
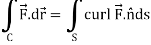
Here C is the unit circle- 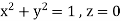

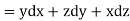
So that-
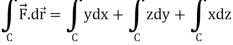
Now again on the unit circle C, z = 0
Dz = 0
Suppose, 
And 
Now
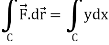
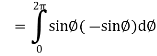
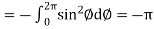 ……………… (1)
……………… (1)
Now-
Curl 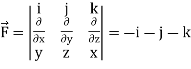
Using spherical polar coordinates-



 ………………… (2)
………………… (2)
From equation (1) and (2), stoke’s theorem is verified.
Example-2: If 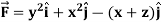 and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate 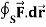 by using Stoke’s theorem.
by using Stoke’s theorem.
Sol. Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 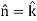
Now,
Curl 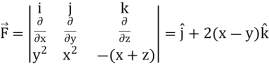
Curl 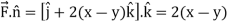
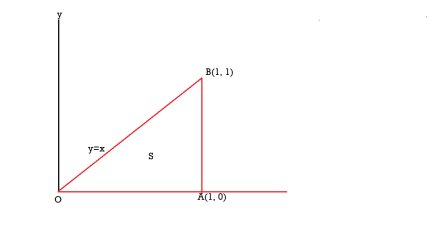
The equation of the line OB is y = x
Now by stoke’s theorem,
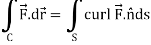
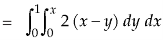
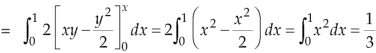
Example-3: Verify Stoke’s theorem for the given function-
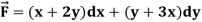
Where C is the unit circle in the xy-plane.
Sol. Suppose-

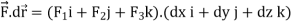
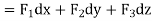
Here 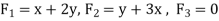
We know that unit circle in xy-plane-
Or
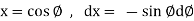
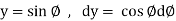
So that,
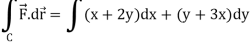
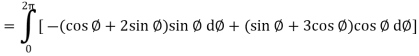
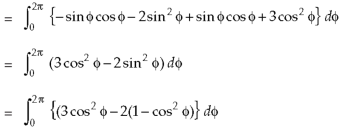
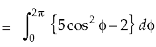
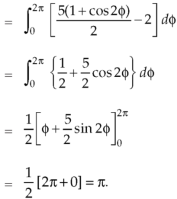
Now
Curl 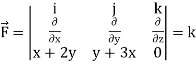
Now,
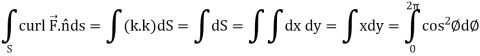
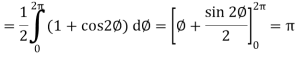
Hence the Stoke’s theorem is verified.
Key takeaways:
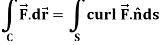
Gauss divergence theorem
Statement:
The surface integral of the normal component of a vector function F taken around a closed surface S is equal to the integral of the divergence of F taken over the volume V enclosed by the surface S.
Mathematically it can be written as-
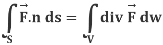
Where  unit vector to the surface S.
unit vector to the surface S.
Note- Divergence theorem is the relationship between surface integral and volume integral.
Proof:
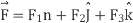
Putting the values of  in the statement of the divergence theorem, we have
in the statement of the divergence theorem, we have
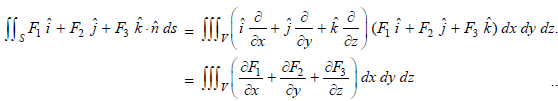 ..(1)
..(1)
We need to prove equation (1),
Let us evaluate, 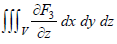
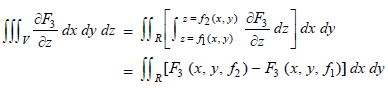 …(2)
…(2)
For the upper part of the surface i.e. S2, we have
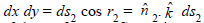
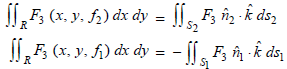
Putting these values in (2), we get
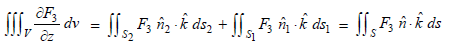 …(3)
…(3)
Similarly, it can be shown that
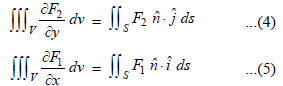
Adding (3), (4) & (5), we have

Hence proved
Example-1: Prove the following by using Gauss divergence theorem-
1. 
2. 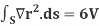
Where S is any closed surface having volume V and 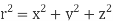
Sol. Here we have by Gauss divergence theorem-

Where V is the volume enclose by the surface S.
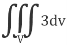
We know that-
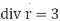
= 3V
2.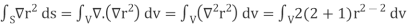
Because 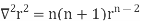
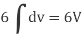
Example – 2 Show that 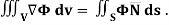
Sol
By divergence theorem,
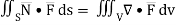 ..…(1)
..…(1)
Comparing this with the given problem let

Hence, by (1)
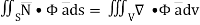 ………….(2)
………….(2)
Now ,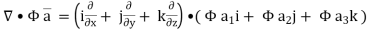
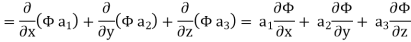
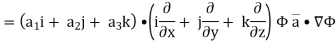
Hence, from (2), We get,
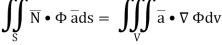
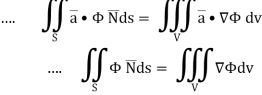
Example Based on Gauss Divergence Theorem
1. Show that

Soln. We have Gauss Divergence Theorem
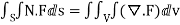
By data, F=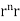

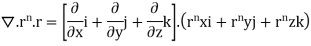
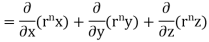
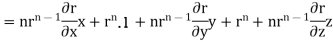

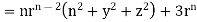
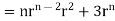
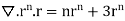
=(n+3)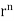

2. Prove that 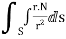 =
=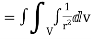
Soln. By Gauss Divergence Theorem,
 =
=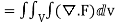
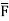 =
=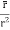 =
=
 .[
.[
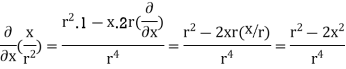
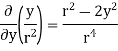
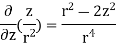
 =
= 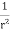
Key takeaways:
References:
1. S C Mallik and S Arora: Mathematical Analysis, New Age International.
2. Publications S Ghorpade, B V Limaye, Multivariable calculus, Springer international edition.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers.
4. Advanced engineering mathematics, by HK Dass.
5. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.