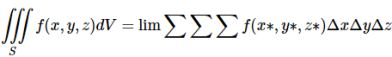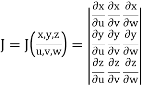Unit - 3
Triple integrals
Triple integral is the generalization of double integral.
First we will understand double integrals before studying triple integrals.
Double integral –
Before studying about multiple integrals, first let’s go through the definition of definition of definite integrals for function of single variable.
As we know, the integral

Where is belongs to the limit a ≤ x ≤ b
This integral can be written as follows-
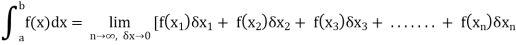
Now suppose we have a function f(x , y) of two variables x and y in two dimensional finite region Rin xy-plane.
Then the double integration over region R can be evaluated by two successive integration
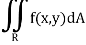
Evaluation of double integrals-
If A is described as 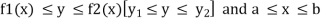
Then,
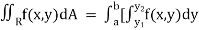 ]dx
]dx
Let do some examples to understand more about double integration-
Example-: Evaluate 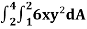 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
Sol. Let, I = 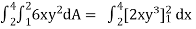
= 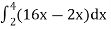
= 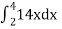
= 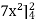
= 84 sq. Unit.
Which is the required area,
Triple integrals
Definition: Let f(x,y,z) be a function which is continuous at every point of the finite region (Volume V) of three dimensional space. Divide the region V into n sub regions of respective volumes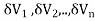 . Let (
. Let (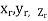 ) be a point in the
) be a point in the 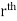 sub region then the sum:
sub region then the sum:
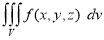 =
= 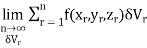
Is called triple integration of f(x, y, z) over the region V provided limit on R.H.S of above Equation exists.
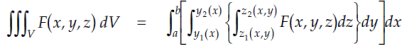
Note-
V is said to be a regular three-dimensional domain if-
(i) Every straight line parallel to z-axis and drawn through an interior point of V cuts the surface S at two points
(ii) Entire V is projected on the xy-plane into a regular two-dimensional domain D.
In triple integration, integration is done first with respect to z (i.e., within the braces) with the substitution of limits for z, the next integration is carried with respect to y (i.e., within the square brackets). This results in an integrand which is a function of x alone which is then integrated with respect to x between a and b.
Example: Evaluate
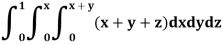
Sol:
First integrating with respect to z, we get

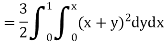
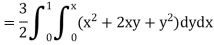
Integrating now with respect to y, we get
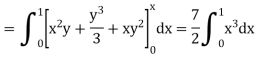
Now we integrate with respect to x
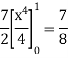
Example: Evaluate
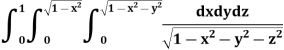
Solution:
Let
I = 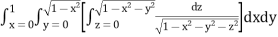
= 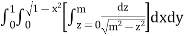
(Assuming m = 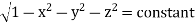 )
)
= 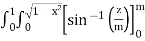 dxdy
dxdy
= 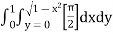
=
= 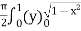 dx
dx
=  dx
dx
= 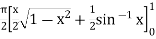
=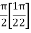
I =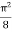
Example: Evaluate 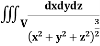 Where V is annulus between the spheres
Where V is annulus between the spheres  and
and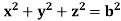 (
( )
)
Solution: It is convenient to transform the triple integral into spherical polar co-ordinate by putting
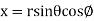 ,
, 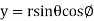 ,
, 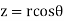
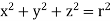 , dxdydz=
, dxdydz=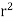 sin
sin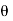 drd
drd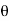 d
d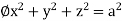 ,
,
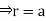 and
and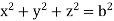
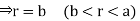
For the positive octant, r varies from r =b to r =a , 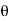 varies from
varies from  and
and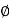 varies from
varies from 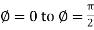
I= 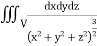
= 8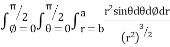
=8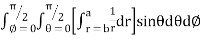
=8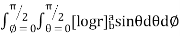
=8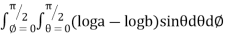
=8 log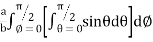
= 8 log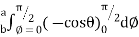
I= 8 log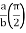
I = 4 log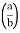
Example-3: Evaluate
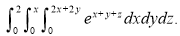
Solution:
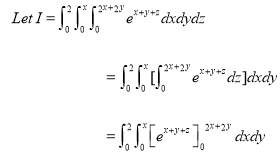

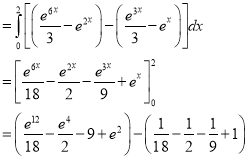
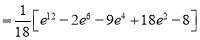
Key takeaways:
- Triple integral is the generalization of double integral.
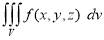 =
= 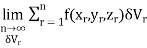
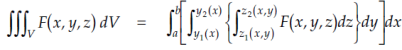
- In triple integration, integration is done first with respect to z (i.e., within the braces) with the substitution of limits for z, the next integration is carried with respect to y (i.e., within the square brackets).
Our definition of a double integral of a real-valued function f(x,y)f(x,y) over a region R in 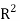 can be extended to define a triple integral of a real-valued function f(x, y, z) over a solid S in
can be extended to define a triple integral of a real-valued function f(x, y, z) over a solid S in 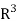 .
.
The solid SS can be enclosed in some rectangular parallelepiped, which is then divided into sub-parallelepipeds. In each sub-parallelepiped inside SS, with sides of lengths Δx, Δy and Δz, pick a point (x∗, y∗, z∗). Then define the triple integral of f(x, y, z) over S, denoted by

And defined as
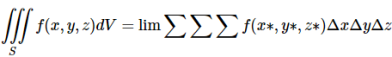
Where the limit is over all divisions of the rectangular parallelepiped enclosing SS into sub parallelepipeds whose largest diagonal is going to 0, and the triple summation is over all the sub parallelepipeds inside SS. It can be shown that this limit does not depend on the choice of the rectangular parallelepiped enclosing SS. The symbol dV is often called the volume element.
In the case where SS is a rectangular parallelepiped 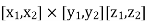 that is, S = (x, y, z) such that
that is, S = (x, y, z) such that 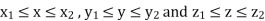
The triple integral is given as,
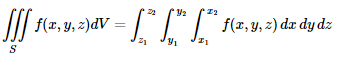
Example: Evaluate
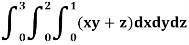
Sol:
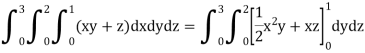
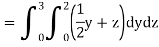

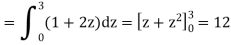
Example: Evaluate
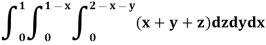
Sol:
We have
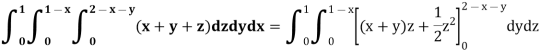
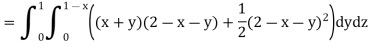
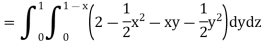
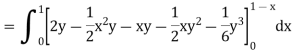
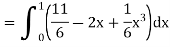
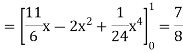
Key takeaways:
In the case where SS is a rectangular parallelepiped  that is, S = (x, y, z) such that
that is, S = (x, y, z) such that 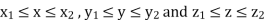
2. The triple integral is given as,

Volume:
The volume of solid is given by
Volume =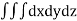
In Spherical polar system
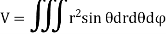
In cylindrical polar system
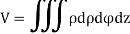
Mass:
If 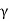 (x, y, z) > 0 is the volume density (mass/unit volume) of distribution of mass over V then the triple integral gives the entire mass contained in V
(x, y, z) > 0 is the volume density (mass/unit volume) of distribution of mass over V then the triple integral gives the entire mass contained in V
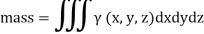
Moment of inertia of a solid:
The moment of inertia of a solid relative to the z-axis is-
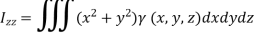
Where 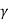 (x, y, z) is the density of the substance. Similarly, moment of inertia of a solid relative to x-axis and y-axis are respectively
(x, y, z) is the density of the substance. Similarly, moment of inertia of a solid relative to x-axis and y-axis are respectively
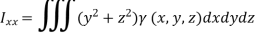
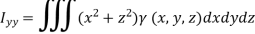
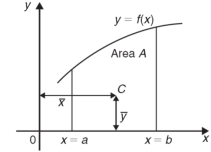
Centre of gravity-
The centre of gravity of a lamina is the point where it balances perfectly which means the lamina’s centre of mass.
If  and
and 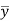 are the coordinates of the centroid C of area A, then-
are the coordinates of the centroid C of area A, then-
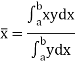
And
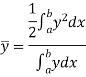
Ex: Find Volume of the tetrahedron bounded by the co-ordinates planes and the plane

Solution:
Volume =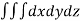 ………. (1)
………. (1)
Put 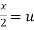 ,
, 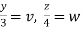
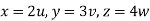
From equation (1) we have
V = 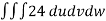
=24
=24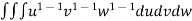 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 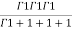
= =
=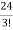 = 4
= 4
Volume = 4
Example: Find the total mass of the region in the cube 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1 with density at any point given by xyz.
Sol:
We know that
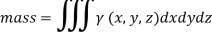
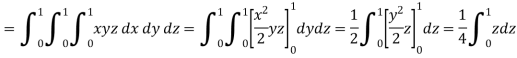

Ex: Find volume common to the cylinders ,
,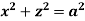 .
.
Solution: For given cylinders,
 ,
, 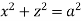 .
.
Z varies from
Z=-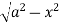 to z =
to z = 
Y varies from
y= -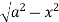 to y =
to y = 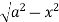
x varies from x= -a to x = a
By symmetry,
Required volume= 8 (volume in the first octant)
=8 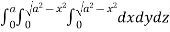
=8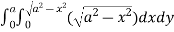
= 8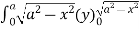 dx
dx
=8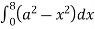
=8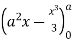
=8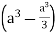
Volume = 16
Ex: Evaluate
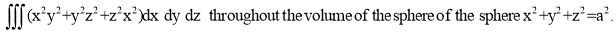
Solution:
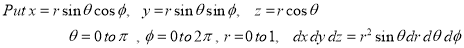
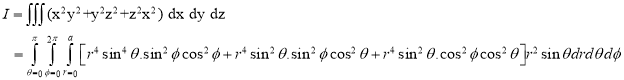
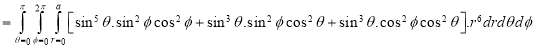
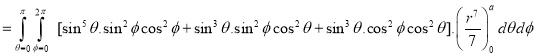
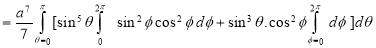
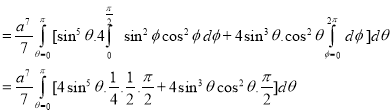
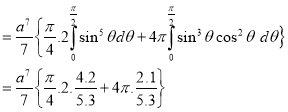
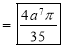
Ex.4: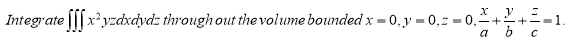
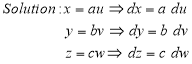
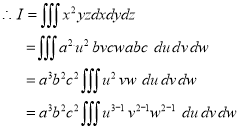
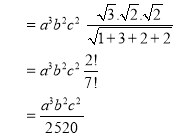
Ex.5: Evaluate
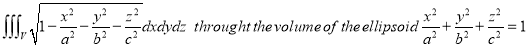
Solution: Put

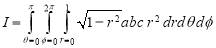
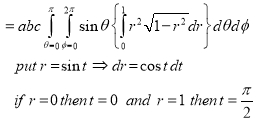

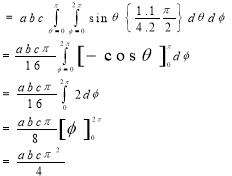
Example: Calculate the volume of the solid bounded by the following surfaces:
z = 0, x^2 + y^2 = 1, x + y + z = 3
Sol:
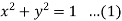
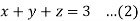
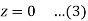
The volume then

On putting x = r cos 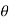 , y = r sin
, y = r sin  , dx dy = r d
, dx dy = r d dr, we get
dr, we get
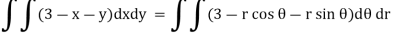
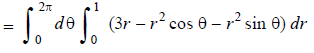
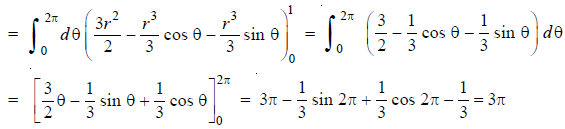
NOTES:
MASS OF A LAMINA: If the surface density ρ of a plane lamina is a function of the position of a point of the lamina, then the mass of an elementary area dA is ρ dA and the total mass of the lamina is 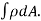
In Cartesian coordinates, if ρ = f(x, y) the mass of lamina, M=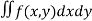
In polar coordinates, if ρ = F(r, Ө) the mass of lamina, M=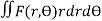
Ex: A lamina is bounded by the curves 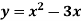 and
and 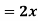 . If the density at any point is
. If the density at any point is 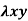 then find mass of lamina.
then find mass of lamina.
Solution:
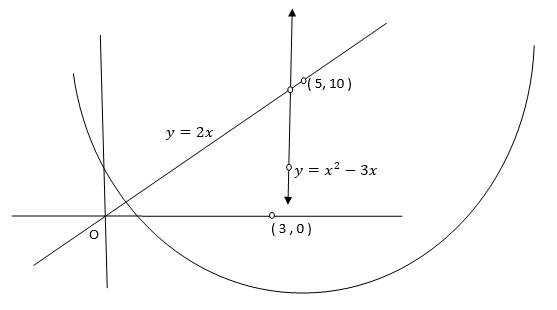

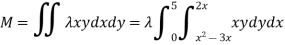

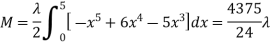
Ex: If the density at any point of a non-uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then find the mass of lamina.
Solution:
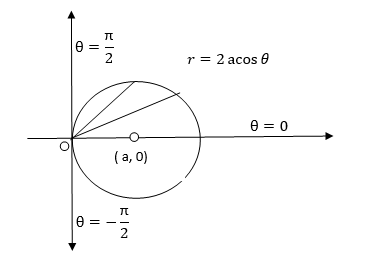
Take the fixed point on the circumference of the circle as origin and diameter through it as x axis. The polar equation of circle 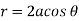
And density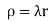 .
.
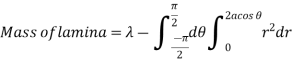
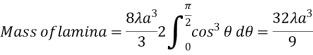
Mean Value:
The mean value of the ordinate y of a function 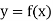 over the range
over the range  to
to 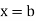 is the limit of mean value of the equidistant ordinates
is the limit of mean value of the equidistant ordinates 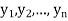 as
as 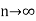
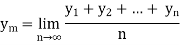
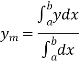
Mean Square values of function 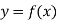 over the range
over the range 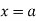 to
to 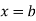 is defined as
is defined as
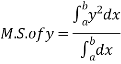
Mean Square values of function 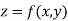
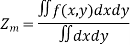
Mean Square values of function 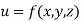
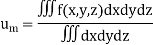
Root Mean Square Value: (R.M.S. Value):
If y is a periodic function of x of period p, the root mean square value of y is the square root of the mean value of 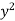 over the range
over the range 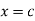 to
to 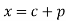 , c is constant.
, c is constant.

Ex: Find mean value and R.M.S. Value of the ordinate of cycloid
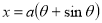 ,
, 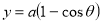 over the range
over the range  to
to 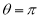 .
.
Sol Let P(x,y) be any point on the cycloid . Its ordinate is y.
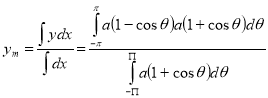

= 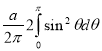
=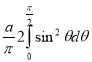
=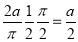
R.M.S. Value=
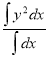
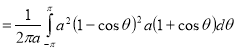
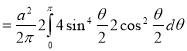
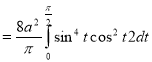
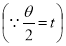
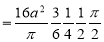
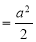
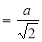
Ex: Find the Mean Value of  Over the positive octant of the
Over the positive octant of the
Ellipsoid 
Sol: M.V.=
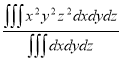
Since
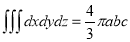
Put
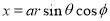
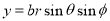
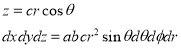
M.V.=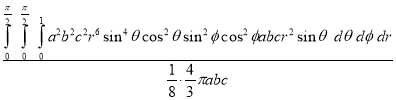

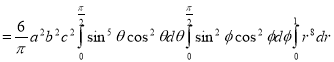
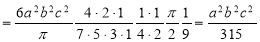
Key takeaways:
- Volume =
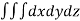
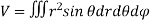
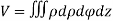
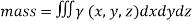
- In Cartesian coordinates, if ρ = f(x, y) the mass of lamina, M=
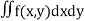
- In polar coordinates, if ρ = F(r, Ө) the mass of lamina, M=

Triple Integral in Cylindrical Coordinates
Cylindrical coordinates 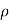 ,
,  , z are particularly useful in problems of solids having axis of symmetry. The transformation of cartesian coordinates x, y, z in terms of cylindrical coordinates
, z are particularly useful in problems of solids having axis of symmetry. The transformation of cartesian coordinates x, y, z in terms of cylindrical coordinates  ,
,  , z are given by x =
, z are given by x =  cos
cos  , y =
, y =  sin
sin 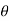 , z = z(
, z = z(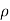 = u,
= u,  = v, z = w) so that the Jacobian is given by
= v, z = w) so that the Jacobian is given by
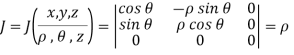
Thus

Triple Integral in Spherical Coordinates
Coordinate transformations from x, y, z to the spherical coordinates 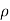 ,
, 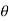 ,
, 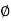 are given by x =
are given by x =  sin
sin 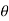 cos
cos 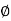 , y =
, y = 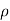 sin
sin 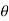 sin
sin 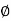 , z =
, z = 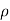 cos
cos 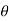 (i.e., u =
(i.e., u = 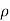 , v = θ , w =
, v = θ , w = 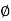 ) so that the Jacobian
) so that the Jacobian
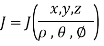
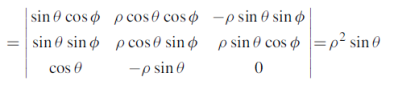
Thus
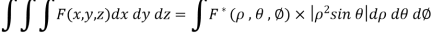
The relations between the cartesian and spherical polar co-ordinates of a point are given by the Relations
x = r sin 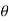 cos
cos 
y = r sin 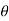 sin
sin 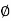
z = r cos 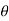
Dx dy dz = | J | dr d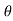 d
d
= r^2 sin 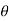 dr d
dr d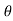 d
d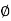
Spherical Polar Coordinates
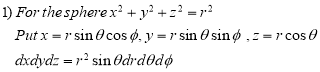
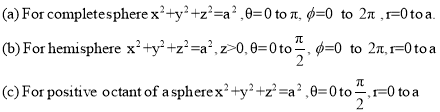

Example: Evaluate the integral-
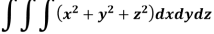
Sol:
First we convert the given integral into spherical polar co-ordinates. By putting
x = r sin  cos
cos 
y = r sin 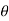 sin
sin 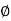
z = r cos 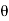
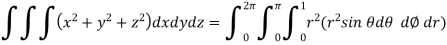
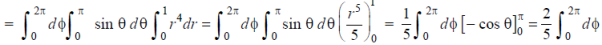

Key takeaways:
1. 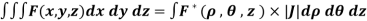
2. 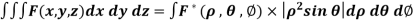
We can solve the double integration by changing independent variables.
Let the double integral is-
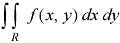
It’s to be changed by the new variables-u and v
The relationship between x, y and u, v are-
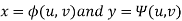
Then the double integration is converted into-
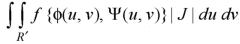
Where-
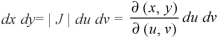
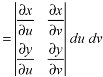
Example-: Evaluate-
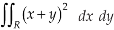
Where-
R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.
Sol.
By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelolgram R reduces to a rectangle 
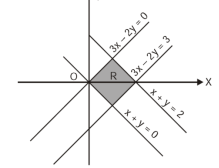

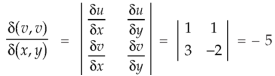
The required Jacobian is-
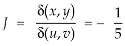
Since u = x + y and u = x + y = 2, here u varies from 0 to 2 while v varies from 0 to 3.
Since-
3x – 2y = v = 0, 3x – 2y = v = 3
Therefore the integral will be in new variables-
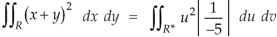
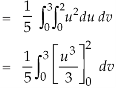
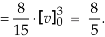
Which is the required answer.
Example: Evaluate 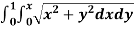 the transformation is x = v and y = uv.
the transformation is x = v and y = uv.
Sol.
Here the region of integration R is the triangle which is bounded by y = 0, x = 1 and y = x
Here put,
X = u and y = uv, we get-
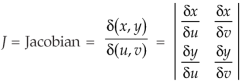
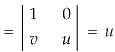
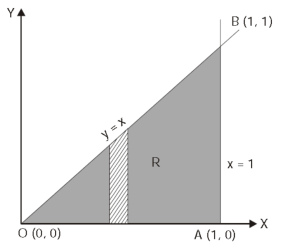
Here x varies from 0 to 1 while y varies from 0 to x.
Since u = x so u varies from 0 to 1
Here, similarly, since  , so that v varies from 0 to 1. Thus-
, so that v varies from 0 to 1. Thus-
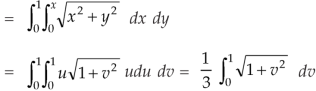
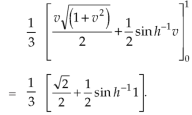
CHANGE OF VARIABLES IN A TRIPLE INTEGRAL:
Let the functions x = f (u, v, w), y = g(u, v, w) and z = h(u, v, w) be the transformations from cartesian coordinates x, y, z to the curvilinear coordinates u, v, w. Then the Jacobian J (x, y, z/ u,v,w) is given by
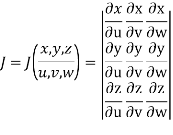
Let F (x, y, z) be a continuous function defined in a domain V in the xyz coordinate system. Then
a triple integral in cartesian coordinates x, y, z can be transformed to a triple integral in the curvilinear coordinates u, v, w as follows:
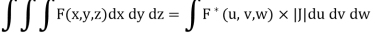
Where 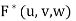 = F (f (u, v, w), g(u, v, w), h(u, v, w)) and V ∗ is the corresponding domain in the curvilinear coordinates u, v, w.
= F (f (u, v, w), g(u, v, w), h(u, v, w)) and V ∗ is the corresponding domain in the curvilinear coordinates u, v, w.
Example: Evaluate-
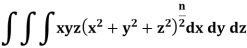
Taken through the positive octant of the sphere 
Sol:
Since the geometry involves sphere, introduce spherical coordinates by x = 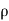 sin
sin 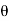 cos
cos 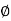 , y =
, y = 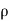 sin
sin 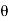 sin
sin 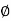 , z =
, z = 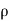 cos
cos 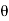 and the jacobian
and the jacobian
We get
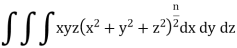
Key takeaways:
2. 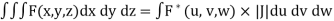
3. The relationship between x, y and u, v are-
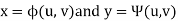
References:
1. S C Mallik and S Arora: Mathematical Analysis, New Age International.
2. Publications S Ghorpade, B V Limaye, Multivariable calculus, Springer international edition.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers.
4. Advanced engineering mathematics, by HK Dass.
5. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.