Unit - 1
Functions of several variables
The function of several variables plays an important role in advanced mathematics.
The area of an ellipse is π ab. It depends on two variables a and b; The total surface area of a rectangular parallelopiped is 2(xy + yz + zx) and it depends on 3 variables x, y, z.
If u = f (x, y, z, t ) then x, y, z, t are known as the independent variables or arguments and u is known as the ‘dependent variable’ or ‘value’ of the function.
Function of two variables-
R denotes the set of real numbers. Let’s D is a collection of pairs of real numbers (x , y), which means D is a subset of R × R.
Then a real valued function of two variables of f is a rule that assign to each point (x, y) in D a unique real number denoted by f(x, y).
The set D is called the domain of f.
The set [ f(x, y): (x, y) belongs to D ], which is the set of values the function f takes, is called range of f.
Here we generally use the letter z to denote the value that a function of two variables takes,
Then we will have,
z = f(x, y)
Here we will call that z is the dependent variable and x and y are independent variables.
Example-1: The area of a rectangular figure whose length is l and breadth is b, given by l × b.
Here independent variables are l and b, but dependent variable is area.
Example-2: the volume of a cylinder is given by πr²h, where r is the radius and h is the height of the cylinder.
In which radius and height are independent variables and volume is dependent.
Example-3: the volume of cuboid is given by l × b× h. Where l, b and h are the length, breadth and height respectively.
L , b and h are independent variable and volume of cuboid is dependent variable.
δ- neighbourhood (Definition)
δ-neighbourhood of a point (a, b) in the xy-plane is a square with centre at (a, b) bounded by the four lines x = a − δ, x = a + δ, y = b − δ, y = b + δ, which means
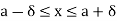
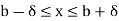
Key takeaways:
- The set [ f(x, y): (x, y) belongs to D ], which is the set of values the function f takes, is called range of f.
- Then a real valued function of two variables of f is a rule that assign to each point (x, y) in D a unique real number denoted by f(x, y).
Limits-
The function f(x,y) is said to tend to limit ‘L’ , as x →a and y→b Iff the limit is dependent on point (x,y) as x →a and y→b
We can write this as,
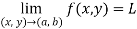
Note-
- If the value of f (x, y) can be made as close to the given finite number L for all those (x, y) in an appropriately chosen
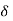 -neighbourhood of (a, b), i.e., for a given
-neighbourhood of (a, b), i.e., for a given 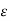 > 0 we can find a
> 0 we can find a 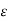 such that
such that

For all (x, y) in the 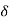 -neighbourhood
-neighbourhood

2. The limit of a function f (x, y) of two variables is said to exist only when the same value we get for the limit along any path in the xy-plane from (x, y) to (a, b) say along x → a and y → b or along y → b and x → a
3. If 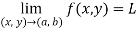 and
and  , then
, then
Example-1: evaluate the 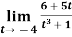
Sol. We can simply find the solution as follows,
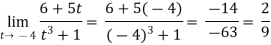
Example-2: evaluate 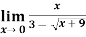
Sol.
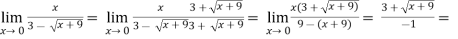 -6.
-6.
Example-3: evaluate 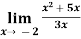
Sol.

Conitinuity
At point (a,b) , a function f(x,y) is said to be continuous if,
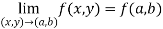
Note-
- A function is said to be continuous in a domain if it is continuous at every point of the domain.
- If f is not continuous at (a, b), it is said to be discontinuous at (a, b).
- If f (x, y) and g(x, y) are continuous at (a, b) then f ± g, f · g and f /g are continuous at (a, b).
Working rule for continuity-
Step-1: f(a,b) should be well defined.
Step-2: 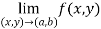 should exist.
should exist.
Step-3: 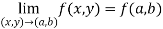
Example-1: Test the continuity of the following function-
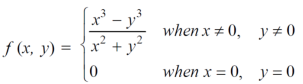
Sol. (1) the function is well defined at (0,0)
(2) check for the second step,


That means the limit exists at (0,0)
Now check step-3:

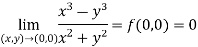
So that the function is continuous at origin.
Example-2: check for the continuity of the following function at origin,
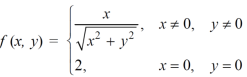
Sol. (1) Here the function is well defined at (0,0)
(2) check for second step-

Limit f is not unique for different values of m
So that the limit does not exists.
Therefore the function is not continuous at origin.
Steps to check for existence of limit-
Step-1: find the value of f(x,y) along x →a and y→b
Step-2: find the value of f(x,y) along x →b and y→a
Note- if the values in step -1 and step-2 are same then we can say that the limits exist otherwise not.
Step-3: if a →0 and b→0 then find the limit along y =mx, if the value does not contain m then limit exist, If it contains m then the limit does not exist.
Note-1- put x = 0 and y = 0 in f, then find f1
2 - Put y = 0 and x = 0 In f then find x2
If f1 and f2 are equal then limit exist otherwise not.
3- put y = mx then find f3
If f1 = f2 ≠f3, limit does not exist.
4- put y = mx² and find f4,
If f1 = f2 = f3 ≠ f4 , limit does not exist
If f1 = f2 = f3 = f4 , limit exist.
Example-1: Evaluate 
Sol . 1. 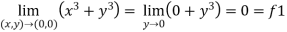
2. 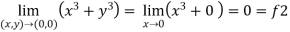
Here f1 = f2
3. Now put y = mx, we get
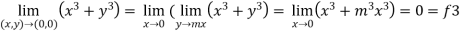
Here f1 = f2 = f3
Now put y = mx²
4. 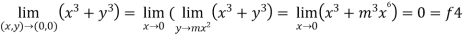
Therefore,
F1 = f2 = f3 =f4
We can say that the limit exists with 0.
Example-2: Evaluate the following-

Sol. First we will calculate f1 –
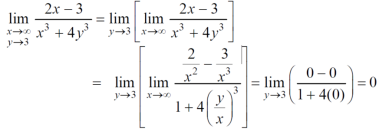
Here we see that f1 = 0
Now find f2,
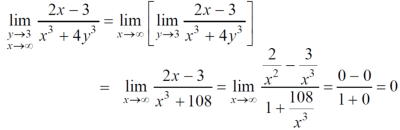
Here , f1 = f2
Therefore the limit exists with value 0.
Key takeaways:
- The function f(x,y) is said to tend to limit ‘L’ , as x →a and y→b Iff the limit is dependent on point (x,y) as x →a and y→b
- At point (a,b) , a function f(x,y) is said to be continuous if,
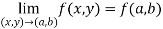
3. A function is said to be continuous in a domain if it is continuous at every point of the domain.
4. If f is not continuous at (a, b), it is said to be discontinuous at (a, b).
5. If f (x, y) and g(x, y) are continuous at (a, b) then f ± g, f · g and f /g are continuous at (a, b).
Partial differentiation is the process of finding partial derivatives. All the rules of differentiation applicable to function of a single independent variable are also applicable in partial differentiation with the only difference that while differentiating partially with respect to one variable, all the other variables are treated as constants.
First order partial differentiation-
Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as  and defined as follows:
and defined as follows:

Now the partial derivative of f with respect to f can be written as 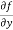 and defined as follows:
and defined as follows:
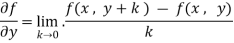
Note:
A. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
B. We apply all differentiation rules.
Higher order partial differentiation-
Let f(x, y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a) 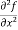 =
= 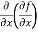
(b) 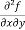 =
= 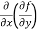
(c) 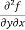 =
= 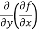
(d)  =
= 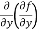
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Note-
The crossed or mixed partial derivatives 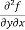 and
and  are in general, equal
are in general, equal
i.e.
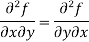
A function of 2 variables has two first order derivatives, four second order derivatives and of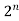 order derivatives. A function of m independent variables will have
order derivatives. A function of m independent variables will have 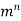 derivatives of order n.
derivatives of order n.
Example-1: Calculate 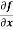 and
and 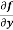 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 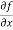 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
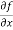 =
= 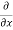 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 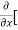 3x³] -
3x³] - 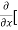 5y²] +
5y²] + 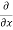 [2xy] -
[2xy] -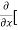 8x] +
8x] +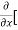 4y] -
4y] - 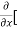 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
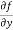 =
= 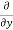 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 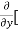 3x³] -
3x³] - 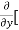 5y²] +
5y²] +  [2xy] -
[2xy] -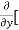 8x] +
8x] +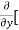 4y] -
4y] - 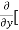 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate  and
and 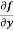 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 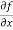 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
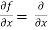 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)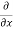 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
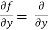 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)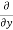 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xy cos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol.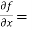 3x²y² - y⁵,
3x²y² - y⁵,  2x³y – 5xy⁴,
2x³y – 5xy⁴,
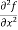 =
= 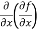 = 6xy²
= 6xy²
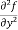 =
= 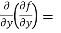 2x³ - 20xy³
2x³ - 20xy³
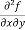 =
= 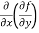 = 6x²y – 5y⁴
= 6x²y – 5y⁴
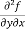 =
= 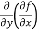 = 6x²y - 5y⁴
= 6x²y - 5y⁴
Example-4: Find
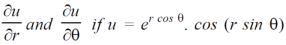
Sol. First we will differentiate partially with respect to r,
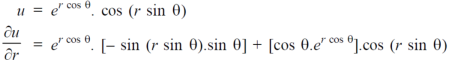
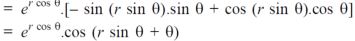
Now differentiate partially with respect to θ, we get
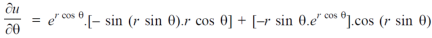
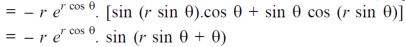
Example-5: if,
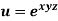
Then find.
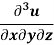
Sol-
We have
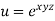
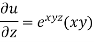
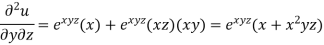

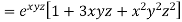
Example-6: if 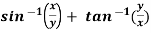 , then show that-
, then show that- 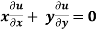
Sol. Here we have,
u = 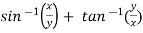 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get
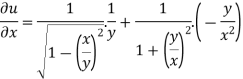
= 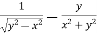
Or
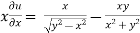 ………………..(2)
………………..(2)
And now,
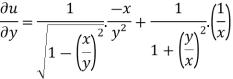
= 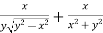
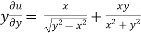 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
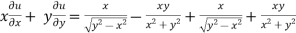 = 0
= 0
Hence proved.
Example-7: If z = 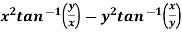
Then prove that-
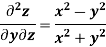
Sol.
Here we have-
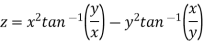
Then

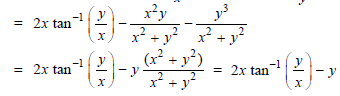
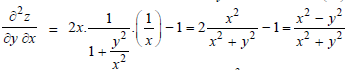
Key takeaways-
- The function f(x,y) is said to tend to limit ‘l’ , as x →a and y→b Iff the limit is dependent on point (x,y) as x →a and y→b
- Let f(x , y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as
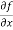 and defined as follows:
and defined as follows:
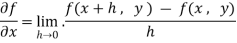
3. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating, as constant.
(a) 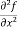 =
= 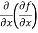
(b) 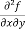 =
= 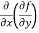
(c)  =
= 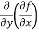
(d)  =
= 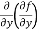
Total differential-
Total differential of a function f of three variables x, y, z is denoted by df and is defined as

Total derivative (Chain rules for partial derivatives)
Suppose u = f (x, y) and x and y are themselves functions of a single independent variable
t. Then the dependent variable f may be considered as truly a function of the one independent variable t via the intermediate variables x, y. Now the derivative of f with respect to ‘t ’ is known as the total derivative of f and is given by

Note- if u = f (x, y, z) and x = x(t ), y = y(t ), z = z(t ) then the total derivative of f is

And we can find the this result for more than three variables in same way.
Example-:1 let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t, Then find 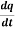 .
.
Sol:
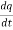 . =
. = 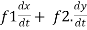
Where,
f1 = 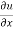 , f2 =
, f2 = 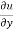
In this example f1 = 4, f2 = 3
Also,
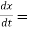 3t² + 2t,
3t² + 2t, 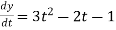
 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(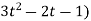
= 21t² + 2t – 3
Example-2: Find  if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Sol. As we know that by definition,  =
= 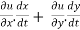
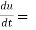 3x²y⁴3t² + 4x³y³2t = 17t¹⁶
3x²y⁴3t² + 4x³y³2t = 17t¹⁶
Example-3: if w = x² + y – z + sint and x + y = t, find
(a) 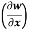 y,z
y,z
(b) 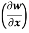 t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
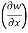 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)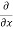 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus
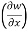 t, z = 2x - 1
t, z = 2x - 1
Example-4: If u = u( y – z , z - x , x – y) then prove that 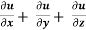 = 0
= 0
Sol. Let,
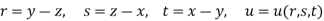
Then
By adding all these equations we get,

Hence proved.
Example-5: if φ(cx – az, cy – bz) = 0 then show that ap + bq = c
Where p =  q =
q = 
Sol. We have,
φ( cx – az , cy – bz) = 0
φ( r , s) = 0
Where,
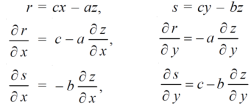
We know that,
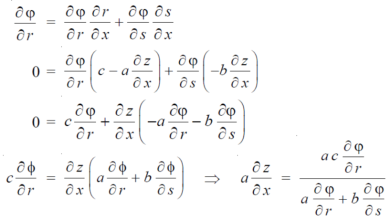
Again we do,
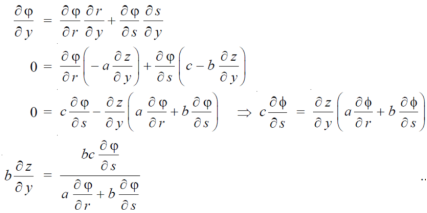
By adding the two results, we get
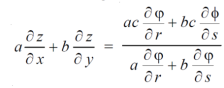

Example-6: If z is the function of x and y , and x = 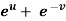 , y =
, y = 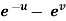 , then prove that,
, then prove that,
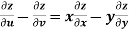
Sol.
Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
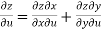 ……………….(1)
……………….(1)
And,
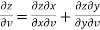 ………………..(2)
………………..(2)
Also there is,
x = 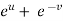 and y =
and y = 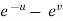 ,
,
Now,
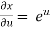 ,
, 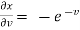 ,
,  ,
, 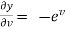
From equation(1) , we get
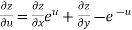 ……………….(3)
……………….(3)
And from eq. (2) , we get
 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
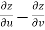 =
=  )
)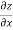 – (
– (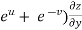
= x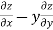
Hence proved.
Key takeaways:
- Total differential of a function f of three variables x, y, z is denoted by df and is defined as
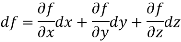
2. 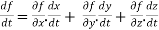
Statement- Suppose  there exists a neighborhood N(say) of (a, b) at every point of which
there exists a neighborhood N(say) of (a, b) at every point of which 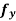 exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N.
exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N.
Proof:
Since ∂f /∂y is continuous at (a, b), there exists a neighborhood N(say) of (a, b) at every point of which 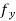 exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N
exists. We take (a + h, b + k), a point of this neighborhood so that (a + h, b),(a, b + k) also belongs to N
We write f(a + h, b + k) − f(a, b) = {f(a + h, b + k) − f(a + h, b)} + {f(a + h, b) − f(a, b)}. Consider a function of one variable φ(y) = f(a + h, y).
Since 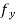 exists in N, φ(y) is differentiable with respect to y in the closed interval [b, b+k] and as such we can apply Lagrange’s Mean Value Theorem, for function of one variable y in this interval and thus obtain
exists in N, φ(y) is differentiable with respect to y in the closed interval [b, b+k] and as such we can apply Lagrange’s Mean Value Theorem, for function of one variable y in this interval and thus obtain
φ(b + k) − φ(b) = kφ’ (b + θk), 0 < θ < 1
= k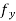 (a + h, b + θk)
(a + h, b + θk)
f(a + h, b + k) − f(a + h, b) = k (a + h, b + θk), 0 < θ < 1.
(a + h, b + θk), 0 < θ < 1.
Now, if we write 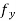 (a + h, b + θk) −
(a + h, b + θk) − 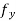 (a, b) =
(a, b) = 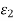 (a function of h, k)
(a function of h, k)
Then from the fact that 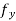 is continuous at (a,b). We may obtain
is continuous at (a,b). We may obtain
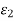 → 0 as (h, k) → (0, 0).
→ 0 as (h, k) → (0, 0).
Again because  exists at (a, b) implies
exists at (a, b) implies
f(a + h, b) − f(a, b) = h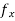 (a, b) +
(a, b) + 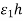 ,
,
Where 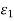 → 0 as h → 0. Combining all these we get
→ 0 as h → 0. Combining all these we get

Where 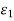 ,
, 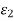 are functions of (h, k) and they tend to zero as (h, k) → (0, 0).
are functions of (h, k) and they tend to zero as (h, k) → (0, 0).
Hence, f(x, y) is differentiable at (a, b).
Example: Show that the function is differentiable at (0, 0)
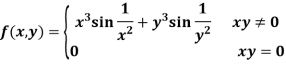
Sol:
Consider the function
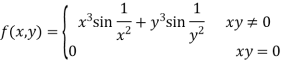
Then
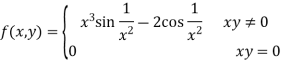
Also,
So partial derivatives are not continuous at (0, 0).

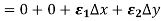
Where 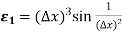 and
and 
It is easy to check that  → 0. So f is differentiable at (0, 0).
→ 0. So f is differentiable at (0, 0).
A composite function is a composition / combination of the functions. In this value of one function depends on the value of another function. A composite function is created when one function is put in another.
Let 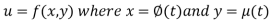
i.e 
To differentiate composite function chain rule is used:
Chain rule:
- If
 where x,y,z are all the function of t then
where x,y,z are all the function of t then

2. If 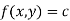 be an implicit relation between x and y.
be an implicit relation between x and y.
Differentiating with respect to x we get

We get 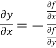
Example1: If  where
where  then find the value of
then find the value of 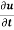 ?
?
Given 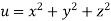
Where 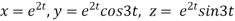
By chain rule
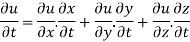
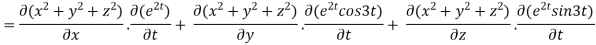
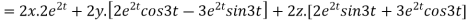
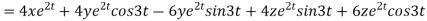
Now substituting the value of x ,y,z we get
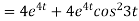 -6
-6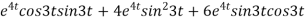
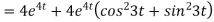
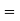 8
8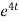
Example2: If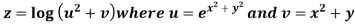 then calculate
then calculate 
Given 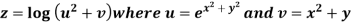
By Chain Rule
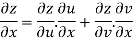
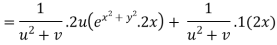
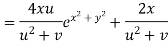
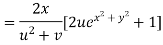
Putting the value of u = 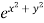
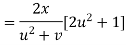
Again partially differentiating z with respect to y
By Chain Rule
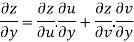
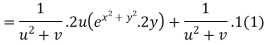
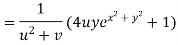
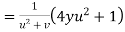 by substituting value
by substituting value 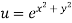
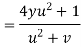
Example 3: If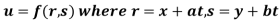 .
.
Show that 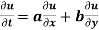
Given 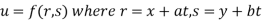
Partially differentiating u with respect to x and using chain rule
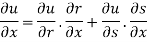
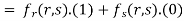
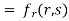 ………(i)
………(i)
Partially differentiating z with respect to y and using chain rule
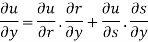
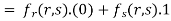
=  ………..(ii)
………..(ii)
Partially differentiating z with respect to t and using chain rule
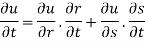
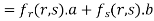
Using (i) and (ii) we get
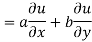
Hence 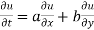
Example4: If  where the relation is
where the relation is 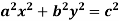 .
.
Find the value of 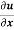
Let the given relation is denoted by 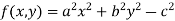
We know that 
Differentiating u with respect to x and using chain rule

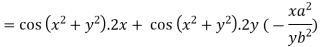
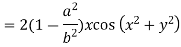
Example5: If 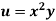 and the relation is
and the relation is 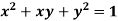 . Find
. Find 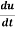
Given relation can be rewrite as
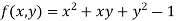 .
.
We know that
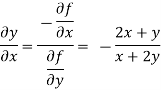
Differentiating u with respect to x and using chain rule
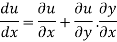
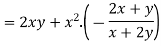
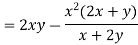
Key takeaways-
Chain rule:
- If
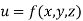 where x,y,z are all the function of t then
where x,y,z are all the function of t then
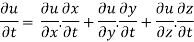
2. If 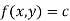 be an implicit relation between x and y.
be an implicit relation between x and y.
Differentiating with respect to x we get
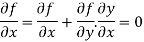
We get

Directional derivative
Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighbouring points P and Q in the field. Then,
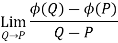
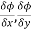 ,
,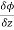 are the directional derivative of ϕ in the direction of the coordinate axes at P.
are the directional derivative of ϕ in the direction of the coordinate axes at P.
The directional derivative of ϕ in the direction l, m, n=l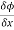 + m
+ m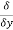 +
+ 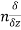
The directional derivative of ϕ in the direction of 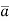 =
= 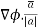
Example: Find the directional derivative of 1/r in the direction 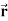 where
where 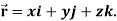
Sol. Here 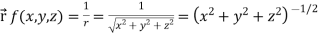
Now,
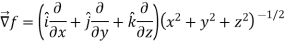
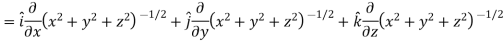
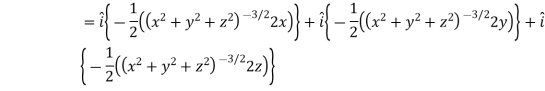
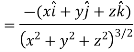
And 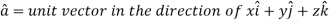
We know that-
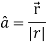
So that-
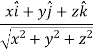
Now,
Directional derivative = 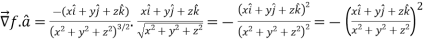
Example: Find the directional derivative of
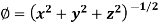
At the points (3, 1, 2) in the direction of the vector 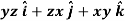 .
.
Sol. Here it is given that-
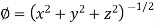
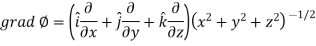
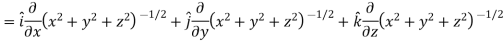
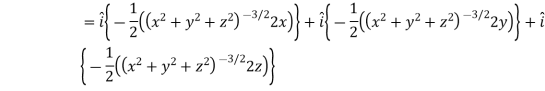
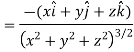
Now at the point (3, 1, 2)-
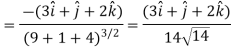
Let 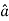 be the unit vector in the given direction, then
be the unit vector in the given direction, then
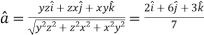 at (3, 1, 2)
at (3, 1, 2)
Now,
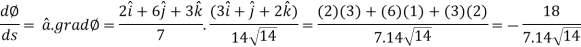
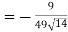
Example: Find the directional derivatives of 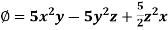 at the point P(1, 1, 1) in the direction of the line
at the point P(1, 1, 1) in the direction of the line 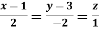
Sol. Here
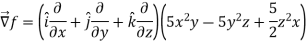
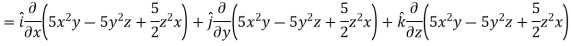
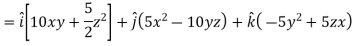
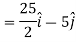
Direction ratio of the line  are 2, -2, 1
are 2, -2, 1
Now directions cosines of the line are-
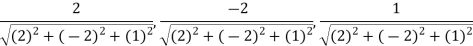
Which are 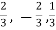
Directional derivative in the direction of the line-
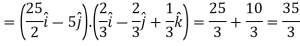
Key takeaways-
- The directional derivative of ϕ in the direction l, m, n= l
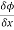 + m
+ m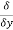 +
+ 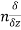
- The directional derivative of ϕ in the direction of
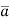 =
= 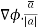
Suppose f(x, y, z) be the scalar function and it is continuously differentiable then the vector-

Is called gradient of f and we can write is as grad f.
So that-
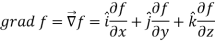
Here 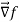 is a vector which has three components
is a vector which has three components 
Properties of gradient-
Property-1: 
Proof:
First we will take left hand side
L.H.S = 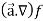
= 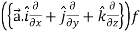
= 
= 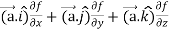
Now taking R.H.S,
R.H.S. = 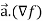
= 
= 
Here- L.H.S. = R.H.S.
Hence proved.
Property-2: Gradient of a constant (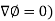
Proof:
Suppose 
Then 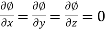
We know that the gradient-
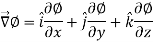
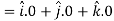
= 0
Property-3: Gradient of the sum and difference of two functions-
If f and g are two scalar point functions, then
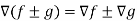
Proof:
L.H.S 

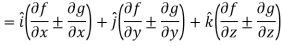
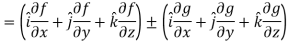
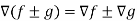
Hence proved
Property-4: Gradient of the product of two functions
If f and g are two scalar point functions, then
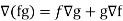
Proof:
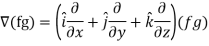
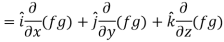
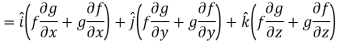
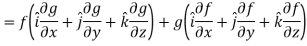
So that-
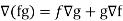
Hence proved.
Property-5: Gradient of the quotient of two functions-
If f and g are two scalar point functions, then-
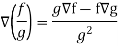
Proof:

So that-
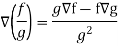
Conservative
A vector function 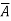 is said to be a conservative vector field if
is said to be a conservative vector field if  = ∇f i.e.,
= ∇f i.e., 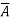 is the gradient of a scalar function f. In this case f is known as the potential function of
is the gradient of a scalar function f. In this case f is known as the potential function of 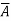 .
.
Example-1: If 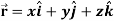 , then show that
, then show that
1. 
2. 
Sol.
Suppose 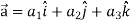 and
and 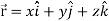
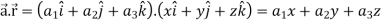
Now taking L.H.S,
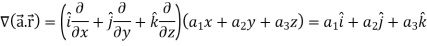
Which is 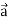
Hence proved.
2. 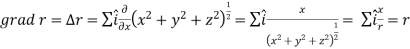
So that
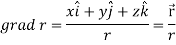
Example: If 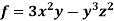 then find grad f at the point (1,-2,-1).
then find grad f at the point (1,-2,-1).
Sol.
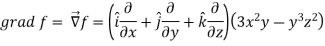
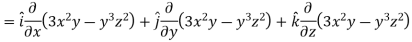
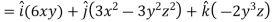
Now grad f at (1 , -2, -1) will be-
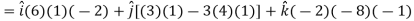
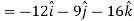
Example: If 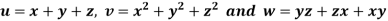 then prove that grad u, grad v and grad w are coplanar.
then prove that grad u, grad v and grad w are coplanar.
Sol.
Here- 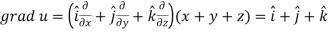

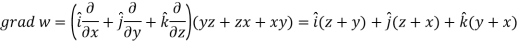
Now-
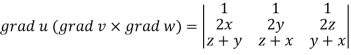
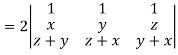
Apply 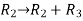

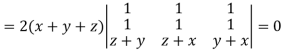
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Key takeaways:
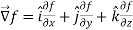
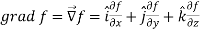
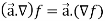
- A vector function
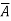 is said to be a conservative vector field if
is said to be a conservative vector field if 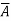 = ∇f i.e.,
= ∇f i.e., 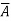 is the gradient of a scalar function f. In this case f is known as the potential function of
is the gradient of a scalar function f. In this case f is known as the potential function of 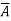 .
.
References:
1. S C Mallik and S Arora: Mathematical Analysis, New Age International.
2. Publications S Ghorpade, B V Limaye, Multivariable calculus, Springer international edition.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers.
4. Advanced engineering mathematics, by HK Dass.
5. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.