Unit - 4
Orthogonal complements
Definition:
Let V be an inner product space. A subset of V is an orthonormal basis for V if it is an ordered basis that is orthonormal.
Let S be a subset of an inner product space V. The orthogonal complement of S, denoted by 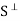 (read ‘‘S perp’’) consists of those vectors in V that are orthogonal to every vector u
(read ‘‘S perp’’) consists of those vectors in V that are orthogonal to every vector u 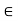 S; that is,
S; that is,

In particular, for a given vector u in V, we have

That is 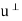 consists of all vectors in V that are orthogonal to the given vector u.
consists of all vectors in V that are orthogonal to the given vector u.
We show that 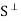 is a subspace of V. Clearly 0
is a subspace of V. Clearly 0 
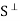 , because 0 is orthogonal to every vector in V. Now suppose v, w
, because 0 is orthogonal to every vector in V. Now suppose v, w 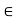
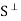 . Then, for any scalars a and b and any vector u
. Then, for any scalars a and b and any vector u 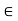 S, we have
S, we have
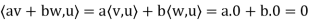
Thus, av + bw 
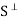 , and therefore S? is a subspace of V.
, and therefore S? is a subspace of V.
Theorem:
Le tW be a finite-dimensional subspace of an inner product space V, and let y ∈ V. Then there exist unique vectors u ∈ W and z ∈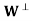 such that y = u + z. Furthermore, if {
such that y = u + z. Furthermore, if { } is an orthonormal basis for W, then
} is an orthonormal basis for W, then

Proof:
Let {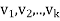 } be an orthonormal basis for W, let u be as defined in the preceding equation, and let z = y − u. Clearly u ∈ W and y = u + z.
} be an orthonormal basis for W, let u be as defined in the preceding equation, and let z = y − u. Clearly u ∈ W and y = u + z.
To show that z ∈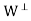 ⊥, it suffices to show, that z is orthogonal to each
⊥, it suffices to show, that z is orthogonal to each 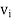 . For any j, we have
. For any j, we have
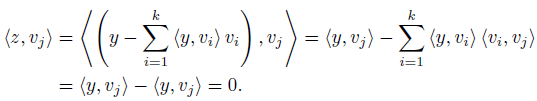
To show uniqueness of u and z, suppose that y = u + z = u’ + z’ where
U’ ∈ W and z’ ∈ W⊥. Then u – u’’ z’ − z ∈ W ∩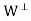 = {0 }. Therefore,
= {0 }. Therefore,
u = u’ and z = z’.
Example: Let V = 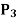 (R) with the inner product
(R) with the inner product

We compute the orthogonal projection 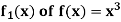 on
on 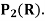
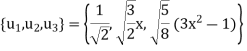
Is an orthonormal basis for 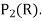 . For these vectors, we have
. For these vectors, we have
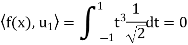
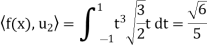
And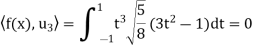
Hence
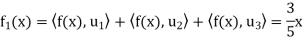
Bessel’s inequality: Let V be an inner product space, and let S = {v1, v2, . . . , vn} be an orthonormal subset of V. For any x ∈ V we have
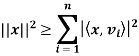
Key takeaways:
- Let V be an inner product space. A subset of V is an orthonormal basis for V if it is an ordered basis that is orthonormal.
2. For a given vector u in V, we have
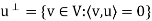
That is  consists of all vectors in V that are orthogonal to the given vector u.
consists of all vectors in V that are orthogonal to the given vector u.
We show that  is a subspace of V.
is a subspace of V.
For a linear operator T on an inner product space V, we now define a related linear operator on V called the adjoint of T, whose matrix representation with respect to any orthonormal basis  for V is
for V is  .
.
The analogy between conjugation of complex numbers and adjoints of linear operators will become apparent.
Let V be an inner product space, and let y ∈ V. The function g : V → F defined by g(x) = 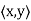 is clearly linear. More interesting is the fact that if V is finite-dimensional, every linear transformation from V into F is of this form.
is clearly linear. More interesting is the fact that if V is finite-dimensional, every linear transformation from V into F is of this form.
Theorem: Let V be a finite-dimensional inner product space over F, and let g: V → F be a linear transformation. Then there exists a unique vector y ∈ V such that g(x) = 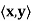 for all x ∈ V.
for all x ∈ V.
Proof:
Let  = {v1, v2, . . . , vn} be an orthonormal basis for V, and let
= {v1, v2, . . . , vn} be an orthonormal basis for V, and let
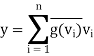
Define h: V → F by h(x) = 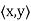 , which is clearly linear. Furthermore, for
, which is clearly linear. Furthermore, for
1 ≤ j ≤ n we have
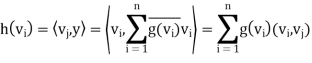
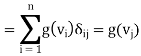
Theorem: Let V be a finite-dimensional inner product space, and let T be a linear operator on V. Then there exists a unique function T∗ : V → V such that  for all x, y ∈ V. Furthermore, T∗ is linear.
for all x, y ∈ V. Furthermore, T∗ is linear.
Proof:
Let y ∈ V. Define g: V → F by g(x) =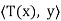 for all x ∈ V. We
for all x ∈ V. We
First show that g is linear. Let x1, x2 ∈ V and c ∈ F. Then
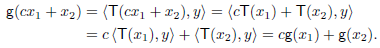
Hence g is linear.
To obtain a unique vector y’∈ V such that
g(x) = 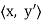 ; that is,
; that is, for all x ∈ V. Defining T∗ : V → V
for all x ∈ V. Defining T∗ : V → V
By 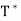 (y) = y_, we have
(y) = y_, we have 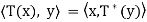 .
.
To show that 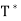 is linear, let y1, y2 ∈ V and c ∈ F. Then for any x ∈ V,
is linear, let y1, y2 ∈ V and c ∈ F. Then for any x ∈ V,
We have
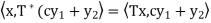
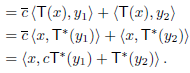
Since x is arbitrary, 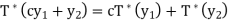
Finally, we need to show that 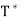 is unique. Suppose that U: V → V is linear and that it satisfies
is unique. Suppose that U: V → V is linear and that it satisfies 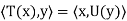 for all x, y ∈ V. Then
for all x, y ∈ V. Then 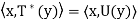 for all x, y ∈ V, So
for all x, y ∈ V, So 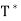 = U.
= U.
The linear operator T∗ described in this theorem is called the adjoint of the operator T. The symbol 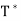 is read “T star.”
is read “T star.”
Thus T∗ is the unique operator on V satisfying 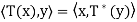 for
for
All x, y ∈ V. Note that we also have
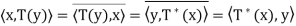
So 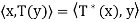 for all x, y ∈ V.
for all x, y ∈ V.
For an infinite-dimensional inner product space, the adjoint of a linear operator
T may be defined to be the function T∗ such that 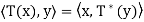 for all x, y ∈ V, provided it exists.
for all x, y ∈ V, provided it exists.
Example:
Let T be the linear operator on  defined by T(a1, a2) = (2ia1+3a2, a1−a2).
defined by T(a1, a2) = (2ia1+3a2, a1−a2).
If 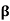 is the standard ordered basis for
is the standard ordered basis for 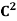 , then
, then
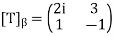
So
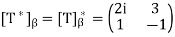
Hence

Theorem: Let V be an inner product space, and let T and U be linear operators on V. Then
(a) 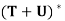 =
= 
(b) 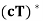 =
= 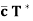 for any c ∈ F;
for any c ∈ F;
(c) 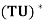 =
= 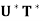
(d) 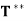 = T
= T
(e) 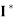 = I.
= I.
Proof:
Here we prove (a) and (d); the rest are proved similarly. Let x, y ∈ V.
(a) Because

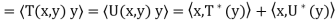
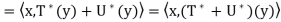
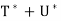 has the property unique to
has the property unique to 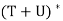 . Hence
. Hence 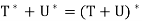
(d) Similarly, since
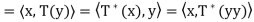
Note-
Let A and B be n × n matrices. Then
(a) 
(B) 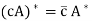 for any c ∈ F;
for any c ∈ F;
(c) 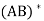 =
= 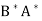
(d) 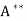 = T
= T
(e) 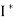 = I.
= I.
Key takeaways:
Let V be an inner product space, and let y ∈ V. The function g : V → F defined by g(x) = 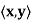 is clearly linear. More interesting is the fact that if V is finite-dimensional, every linear transformation from V into F is of this form.
is clearly linear. More interesting is the fact that if V is finite-dimensional, every linear transformation from V into F is of this form.
Suppose a survey conducted by taking two measurements such as 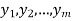 at times
at times 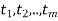 respectively.
respectively.
For example the surveyer wants to measure the birth rate at various times during a given period.
Suppose the collected data set 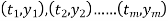 is plotted as points in the plane.
is plotted as points in the plane.
From this plot, the surveyer finds that there exists a linear relationship between the two variables, y and t, say- y = ct + d, and would like to find the constants c and d so that the line y = ct + d represents the best possible fit to the data collected. One such estimate of fit is to calculate the error E that represents the sum of the squares of the vertical distances from the points to the line; that is,
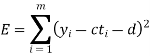

Thus we reduce this problem to finding the constants c and d that minimize
E.( the line y = ct + d is called the least squares line)
If we suppose,
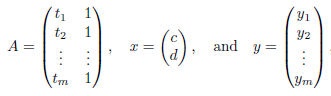
Then it follows-
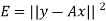
We develop a general method for finding an explicit vector 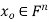 that minimizes E; that is, given an m × n matrix A, we find
that minimizes E; that is, given an m × n matrix A, we find 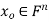 such that
such that  for all vectors
for all vectors 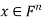 .
.
This method not only allows us to find the linear function that best fits the data, but also, for any positive integer n, the best fit using a polynomial of degree at most n.
For 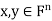 , let
, let  denote the standard inner product of x and y in
denote the standard inner product of x and y in 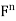 . Recall that if x and y are regarded as column vectors, then
. Recall that if x and y are regarded as column vectors, then
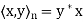
First lemma: Suppose 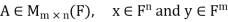 then
then
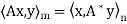
Second lemma: Suppose  , then rank(
, then rank(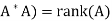
Note- If A is an m × n matrix such that rank(A) = n, then  is invertible.
is invertible.
Theorem: let 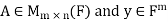 then there exists
then there exists  such that
such that 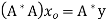 and
and 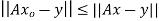 for all
for all 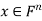 .
.
Furthermore, if rank (A) = n, then 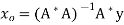
Example: Suppose the data collected by surveyor is (1, 2), (2, 3), (3, 5) and (4, 7), then
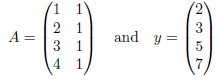
Hence
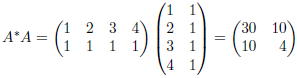
Thus
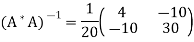
Therefore,

It follows that the line y = 1.7t is the least squares line. The error E is computed as 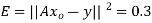
There are two types of linear equations-
1. Consistent
2. Inconsistent
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Whereas,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-




This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) Consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) Inconsistent equations-
If Rank of A ≠ Rank of C
Solution of homogeneous system of linear equations-
A system of linear equations of the form AX = O is said to be homogeneous, where A denotes the coefficients and of matrix and O denotes the null vector.
Suppose the system of homogeneous linear equations is,



It means,
AX = O
Which can be written in the form of matrix as below,
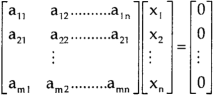
Note- A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n, then there will be an infinite number of solution.
Example: Find the solution of the following homogeneous system of linear equations,
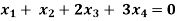

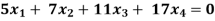
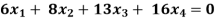
Sol. The given system of linear equations can be written in the form of matrix as follows,
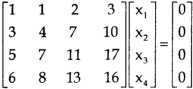
Apply the elementary row transformation,
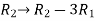

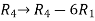 , we get,
, we get,
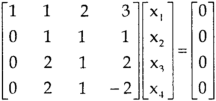
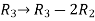
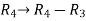 , we get
, we get
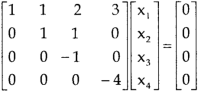
Here r(A) = 4, so that it has trivial solution,
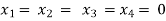
Example: Find out the value of ‘b’ in the system of homogeneous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) Trivial solution
(2) Non-trivial solution
Sol. (1)
For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
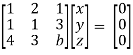
Apply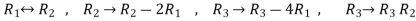
Respectively, we get the following resultant matrices
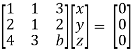
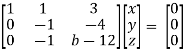
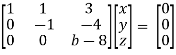
For non-trivial solutions, r(A) = 2 < n
b – 8 = 0
b = 8
Solution of non-homogeneous system of linear equations-
Example-1: check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
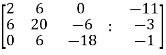
Apply  , we get
, we get
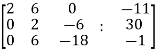
Apply 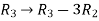

Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A, B]
That will be,
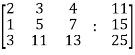
Apply 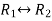
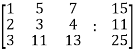
Now apply,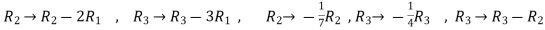
We get,
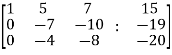 ~
~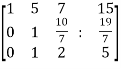 ~
~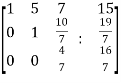
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,

That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,

From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x, y , z are 2 , -3 , 4 respectively.
Minimal Solutions to Systems of Linear Equations:
Even when a system of linear equations Ax = b is consistent, there may be no unique solution. In such cases, it may be desirable to find a solution of minimal norm. A solution s to Ax = b is called a minimal solution if ||s|| 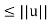 for all other solutions u. The next theorem assures that every consistent system of linear equations has a unique minimal solution and provides a method for computing it.
for all other solutions u. The next theorem assures that every consistent system of linear equations has a unique minimal solution and provides a method for computing it.
Theorem: Suppose 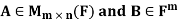 Suppose that Ax = b is consistent. Then the following statements are true.
Suppose that Ax = b is consistent. Then the following statements are true.
(a) There exists exactly one minimal solution s of Ax = b, and s ∈ R( ).
).
(b) The vector s is the only solution to Ax = b that lies in R(LA∗ ); that is,
If u satisfies (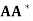 )u = b, then s =
)u = b, then s =  u.
u.
Example:
Consider the system
x + 2y + z= 4
x − y + 2z = −11
x + 5y = 19.

In order to find the minimal solution to this system, we must first find some solution u to

So we consider the system
6x + y + 11z= 4
x + 6y − 4z = −11
11x − 4y + 26z= 19
For which one solution is
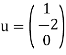
(Any solution will suffice.) Hence
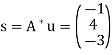
Is the minimal solution to the given system.
Key takeaways:
1. If a system of equations has no solution, then it is called inconsistent.
2. Consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
Inconsistent equations-
If Rank of A ≠ Rank of C
3. A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n, then there will be an infinite number of solution.
Here we will start the concept with a lemma.
Lemma: Let T be a linear operator on a finite-dimensional inner product space V. If T has an eigenvector, then so does 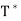
Proof:
Suppose that v is an eigenvector of T with corresponding eigenvalue 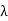 . Then for any x ∈ V,
. Then for any x ∈ V,
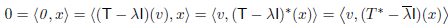
And hence v is orthogonal to the range of  . So
. So  is not onto
is not onto
And hence is not one-to-one.
Thus 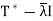 has a nonzero null space, and any nonzero vector in this null space is an eigenvector of
has a nonzero null space, and any nonzero vector in this null space is an eigenvector of 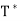 with corresponding eigenvalue
with corresponding eigenvalue 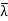 .
.
Note-
- A subspace W of V is said to be T-invariant if T(W) is contained in W. If W is Tinvariant, we may define the restriction TW: W → W by TW(x) = T(x) for all x ∈ W. It is clear that TW is a linear operator on W. Recall
- A polynomial is said to split if it factors into linear polynomials.
Theorem: Let T be a linear operator on a finite dimensional inner product space V. Suppose that the characteristic polynomial of T splits. Then there exists an orthonormal basis 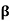 for V such that the matrix
for V such that the matrix  is upper triangular.
is upper triangular.
Definition:
Let V be an inner product space, and let T be a linear operator on V. We say that T is normal if T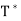 =
= 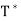 T. An n × n real or complex matrix A is normal if A
T. An n × n real or complex matrix A is normal if A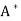 =
= 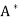 A.
A.
Note- T is normal if and only if 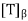 is normal, where
is normal, where is an orthonormal basis.
is an orthonormal basis.
For example: Suppose that A is a real skew-symmetric matrix; that is, 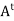 = −A. Then A is normal because both A
= −A. Then A is normal because both A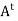 and
and 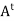 A are equal to −
A are equal to −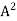 .
.
General properties of normal operators:
Let V be an inner product space, and let T be a normal operator on V. Then the following statements are true.
(a) ||T(x)|| = ||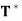 (x)|| for all x ∈ V.
(x)|| for all x ∈ V.
(b) (b) T − cI is normal for every c ∈ F.
(c) If x is an eigenvector of T, then x is also an eigenvector of T∗. In fact, if T(x) = λx, then 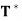 (x) =
(x) = 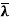 x.
x.
(d) If 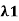 and
and 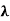 2 are distinct eigenvalues of T with corresponding eigenvectors x1 and x2, then x1 and x2 are orthogonal.
2 are distinct eigenvalues of T with corresponding eigenvectors x1 and x2, then x1 and x2 are orthogonal.
Proof:
(a) For any x ∈ V, we have

(b) Do yourself
(c) Suppose that T(x) =  x for some x ∈ V. Let U = T −
x for some x ∈ V. Let U = T −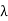 I. Then U(x) = 0, and U is normal by (b). Thus (a) implies that
I. Then U(x) = 0, and U is normal by (b). Thus (a) implies that

(d) Let 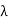 1 and
1 and 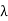 2 be distinct eigenvalues of T with corresponding eigenvectors x1 and x2. Then, using (c), we have
2 be distinct eigenvalues of T with corresponding eigenvectors x1 and x2. Then, using (c), we have
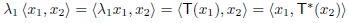
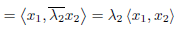
Since 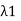 =
= 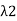 we conclude that
we conclude that 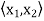 = 0.
= 0.
Definition:
Let T be a linear operator on an inner product space V. We say that T is self-adjoint (Hermitian) if T = 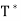 . An n × n real or complex matrix A is self-adjoint (Hermitian) if A =
. An n × n real or complex matrix A is self-adjoint (Hermitian) if A = 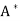 .
.
Note-
- A linear operator on a real inner product space has only real eigenvalues. The lemma that follows shows that the same can be said for self-adjoint operators on a complex inner product space.
- The characteristic polynomial of every linear operator on a complex inner product space splits, and the same is true for self-adjoint operators on a real inner product space.
Lemma: Let T be a self-adjoint operator on a finite-dimensional inner product space V. Then
(a) Every eigenvalue of T is real.
(b) Suppose that V is a real inner product space. Then the characteristic polynomial of T splits.
Proof:
(a) Suppose that T(x) = 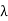 x for x _= 0. Because a self-adjoint operator is also normal
x for x _= 0. Because a self-adjoint operator is also normal
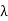 x = T(x) =
x = T(x) =  x) =
x) = 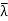 x.
x.
So λ =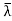 ; that is,
; that is,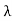 is real.
is real.
(b) Let n = dim(V),  be an orthonormal basis for V, and A =
be an orthonormal basis for V, and A = 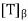 . Then A is self-adjoint. Let
. Then A is self-adjoint. Let 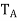 be the linear operator on
be the linear operator on 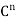 defined by
defined by 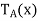 = Ax for all x ∈
= Ax for all x ∈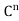 . Note that
. Note that 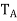 is self-adjoint because
is self-adjoint because 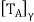 = A, where γ is the standard ordered (orthonormal) basis for
= A, where γ is the standard ordered (orthonormal) basis for 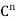 , So, by (a), the eigenvalues of
, So, by (a), the eigenvalues of 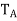 are real. By the fundamental theorem of algebra,
are real. By the fundamental theorem of algebra,
The characteristic polynomial of 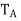 splits into factors of the form t −
splits into factors of the form t − 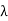 . Since each
. Since each 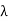 is real, the characteristic polynomial splits over R. But
is real, the characteristic polynomial splits over R. But 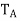 has the same characteristic polynomial as A, which has the same characteristic polynomial as T. Therefore the characteristic polynomial of T splits.
has the same characteristic polynomial as A, which has the same characteristic polynomial as T. Therefore the characteristic polynomial of T splits.
Theorem: Let T be a linear operator on a finite-dimensional real inner product space V. Then T is self-adjoint if and only if there exists an orthonormal basis β for V consisting of eigenvectors of T.
Proof:
Suppose that T is self-adjoint. By the lemma, we may apply Schur’s theorem to obtain an orthonormal basis β for V such that the matrix A = 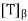 is upper triangular. But
is upper triangular. But
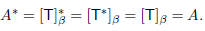
So A and 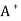 are both upper triangular, and therefore A is a diagonal matrix.
are both upper triangular, and therefore A is a diagonal matrix.
Thus β must consist of eigenvectors of T.
Key takeaways:
- Let T be a linear operator on a finite-dimensional inner product space V. If T has an eigenvector, then so does
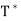
- A polynomial is said to split if it factors into linear polynomials.
- Let T be a linear operator on an inner product space V. We say that T is self-adjoint (Hermitian) if T =
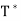 . An n × n real or complex matrix A is self-adjoint (Hermitian) if A =
. An n × n real or complex matrix A is self-adjoint (Hermitian) if A = 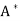 .
.
Let V be an inner product space, and let T: V → V be a projection. We say that T is an orthogonal projection if R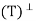 = N(T) and N
= N(T) and N = R(T).
= R(T).
Theorem: Let V be an inner product space, and let T be a linear operator on V. Then T is an orthogonal projection if and only if T has an adjoint 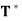 and
and 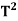 = T =
= T = 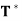 .
.
Proof:
Suppose that T is an orthogonal projection. Since  = T because T is a projection, we need to show that T∗ exists and T =
= T because T is a projection, we need to show that T∗ exists and T =  . Now V = R(T) ⊕ N(T) and R
. Now V = R(T) ⊕ N(T) and R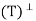 = N(T). Let x, y ∈ V. Then we can write x = x1 + x2 and y = y1 + y2, where x1, y1 ∈ R(T) and x2, y2 ∈ N(T). Hence
= N(T). Let x, y ∈ V. Then we can write x = x1 + x2 and y = y1 + y2, where x1, y1 ∈ R(T) and x2, y2 ∈ N(T). Hence

And
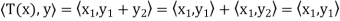
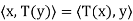 for all x, y ∈ V; thus
for all x, y ∈ V; thus 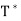 exists and T =
exists and T =  .
.
Now suppose 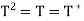 then T is a projection, hence we must show that R(T) = N
then T is a projection, hence we must show that R(T) = N and R
and R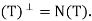
Let x ∈ R(T) and y ∈ N(T). Then x = T(x) = , and so
, and so

Therefore x ∈ N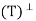 , from which it follows that R(T) ⊆ N
, from which it follows that R(T) ⊆ N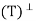 .
.
Let y ∈ N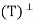 . We must show that y ∈ R(T), that is, T(y) = y. Now
. We must show that y ∈ R(T), that is, T(y) = y. Now
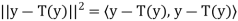

Since y − T(y) ∈ N(T), the first term must equal zero. But also
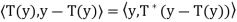
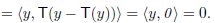
Thus y − T(y) = 0; that is, y = T(y) ∈ R(T). Hence R(T) = N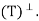
The spectral theorem
Let that T is a linear operator on a finite-dimensional inner product space V over F with the distinct eigenvalues 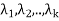 . Assume that T is normal if F = C and that T is self-adjoint if F = R. For each i (1 ≤ i ≤ k), let Wi be the eigenspace of T corresponding to the eigenvalue
. Assume that T is normal if F = C and that T is self-adjoint if F = R. For each i (1 ≤ i ≤ k), let Wi be the eigenspace of T corresponding to the eigenvalue 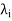 , and let
, and let 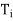 be the orthogonal projection of V on
be the orthogonal projection of V on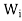 . Then the following statements are true.
. Then the following statements are true.
(a) V = W1 ⊕ W2 ⊕ ·· · ⊕ Wk.
(b) If 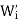 denotes the direct sum of the subspaces
denotes the direct sum of the subspaces  for j
for j 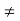 i, then
i, then 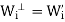
(c) 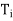
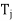 =
= 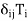 for 1 ≤ i, j ≤ k.
for 1 ≤ i, j ≤ k.
(d) I = 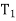 +
+ 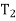 + · · · +
+ · · · + 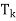 .
.
(e) T = 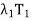 +
+ 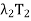 + · · · +
+ · · · + 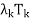
Proof:
(a) As we know that T is diagonalizable,
So that,
V = W1 ⊕ W2 ⊕ ·· · ⊕ Wk
(b)
If x ∈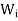 and y ∈
and y ∈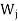 for some I is not equals to j, then
for some I is not equals to j, then 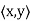 = 0.
= 0.
It follows easily from this result that 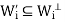
From first result, we have
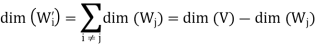
On the other hand, we have
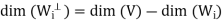
Hence
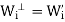
Proof of (d)-
Since Ti is the orthogonal projection of V on 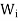 , it follows from
, it follows from
(b) that N(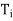 ) = R(
) = R(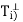 =
= 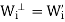
Hence, for x ∈ V, we have x = x1 + x2 + · · · + xk, where 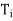 (x) =
(x) =  ∈
∈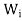 .
.
Now we will prove the last result,
For x ∈ V, write x = x1 + x2 + · · · + xk, where xi ∈ . Then
. Then
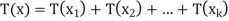
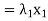 +
+ 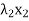 + · · · +
+ · · · + 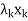
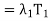 (x) +
(x) + 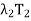 (x) + · · · +
(x) + · · · + 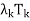 (x)
(x)
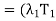 +
+ 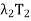 + · · · +
+ · · · +  )x
)x
The set {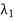 ,
, 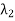 , . . . ,
, . . . ,  } of eigenvalues of T is called the spectrum of T, the sum I =
} of eigenvalues of T is called the spectrum of T, the sum I = 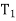 +
+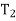 +· · ·+
+· · ·+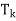 in (d) is known as resolution of the identity operator induced by T, and the sum T =
in (d) is known as resolution of the identity operator induced by T, and the sum T = 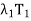 +
+ 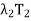 + · · · +
+ · · · + 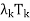 in (e) is called the spectral decomposition of T. The spectral decomposition of T is unique up to the order of its eigenvalues.
in (e) is called the spectral decomposition of T. The spectral decomposition of T is unique up to the order of its eigenvalues.
Note-
The spectral theorem can also be stated as below-
Let T be a normal (symmetric) operator on a complex (real) finite-dimensional inner product space V. Then there exists linear operators 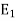 ; . . . ;
; . . . ;  on V and scalars
on V and scalars 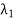 . . .
. . . 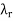 such that
such that
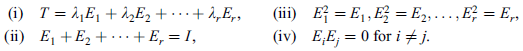
The above linear operators 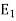 ; . . . ;
; . . . ;  are projections in the sense that
are projections in the sense that 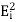 =
= 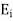 . Moreover, they are said to be orthogonal projections because they have the additional property that
. Moreover, they are said to be orthogonal projections because they have the additional property that 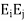 0 for
0 for 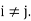
Key takeaways:
- Let V be an inner product space, and let T: V → V be a projection. We say that T is an orthogonal projection if R
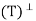 = N(T) and N
= N(T) and N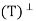 = R(T).
= R(T). - Let T be a normal (symmetric) operator on a complex (real) finite-dimensional inner product space V. Then there exists linear operators
 ; . . . ;
; . . . ; 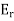 on V and scalars
on V and scalars 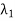 . . .
. . . 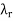 such that
such that
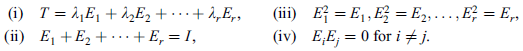
References:
1. Rao A R and Bhim Sankaram Linear Algebra Hindustan Publishing house.
2.Gilbert Strang, Linear Algebra and its Applications, Thomson, 2007.
3. Stephen H. Friedberg, Arnold J. Insel, Lawrence E. Spence, Linear Algebra (4th Edition), Pearson, 2018.
4. Linear Algebra, Seymour Lipschutz, Marc Lars Lipson, Schaum’s Outline Series