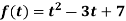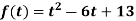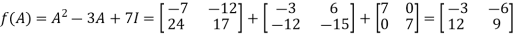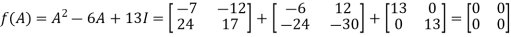Unit – 3
Eigenspaces of a linear operator
The diagonalizability can be defined in two ways:
Matrix concept:
Suppose an n-square matrix A is given. The matrix A is said to be diagonalizable if there exists a nonsingular matrix P such that
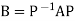
Is diagonal. This chapter discusses the diagonalization of a matrix A. In particular, an algorithm is given to find the matrix P when it exists.
Linear operator concept:
Suppose a linear operator T: V 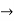 V is given. The linear operator T is said to be diagonalizable if there exists a basis S of V such that the matrix representation of T relative to the basis S is a diagonal matrix D.
V is given. The linear operator T is said to be diagonalizable if there exists a basis S of V such that the matrix representation of T relative to the basis S is a diagonal matrix D.
This chapter discusses conditions under which the linear operator T is diagonalizable.
Equivalence of the matrix and linear operator concept:
A square matrix A may be viewed as a linear operator F defined by
F(X) = AX
Where X is a column vector, and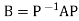 represents F relative to a new coordinate system (basis) S whose elements are the columns of P. On the other hand, any linear operator T can be represented by a matrix A relative to one basis and, when a second basis is chosen, T is represented by the matrix
represents F relative to a new coordinate system (basis) S whose elements are the columns of P. On the other hand, any linear operator T can be represented by a matrix A relative to one basis and, when a second basis is chosen, T is represented by the matrix
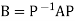
Where P is the change-of-basis matrix.
Many theorems will be stated in two ways: one in terms of matrices A and again in terms of linear mappings T.
Polynomials of Matrices:
Consider a polynomial 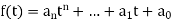 over a field K. That if A is any square matrix, then we define
over a field K. That if A is any square matrix, then we define
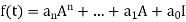
Where I is the identity matrix. In particular, we say that A is a root of f(t) if f(A) = 0, the zero matrix.
THEOREM:
Let f and g be polynomials. For any square matrix A and scalar k,
- (f + g) = f(A) + g(A)
- (fg)(A) = f(A) g(A)
- (kf)(A) = kf(A)
- f(A) g(A) = g(A)f(A)
Matrices and Linear Operators:
Now suppose that T: V  V is a linear operator on a vector space V. Powers of T are defined by the composition operation:
V is a linear operator on a vector space V. Powers of T are defined by the composition operation:
Also, for any polynomial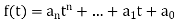 , we define f ðTÞ in the same way as we did for matrices:
, we define f ðTÞ in the same way as we did for matrices:
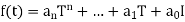
Where I is now the identity mapping. We also say that T is a zero or root of f ðtÞ if f(T) = 0; the zero mapping. We note that the relations in Theorem(above) hold for linear operators as they do for matrices.
Note- Suppose A is a matrix representation of a linear operator T. Then f (A) is the matrix representation of f(T), and, in particular, f (T) = 0 if and only if f(A) = 0.
Eigenvalues and Eigenvectors:
Let A be any n-square matrix. Then A can be represented by (or is similar to) a diagonal matrix
D = diag(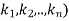 if and only if there exists a basis S consisting of (column) vectors
if and only if there exists a basis S consisting of (column) vectors 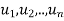
Such that
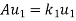
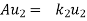
………………
……………….
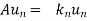
In such a case, A is said to be diagonizable. Furthermore, 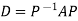
, where P is the nonsingular matrix whose columns are, respectively, the basis vectors 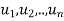
Def: Let A be any square matrix. A scalar 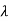 is called an eigenvalue of A if there exists a nonzero (column) vector v such that
is called an eigenvalue of A if there exists a nonzero (column) vector v such that
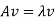
Any vector satisfying this relation is called an eigenvector of A belonging to the
Eigenvalue 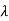 .
.
Here note that each scalar multiple kv of an eigenvector v belonging to 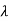 is also such an eigenvector, because
is also such an eigenvector, because
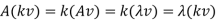
The set 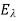 of all such eigenvectors is a subspace of V, called the eigenspace of
of all such eigenvectors is a subspace of V, called the eigenspace of 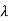 . (If dim
. (If dim 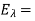 1, then
1, then 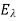 is called an eigenline and
is called an eigenline and 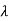 is called a scaling factor.)
is called a scaling factor.)
The terms characteristic value and characteristic vector are sometimes used instead of eigenvalue and eigenvector.
Theorem: An n-square matrix A is similar to a diagonal matrix D if and only if A has n linearly independent eigenvectors. In this case, the diagonal elements of D are the corresponding eigenvalues and 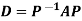 , where P is the matrix whose columns are the eigenvectors.
, where P is the matrix whose columns are the eigenvectors.
Suppose a matrix A can be diagonalized as above, say 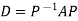 , where D is diagonal. Then A has the extremely useful diagonal factorization:
, where D is diagonal. Then A has the extremely useful diagonal factorization:
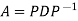
Using this factorization, the algebra of A reduces to the algebra of the diagonal matrix D, which can be
Easily calculated. Specifically, suppose D = diag(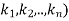 Then
Then
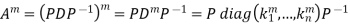
More generally, for any polynomial f(t),
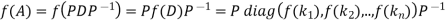
Furthermore, if the diagonal entries of D are nonnegative, let
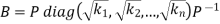
Then B is a nonnegative square root of A; that is, 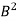 = A and the eigenvalues of B are nonnegative.
= A and the eigenvalues of B are nonnegative.
Properties of Eigenvalues and Eigenvectors:
Let A be a square matrix. Then the following are equivalent.
(i) A scalar 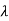 is an eigenvalue of A.
is an eigenvalue of A.
(ii) The matrix M = A - 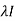 is singular.
is singular.
(iii) The scalar 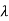 is a root of the characteristic polynomial
is a root of the characteristic polynomial 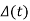 of A.
of A.
The eigenspace 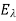 of an eigenvalue
of an eigenvalue 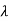 is the solution space of the homogeneous system MX = 0,
is the solution space of the homogeneous system MX = 0,
Where M = A - 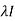 ; that is, M is obtained by subtracting
; that is, M is obtained by subtracting 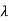 down the diagonal of A.
down the diagonal of A.
Note-
- Some matrices have no eigenvalues and hence no eigenvectors.
- Let A be a square matrix over the complex field C. Then A has at least one eigenvalue.
The geometric multiplicity of an eigenvalue 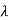 of a matrix A does not exceed its algebraic multiplicity.
of a matrix A does not exceed its algebraic multiplicity.
Suppose 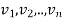 are nonzero eigenvectors of a matrix A belonging to distinct eigenvalues
are nonzero eigenvectors of a matrix A belonging to distinct eigenvalues 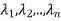 . Then
. Then 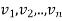 are linearly independent.
are linearly independent.
Diagonalization of matrices
Two square matrix 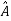 and A of same order n are s aid to be similar if and only if
and A of same order n are s aid to be similar if and only if
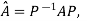 for some non singular matrix P.
for some non singular matrix P.
Such transformation of the matrix A into 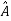 with the help of non singular matrix P is known as similarity transformation.
with the help of non singular matrix P is known as similarity transformation.
Similar matrices have the same Eigen values.
If X is an Eigen vector of matrix A then 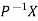 is Eigen vector of the matrix
is Eigen vector of the matrix 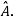
Reduction to Diagonal Form:
Let A be a square matrix of order n has n linearly independent Eigen vectors Which form the matrix P such that
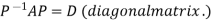
Where P is called the modal matrix and D is known as spectral matrix.
Procedure: let A be a square matrix of order 3.
Let three Eigen vectors of A are 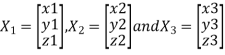 Corresponding to Eigen values
Corresponding to Eigen values 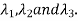
Let 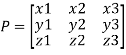
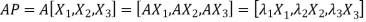 {by characteristics equation of A}
{by characteristics equation of A}
Or 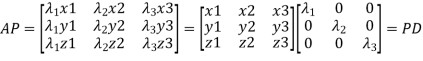
Or 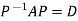
Note: The method of diagonalization is helpful in calculating power of a matrix.
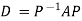 .Then for an integer n we have
.Then for an integer n we have 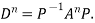
Example: Diagonalise the matrix 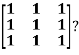
Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 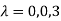 .
.
Then 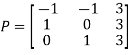 and
and 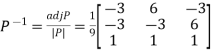
Also we know that 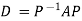
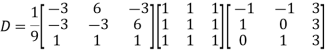
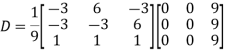
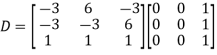
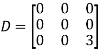
Example: Diagonalise the matrix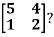
Let A =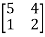
The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values 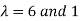 .
.
Then 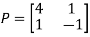 and also
and also 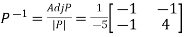
Also we know that 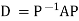
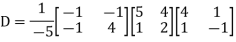
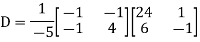

Diagonalization of Linear Operators:
Consider a linear operator T: V  V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = {
V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = {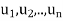 } of V for which
} of V for which
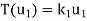
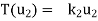
………………
……………….
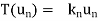
In such a case, T is represented by the diagonal matrix
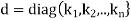
Relative to the basis S.
DEFINITION: Let T be a linear operator. A scalar 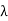 is called an eigenvalue of T if there exists a nonzero vector v such that T(v) =
is called an eigenvalue of T if there exists a nonzero vector v such that T(v) =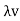 .
.
Every vector satisfying this relation is called an eigenvector of T belonging to the eigenvalue 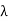 .
.
The algebraic and geometric multiplicities of an eigenvalue 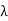 of a linear operator T are defined in the same way as those of an eigenvalue of a matrix A.
of a linear operator T are defined in the same way as those of an eigenvalue of a matrix A.
Note-
- T can be represented by a diagonal matrix D if and only if there exists a basis S of V consisting of eigenvectors of T. In this case, the diagonal elements of D are the corresponding eigenvalues.
- Let T be a linear operator. Then the following are equivalent:
(i) A scalar 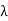 is an eigenvalue of T.
is an eigenvalue of T.
(ii) The linear operator 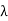 I - T is singular.
I - T is singular.
(iii) The scalar 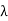 is a root of the characteristic polynomial
is a root of the characteristic polynomial 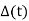 of T.
of T.
3. Suppose V is a complex vector space. Then T has at least one eigenvalue.
4. Suppose 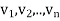 are nonzero eigenvectors of a linear operator T belonging to distinct eigenvalues
are nonzero eigenvectors of a linear operator T belonging to distinct eigenvalues 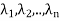 . Then
. Then 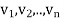 are linearly independent.
are linearly independent.
5. The geometric multiplicity of an eigenvalue l of T does not exceed its algebraic multiplicity.
6. Suppose A is a matrix representation of T. Then T is diagonalizable if and only if A is diagonalizable.
Characteristic equation:
Let A he a square matrix, 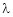 be any scalar then
be any scalar then 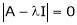 is called characteristic equation of a matrix A.
is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘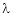 ’ be any scalar then,
’ be any scalar then,
1) 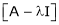 is called characteristic matrix
is called characteristic matrix
2) 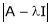 is called characteristic polynomial.
is called characteristic polynomial.
The roots of a characteristic equation are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Eigen vector:
Suppose 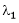 be an Eigen value of a matrix A. Then
be an Eigen value of a matrix A. Then 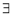 a non – zero vector x1 such that.
a non – zero vector x1 such that.
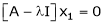 … (1)
… (1)
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value 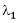 .
.
Properties of Eigen values:
- Then sum of the Eigen values of a matrix A is equal to sum of the diagonal elements of a matrix A.
- The product of all Eigen values of a matrix A is equal to the value of the determinant.
- If
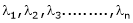 are n Eigen values of square matrix A then
are n Eigen values of square matrix A then  are m Eigen values of a matrix A-1.
are m Eigen values of a matrix A-1. - The Eigen values of a symmetric matrix are all real.
- If all Eigen values are non –zero then A-1 exist and conversely.
- The Eigen values of A and A’ are same.
Properties of Eigen vector:
- Eigen vector corresponding to distinct Eigen values are linearly independent.
- If two are more Eigen values are identical then the corresponding Eigen vectors may or may not be linearly independent.
- The Eigen vectors corresponding to distinct Eigen values of a real symmetric matrix are orthogonal.
Example1: Find the sum and the product of the Eigen values of 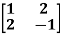 ?
?
Sol. The sum of Eigen values = the sum of the diagonal elements
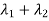 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
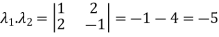
On solving above equations we get 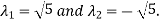
Example2: Find out the Eigen values and Eigen vectors of 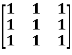
Sol. The Characteristics equation is given by 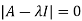
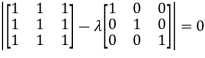
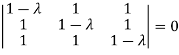
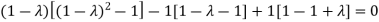
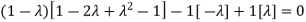
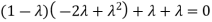
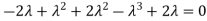
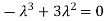
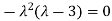
Or 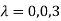
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 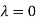 is
is
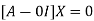
Where X is the column matrix of order 3 i.e.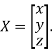
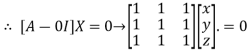
This implies that 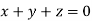
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 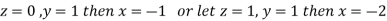
Thus the Eigen vectors corresponding to the Eigen value 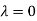 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 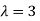 is
is
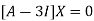
Where X is the column matrix of order 3 i.e.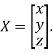
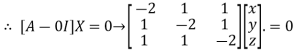
This implies that 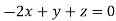
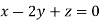
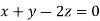
Taking last two equations we get
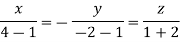
Or 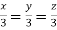
Thus the Eigen vectors corresponding to the Eigen value 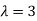 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Example3: Find out the Eigen values and Eigen vectors of 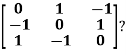
Sol. Let A =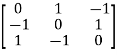
The characteristics equation of A is 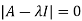 .
.
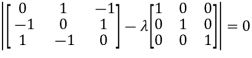
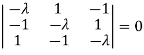
Or 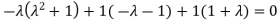
Or 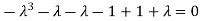
Or 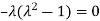
Or 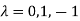
The Eigen vector corresponding to Eigen value 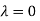 is
is
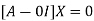
Where X is the column matrix of order 3 i.e.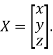
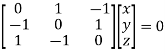
Or 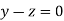
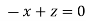
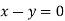
On solving we get 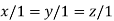
Thus the Eigen vectors corresponding to the Eigen value 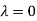 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 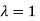 is
is
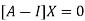
Where X is the column matrix of order 3 i.e.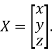
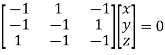
Or 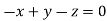
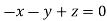
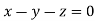
On solving 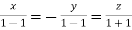 or
or 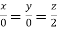 .
.
Thus the Eigen vectors corresponding to the Eigen value 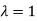 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 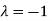 is
is
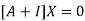
Where X is the column matrix of order 3 i.e.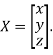
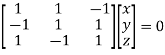
Or 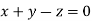
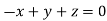
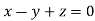
On solving we get 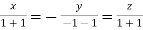 or
or 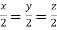 .
.
Thus the Eigen vectors corresponding to the Eigen value 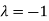 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Example-1: Determine the Eigen values of Eigen vector of the matrix.
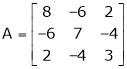
Solution:
Consider the characteristic equation as, 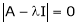
i.e. 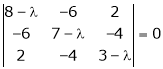
i.e. 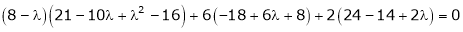
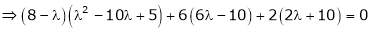
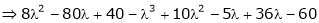
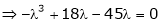
i.e. 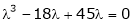
Which is the required characteristic equation.
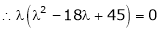
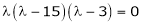
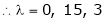 are the required Eigen values.
are the required Eigen values.
Now consider the equation
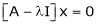 … (1)
… (1)
Case I:
If 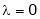 Equation (1) becomes
Equation (1) becomes
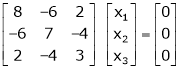
R1 + R2
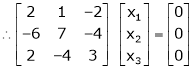
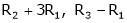
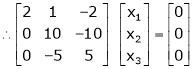
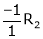
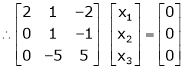
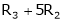
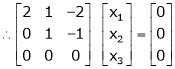
Thus 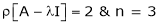
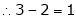 independent variable.
independent variable.
Now rewrite equation as,
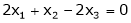
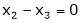
Put x3 = t
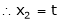 &
&
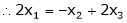
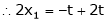
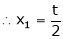
Thus 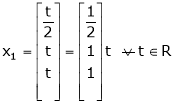 .
.
Is the eigen vector corresponding to 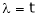 .
.
Case II:
If 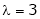 equation (1) becomes,
equation (1) becomes,
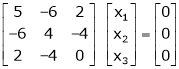
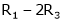
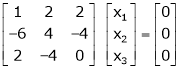
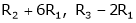
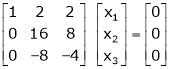
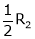
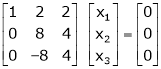
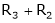
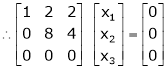
Here 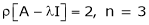
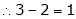 Independent variables
Independent variables
Now rewrite the equations as,
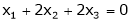
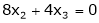
Put 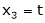
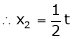 &
&
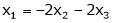
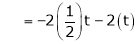
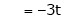
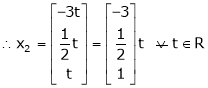 .
.
Is the eigen vector corresponding to 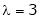 .
.
Case III:
If 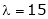 equation (1) becomes,
equation (1) becomes,
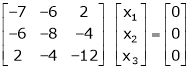
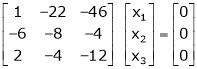
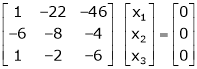
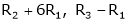
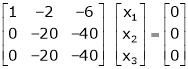
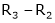
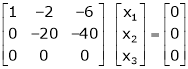
Here rank of 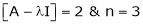
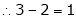 independent variable.
independent variable.
Now rewrite the equations as,
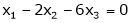
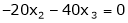
Put 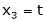
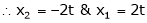
Thus 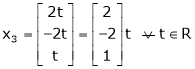 .
.
Is the eigen vector for 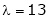 .
.
Example 2
Find the Eigen values of Eigen vector for the matrix.
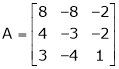
Solution:
Consider the characteristic equation as 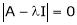
i.e. 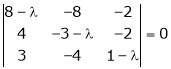
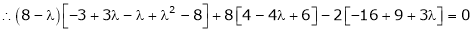
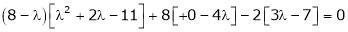
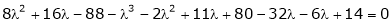
i.e. 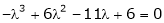
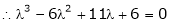
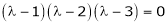
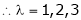 are the required eigen values.
are the required eigen values.
Now consider the equation
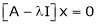 … (1)
… (1)
Case I:
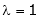 Equation (1) becomes,
Equation (1) becomes,
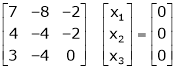
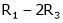
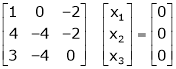
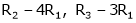
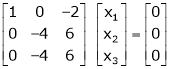
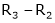
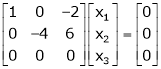
Thus 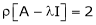 and n = 3
and n = 3
 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,
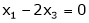
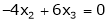
Put 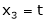
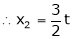 ,
, 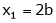
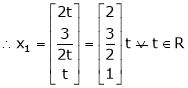
I.e.
The Eigen vector for 
Case II:
If  equation (1) becomes,
equation (1) becomes,
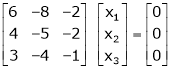
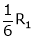
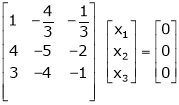
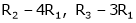
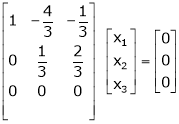
Thus 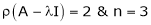
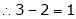
Independent variables.
Now rewrite the equations as,
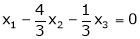
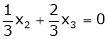
Put 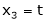
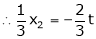
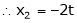
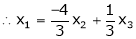
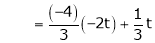
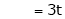
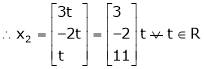
Is the Eigen vector for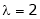
Now
Case III:-
If 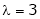 equation (1) gives,
equation (1) gives,
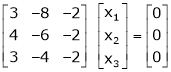
R1 – R2
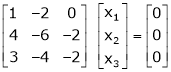
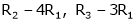
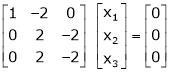
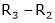
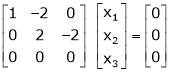
Thus 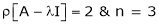
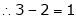
Independent variables
Now 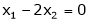
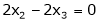
Put 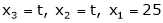
Thus
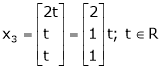
Is the Eigen vector for
Key takeaways:
- Suppose an n-square matrix A is given. The matrix A is said to be diagonalizable if there exists a nonsingular matrix P such that
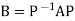
Is diagonal.
2. A square matrix A may be viewed as a linear operator F defined by
F(X) = AX
Where X is a column vector, and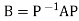 represents F relative to a new coordinate system (basis) S whose elements are the columns of P.
represents F relative to a new coordinate system (basis) S whose elements are the columns of P.
3. Let A be any square matrix. A scalar 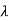 is called an eigenvalue of A if there exists a nonzero (column) vector v such that
is called an eigenvalue of A if there exists a nonzero (column) vector v such that
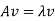
4. Let A be a square matrix of order n has n linearly independent Eigen vectors Which form the matrix P such that
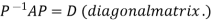
Invariant subspaces:
Let T:V 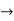 V be linear. A subspace W of V is said to be invariant under T or T-invariant if T maps W into itself—that is, if v
V be linear. A subspace W of V is said to be invariant under T or T-invariant if T maps W into itself—that is, if v 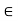 W implies T(v)
W implies T(v) 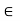 W. In this case, T restricted to W defines a linear operator on
W. In this case, T restricted to W defines a linear operator on
W; that is, T induces a linear operator T: W 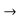 W defined by
W defined by 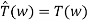 for every w
for every w 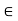 W.
W.
Example:
Let T: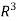
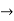
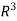 be the following linear operator, which rotates each vector v about the z-axis by an angle
be the following linear operator, which rotates each vector v about the z-axis by an angle 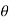
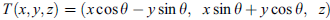
Observe that each vector w = (a, b, 0) in the xy-plane W remains in W under the mapping T; hence, W is T-invariant. Observe also that the z-axis U is invariant under T. Furthermore, the restriction of T to W rotates each vector about the origin O, and the restriction of T to U is the identity mapping of U.
Note- Observe that each vector w ¼ ða; b; 0Þ in the xy-plane W remains in W under the mapping T; hence, W is
T-invariant. Observe also that the z-axis U is invariant under T. Furthermore, the restriction of T to W rotates
Each vector about the origin O, and the restriction of T to U is the identity mapping of U.
Suppose W is an invariant subspace of T:V 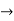 V. Then T has a block matrix representation-
V. Then T has a block matrix representation-
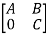
Characteristic equation:-
Let A he a square matrix, 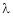 be any scalar then
be any scalar then 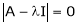 is called characteristic equation of a matrix A.
is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘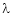 ’ be any scalar then,
’ be any scalar then,
3) 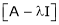 is called characteristic matrix
is called characteristic matrix
4) 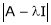 is called characteristic polynomial.
is called characteristic polynomial.
The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Cayley-Hamilton theorem
Statement-
Every square matrix satisfies its characteristic equation
That means for every square matrix of order n,
|A - 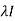 | =
| = 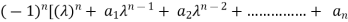
Then the matrix equation-
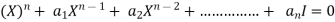
Is satisfied by X = A
That means
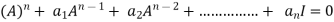
Example-1: Find the characteristic equation of the matrix A =  andVerify cayley-Hamlton theorem.
andVerify cayley-Hamlton theorem.
Sol. Characteristic equation of the matrix, we can be find as follows-
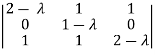
Which is,
( 2 -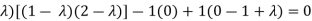 , which gives
, which gives
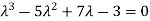
According to cayley-Hamilton theorem,
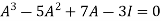 …………(1)
…………(1)
Now we will verify equation (1),
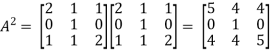
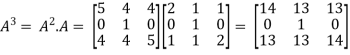
Put the required values in equation (1) , we get
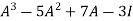
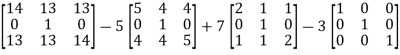
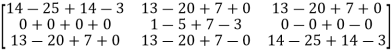
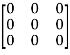
Hence the cayley-Hamilton theorem is verified.
Example-2: Find the characteristic equation of the the matrix A and verify Cayley-Hamilton theorem as well.
A = 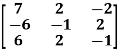
Sol. Characteristic equation will be-
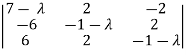 = 0
= 0
( 7 -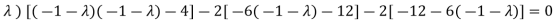
(7-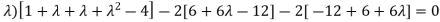
(7-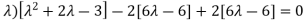
Which gives,
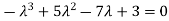
Or
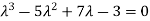
According to cayley-Hamilton theorem,
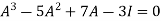 …………………….(1)
…………………….(1)
In order to verify cayley-Hamilton theorem, we will find the values of 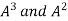
So that,
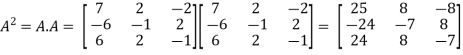
Now
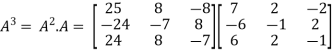
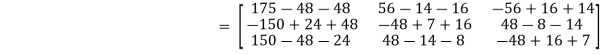
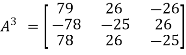
Put these values in equation(1), we get
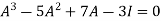
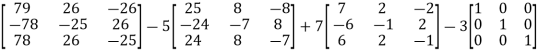 = 0
= 0
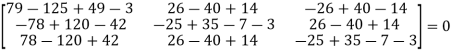

Hence the cayley-hamilton theorem is verified.
Example-3: Using Cayley-Hamilton theorem, find 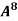 , if A =
, if A = 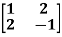 ?
?
Sol. Let A =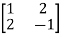
The characteristics equation of A is 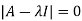
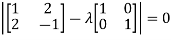
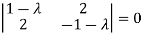
Or 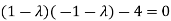
Or 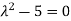
By Cayley-Hamilton theorem 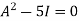
L.H.S. 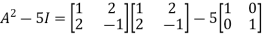
=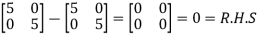
By Cayley-Hamilton theorem we have 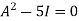
Multiply both side by 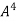
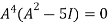 .
.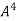
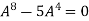
Or 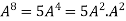
=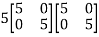
=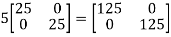
Key takeaways:
- Let T:V
 V be linear. A subspace W of V is said to be invariant under T or T-invariant if T maps W into itself
V be linear. A subspace W of V is said to be invariant under T or T-invariant if T maps W into itself - Let A he a square matrix,
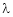 be any scalar then
be any scalar then 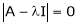 is called characteristic equation of a matrix A.
is called characteristic equation of a matrix A. - Cayley-Hamilton theorem- Every square matrix satisfies its characteristic equation
What is minimal polynomial?
Suppose A be any square matrix, Let J(A) denote the collection of all polynomials f(t) for which A is a root— that is, for which f(A) = 0. The set J(A) is not empty, by the Cayley–Hamilton theorem that the characteristic polynomial of A belongs to J(A). Let m(t) denote the monic polynomial of lowest degree in J(A). (Such a polynomial m(t) exists and is unique.) We call m(t) the minimal polynomial of the matrix A.
Note-
- The minimal polynomial m(t) of a matrix (linear operator) A divides every polynomial that has A as a zero. In particular, m(t) divides the characteristic polynomial of A.
- The characteristic polynomial and the minimal polynomial m(t) of a matrix A have the same irreducible factors
Minimal Polynomial of a Linear Operator
The minimal polynomial m(t) of a linear operator T is defined to be the monic polynomial of lowest degree for which T is a root. However, for any polynomial f ðtÞ, we have
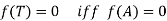
Where A is any matrix representation of T. Accordingly, T and A have the same minimal polynomials.
Thus, the above theorems on the minimal polynomial of a matrix also hold for the minimal polynomial of a linear operator.
Note-
- The minimal polynomial m(t) of a linear operator T divides every polynomial that has T as a root. In particular, m(t) divides the characteristic polynomial of T.
- The characteristic and minimal polynomials of a linear operator T have the same irreducible factors.
- A scalar
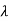 is an eigenvalue of a linear operator T if and only if
is an eigenvalue of a linear operator T if and only if 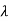 is a root of the minimal polynomial m(t) of T
is a root of the minimal polynomial m(t) of T
Example: Let 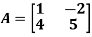 , find f(A), where
, find f(A), where
Sol:
First we will find-
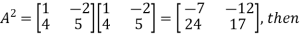
Example: Find the characteristic polynomial 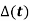 of the following matrices.
of the following matrices.
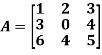
Sol:
Using the formula,
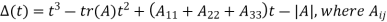 is the cofactor of
is the cofactor of 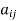 in the matrix A =
in the matrix A = 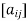
Tr(A) = 1 + 0 + 5 = 6
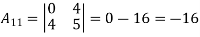
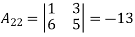
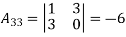

Thus
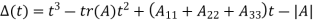
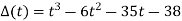
Key takeaways:
- The characteristic polynomial and the minimal polynomial m(t) of a matrix A have the same irreducible factors
- The minimal polynomial m(t) of a linear operator T divides every polynomial that has T as a root. In particular, m(t) divides the characteristic polynomial of T.
- A scalar
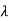 is an eigenvalue of a linear operator T if and only if
is an eigenvalue of a linear operator T if and only if 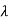 is a root of the minimal polynomial m(t) of T
is a root of the minimal polynomial m(t) of T
Definition: Let V be a vector space over F. An inner product on V is a function that assigns, to every ordered pair of vectors x and y in V, a scalar in F, denoted 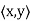 , such that for all x, y, and z in V and all c in F, the following hold:
, such that for all x, y, and z in V and all c in F, the following hold:
(a) 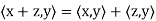
(b) 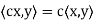
(c) 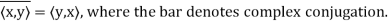
(d) 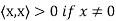
Note that (c) reduces to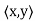 =
= 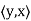 if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
It is easily shown that if 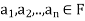 and
and 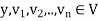 , then
, then
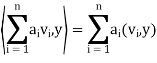
Example: For x = (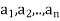 ) and y = (
) and y = (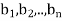 ) in
) in 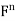 , define
, define
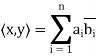
The verification that  satisfies conditions (a) through (d) is easy. For example, if z = (
satisfies conditions (a) through (d) is easy. For example, if z = ( ) we have for (a)
) we have for (a)
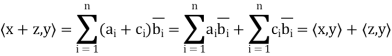
Thus, for x = (1+i, 4) and y = (2 − 3i,4 + 5i) in 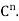
A vector space V over F endowed with a specific inner product is called an inner product space. If F = C, we call V a complex inner product It is clear that if V has an inner product 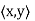 and W is a subspace of
and W is a subspace of
V, then W is also an inner product space when the same function 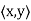 is
is
Restricted to the vectors x, y ∈ W.space, whereas if F = R, we call V a real inner product space.
Theorem: Let V be an inner product space. Then for x, y, z ∈ V and c ∈ F, the following statements are true.
(a) 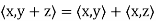
(b) 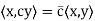
(c) 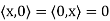
(d) 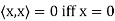
(e) If 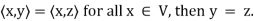
Norms:
Let V be an inner product space. For x ∈ V, we define the norm or length of x by ||x|| = 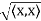
Key takeaways:
- Let V be a vector space over F. An inner product on V is a function that assigns, to every ordered pair of vectors x and y in V
Suppose {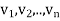 } is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {
} is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {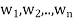 } of V as follows. Set
} of V as follows. Set
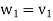
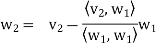
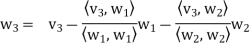
………………
……………….
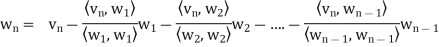
In other words, for k = 2, 3, . . . , n, we define
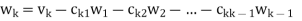
Where
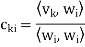
Is the component of 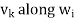 .
.
Each 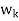 is orthogonal to the preceding w’s. Thus,
is orthogonal to the preceding w’s. Thus,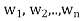 form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
The above process is known as the Gram–Schmidt orthogonalization process.
Note-
- Each vector wk is a linear combination of
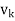 and the preceding w’s. Hence, one can easily show, by induction, that each
and the preceding w’s. Hence, one can easily show, by induction, that each 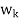 is a linear combination of
is a linear combination of 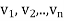
- Because taking multiples of vectors does not affect orthogonality, it may be simpler in hand calculations to clear fractions in any new
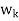 , by multiplying
, by multiplying 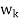 by an appropriate scalar, before obtaining the next
by an appropriate scalar, before obtaining the next 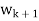 .
.
Theorem: Let 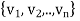 be any basis of an inner product space V. Then there exists an orthonormal basis
be any basis of an inner product space V. Then there exists an orthonormal basis 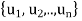 of V such that the change-of-basis matrix from {
of V such that the change-of-basis matrix from {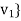 to {
to {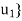 is triangular; that is, for k = 1; . . . ; n,
is triangular; that is, for k = 1; . . . ; n,
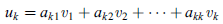
Theorem: Suppose S = 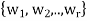 is an orthogonal basis for a subspace W of a vector space V. Then one may extend S to an orthogonal basis for V; that is, one may find vectors
is an orthogonal basis for a subspace W of a vector space V. Then one may extend S to an orthogonal basis for V; that is, one may find vectors 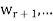 ,
,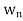 such that
such that 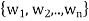 is an orthogonal basis for V.
is an orthogonal basis for V.
Example: Apply the Gram–Schmidt orthogonalization process to find an orthogonal basis and then an orthonormal basis for the subspace U of 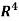 spanned by
spanned by
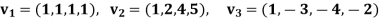
Sol:
Step-1: First 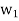 =
= 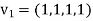
Step-2: Compute
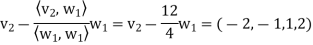
Now set- 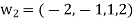
Step-3: Compute
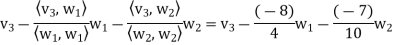
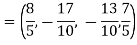
Clear fractions to obtain, 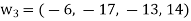
Thus, 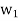 ,
, 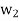 ,
, 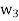 form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
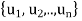 of U. We have
of U. We have
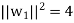
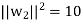
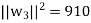
So
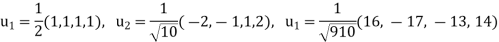
References:
1. Rao A R and Bhim Sankaram Linear Algebra Hindustan Publishing house.
2.Gilbert Strang, Linear Algebra and its Applications, Thomson, 2007.
3. Stephen H. Friedberg, Arnold J. Insel, Lawrence E. Spence, Linear Algebra (4th Edition), Pearson, 2018.
4. Linear Algebra, Seymour Lipschutz, Marc Lars Lipson, Schaum’s Outline Series