Unit - 3
Systems of variable composition
Partial molar quantities
The symbol Xi, here X refers to the extensive property present in a homogenous mixture, the principal species of the mixture is denoted by i, and forms the partial molar quantity of species i defined by
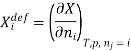
This forms the rate where the extensive property X undergoes a change with the constituent species that is added to the mixture, however the temperature pressure and the amounts of other species is kept constant. As the temperature, the pressure, and the amounts of all other species are kept constant. The partial molar quantity refers to an intensive state function whose values depend on temperature, pressure and composition of the mixture.
Here it should be noted that a charged species like ions, cannot be added directly by itself as it would result in a huge electric charge. Therefore, if the species i is charged, xi as defined by a theoretical concept whose value cannot be determined experimentally.
Among the other thermodynamic variables, the Partial molar quantities is expressed as a function. As temperature and pressure are easily controlled the functions that relate to partial molar quantities are specifically used to show in detail the chemical changes that occur in systems that refer to the assumptions and is introduced in §1. The parameter chemical potential is similar to partial molar Gibbs free energy, it plays a very important role in such equations.
Most often the pressure, temperature and the number of moles for every component are independent variables. And are useful easy to control in typical lab experiments. The Partial derivatives of thermodynamic quantities, taken with respect to the number of moles of a component, at constant pressure, temperature, and θk, are given a special designation; they are called partial molar quantities. That is,
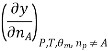
Is the partial molar energy of component A,
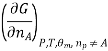
Is the partial molar Gibbs free energy, etc. All partial molar quantities are intensive variables.
The variable partial molar quantities are specifically useful; therefore, they have a distinctive symbol to represent them. We use a horizontal bar over a thermodynamic variable to represent a partial molar quantity. (A horizontal bar is used to imply per mole, when this is used to designate partial molar quantity, it implies per mole of a specific component) Thus, we write
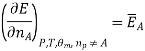

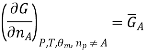
We introduce the chemical potential for substance A, μA, and find that the chemical potential of substance A is equivalently expressed by several partial derivatives. In particular, we have
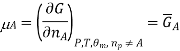

That is, the chemical potential is also the partial molar Gibbs free energy.
Using the appropriate sets of independent variables, we can obtain similar expressions for dH, dA, dG, and dS under the conditions, since entropy and pressure are the natural variables for enthalpy in a closed system, we infer that a change in the enthalpy of any system can be expressed as a function of dS, dP, changes in the non-pressure–volume work variables, dθk, and changes in the composition, dnj. That is, from
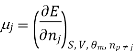
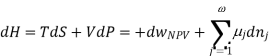
From 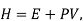 we have
we have
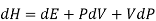
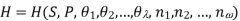
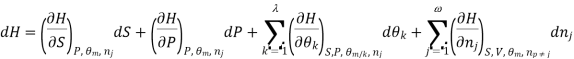
Since we assume that both these equations for dH, describe open systems, all of the variables are independent, and the corresponding coefficients are equal, for systems that satisfy our assumptions, we have
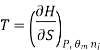
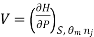
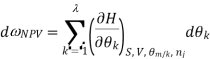

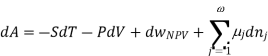
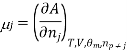
The Gibbs-Duhem equation in thermodynamics, shows the relationship between changes in chemical potential for components in a thermodynamic system.
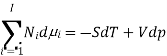
Where  represents the number of moles of the particular component,
represents the number of moles of the particular component, 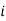 ,
,  the incremental increase in chemical potential for this component, S refers to the entropy, T the absolute temperature, V volume and p the pressure. Thermodynamically the intensive properties are not independent, they are however related forming a statement mathematically of the state postulate. When the variables are temperature and pressure, only
the incremental increase in chemical potential for this component, S refers to the entropy, T the absolute temperature, V volume and p the pressure. Thermodynamically the intensive properties are not independent, they are however related forming a statement mathematically of the state postulate. When the variables are temperature and pressure, only 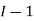 of
of 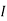 components have independent values for chemical potential and Gibb’s phase rule follows. The equation is named after Josiah Gibbs and Pierre Duhem.
components have independent values for chemical potential and Gibb’s phase rule follows. The equation is named after Josiah Gibbs and Pierre Duhem.
Derivation
The derivation of Gibbs -Duhem equation is straight forward as it is obtained from basic thermodynamic state equation. The total differential of the Gibbs free energy G in terms of its Natural variables is

With the substitution of two of the Maxell relations and the definition of chemical potential, this is transformed into:
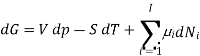
As shown in the Gibbs free energy, the chemical potential is just another name for the partial molar (or just partial, depending on the units of N) Gibbs free energy, thus
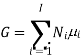
The total differential of this expression is
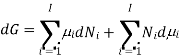
Subtracting the two expressions for the total differential of the Gibbs free energy gives the Gibbs-Duhem relation:
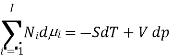
When extensive property of a solution is given by;

The change in extensive property with composition was;
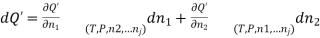 (1)
(1)
Combination of equations (1) and (2) yields;
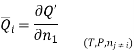
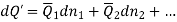
But 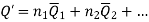
Differentiation of Equation gives
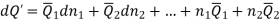
Subtracting the 3 and 5 equation we get
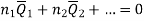
In general
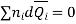
Dividing by n, total number of moles of all the components, gives
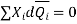
The Gibbs-duhem expression is given in the above equation.
Similarly as the partial molar volume is defined the partial molar Gibbs function for the compound I in a mixture is defined by
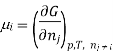
There is a specific importance for this partial molar function and is therefore called chemical potential. This potential specifies the change in gibbs function occurs as the change in the composition of the mixture also changes. Therefore as the systems try to search a minimum of the average gibbs function and will point to the direction in which the system can move so as to reducethe fuction of gibbs function, in other words the toral change in gibbs function And (dG) can be calculated from
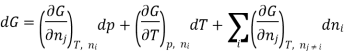
Or, by substituting the definition for the chemical potential, and evaluating the pressure and temperature:
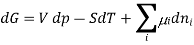
Chemical potential can be defined as the partial molar derivative any of the four
Major thermodynamic functions
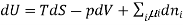
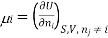

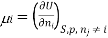
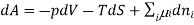
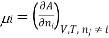

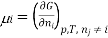
The chemical potential refers to the partial molar derivative of any four important thermodynamic functions, namely U, H, A, or G:
The commonly used definition with respect to chemical potential is defined as the partial molar Gibbs function. The definition is also very the useful,the partial Gibbs function is given by
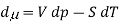
Where V is the molar volume, and SS is the molar entropy. Using this expression, it is easy to show that
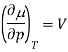
And so at constant temperature
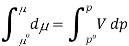
The molar volume is slightly independent of pressure and at constant temperature. (i. e., κTκT is very small), therefore Equation becomes
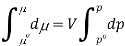
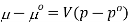

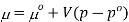
Where po is a reference pressure (generally the standard pressure of 1 atm) and μo is the chemical potential at the standard pressure. If the substance is highly compressible (such as a gas) the pressure dependence of the molar volume is needed to complete the integral. If the substance is an ideal gas
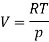
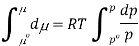
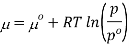
At constant temperature
Applications
In general, when we normalize the above equation, for example the total number of moles, the Gibbs-Duhem equation shows a relation between the intensive variables of the system for a simple system with 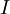 different components, there will be
different components, there will be  independent parameters or "degrees of freedom". For example, a gas cylinder filled with nitrogen is at room temperature (298 K) and at 2500 psi, the gas density, entropy or any other intensive thermodynamic variable can be determined. Therefore, If the cylinder contains a nitrogen/oxygen mixture, we need an additional piece of information, usually the ratio of oxygen-to-nitrogen.
independent parameters or "degrees of freedom". For example, a gas cylinder filled with nitrogen is at room temperature (298 K) and at 2500 psi, the gas density, entropy or any other intensive thermodynamic variable can be determined. Therefore, If the cylinder contains a nitrogen/oxygen mixture, we need an additional piece of information, usually the ratio of oxygen-to-nitrogen.
The chemical potential is defined in terms of the entropy a
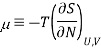
This definition leads to a general thermodynamic identity
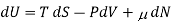
For a mixture of ideal gases, each species i constitutes a molar fraction xi of the total number N total of molecules, so each species has its own chemical potential defined as

(3) where all Nj with j 6= i are held constant in the derivative. Also, for an ideal gas, each species contributes its own portion of the overall entropy, independently of the other species. We can see this by noting that if we have a mixture of, say, 2 gases, then for each configuration of the gas A molecules there is a multiplicity of ΩB of the gas B molecules and since for an ideal gas, the molecules don’t interact, the total multiplicity of the mixture is Ωtotal = ΩAΩB, so the entropy is the sum of the entropies for the separate species: Stotal = k lnΩtotal = SA +SB. Since ideal gas molecules don’t interact, species i contributes a fraction xi of the total pressure, or in other words, its partial pressure is
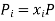
We can therefore write the thermodynamic identity for a mixture of ideal gases as

Since dSj6=i = 0 in 3 (because only the number Ni of species i is changing, and no properties of any of the other species are changing), we can write the chemical potential of species i as
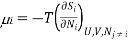
But this is the definition of chemical potential in a system containing only species i at partial pressure Pi in volume V . Thus, for a mixture of ideal gases, the chemical potential of each species is independent of the other species. In a mixture of real gases, however, this is probably not the case, since interactions between the species means.
In a single phase, two or more components mix homogenously, forming a solution. A solution is created when two or more components mix homogeneously to form a single phase. And chemical processes, occur in multiple component system, therefore such solution becomes very important, the integral part of any system is to analyse and understand the behaviour of mixtures that involve ideal and non-ideal solutions as they provide valuable information on the molecular properties of the systems.
At standard temperature and pressure, most of the gases behave like ideal gases, this enables us to combine the knowledge about ideal systems and solutions with standard state thermodynamics. in order to derive a set of equations that quantitatively describe the effect that mixing has on a given gas-phase solution’s thermodynamic quantities.
Gibbs Free Energy of Mixing
The one-component system, possess extensive properties that are dependent on the amount of the system present, however the extensive properties of a solution is dependent on the parameters such as pressure , temperature and composition, which is to be understood that the mixture is described in terms of the partial molar quantities and its components. The total Gibbs free energy of a two-component solution is given by the expression
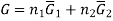
Where
G is the total Gibbs energy of the system,
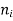 is the number of moles of component i, and
is the number of moles of component i, and  is the partial molar gibbs energy of component i.
is the partial molar gibbs energy of component i.
The molar Gibbs energy of an ideal gas can be found using the equation
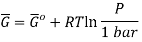
Where 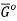 is the standard molar gibbs energy of shte gas at 1 bar and P is the pressure of shte system. In a mixture of ideal gases, molar Gibbs energy is equivalent ot its chemical potential or that
is the standard molar gibbs energy of shte gas at 1 bar and P is the pressure of shte system. In a mixture of ideal gases, molar Gibbs energy is equivalent ot its chemical potential or that
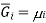
This means that a solution for ideal gases, the equation becomes,
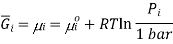
Where
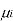 is the chemical potential of the ith component
is the chemical potential of the ith component
 is the standard chemical potential of component
is the standard chemical potential of component 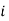 at 1 bar, and
at 1 bar, and
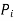 is the partial pressure of component
is the partial pressure of component 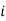 .
.
Now if we consider the two gases at the same temperature, for example gas1 and gas 2, the Gibbs free energy of the system before the gases are mixed and can be combined with the first and the above equation to form,
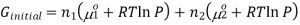
If gas 1 and 2 are mixed together, they will exert a partial pressure on the total system, P1 and P2 therefore P1+P2 = P, thus the final Gibbs free energy can be calculated using the equation,
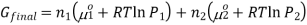
The gibbs energy of mixing,  can then be found by subtracting
can then be found by subtracting 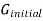 from
from 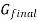 .
.
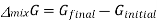
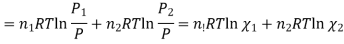
Where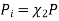
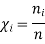
And χi is the mole fraction of gas i. This equation can be simplified further by knowing that the mole fraction of a component is equal to the number of moles of that component over the total moles of the system, o
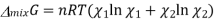
Entropy of mixing
It was Introduced by the German Physicist Rudolf Clausius in 1850, and is a highlight of 19th century Physics. The word “entropy” is derived from the Greek word, which means “turning”. It was derived to provide a quantitative measure for the spontaneous changes and Clausius introduced the concept of entropy as a precise way of expressing the Second Law of Thermodynamics, Clausius form of the second law states that spontaneous change for an irreversible process in an isolated system is a measure of randomness or irregularity or disorder of the system, the more or the randomness, higher is the entropy.
Solid state has the lowest or least entropy, the gaseous state has the highest entropy and the liquid state has the entropy that lies between the two.
Entropy is a state function. The changes in its value during any process, is called the entropy change.
ΔS = S2 -S1 = ∑S products – ∑S reactants
1) When a system absorbs heat, the molecules begin to move faster because the kinetic energy increases. Therefore, disorder increases. Greater the heat absorbed, greater will be the disorder.
2) For equal amount of heat absorbed at low temperature, the disorder will be more than at high temperature. This proves that entropy change is inversely proportional to temperature.
ΔS = eve / T
Entropy change during a process is defined as the quantity of heat (q) absorbed isothermally and reversibly divided by the absolute Temperature (T) at which the heat is absorbed.
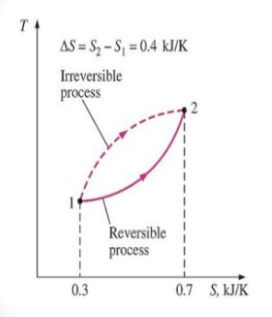
The entropy change between two specified states is the same whether the process is reversible or irreversible.
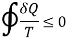
The inequity of the Clausius is a consequence of second law of thermodynamics
Q is he transfer of heat to and from the system
T is the absolute temperature at the boundary, the symbol 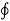 is the cyclic integral.
is the cyclic integral.
The Clausius inequality for a closed system states that the process is irreversible if TdS > dQ, and the process is reversible if TdS = dQ.
The entropy difference between any two states of a system they can be evaluated by the integral of its initial state and final state
Since entropy is a state function, the entropy change of the system for an irreversible path is the same as for a reversible path between the same two states.
For the reversible process the universe is brought back to its initial state without changing its properties. So, the entropy generation for the reversible process is zero. However, for the irreversible process, because of the disorder of the system some entropy is generated. The generated entropy is measure of the irreversibility. As a result of this the cyclic integral of the irreversible process is always less than zero.
The figure below shows that when two gases mix, it can really be seen as two gases expanding into twice their original volume. This greatly increases the number of available microstates, and therefore we can expect the entropy of the system to increase as well.
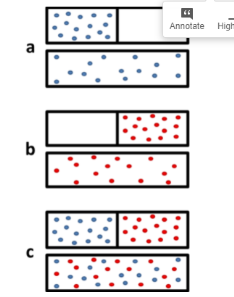
Figure: The mixing of two gases can be seen as two expansions. (a) Expansion of gas 1 alone when the barrier is removed. In the microstate of the open boxes the molecules are present in twice its number. (b) Expansion of gas 2 along. (c) The expansion of gases occur and is equivalent to mixing
In Thermodynamic the dependence of Gibbs free energy with respect to temperature is shown as
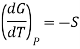
This means that differentiating Equation at constant pressure with respect to temperature will give an expression for the effect that mixing has on the entropy of a solution. We see that

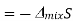
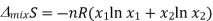
Since the mole fractions again lead to negative values for ln x1 and ln x2, the negative sign in front of the equation makes ΔmixS positive, as expected. This agrees with the idea that mixing is a spontaneous process.
A gas usually flows into a new available volume, as the molecules vigorously bounce off one another and also hit the wall of the container and moves readily into a space. According to the second law of thermodynamics, the direction of the process occurs towards the direction of a more probable state, in entropy this is expressed as a system that goes from a lesser probability (less microstates) to a state of high probability (more microstates). This corresponds to increasing the W in the equation
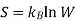
For our example, we shall again consider a simple system of two ideal gases, A and B, with a number of moles nA and nB, at a certain constant temperature and pressure in volumes of VA and VB, as shown in Figure 1A. A partition separates the two gases so that each are sequestered in their respective volume. However, if the partition is removed, we expect the two gases to randomly diffuse and form a homogenous mixture as we see in Figure B.
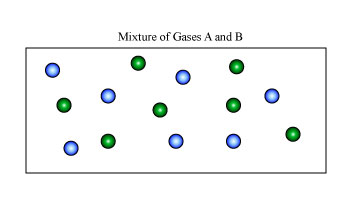
Figure: (Left) Two Gases A and B in their respective volumes and (right) A homogenous mixture of gases A and B
To calculate the entropy change, let us treat this mixing as two separate gas expansions, one for gas A and another for B. From the statistical definition of entropy, we know that
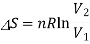
Now, for each gas, the volume V1 is the initial volume of the gas, and V2 is the final volume, which is both the gases combined, VA+VB. So, for the two separate gas expansions,
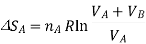
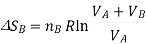
The total entropy change for both these processes is determined, as tey occur at the same time, we simply add the two changes in entropy together
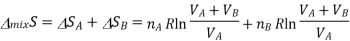
According to the ideal gas law PV=nRT, according to avagadro law the volume is directly propotionl to the number of moles, as we already are aware of the number of moles it can be substituted for volume.
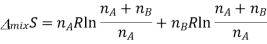
Since 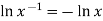 from the rules for logarithms, if we now factor out R from each term:
from the rules for logarithms, if we now factor out R from each term:
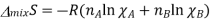
This equation is also written in number of moles and represents the equation for mixing of entropy change.
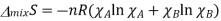
Where the total number of moles is n=nA+nB
The mole fraction of gases will be less than one when two gases are mixed together, forming a negative parentheses inside. Therefore the entropy of mixing will always be positive. For a two component solution when one component is added to another, the other component mole fraction will decrease and the log of ant less number than 1 will be negative, a positive quantity is obtained when the negative is multiplied, this equation applies to both ideal gases and ideal solutions.
Enthalpy of mixing
ΔH, or the enthalpy change is used as a unit to measure and calculate the change in energy of the system, when the need arises or if difficulty is faced In calculating energy of the system and by simultaneously ensure the amount of heat and amount of work exchanged at constant pressure and the change in enthalpy can be measured as:
ΔH=q(1)
The notation ΔHº or ΔHºrxn then arises to explain the precise temperature and pressure of the heat of reaction ΔH. The standard enthalpy of reaction is symbolized by ΔHº or ΔHºrxn and can take on both positive and negative values. The units for ΔHº are kiloJoules per mole, or kj/mol.
ΔH and ΔHºrxn
- Δ = represents the change in the enthalpy; (ΔHproducts -ΔHreactants)
- a positive value indicates the products have greater enthalpy, or that it is an endothermic reaction (heat is required)
- a negative value indicates the reactants have greater enthalpy, or that it is an exothermic reaction (heat is produced)
- º = signifies that the reaction is a standard enthalpy change, and occurs at a pre-set pressure/temperature
- Rxn = indicates that this change is the enthalpy of reaction
Standard state : The normal state of a solid or a liquid is the pure substance at a pressure of 1 bar (105 Pa) and a corresponding temperature.
The ΔHºrxn is the standard enthalpy of a reaction or the standard enthalpy of a reaction and, like ΔH, also measures the reaction enthalpy. However, ΔH ° rxn takes place under "standard" conditions, standard conditions take place at 25 ° C and 1 atm. The advantage of measuring ΔH under standard conditions is the ability to relate one ΔH ° value to another, since they occur under the same conditions.
How to Calculate ΔH Experimentally
The Enhalpy can be measured experimentally with a calorimeter. A calorimeter is an isolated system with constant pressure, i.e. ΔH = q=cpsp x m x (ΔT)

How to calculate ΔH Numerically
To calculate the standard enthalpy of reaction, the standard enthalpy of formation must be used. Another more detailed form of the standard enthalpy of reaction involves the use of the standard enthalpy of formation ΔHºf:
ΔH⊖=∑ΔvpΔH⊖f(products)−∑ΔvrΔH⊖f(reactants)
With
- vp= stoichiometric coefficient of the product from the balanced reaction
- vr= stoichiometric coefficient of the reactants from the balanced reaction
- ΔHºf= standard enthalpy of formation for the reactants or the products
Since enthalpy is a state function, the heat of reaction depends only on the final and initial states, not on the path that the reaction takes. For example, the reaction A→BA→B goes through intermediate steps (i.e. C→DC→D), but A and B remain intact.
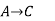
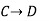
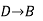
Therefore, reaction enthalpy can be measured as the sum of them? H The three reactions by the application of the law
Hess, of ΔH ° represents the total energy change in the reaction of this value can be positive or negative.
• A positive value means a ΔH state addition of energy from the reaction (and surrounding), resulting in an endothermic reaction.
• A negative value for ΔH ° represents a power removal of the reaction (and in the environment), and so the reaction is exothermic.
Example: the combustion of acetylene
Calculate the enthalpy change for the combustion of acetylene (C2H2C2H2)
Solution
1) The first step is to ensure that the equation is compensated and Correct. Remember, the combustion of a hydrocarbon - Oxygen requires and results in the production of carbon dioxide and water.
2C2H2(g)+5O2(g)⟶4CO2(g)+2H2O(g)(3)(3)2C2H2(g)+5O2(g)⟶4CO2(g)+2H2O(g)
2) Below, Locate a standard training enthalpy table can be found the values of the reaction components.
3) First locate the enthalpies of the products:
ΔHºf CO2 = -393.5 kJ/mole
Multiply this value by the stoichiometric coefficient, which in this case is corresponds to 4 moles
vpΔHºf CO2 = 4 mol (-393.5 kJ/mole)
= -1574 kJ
ΔHºf H2O = -241.8 kJ/mole
The stoichiometric coefficient of this compound is upto to 2 mole. So,
vpΔHºf H2O = 2 mol ( -241.8 kJ/mole)
= -483.6 kJ
Now add these two values in order to get the sum of the products
Sum of products (Σ vpΔHºf(products)) = (-1574 kJ) + (-483.6 kJ) = -2057.6 kJ
Now, find the enthalpies of the reactants:
ΔHºf C2H2 = +227 kJ/mole
Multiply this value by the stoichiometric coefficient, which in this case is upto to 2 mole.
vpΔHºf C2H2 = 2 mol (+227 kJ/mole)
= +454 kJ
ΔHºf O2 = 0.00 kJ/mole
The stoichiometric coefficient of this compound is equal to 5 mole. So,
vpΔHºf O2 = 5 mol ( 0.00 kJ/mole)
= 0.00 kJ
Add these two values in order to get the sum of the reactants
Sum of reactants (Δ vrΔHºf(reactants)) = (+454 kJ) + (0.00 kJ) = +454 kJ
The sum of the reactants and products can now be inserted into the formula:
ΔHº = Δ vpΔHºf(products) - ? vrΔHºf(reactants)
= -2057.6 kJ - +454 kJ
= -2511.6 kJ
Reaction enthalpy
During any chemical reaction, heat is either absorbed or given out. The heat exchange between the chemical reaction and its environment is reaction enthalpy (H). This cannot be measured directly. For this, there is a measurement of change in the temperature of a reaction over time to the final change in enthalpy denoted by ΔH.
From the value of ΔH, whether in a reaction heat is absorbed from the environment [endothermic] or is given off to the environment [exothermic] is determined. In general, ΔH is given as, ΔH = m×s×ΔT, where m is the mass of reactants, s is the specific heat of products, and ΔT is a change in temperature during the completion of the reaction.


How to Calculate the Reaction Enthalpy?
To find enthalpy of a chemical reaction we need to follow the below mentioned steps.
- Determine products and reactants of the reaction
- Find total mass of reactants
- Determine the specific heat values of the products
- Find the difference in temperature between the start and end of a reaction
- Finally, multiply the mass of reactants by the heat values and that number, in turn, by the change in temperature
Finally, we will get the enthalpy of the chemical reaction.
Example of Enthalpy Calculation
Hydrogen reacts with oxygen to give water. The chemical reaction is,
2H2 + O2 → 2H2O
Reactants Products
- Step 1: Determining reactants and products – In this reaction, H2 and O2 are the reactants and H2O is the products.
- Step 2: Determination of the total mass of reactants – We can find total mass of reactants from the molar masses which can be formed in the periodic table
- 2H2 + O2 = 2H2O
2×[2g] 1×[32g] = 4g + 32g =36g
- Step 3: Determining specific heat of products – Every product has a specific heat value associated with it, which are constant values. Specific heat values carry the unit joule/gram°C.
2H2 + O2 = H2O
The specific heat of water is 4.2 joule/gram°C
- Step 4: Finding the difference in temperature after completion of reaction – For this, we have to subtract initial temperature (T1) of the reaction from the final temperature (T2) of the reaction, expressed in Kelvin.
ΔT = T1 – T2 (T1 = 185K and T2 = 95 K) = 185K – 95K
ΔT = -90K
In the above reaction, the reactants had more temperature, and after the completion of the reaction, the product got cooled off.
- Step 5: Use of formula ΔH = m×s×ΔT
ΔH = 36g×42 jg-1k-1 ×(-90)K = -13608 joule
ΔH < 0
- Step 6: Determining whether this reaction gained or lost energy – ΔH determines whether the reaction gains or loses heat. The positive sign of ΔH means, the reaction gains heat and hence is endothermic. If the sign of ΔH is negative, the reaction is exothermic.
This makes logical sense since hot gases hydrogen (H2) and oxygen(O2) react together and let off heat to the environment. Then water [H2O] forms, indicating that it is an exothermic reaction.
Which other methods are used to calculate enthalpy?
Here is the alternate method
- Use of bond energies: Chemical reactions involve making and breaking of chemical bonds. If we know the energy required to make or break the bonds in the reaction, then we can calculate the enthalpy change for the entire reaction. For example, hydrogen and fluorine react together to give hydrogen fluoride.
H2 + F2 → 2HF
We need bond energy to break H2 and F2 molecules of 436kJ/mol and 158kL/mol, respectively. The bond energy required to form HF molecule is -568kJ/mol.
H2 + F2 → 2HF
436kJ/mol 158kJ/mol 2*(-568)
= -1136 kJ/mol
Adding these values together we get,
436 + 158 + (-1136) = -542kJ/mol
Standard enthalpy changes
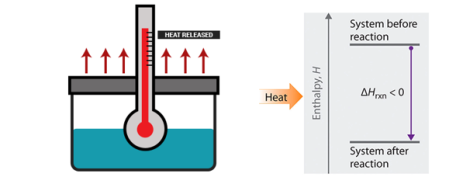
Enthalpy change: Standard Enthalpy of Reaction
When we consider a chemical reaction, an understanding of enthalpy and standard enthalpy is very important, this helps in calculating the amount of heat and cold needed when the reaction is carried out in large scale for example a large production of various components like ammonia, oxygen, calcium carbonate etc
We know that in an ideal system ΔG=ΔH−TΔSΔG=ΔH−TΔS, but this equation can also be applied to the thermodynamics of mixing and solved for the enthalpy of mixing so that it reads
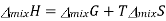
Plugging in our expressions for ΔmixG and ΔmixS , we get
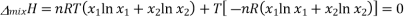
This result makes sense when considering the system. The molecules of ideal gas are spread out enough that they do not interact with one another when mixed, which implies that no heat is absorbed or produced and results in a Δmix of zero. Figure illustrates how TΔmix and Δmix change as a function of the mole fraction so that ΔmixH of a solution will always be equal to zero (this is for the mixing of two ideal gasses).
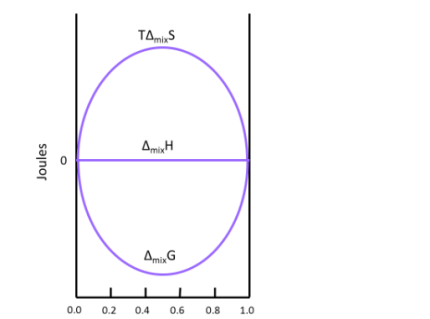
A graph of 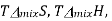 and
and 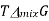 as a function of
as a function of  For the mixing of two ideal gases.
For the mixing of two ideal gases.
Thermodynamic equilibrium is a self-evident and clear concept of thermodynamics, it is a single system and an internal state thermodynamic system.it also refers to the various other thermodynamic systems that are connected more or less to the permeable and impermeable walls. In thermodynamic equilibrium there are no macroscopic net flows of matter or energy within a system or between systems.
No macroscopic change occurs when a system is in its own internal thermodynamic equilibrium state.
In thermodynamic equilibrium, systems are of a reciprocal nature and include thermal, mechanical, chemical and radiation equilibria. The system can exist in a kind of mutual equilibrium, in thermodynamic equilibrium, all kinds of equilibrium hold at once and indefinitely, until disturbed by a thermodynamic operation. In a macroscopic equilibrium, perfectly or almost perfectly balanced microscopic exchanges occur; this is the physical explanation of the notion of macroscopic equilibrium.
A spatial uniform temperature is present, when the equilibrium is in internal equilibrium thermodynamically. Apart from the temperature the intensive properties are driven by a spatial inhomogenity and also from the surrounding a long-range unchanging force field is imposed.
When a system is not in equilibrium, there is a net flow of matter and energy.in such conditions changes occur in the system, the system is said to be in a meta-stable equilibrium.
Though not a widely named "law," it is an obvious state of thermodynamics that there exist states of thermodynamic equilibrium. The second law of thermodynamics says that when a body of matter begins from a state of equilibrium, in which parts of it are kept in different states by partitions more or less permeable or impermeable, and a thermodynamic process removes or makes the partitions more permeable and isolates itself, then it spontaneously reaches its own new state of internal thermodynamic equilibrium, and this is accompanied by an increase in the sum of the entropies of the parts
Hence the concept of equilibrium something that "balances". Equilibrium is a state of vanishing driving forces or gradients in which everything is constant. When a system is in equilibrium, it maintains its current state because there are no driving forces that do not change anything.
When two materials have similar temperature, they are called thermal equilibrium. There are no thermal gradients and no exchange of heat takes place for example a liquid and a vapor phase are in thermal equilibrium when:
Tl=Tv
Mechanical equilibrium occurs when two substances are present at same pressure, there is absence of bulk movement as there is no pressure gradients. A liquid and a vapor phase are in mechanical equilibrium when:
Pl=Pv
For a system that is thermodynamic, if it has to be in equilibrium then all its intensive (temperature, pressure) and extensive thermodynamic properties (U, G, A, H, S, etc) must be constants. Therefore, the total changes that occur in any of these properties should be zero at equilibrium.
When we consider a heterogeneous vapour-liquid closed system, any change that occurs in the total property of the system, results in the change of that property in the liquid phase and also the changes of that property in the vapour phase.
DI(total)=dI(liquid)+dI(vapor)
In this case, the liquid and the vapour are not closed system themselves, however they can exchange liquid and vapour within themselves but not with the surroundings. To elaborate more upon the concept of equilibrium, let’s look at equation .as it refers to the changes in pressure and temperature, the two measurable laboratory quantities written in both phases
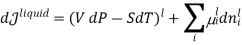
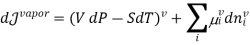
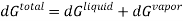
Hence
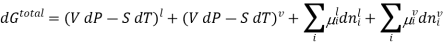
Since at equilibrium all extensive properties, such as G, must remain constant, dG(total) must be zero.
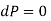 [Mechanical equilibrium]
[Mechanical equilibrium]
DT=0 [Thermal equilibrium]
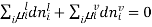 [
[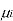 criteria for equilibrium]
criteria for equilibrium]
It can be also proven that, A minimum value of the total free energy of the system (G(total)) is attained at equilibrium, the total free energy of the system must take a minimum value; this reinforces the fact that dG(total)=0 at equilibrium. The minimum Gibbs energy criterion for equilibrium is a restatement of the second law of thermodynamics, from which we know that the entropy of a system in equilibrium must be at its maximum, considering all of the possible states for equilibrium.
The product of activities at equilibrium is known as equilibrium constant of the reaction
ΔrGo = - R T I n K
When ΔrGo > 0, K< 1
i.e at equilibrium, the partial pressure of A> partial pressure of B
PA > PB
Which means reactant A is favoured in the reaction or the reaction proceeds in the backward reaction.
When ΔrGo < 0
i.e at equilibrium, the partial pressure of b > partial pressure of A
PA < PB
Product B is favoured in the reaction and the reaction proceeds in the forward reaction.
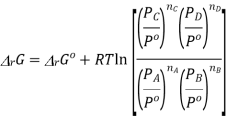
Consider a reaction of the type
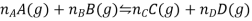
Where A, B, C, and D all behave ideally. During the reaction, the partial pressure of each gas changes. The resulting free energy change for each gas can be expressed as
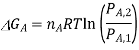
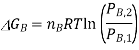
If we assume that the reaction starts with each gas at the standard pressure, denoted as P°, we may write
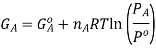
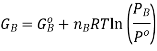
It is important to remember that the free energies in the expressions above are NOT molar quantities, ie we need to keep in mind that 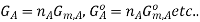 Now, the free energy change for the reaction may be written as
Now, the free energy change for the reaction may be written as
Where 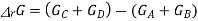
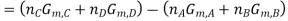
And 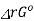 is similarly defined.
is similarly defined.
Now at equilibrium 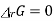
And so, we get
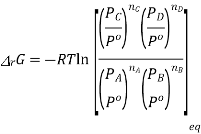
The partial pressures that enter into this expression are the values measured at equilibrium and, therefore, is a constant at a given temperature. Note that, because of the division of each pressure term by the standard pressure, the quantity within the square brackets is dimensionless
In other words,
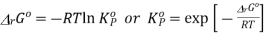
This is the thermodynamically correct definition of the equilibrium constant in relation to pressure. Note that this is a dimensionless quantity due to the division of each pressure term by the standard pressure. For real gases, the partial pressures must be replaced by partial flow capacities. The equilibrium constant can also be expressed in concentrations by inserting PA = nART / V etc. and recognizing that nA / V = [A] etc. where xA is the mole fraction of A and P is the total pressure in equilibrium, we can express the equilibrium constant in terms of mole fractions K
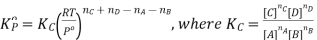
Also, by recalling that PA = xAP, where xA is the mole fraction of A and P is the total pressure at equilibrium, we can express the equilibrium constant in terms of mole-fractions K
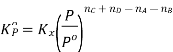
Where 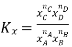
A thermodynamic process is any process in which heat energy moves within a system or between systems.
Thermodynamic properties can be divided into 2 (two) general classes, for example intensive and extensive properties.
An intense property is the physical property of the system that does not depend on the size or amount of material in the system. In contrast, the extensive property of a system does not depend on the size of the system or the amount of material. Density, pressure and temperature are by definition intensive properties and volume, internal energy are extensive properties.
Symbols for the representation of properties: Extensive properties are symbolized with capital letters (capital letters) such as V (volume), KE (kinetic energy), PE (potential energy) etc. Intensive properties are indicated with lowercase letters such as v (specific volume), ke (specific kinetic energy), e, u (specific internal energy), h (specific enthalpy) etc.
Energy or Exceptions: temperature (intensive), mass (extensive ) and number of moles (extensive). The use of symbols for temperature, mass, and mole is traditional.
Exceptions:
Symbols for exceptional properties
Parameter property Traditional symbol
Temperature-intensive property T
Mass extensive property M
Number of moles Extensive property N
Specific extensive properties, ie extensive properties per unit mass are intensive properties. For example: specific volume, specific energy, density, etc.
The four types of thermodynamic processes are isobaric, isochoric, isothermal and adiabatic.
Symbols for Exceptional Properties
Parameter | Property | Traditional symbol |
Temperature | Intensive property | T |
Mass | Extensive property | M |
Number of moles | Extensive property | N |
The Four Types of Thermodynamic Processes
The state of a given thermodynamics system can be expressed by various parameters like Pressure (P), temperature(T), volume(V) and internal energy(U), if ant two parameters are fixed, suppose pressure (P) and volume (V) of a fixed mass of gas, then the temperature (T) of the gas will be automatically fixed according to the equation PV=RT. No change can be made to T without altering P and V.
Work in Thermodynamic Processes
When the volume (V) of a system alters, it is said that pressure-volume work has occurred. A thermodynamic process occurring in a closed system in such a way that the rate of volume change is slow enough for the pressure (P) to remain constant and uniform throughout the system, is a quasi-static process. In this case, work (W) is represented as:
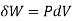 where
where 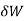 is the infinitesimal work increment by the system, and dV is the infinitesimal volume increment.
is the infinitesimal work increment by the system, and dV is the infinitesimal volume increment.
Also, 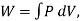 where W is the work the system does during the entire reversible process.
where W is the work the system does during the entire reversible process.
Isobaric Process
An isobaric process is one where the pressure of the system (often a gas) stays constant. "Iso" means the same thing and "baric" means pressure. The pressure is related to the force that the molecules exert on the walls of the container. Imagine you have a gas in a moving flask and you heat it. By heating the gas, you accelerate the molecules, which would normally increase the pressure, but at the same time the piston expands, increases in volume and gives the molecules more freedom of movement.Since the walls of the container are now larger, the pressure can remain the same even though the molecules move faster, so it is an isobaric process.
Since the pressure (P) is constant in this process, the volume of the system changes. The work (W) done can be calculated as W=P ( Vfinal – V initial)
If ΔV is positive (expansion), the work done is positive. For negative ΔV (contraction) the work done is negative.
Isochoric Process
An isochoric process is one where the volume of the system stays constant. Again, 'iso' means the same and 'choric' means volume. Volume is the amount of space the material takes up. So, this would be like heating a gas in a solid, non-expandable container. The molecules would move faster and the pressure would increase, but the size of the container stays the same.
The volume remains constant in an isochoric process. Therefore, the system does not do any work (since ΔU=0, PΔV or W is also zero). Such a process in which there is no change in volume can be achieved by placing a thermodynamic system in a closed container which neither contracts nor expands. Thus, from the first law of thermodynamics (Q=ΔU + W), change in internal energy becomes equal to the heat transferred (ΔU = Q) for an isochoric process.
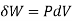 where
where 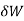 is the infinitesimal work increment by the system, and dV is the infinitesimal volume increment.
is the infinitesimal work increment by the system, and dV is the infinitesimal volume increment.
Also, 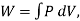 where W is the work the system does during the entire reversible process.
where W is the work the system does during the entire reversible process.
Isothermal Process
An isothermal process is a process in which the temperature of the system is kept constant. Thermal is related to heat, which in turn is related to temperature. Temperature is the average heat energy (movement) of the molecules in a substance.
An example of an isothermal process would be if we take a gas behind a moving piston and compress it: the volume has decreased and the pressure behind the piston has increased because the molecules have less room to move. You're compressing a piston, you're using energy, you're working on the gas, so normally the molecules would gain energy and move faster, and the temperature would go up. In an isothermal process, the temperature of the system remains constant.

From gas law,
PV=nRT
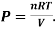 Using the value of O in the work equation
Using the value of O in the work equation
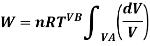
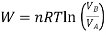
If 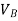 is higher than
is higher than 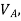 the work done will be positive or else negative.
the work done will be positive or else negative.
Since internal energy is temperature -dependent, ΔU=0 because the temperature is constant and thus from the first law of thermodynamics (Q= ΔU+W), we will get Q=W
Adiabatic process
The thermodynamic process in which there is no exchange of heat from the system to its surrounding neither during expansion nor during compression.
The adiabatic process can be either reversible or irreversible. Following are the essential conditions for the adiabatic process to take place:
- The system must be perfectly insulated from the surrounding.
- The process must be carried out quickly so that there is a sufficient amount of time for heat transfer to take place
No heat is exchanged with the system in an Adiabatic process (Q=0), its mathematical representation is
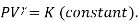
Also,  . Substituting the value of P in the work equation:
. Substituting the value of P in the work equation:

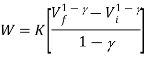
Since Q=0 for an adiabatic process, from the first law of thermodynamics (Q=ΔU+W), we will get ΔU= -W. Thus the internal energy will increase if the work done is negative and vice versa.
Adiabatically when an ideal gas is compressed, (Q=0) its temperature generally increases: when we consider an adiabatic expansion process, the ideal gas does not work and the temperature decreases, a few adiabatic compressions examples include compression occur in the cylinder of a car, where the gas-air mixture take place so quickly that there is no time for the mixture to exchange heat with its environment.
The figure below shows the adiabatic process in the free expansion of a gas, that is confined by a membrane to one side of a two-compartment that is thermally insulated container. When the membrane is punctured, the gases rushes to the other side of the container and therefore expand freely, Because the gas expands “against a vacuum” (p=0), it does no work, and because the vessel is thermally insulated, the expansion is adiabatic.
With Q=0 and W=0W=0 in the first law, ΔEint=0,ΔEint=0, so
Eint i = Eint f for free gas expansion.
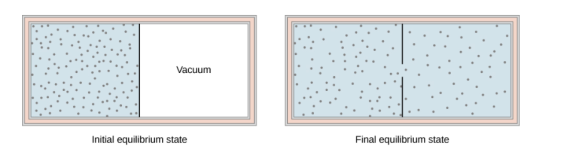
The gas in the left chamber expands freely into the right chamber when the membrane is punchured.
If the gas is ideal, the internal energy depends only on the temperature. So when an ideal gas expands freely, its temperature does not change.
Reversible adiabatic expansion of the ideal gas
In an adiabatic process, no heat enters or leaves the system, therefore the first law for a reversible adiabatic process has the form
DU = - PdV.
CV = (∂U / ∂T) V. (taking into account the molar heat capacity)
But the internal energy of an ideal gas only depends on the temperature and is independent of volume (since there are no intermolecular forces), for an ideal gas
CV = dU / dT, so we have dU = CVdT.
Therefore, for a reversible adiabatic process and an ideal gas
CVdT = −PdV. (The minus sign shows that as VT increases as expected.) But for one mole of an ideal gas,
PV = RT = (CP - CV) T or P = (CP - CV) T / V.
Hence
CvdT = - (CP - CV) TdV / V
Separate the variables and write γ for CP / CV:
Integra:
TVγ - 1 = constant.
This shows how the temperature and volume of an ideal gas change during reversible adiabatic expansion or compression. As the gas expands, the temperature drops. When the gas is compressed, it heats up. Of course, the pressure also varies and the ideal gas corresponds to the equation
PV / T = constant.Eliminating T we get
PVγ = constant
On elimination of V we obtain
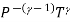 =constant
=constant
We have seen that, for a closed system, the Gibbs energy is related to pressure and temperature as follows:
DG=VdP−SdT
For a constant temperature process,
DG=VdP @ constant T
For an ideal gas,
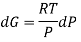
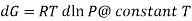
The expression is applied only to ideal gases, but later this concept was extended and the expression was applicable to all substances, this was done by Lewis in 1905 and he defined a new thermodynamic property was defined called the fugacity, f, such that:
DG=RTd In f @ constant T
This definition implies that for ideal gases, ‘f’ must be equal to ‘P’. For mixtures, this expression is written as:
DGi¯¯¯¯=RTd In fi @ constant T
Where Gi¯¯¯¯ and fi are the partial molar Gibbs energy and fugacity of the i-th component, respectively. As Gibbs energy is closely related to chemical potential, Fugacity can be related directly to chemical potential. Therefore, the definition of fugacity in terms of chemical potential becomes:
For a pure substance,
d In f=dμRT@ constant T
LimP→0 f=P (ideal gas limit)
For a component in a mixture,
d In fi= dμiRT@ constant T
LimP→0 fi=yiP = partial pressure (ideal gas limit).
The fugacity coefficient (ϕi is defined as the ratio of fugacity to its value at the ideal state. Hence, for pure substances:
ϕ=fP2
And for a component in a mixture,
ϕi=fiyiP
y coefficient takes a value of unity when the substance behaves like an ideal gas. Therefore, the fugacity coefficient is also regarded as a measure of non-ideality; the closer the value of the fugacity coefficient is to unity, the closer we are to the ideal state.
Fugacity results in a secondary chemical potential, the above definitions allow us to restate the same principle in terms of fugacity. To do this, previous expressions can be integrated for the change of state from liquid to vapor at saturation conditions to obtain:
∫lvd In fi=1RT∫lvdμi
In f(v)i− In f(v)i=1RT(μ(v)i−μ(l)i)
For equilibrium, μ(l)i=μ(v)i
Hence,
In(f(v)if(l)i)=0
Therefore:
f(l)i=f(v); i=1, 2, ... nci
The fugacities must be the same for equilibrium.in other words for the system to be in equilibrium. The chemical potential and fugacity of each component in every phase must be equal. Once one of them is satisfied, the other is satisfied immediately.
Using μ(l)i=μ(v)i or f(l)i=f(v)i
To describe equilibrium is a matter of choice, but generally the fugacity approach is preferred
The Van 't Hoff equation relates the change in the equilibrium constant, Keq, of a chemical reaction to the change in temperature T, given the standard enthalpy change, ΔrH⊖, for the process
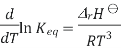
Where ln denotes natural logarithm Keq is the thermodynamic equilibrium constant, and R is the ideal gas constant. This equation is similar and occurs at all pressures and at any one temperature, it is derived from the requirement that the Gibbs free energy of reaction be stationary in a state of chemical equilibrium.
In general, the equation is integrated at two temperatures, assuming the standard reaction enthalpy ΔrH⊖ is constant (and furthermore, this is also often assumed to be equal to its value at standard temperature). Since in reality ΔrH⊖ and the standard reaction entropy ΔrS⊖ do vary with temperature for most processes, the integrated equation is only approximate. Approximations are also made in practice to the activity coefficients within the equilibrium constant.
A new equilibrium constant is established when the equation is integrated at a new absolute temperature, that assumes standard enthalpy change over the temperature range. To obtain the integrated equation, it is convenient to first rewrite the Van 't Hoff equation as
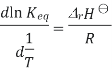
The definite integral between temperatures 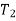 and
and 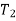 is then
is then
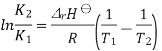
Combining the well-known formula for the Gibbs free energy of reaction
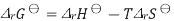
Where S is the entropy of the system, with Gibbs free energy isotherm equation

We obtain


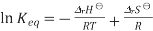
Differentiation of this expression with respect to the variable T while assuming that both ΔrH⊖ and ΔrSH⊖ are independent of T yields the Van 't Hoff equation. These assumptions are expected to break down somewhat for large temperature variations.
Provided that ΔrH⊖ and ΔrSH⊖ a are constant, the preceding equation gives ln K as a linear function of 1/T and hence is known as the linear form of the Van 't Hoff equation. Therefore, a straight line Is formed, when a plot of the natural logarithm of the equilibrium is plotted against reciprocal temperature .as the temperature is quite small and the standard Enthalpy and Entropy is constant. The slope of the line may be multiplied by the gas constant R to obtain the standard enthalpy change of the reaction, and the intercept may be multiplied by R to obtain the standard entropy change.
The Equilibrium Constant (Kc)
For a given temperature, the concentration of the reactants and products are constant at equilibrium. Considering the simple reaction that is reversible where A & B are the reactants whereas C & D are the products.
A + B ⇌ C + D
A mixture of reactant and products at a state of equilibrium is called as equilibrium mixture. There is a relationship that exists between the concentration of reactants and the concentration of products for a given equilibrium mixture. This relation can be equated as follows.
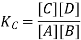
Here, Kc is called the equilibrium constant. In this equation, the concentration of A at equilibrium is shown as [A] (similarly for B, C and D), and the stoichiometric coefficients of the reactants and products have been observed experimentally that the equilibrium constant also depends on the stoichiometric coefficients of reactants and Products.
Hence, the law of mass action requires that the equilibrium constant, at a given constant temperature, is equal to the product of the concentration of the products in the respective stoichiometric coefficient increased, divided by the product of the concentrations of the reactants, which in each case increased the corresponding stoichiometric coefficient.
This is also known as the law of equilibrium or the law of chemical equilibrium
Equilibrium Constant for Homogeneous and Heterogeneous Reaction
Introduction to Homogeneous equilibrium
To simplify the problems and to understand the concept we divide such reactions into different categories, namely homogeneous reactions in which the components involved in the reaction are present in the same phase and heterogeneous reactions, in which the components involved are in different phases. The methods of treating both reactions are different and so is the determination.
Equilibrium Constant for Homogeneous Reaction
Let us consider a homogeneous system, given by the following reaction
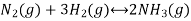
Ammonia is formed when gaseous nitrogen reacts with gaseous hydrogen, the equilibrium constant can now be calculated for the reaction above.
We can write the molar concentration of the reaction components, can be written as
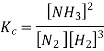
As we know, for reactions involving gases, we express the equilibrium concentration in terms of the partial pressure.
Using the ideal gas equation,
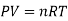
Where P is the pressure of the system, V is the volume of the system, n is the number of moles of the components in the system, R is the universal gas constant, and T is the temperature of the system.
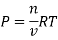
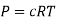
Here, c is the concentration of the system. We can also write it as,
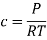
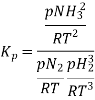
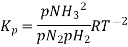
So, equilibrium constant can also be written as,
Here, we note that the general expression for Kc and Kp can be written as,
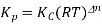
Where Δn refers to the numbers of moles of gaseous products and the number of moles of gaseous reactants.
Equilibrium Constant for Heterogeneous Reaction
When the state of equilibrium in a system has components in more than one phase, it is called heterogeneous equilibrium if, for example, we take a container of ice and water at a temperature that allows both phases to exist simultaneously, so that both ice and water. Water is in a state of equilibrium. This state is called heterogeneous equilibrium.
In his equation this can be written as follows:
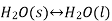
When we look at another example, an aqueous solution of a solid like calcium hydroxide, we observe that the solid calcium hydroxide is in equilibrium with its saturated solution.
Writing the equilibrium constant for heterogeneous reactions differs from that for homogeneous reactions. For example, consider the thermal dissociation of calcium carbonate into calcium oxide and carbon dioxide. Here we see that the equilibrium constant for the dissociation of the reactant into its products depends only on the gaseous component, since solid and liquid reactants are regarded as constant.
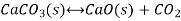
Here, the components CaCO3 and CaO are solids, so their molar concentration remains constant throughout the reaction. Therefore, the equilibrium constant can be written as,
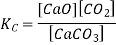
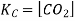
Also, in terms of Kp, we can write
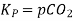
Where p denotes the partial pressure. In other words, we can state that, at a given temperature, there is a constant concentration or partial pressure of CO2 in the equilibrium reaction with CaO and CaCO3.
Gibb’s energy is a state function and an Extensive property Since, change in enthalpy too increases or decreases the randomness by affecting the molecular motions, entropy change alone cannot account for the spontaneity of such process. Therefore, we use the Gibbs energy change for explaining the spontaneity of a process
Expression for Gibbs Energy Change
General expression for Gibb’s energy change at constant temperature is expressed as:
△Gsys = △Hsys–T△Ssys
Where,
△Gsys = Gibbs energy change of the system
△Hsys = enthalpy change of the system
△Ssys = entropy change of the system
T = Temperature of the system
Above equation is popularly known as Gibbs equation. Gibbs’ equation relates enthalpy and entropy of the system. We know that for a spontaneous process, the total entropy change,
△Stotal is greater than zero.
△Stotal = △Ssys+△Ssurr
Where,
△Stotal = total entropy change for the process
△Ssys = entropy change of the system
△Ssurr = entropy change of the surrounding
In case of thermal equilibrium between system and surrounding, temperature change between system and surrounding, △T = 0. Hence, we can say that enthalpy lost by the system is gained by the surrounding. Hence, the entropy change of the surrounding is given as,
△Ssurr = △HsurrT=–△HsysT
△Stotal = △Ssys+(−△HsysT)
△Hsurr = change in enthalpy of the surrounding
△Hsys = change in enthalpy of the system
As discussed earlier, for the spontaneity of a process,
ΔStotal > 0. Above equation becomes,
T△Ssys–△Hsys>0
△Hsys–T△Ssys<0
Above equation can be related to Gibbs equation as,
△Gsys<0
On the basis of above equation we can infer:
- △Gsys<0, the process is spontaneous
- △Gsys>0, the process is non-spontaneous
The Spontaneity of a Process
Gibbs equation helps us to predict the spontaneity of reaction on the basis of enthalpy and entropy values directly. When the reaction is exothermic, enthalpy of the system is negative making Gibbs free energy negative. Hence, we can say that all exothermic reactions are spontaneous.
In the case of endothermic reaction when enthalpy of the system is positive, the process is spontaneous under two conditions:
- Temperature is very high to make the Gibbs energy value negative
- Entropy change is very high to make the Gibbs free energy negative.
Spontaneity can only indicate if a reaction can occur not necessarily if a reaction will occur. For example, the conversion of diamond to graphite is a spontaneous process at Standard Temperature and Pressure (STP) but it is a slow process. It will take years for the transformation to occur
The equilibrium constant of a chemical reaction (usually denoted by the symbol K) provides insight into the relationship between the products and reactants when a chemical reaction reaches equilibrium. For example, the equilibrium constant of concentration (denoted by Kc) of a chemical reaction at equilibrium can be defined as the ratio of the concentration of products to the concentration of the reactants, each raised to their respective stoichiometric coefficients. It is important to note that there are several different types of equilibrium constants that provide relationships between the products and the reactants of equilibrium reactions in terms of different units.
For a chemical reaction, the equilibrium constant can be defined as the ratio between the amount of reactant and the amount of product which is used to determine chemical behaviour.
At equilibrium, Rate of the forward reaction = Rate of the backward reaction
i.e. rf = rb Or, kf × α × [A]a[B]b = kb × α × [C]c [D]d
At a particular temperature, the rate constants are constant. The ratio of the rate constant of forward reaction to the rate constant of backward reaction should be a constant and is called an equilibrium constant (Kequ).
Kequ = kf/kb = [C]c [D]d/[A]a [B]b = Kc
Where Kc, indicates the equilibrium constant measured in moles per litre.
For reactions involving gases: The equilibrium constant formula, in terms of partial pressure will be:
Kequ = kf/kb = [[pC]c [pD]d]/[[pA]a [pB]b] = Kp
Where Kp indicates the equilibrium constant formula in terms of partial pressure
Larger Kc/Kp values indicate higher product formation and higher percentage conversion.
- Lower Kc/Kp values indicate lower product formation and lower percentage conversion.
- Medium Kc/Kp values indicate optimum product formation.
Relation between Kc, Kp and Kx
For a balanced reaction of the type,
AA + bB ⇌ cC + dD
According to the law of mass action, the constant value obtained by relating equilibrium concentrations of reactants and products is called the equilibrium constant. For the forward reaction, this is given by
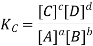
The equilibrium constant for the reverse reaction is the inverse of the forward reaction and is given by:
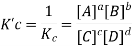
If the coefficients of the chemical equation are multiplied by a factor ‘n’ then the equilibrium constant is raised by the power ‘n’ i.e., the constant becomes Knc.
Equilibrium Constant Representation | Expressed in terms of | Expressed as |
Kc | Concentrations of reactants and products | 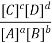 |
Kp | Partial pressures of reactants and products. (only for the substances which are in gaseous state) | 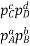 |
Kx | Mole fractions of reactants and products | 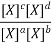 |
Relation between Kc, Kp and Kx
Kp = Kc(RT)Δng
Kx = Kp(RT)Δng
Where,
Δng = moles of gaseous products – moles of gaseous reactants.
Kc is the equilibrium constant expressed in terms of the concentration of the reactants/products. Similarly, Kp is the constant in terms of the partial pressures of the substances and K x is expressed in terms of the mole fraction.
Le Chatelier's principles, also known as the law of equilibrium, are used to predict the effects of some changes in a system in chemical equilibrium (such as changes in temperature or pressure). The principle is named after the French chemist Henry Louis Le Chatelier.
Le Chatelier said that equilibrium adjusts the forward and backward responses to accept changes that affect the equilibrium conditions.
Le Chatelier's principle can be used to predict the behavior of a system based on changes in pressure, temperature or concentration. Le Chatelier's principle implies that adding heat to a reaction favors the endothermic direction of a reaction as this reduces the amount of heat produced in the system.
Effect of Concentration Changes on Equilibrium and Product Formation
According to Le Chatelier's principles, the only balanced way to ingest more reagents is to increase product accumulation. The direct reaction is favored when the concentration of the reagent increases. The reaction equilibrium shifts towards the use of reagents in the reaction, which lowers the concentration of the reagents.
Similarly, adding product (concentration / pressure) increases the reaction backwards to decrease the concentration of the product. A reverse reaction is favored when the reagent concentration decreases and the reaction equilibrium shifts in the direction of reagent production and reagent concentration. Reagents will be more.
Effect of Change of Volume, Pressure, or Inert Gas on Equilibrium and Product Formation
Kp = Kc (RT)Δn = Kc (p/v)Δn
Change of volume, pressure, or inert gases has no effect on reactions of liquids and solids. They may have an effect in gaseous reactions and that too only when the difference in the sum of the number of reactant and product molecules (∆n) is not zero.
When ∆n = 0:
As per the Le Chatelier’s principles, there will be no effect on Equilibrium and Product Formation on changing the volume, pressure or inert gas.
When ∆n = +ve:
Increase of pressure or decrease in volume will decrease the formation of the product. Decrease of pressure or increase of volume shall have the opposite effect of increasing the product formation.
Effect of Change of Temperature on Equilibrium and Product Formation
The individual reaction in the equilibrium can be either endothermic or exothermic. Likewise, at equilibrium net energy involved may make the reversible reactions either endothermic or exothermic.
According to Le Chatelier’s Principles,
- In exothermic equilibrium, an increase in temperature decreases the product formation and decrease in temperature increases product formation.
- In endothermic reactions, an increase in temperature increases the product formation and decrease in temperature decreases the product formation.
Application of Le Chatelier’s
- The Le Châtelier principle can be used to stimulate the formation of a desired product in chemical reactions.In the Haber process for the industrial synthesis of ammonia, nitrogen gas and hydrogen gas react in the reaction N2 + 3H2 → 2NH3 to form ammonia gas; the process is exothermic, i.e. H. One that gives off heat.
- The principle of Le Chatelier can be applied as follows to understand the effect of pressure changes on systems in equilibrium. 1) When the partial pressure of one of the gaseous reactants or products is increased, the equilibrium position is shifted in order to decrease its partial pressure.
- Contact process in the production of sulfuric acid and synthesis of methanol.
- Le-Chatelier’s principle of equilibrium is used in the industrial applications in the scheme of reaction, that involves certain parameters like pressure, temperature, concentration of reaction and species with a single parameter that results in the change of equilibrium leading to undesired product formation.
Key takeaway
In a chemical equilibrium, the forward and reverse reactions occur at equal rates, and the concentrations of products and reactants remain constant, in broad terms, thermodynamics deals with the transfer of energy from one place to another and from one form to another. The key concept is that heat is a form of energy corresponding to a definite amount of mechanical work. The equilibrium established between the unionised molecules and the ions in the solution of weak electrolytes is called ionic equilibrium.
References:
1. Engel T. & Reid P., Physical Chemistry 3rd Ed. Pearson (2013).
2. McQuarrie, D. A. & Simon, J. D. Molecular Thermodynamics Viva Books Pvt. Ltd.: New Delhi (2004).
3. Kheterpal S.C., Pradeep’s Physical Chemistry, Vol. I & II, Pradeep Publications.