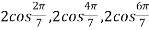Unit 1
Complex Numbers
1.1: Review: Basic of Complex Numbers
There is no real number x that satisfies the polynomial equation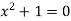 
. To permit the solution of this and similar equation, the set of complex number is introduced.
a) Complex Numbers: A complex number is an ordered pair of real numbers and is of the form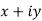 
, where x and y are real numbers and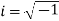 
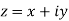
Also x is real part of z denoted by R(z) and y is the imaginary part of z denoted by I(z) .
b) Equal complex numbers: Two complex numbers are equal when there real and imaginary parts are equal i.e.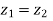
if and only if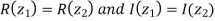 
i.e. (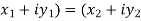
) if and only if 
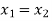and 
.
1) Addition: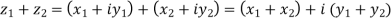 
i.e adding real and imaginary parts and result is again a complex number.
2) Subtraction: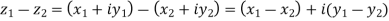 
i.e subtracting real and imaginary parts and the result is again a complex number.
3) Multiplication: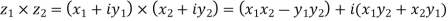 
4) Quotient: 
The sum, difference, product and the quotient of a complex numbers are itself a complex number.
Cartesian form of z: A complex number is an ordered pair of real numbers and is of the form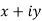 
, where x and y are real numbers and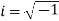 
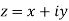
Also x is real part of z denoted by R(z) and y is the imaginary part of z denoted by I(z)
Polar form of a complex number: Every complex number z can be written in the form
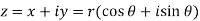
Where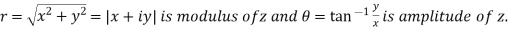 
Also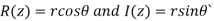 
Exponential form of z: The exponential form of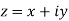 
is given by
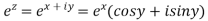
Modulus of complex number: The number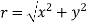 
is called the modulus of
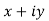denoted by
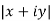or |z| or mod z .
Ex:
Argument of complex number: The angle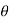 
is called the amplitude or argument of
.
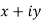The amplitude 
has infinite number of values. For any non zero complex number z, there is only one and one value of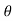
in 
The value of 
which lies between 
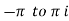s called the principle value of the amplitude.
c) Conjugate numbers: A pair of complex numbers
and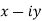 
are said to be conjugate to each other denoted by z and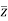 
If two complex numbers are equal then so its conjugate.
Important points: If conjugate of z is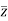
n then
1)
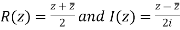
2)
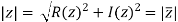
3)
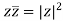
4) 
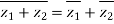
5)
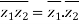
6)
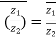where
7) 
8) 
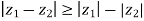
Dot and Cross Product
Let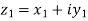 
and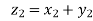 
be two complex numbers.
The dot product of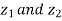 
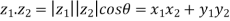
The cross product of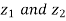 
is given by
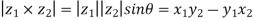
Example1: Express in the form of a + ib :
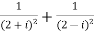
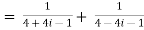
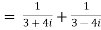
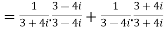
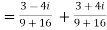
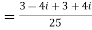
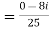
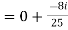
Example2: find the modulus of 
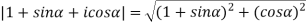
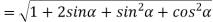
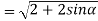
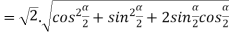
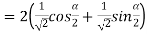
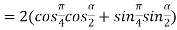
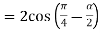
Example3: If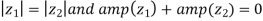 
then show that 
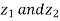are conjugate complex numbers?
Let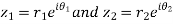 
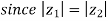
Also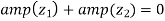 
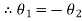
Again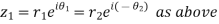 
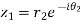
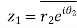
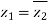
Hence both of them are conjugate to each other.
Example4: If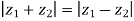 
, then show that the difference of the amplitude of
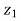and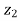
Is
Let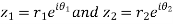 
| 
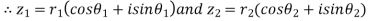
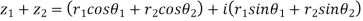
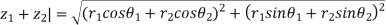
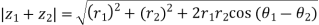
Similarly
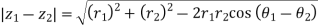
So,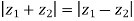 
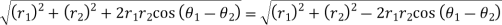
So,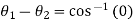 
Therefore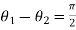 
Try: If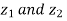 
be two complex numbers. Show that
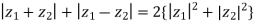
Example5: If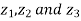 
be the vertices of an isosceles triangle, right angled at 
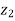, prove that
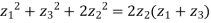
The triangle ABC is isosceles A
BC when rotated with 90 degree coincide
With BA.
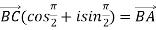
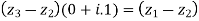
Squaring on both sides
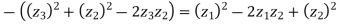
So,
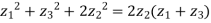
Equation of a circle in the complex plane:
The equation of the circle in the complex plane is given by
Where the center of the circle is point “a” and radius of circle is “r”.
If n be
(i) A positive or negative integer then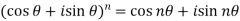 
(ii) A positive or negative fraction then one of the value of
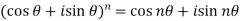
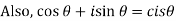
Note:
1) 
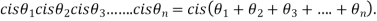
2)
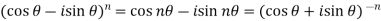
3) 
Some example based on above theorem:
- Find the value of
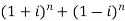
Sol: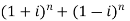 
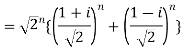
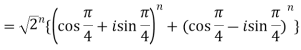
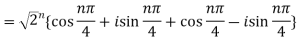
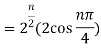
2. Find the value of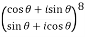 
Sol: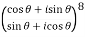 
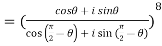
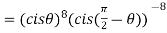
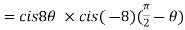
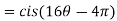
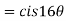
3. If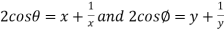 
Then find out the values of : a)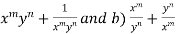
Sol: Let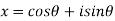 
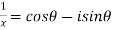
By Demoviers theorem
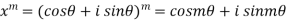
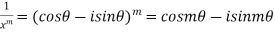
Similarly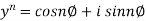 
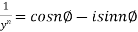
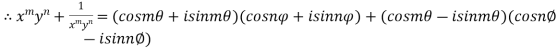
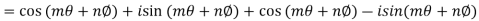
Second part is left for exercise.
4. If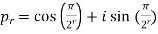 
,then find out the limiting value of the product series
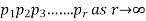
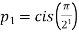
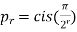
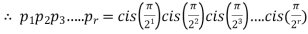
Sol: Given can be written 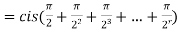as
……………….
as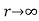
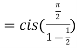by geometric progression
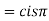
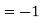
5. If p=cisx and q =cisy then show that
a)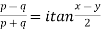 
b)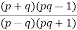 
a)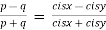 
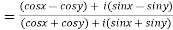
After rationalizing we get
=
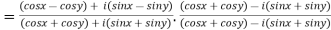
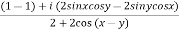
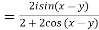
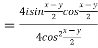
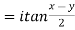
Second part is for exercise.
6. If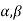 
are the roots of the equation 
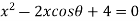.prove that
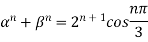
Sol: If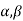 
are the roots of the equation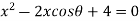 
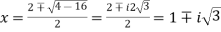
Therefore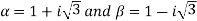 
So,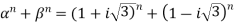 
}
= 
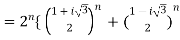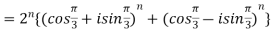
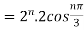
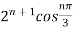
1.5 Expansion of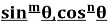 
in terms of sine and cosines of multiple of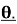 
If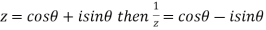 
By De Moivre’s Theorem
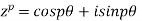
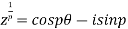
Therefore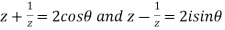 
Also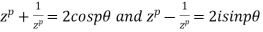 
This method is used to to expand the power of 
or their products in a series of sine and cosines o
f multiples of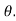
BINOMIAL THEOREM
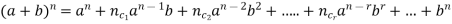
Use: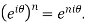 
Example 1: Prove that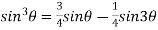 
-
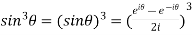
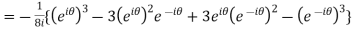
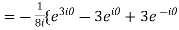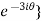
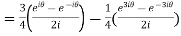
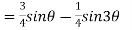
Example 2: If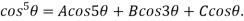 
then find out the values of A ,B and C
Given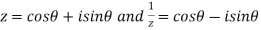 
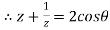
So,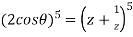 
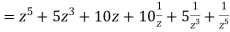
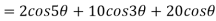
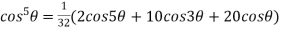
Therefore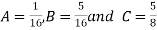 
Example 3:Expand the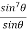 
in power of sine
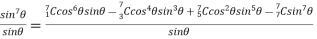
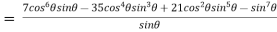
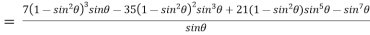
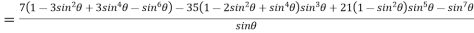
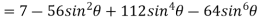
1.6 Expansion of sin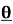n
,cosn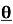
in terms of sin
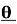and cos
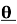respectively:
If n is a positive integer
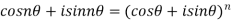
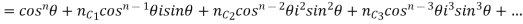
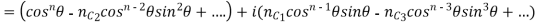
Equating real and imaginary parts from both sides ,we get
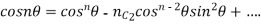
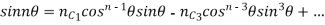
Also
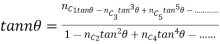
Example 1: Prove that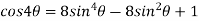 
Sol: Using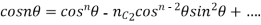 
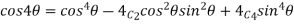
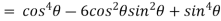
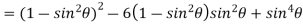
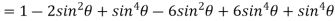
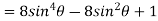
Example 2: If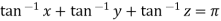 
then show that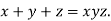 
Sol: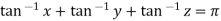 
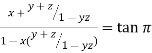
On solving
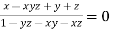.We get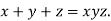 
Example 3: If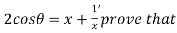 
(i)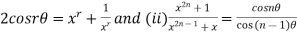 
As given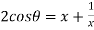 
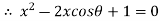
So,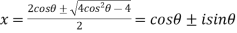 
Taking positive sign of x we get
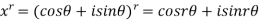
Adding above two equations
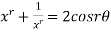
Similarly the same result is obtained for negative values of x
(ii) 
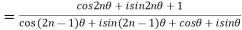
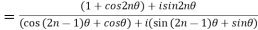
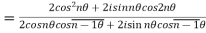
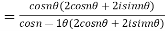
A number w is called the nth root of a complex number z if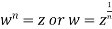 
.
From De Moivre’s theorem, if n is an integer,
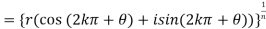
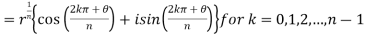
Which give us nth different roots of z, provided 
If n is a rational number such that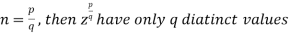 
Where n=0,1,2,…..,q-1.
EULER’S FORMULA:
It provide us the relation between exponential and trigonometric functions
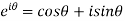
Which is called Euler’s formula.
It can be also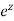 
=
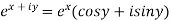
Example 1: If z is fifth root of unity i.e. 
then find all the values of z?
Sol: Given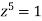 
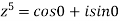
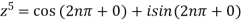
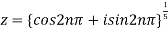
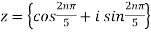
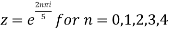
Therefore roots of z are 1,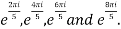
Try: find the square root of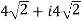 
Example 2: Find out the roots of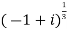 
?
Sol: 
The roots of given numbers are:
For n=0,
For n=1,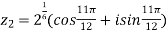
Foe n=3,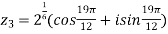
Example 3: Find the equation whose roots are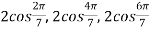 
Let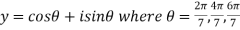 
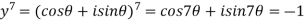
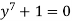
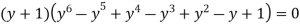
We will leave (y+1)=0 which corresponds to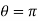 
Then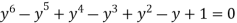 
Diving each term by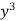 
and rearranging
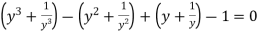
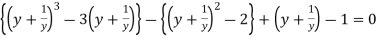
Let y + 
= x = 2cos
then above can be written as
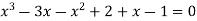
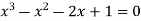
Which is the required equation.
Example 4: If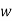 
is a complex cube root of unity then prove that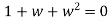 
Since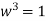 
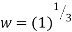
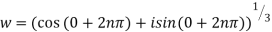
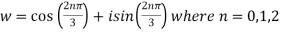
Therefore roots of w are
For n=0, we get w=1
For n=1,we get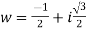 
For n=2, we get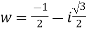 
Again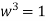 
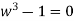
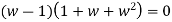
But w - 1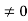
Therefore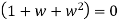 
Example 5: form the equation whose roots are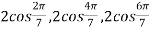 
Let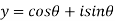 
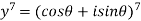
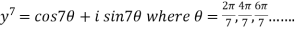
Therefore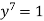 
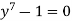
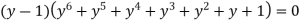
When ( y - 1 )=0 this gives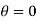 
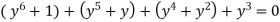by re arranging
Dividing each term by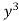 
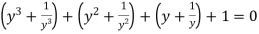
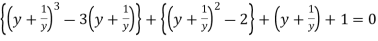
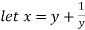
Therefore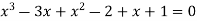 
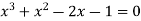……. (i)
Since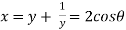 
Also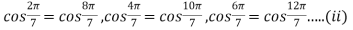 
Hence roots of the equation (i) are
