Unit 3
Valuation of Annuities
An annuity is a financial commodity that pays out fixed amounts of money at regular intervals. Financial firms, usually life insurance companies, produce annuities to provide a customer with a daily income.
Since it provides a person with guaranteed income, an annuity is a good alternative to some other investments as a source of income. Annuities, on the other hand, are less liquid than stock transactions since the initial lump sum deposit cannot be withdrawn without penalty. A person pays a lump sum to the annuity issuer when the annuity is issued (financial institution). The issuer then keeps the money for a set period of time (called an accumulation period). Following the accumulation period, the issuer is required to make predetermined payments to the person at predetermined intervals.
Individuals who want a predictable retirement income typically purchase annuities.
3.1.1 Types of Annuities:
Annuities are divided into several categories based on the frequency and form of payments they make. Annuities, for example, may have their cash flows charged at various times. Payments can be made once a week, twice a week, or once a month. The following are the most common forms of annuities:
Fixed annuities
Fixed-payment annuities are a form of annuity. Although the payments are assured, the rate of return is typically low.
Variable annuities
Annuities that allow a person to choose from a variety of investments and receive a monthly income based on the performance of those investments. Variable annuities do not guarantee a certain amount of money, but they provide a higher rate of return than fixed annuities.
Life annuities
Life annuities guarantee a set amount of money to their owners before they die.
Perpetuity
An annuity that pays out cash flows indefinitely with no end date. Financial instruments that provide the holder with everlasting cash flows are exceedingly rare.
Consol, a UK government bond, is the most well-known example. Consols were first published in the mid-eighteenth century. The bonds had no set end date and could be redeemed at the discretion of the Parliament. The UK government, on the other hand, redeemed all consols in 2015.
3.1.2 Valution of annuities:
The present value of annuities is determined by discounting potential cash flows and calculating the present value of the cash flows. The following is a general method for calculating the value of an annuity:
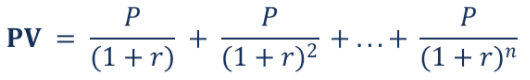
Where:
● PV = Present value of the annuity
● P = Fixed payment
● r = Interest rate
● n = Total number of periods of annuity payments
Perpetuity valuation differs from other valuations in that it does not have a set end date. As a result, the value of the perpetuity is calculated using the formula:
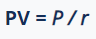
3.2.1 Calculating the Present Value of an Ordinary Annuity:
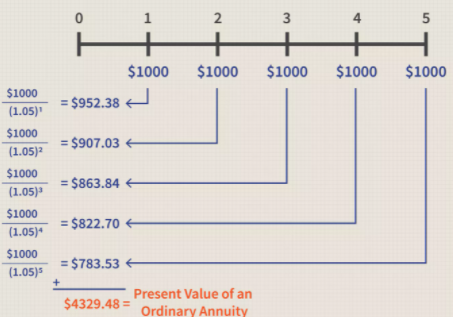
A present value (PV) calculation, in comparison to a future value calculation, informs you how much money you'll need now to make a series of payments in the future, assuming the same interest rate.
Here's how a present value estimate will look using the same example of five $1,000 payments made over a five-year period. It indicates that $4,329.58 will be enough to make those five $1,000 payments if invested at 5% interest.
This is the applicable formula:
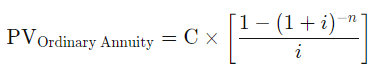
If we plug the same numbers as above into the equation, here is the result:

3.2.2 Calculating the Present Value of an Annuity Due:
Similarly, the formula for determining the present value of an annuity due accounts for the fact that payments are made at the start of each term rather than at the end.
This formula, for example, may be used to determine the present value of your future rent payments as defined in your contract. Let's say your rent is $1,000 a month. We can see how much the next five months will cost you in terms of present value if you kept your money in a 5 percent interest account.
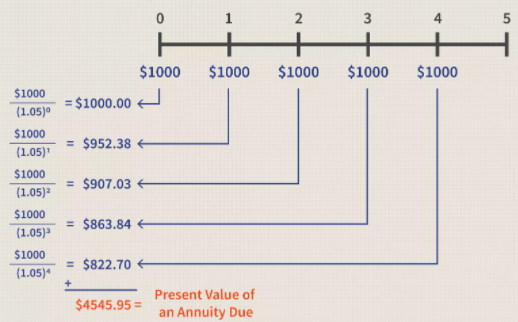
This is the formula for calculating the present value of an annuity due:
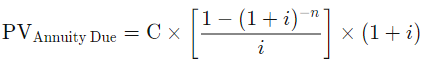
So, in this example:
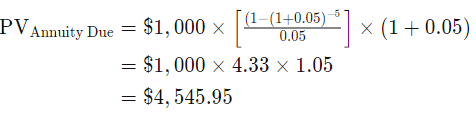
The deferred annuity formula is used to calculate the present value of a deferred annuity that is promised to be paid after a certain period of time. It is calculated by estimating the present value of a future payout by taking the rate of interest and time into account.
The word "deferred annuity" applies to a postponed annuity in the form of instalment or lump-sum payments rather than an immediate stream of profits. It's simply the current value of an annuity payout in the future. Ordinary annuity payment, effective rate of interest, number of payment terms, and deferred periods are all included in the formula for a deferred annuity based on an ordinary annuity (where the annuity payment is made at the end of each period).
The following is a representation of a Deferred Annuity based on an ordinary annuity:

where,
● P Ordinary = Ordinary annuity payment
● r = Effective rate of interest
● n = No. of periods
● t = Deferred periods
Annuity payment due, effective rate of interest, amount of payment intervals, and deferred periods are all included in the formula for a deferred annuity based on annuity due (where the annuity payment is made at the start of each period).
The following is a representation of a Deferred Annuity dependent on annuity due:
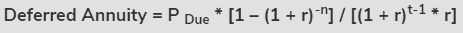
● P Due = Annuity payment due
● r = Effective rate of interest
● n = No. of periods
● t = Deferred periods
● Deferred Annuity Calculation (Step by Step)
The following steps can be used to calculate the formula for a deferred annuity using an ordinary annuity:
● Step 1: To begin, figure out how much the annuity payment will be and whether it will be made at the end of each period. The symbol for it is P Ordinary.
● Step 2: Next, divide the annualised rate of interest by the amount of periodic payments in a year to get the effective rate of interest, which is denoted by r. r = Annualized rate of interest / No. periodic payments in a year
● Step 3: Next, find the total number of periods, which is the product of the number of years and the number of periodic payments in a year, and is denoted by n. n = Number of years * Number of periodic payments in a year
Step 4: Next, calculate the payment deferment duration, which is denoted by t.
Step 5: Finally, as shown below, the deferred annuity can be calculated using ordinary annuity payments (step 1), an acceptable rate of interest rate (step 2), a number of payment intervals (step 3), and deferred periods (step 4).
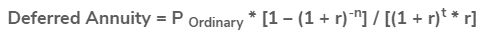
The following measures can be used to calculate the formula for a deferred annuity using annuity due:
● Step 1: Determine the amount of the annuity payment and whether it will be made at the beginning of each year. P Due is the symbol for it.
● Step 2: Next, divide the annualised rate of interest by the amount of periodic payments in a year to get the effective rate of interest, which is denoted by r. r = Annualized rate of interest / No. periodic payments in a year
● Step 3: Next, measure the total number of cycles, which is the product of the number of years and the number of periodic payments in a year, and is denoted by n.
● Step 4: Next, calculate the payment deferment duration, which is denoted by t.
● Step 5: Finally, the deferred annuity can be calculated using the following steps: annuity payment due (step 1), effective rate of interest rate (step 2), number of payment periods (step 3), and deferred periods (step 4).
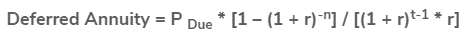
Examples:
Consider the case of John, who received a deal to lend $60,000 today in exchange for twenty-five annual payments of $6,000 each. The annuity will begin five years from now, with a 6-percent effective rate of interest. If the payout is an ordinary annuity with annuity due, determine if the agreement is feasible for John.
● Given, P Ordinary = $6,000,000
● r = 6%
● n = 25 years
● t = 5 years
Deferred Annuity Calculation If the payment is Ordinary Due, the deferred annuity can be computed as follows:
Annunity postponed

Deferred Annuity = $57,314.80 ~ $57,315
Deferred Annuity will be –
John does not lend the money in this situation since the deferred annuity is worth less than $60,000.
Calculation of Deferred Annuity if payment is Annuity Due
● Given, P Due = $6,000,000
● r = 6%
● n = 25 years
● t = 5 years
As a result, the deferred annuity can be determined using the formula:
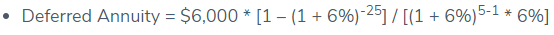
Deferred Annuity = $60,753.69 ~ $60,754
John can lend the money in this situation because the deferred annuity is worth more than $60,000.
● The present value of an m-monthly payable annuity is calculated as follows: PV = (annual payment)· 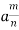 = (annual payment)·
= (annual payment)· 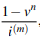 , where n denotes the number of years and v denotes the average effective interest rate.
, where n denotes the number of years and v denotes the average effective interest rate.
● A continuous annuity's present value is calculated as follows: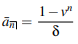
● A continuous annuity's accumulated value is:
● A continuous varying annuity's present value is:
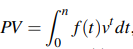 , assuming a constant effective rate of interest I per time and payment at the precise moment t as determined by f(t)dt?
, assuming a constant effective rate of interest I per time and payment at the precise moment t as determined by f(t)dt?
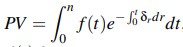 , f(t)dt assumes a varying rate of interest t and payment at the exact moment t
, f(t)dt assumes a varying rate of interest t and payment at the exact moment t
● Immediate increasing (or decreasing) in arithmetic progression of the present value of an annuity:
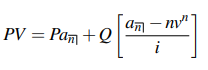
where P is the initial payment sum and Q is the amount that increases with each subsequent payment (Note: Q may be negative.)
This is referred to as an increasing annuity if P = 1 and Q = 1.
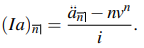
When P = n and Q = 1, the annuity is said to be decreasing, and

● In arithmetic progression, the present value of a perpetuity-immediate increases:
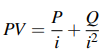
where P is the first payment's sum and Q > 0 is the amount that each subsequent payment grows by.
● Present value of an immediate annuity in which the first payment is 1 and subsequent payments increase (or decrease) geometrically with the typical ratio 1+k:

● The present value of an immediate perpetuity in which the first payment is 1 and subsequent payments increase (or decrease) in geometric progression with the common ratio 1+k, where k I
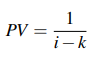 .
.
Understanding annuities is essential for understanding loans and investments that require or produce regular payments. For example, how much of a mortgage can I afford if my monthly income is only $1,000? How much money will I have in my IRA account after depositing $2,000 at the start of each year for 30 years at a 5% annual interest rate, compounded daily?
An annuity is a collection of payments made for a set period of time. The time period is usually one year, which is why it is called an annuity, but it can be shorter or longer. The periodic rent is the term for these regular payments. The sum of all contributions is the value of the annuity.
Payments on an annuity due are made at the start of each time period, while payments on an ordinary annuity are made at the end of the time period. Ordinary annuities make up the majority of annuities.
The future value of an annuity is the value of evenly spaced payments at some point in the future, similar to the future value and present value of a dollar, which is the future value and present value of a lump-sum payment. The present value of an annuity is the present value of potential payments that are evenly spaced.
3.5.1 A future value of annuity:
An annuity's future value is essentially the amount of each payment's future value. The number of the geometric series is the equation for the future value of an annuity due:
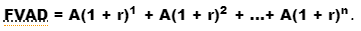
The number of the geometric series is the equation for the future value of an ordinary annuity:
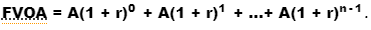
Without going into detail, just remember that the future value of an annuity is the number of the geometric sequences shown above, and that these quantities can be simplified using the formulas below: where A denotes the annuity payment or periodic rent, r denotes the interest rate per year, and n denotes the number of periods.
The future value of an ordinary annuity (FVOA) is calculated as follows:

And the future value of an annuity due (FVAD) is:
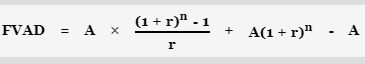
Note that the difference between FVAD and FVOA is:
FVAD = 0 + A(1 + r)1 + A(1 + r)2 + ...+ A(1 + r)n-1+ A(1 + r)n.
FVOA = A(1 + r)0 + A(1 + r)1 + A(1 + r)2 +... + A(1 + r)n-1 + 0.

To put it another way, the difference is simply the interest received during the previous compounding era. The last payment of an ordinary annuity receives no interest since it is made at the end of the term, while the last payment of an annuity due earns interest during the last compounding period.
3.5.2 The present value of annuity:
The sum of the present values of each annuity payout is the present value of an annuity (PVA). The present value of an annuity is the amount of the present values of each of those instalments, since the present value of a lump sum payment is essentially the future value of that payment divided by the interest factor (1 + r)n:
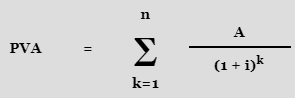
The sum of this geometric progression can be simplified to:

3.5.3 Calculating the Interest rate:
We conclude our discussion of annuities by noting that r in the formula for the present value of annuities cannot be solved algebraically, so we can only estimate r even though we know the annuity payment, the number of time intervals, and the present value. It's possible to measure r by guessing values, looking it up in special tables that map r against the annuity payment A, or using a graphing calculator to graph the annuity payment's value as a function of interest for a given present value. The interest rate is where the line representing the rate of interest intersects the line representing the annuity payment in the above case.
References