Unit 2
Present Value Calculation and Discount rate
Interest is charged or withheld up front in certain financial transactions. Selling a financial security for less than its face value is a popular way to raise funds for a short-term loan. The face value of the loan is repaid when the loan matures. A Treasury Bill, for example, is a discount instrument; the discount is the difference between the selling price and the face value of a discount security.
The nominal principal (face value) must be changed to account for the interest withdrawn, which affects the rate of interest rather than the quoted rate of discount.
The effective principal of the loan after interest is deducted is Effective principal = Nominal principal (1 Rate of Discount) if the loan term is one year.
● The nominal principal is A and the effective principal is A(0) (1).
● If the quoted discount rate is d, we have
 …….1.16
…….1.16
And

● Over the lifetime of the discount instrument, the equivalent effective rate of interest I is
 ..1.17
..1.17
from which we have
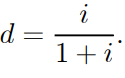
Combining (1.4) and (1.17), we can see that
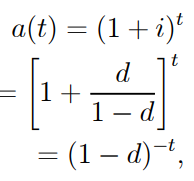
which is the accumulated value of 1 at time t at the rate of discount d.
● When the loan term is less than one year, we can first measure the rate of interest over the loan period, and then use the compounding principle to calculate the effective rate of interest.
● Assuming the loan term is 1/m year, the nominal rate of discount is denoted by d. (m).
● A(1/m) is the nominal principal, and the interest deducted is
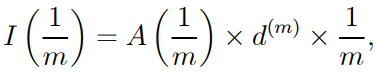
so that the effective principal is

and the rate of interest charged over the (1/m)-year period as

● Hence, the annualized equivalent nominal rate of interest is
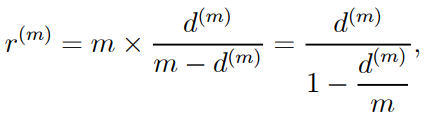 …1.18
…1.18
and the annual effective rate of interest is
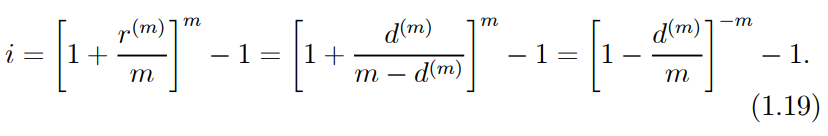
For a discount instrument with a maturity of 1/m year (m > 1), we compute the accumulation function a(t).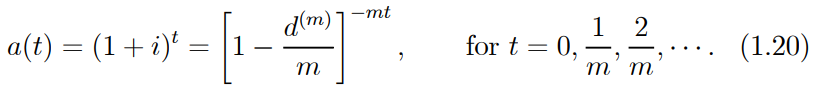 ….1.20
….1.20
● From (1.19) we have
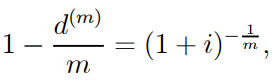 …..1.12
…..1.12
● so that from (1.18) we conclude
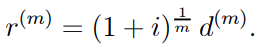 ….1.22
….1.22
Example 1.11:
A 3-month Treasury Bill has a discount rate of 6% per year. What is the effective annual rate of interest? What is the worth of 1 in 2 years accumulated?
Solution:
The interest rate for the three-month cycle is
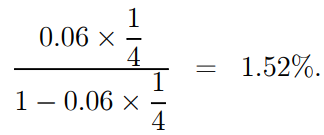
As a result, the quarterly equivalent nominal rate of interest is

and the effective annual rate of interest is
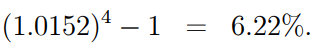
Using the cumulative value of 1 in 2 years (1.20),
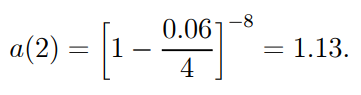
It's worth noting that this can be measured in a variety of ways.
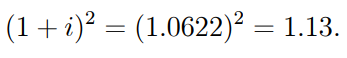
2.1.2 Present and future value:
● A 1-unit investment today will grow to (1 + I ) units by the end of the year if the effective rate of interest is i.
● The total number (1 + I ) is also known as the 1's potential value at the end of the year. In the same way, 1's potential worth at the end of year t is (1 + I ) t.
● A payment of (1 /(1 + I units made today would equal 1 unit at the end of the year.
● As a result, the present value of 1 to be charged at the end of year 1 is 1 /(1 + I ).
● 1 /(1 + I ) t is the present value of 1 to be charged at the end of year t.
Example 1.15: Calculate the present value of 1 to be charged at (a) the end of year 1, (b) the end of year 5, and (c) the end of year 6.5, provided I = 6%.
Solution: (a) The present value of 1 payable at the end of the first year is
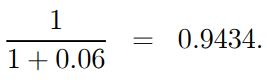
(b) and (c) are the correct responses, respectively.
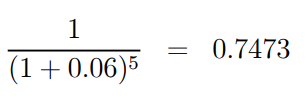
And
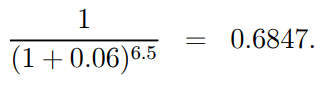
Example 1.16: Five years later, an insurance company proposes a policy that pays a lump sum of $50,000. How much would you pay for the plan if the interest rate was 8%?
Solution: The current value of the lump sum, which is equal to, is the reasonable amount to pay for this scheme.
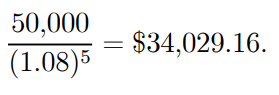
Example 1.17: A individual wishes to save $100,000 over the next eight years in order to fund his son's education. What percentage would he invest today if an investment portfolio offers him 8% compounded monthly?
Solution: We start by calculating the effective interest rate, which is equal to
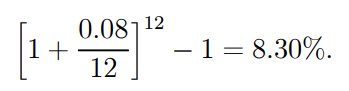
As a result, the current amount needed is
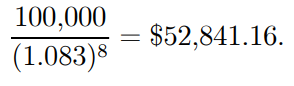
We now denote
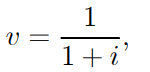 ……….1.30
……….1.30
which is the current value of 1 that will be charged a year from now.
● It's also known as the discount factor, and it's calculated by multiplying (1.17) and (1.30).
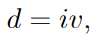 ………..1.31
………..1.31
● As a result, the current value of I is d.
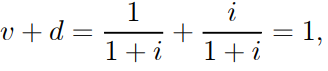 ………..1.32
………..1.32
that states that a unit payment's present value plus discount at time 1 equals the amount of its present value and discount.
● (1.30) means that a(1) = 1 + i.
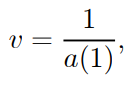
and we denote v ( t ) as the present value of 1 to be charged at time t for a general time t.
● Then
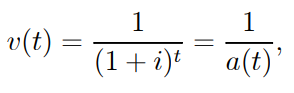 …………1.33
…………1.33
Which of the following is the discount factor for payments made at time t?
● The discount factor for payments at time t for a general accumulation function a ()
is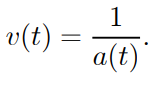
Example 1.18: If (a) interest is compounded semiannually at the nominal rate of 8% per year and (b) the simple-interest approach is used at 8% per year, find the balance of the present values of two $100 payments due at the end of years 4 and 9.
Solution: We begin by determining the discount factors v(4) and v(5) (9). The effective rate of interest in case (a) is
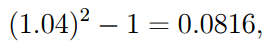
so that
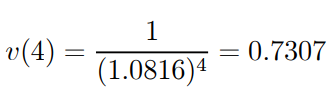
And
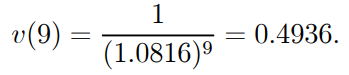
As a result, the two payments' present value is

For example, in case (b), we have
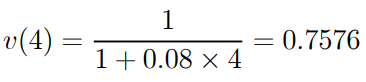
And
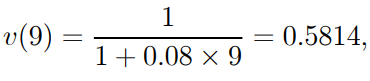
as a result of which the present value of the two payments equals

● We are now considering a payment of 1 at a later date. What will this payment be worth in the future at time t >?
● The response to this question is determined by how a potential payment accumulates with interest.
● Assume that any potential payment accrues interest according to the same accumulation function as a payment made at time 0.•
● Since a 1-unit payment gains interest over a period of t until time t, its accrued value at time t is ( t ).
● What is the potential value of this amount at time t if we assume a particular situation in which the 1-unit amount at time t has been accrued from time 0 and is not a new investment?
● To answer this question, we must first calculate the sum invested at time 0, which is equal to the present value of 1 due at time, i.e., 1/a( ). The investment's future value at time t is then given by

● We can see that the potential values of the two investments, i.e., a 1-unit investment at time versus a 1-unit sum accrued from time 0, are not always the same.
● They are, however, equal if
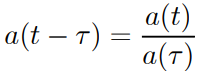 …………1.35
…………1.35
for t > τ > 0.
● The condition is satisfied by compound interest accumulation (1.35).
● If the principal is invested at the time or accrued from the past, the principal at time accumulates interest at the rate of I per year. We have, in particular,
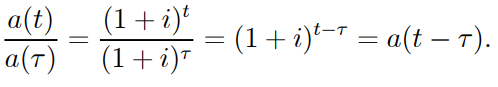
● Simple-interest accumulation, on the other hand, does not meet the condition (1.35). A unit payment's potential value at time t is equal to
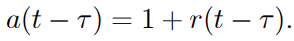
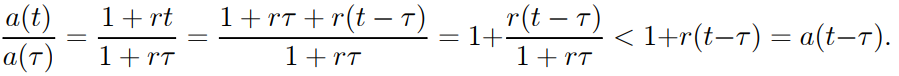
Example 1.19: Let a(t)=0.02t2 + 1 be the value. Calculate the potential value of an investment made at t = 5 with a one-time payment of one dollar and a two-time payment of two dollars at t = three.
Solution: At time 5, the future value is
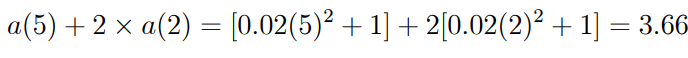
Example 1.20: Let (t) be equal to 0.01t. Calculate the potential value of an investment with a 1 payment now and a 2 payment at t = 5 with a 1 payment now and a 2 payment at t = 2.
Solution: The accumulation function is first derived from the force of interest, which is
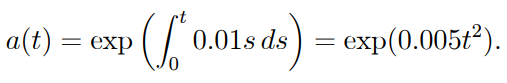
Thus, a(5) = exp(0.125) = 1.1331 and a(3) = exp(0.045) = 1.0460, yielding the investment's potential value as
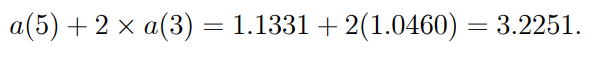
The effective interest rate is the interest rate that is multiplied only once over a given time span. For instance, a 12-percent annual effective interest rate means that interest is compounded only once a year at the end of the year.
The nominal interest rate, on the other hand, is the rate of interest multiplied more than once per time period. For example, a nominal interest convertible monthly (or compound monthly) rate of 12% means a monthly interest rate of 1%.
Effective and nominal discount rates, on the other hand, can be characterised as rates multiplied once per month and more than once per period, respectively.
Nominal interest rates are multiplied more than once every time span, as previously mentioned. i(p) denotes a nominal interest rate compounded p times per time period.
An effective rate of i(p)/p per any 1/p time period is referred to as a nominal rate of i(p).
If p.a. is used, it denotes a rate of 1% per half-year, or once a month. However, this cannot be expressed as a 12-percent-per-annum effective interest rate. This is due to the fact that if 1 percent is multiplied monthly, it would multiply to, resulting in an average interest rate of 12.68 percent.
Similarly, if I is the effective rate and i(p) is the nominal rate, the accumulation using I is 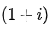 and using i(p), the accumulation will be
and using i(p), the accumulation will be 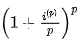 . This is due to the fact that an interest rate of i(p) /p is multiplied several times.
. This is due to the fact that an interest rate of i(p) /p is multiplied several times.
When we combine the two, we get

The relationship between an effective and nominal interest rate is given by this equation. Rearranging this provides us with
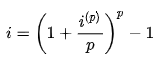
And
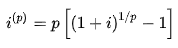
Nominal and effective discount rates can be described in the same way. dp denotes a nominal discount rate multiplied p times per time period. An efficient discount rate of dp/p per 1/p time span is equivalent to a nominal discount rate of dp.
The discount factor will be if d is the effective discount rate per time span.  per period of time The discount factor will be if dp is the nominal discount rate.
per period of time The discount factor will be if dp is the nominal discount rate. 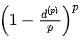 per period of time
per period of time
When we combine the two, we get
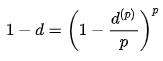
The relationship between an effective and nominal discount rate is given by this equation. As a result of rearranging this, we get:
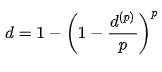
And
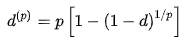
Example 1
A bank advertises an annual nominal interest rate of 8% compounded quarterly. Every year, an account holder wants to know what his effective interest rate is.
Here,
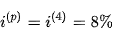

So, a nominal interest rate of 8% p.a. convertible quarterly translates to an average interest rate of 2% per quarter, or 8.243 percent per year.
Example 2
An investor puts money into a security that provides him with a p.a. successful return. He also puts an equivalent sum of money into a savings account that pays him almost the same amount of money at the end of a year, but at a monthly compounded interest rate. The investor is interested in learning more about the bank's nominal interest rate.
Here,
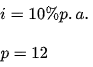
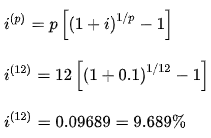
As a result, an effective interest rate of 10% is the same as a nominal interest rate of 9.689 percent compounded annually, or 9.689/12 percent = 0.8074 percent per month effective.
Discounting is the process of calculating present values from future values. The concepts of present and future values illustrate the idea of the time value of money, which states that in a world with positive interest rates, an amount of money has more value now than it would have in the future since we can spend it now and gain interest. We would only consider a future sum in comparison to a current sum if we are rewarded with a sufficient rate of interest. We may equate the value of a future sum to the value of a present sum by discounting future values. The discount rate, abbreviated as r, is the rate at which we discount a known future value in order to arrive at a present value. Equation (A.1) can be rearranged to give:
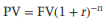
The n-year discount factor is defined as (1 + r)-n:
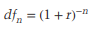
The n-year discount factor is denoted by dfn.
When the discount rate is 9%, the 3-year discount factor is:
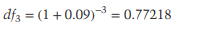
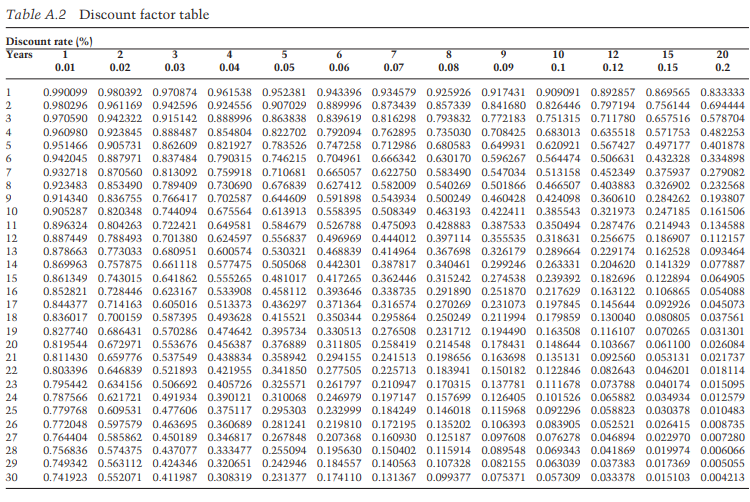
To get a discount function, we can measure discount factors for all possible interest rates and time periods. We don't have to measure discount factors because they've already been done for us. (Table A.2 contains discount tables for a variety of rates.)


We named the continuously compounded interest rate factor ern earlier. As a result, we can calculate the discount factor using a continuously compounded interest rate as follows:
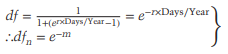 ……………A.11
……………A.11
In option pricing models, the continuously compounded discount factor is part of the formula. Discount factors can be calculated using the prices of government bonds. The conventional approach, as defined in most textbooks, requires one to first measure a discount factor from the price of a bond with only one remaining coupon, its last one. The discount factor is then used to measure the discount factors of bonds with ever-increasing maturities until the full discount function is obtained.
2.3.2 Present values with multiple discounting:
A single interest payment is often included in present values for short-term investments with a duration of less than one year. If there are multiple interest payments, any discounting must take this into consideration. If discounting occurs m times per year, we can derive the present value formula using equation (A.4):
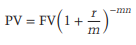 …………..A.12
…………..A.12
What is, for example, the present value of a total of £1,000 that will be paid in 5 years at a 5% discount rate and with semi-annual discounting?
We can see from equation (A.12) that:
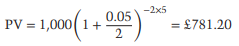
More frequent discounting has the effect of lowering the present value. Continuous discounting, like continuous compounding, is used to meet the limiting factor. The present value formula for continuous discounting can be derived using equation (A.6):
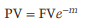 ……………….A.13
……………….A.13
If we use the same example as before, but this time with continuous discounting, we can measure the present value of £1,000 that will be obtained in 5 years as follows:
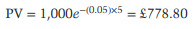
References