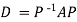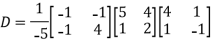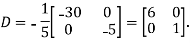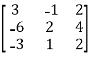UNIT 1
Matrices
Rank of a matrix-
Rank of a matrix by echelon form-
The rank of a matrix (r) can be defined as –
1. It has at least one non-zero minor of order r.
2. Every minor of A of order higher than r is zero.
Example: Find the rank of a matrix M by echelon form.
M = 
Sol. First we will convert the matrix M into echelon form,
M = 
Apply, 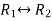 , we get
, we get
M = 
Apply 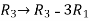 , we get
, we get
M = 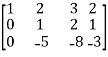
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form.
A = 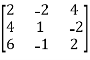
Sol. Convert the matrix A into echelon form,
A = 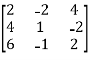
Apply 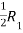
A = 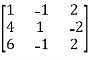
Apply 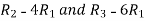 , we get
, we get
A = 
Apply 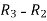 , we get
, we get
A = 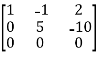
Apply 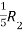 ,
,
A = 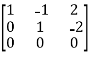
Apply 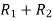 ,
,
A = 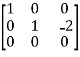
Therefore the rank of the matrix will be 2.
Example: Find the rank of a matrix A by echelon form.
A = 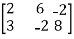
Sol. Transform the matrix A into echelon form, then find the rank,
We have,
A = 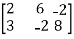
Apply, 
A = 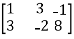
Apply  ,
,
A = 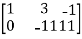
Apply 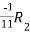
A = 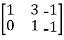
Apply 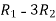
A = 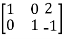
Hence the rank of the matrix will be 2.
Example: Find the rank of the following matrices by echelon form?
Let A = 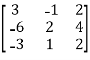
Applying 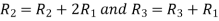
A 
Applying 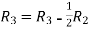
A 
Applying 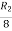
A 
Applying 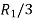
A 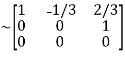
It is clear that minor of order 3 vanishes but minor of order 2 exists as 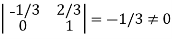
Hence rank of a given matrix A is 2 denoted by 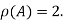
2. 
Let A = 
Applying 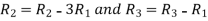

Applying 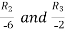
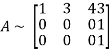
Applying 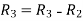
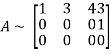
The minor of order 3 vanishes but minor of order 2 non zero as 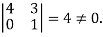
Hence the rank of matrix A is 2 denoted by 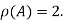
3. 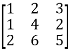
Let A = 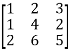
Apply 
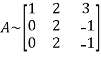
Apply 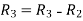

Apply 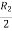

It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 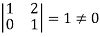
Hence the rank of given matrix is 2 i.e. 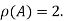
Rank of a matrix by normal form-
Any matrix ‘A’ which is non-zero can be reduced to a normal form of ‘A’ by using elementary transformations.
There are 4 types of normal forms –

The number r obtained is known as rank of matrix A.
Both row and column transformations may be used in order to find the rank of the matrix.
Note-Normal form is also known as canonical form
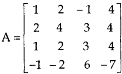
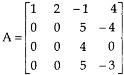
Example: reduce the matrix A to its normal form and find rank as well.
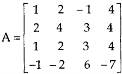
Sol. We have,
We will apply elementary row operation,
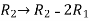
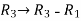
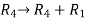
We get,
Now apply column transformation,
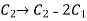
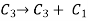
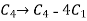
We get,

Apply
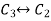 , we get,
, we get,

Apply  and
and 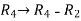

Apply 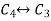

Apply 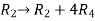 and
and 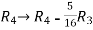

Apply 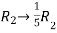 and
and 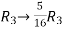

As we can see this is required normal form of matrix A.
Therefore the rank of matrix A is 3.
Example: Find the rank of a matrix A by reducing into its normal form.
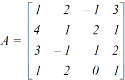
Sol. We are given,
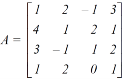
Apply



Apply
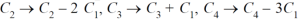
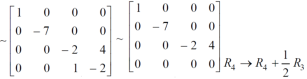
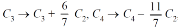

This is the normal form of matrix A.
So that the rank of matrix A = 3
System of linear equations
There are two types of linear equations-
1. Consistent 2. Inconsistent
Let’s understand about these two types of linear equations
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Where as,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-




This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) inconsistent equations-
If Rank of A ≠ Rank of C
Solving system of homogeneous and non-homogeneous equations-
Solution of homogeneous system of linear equations-
A system of linear equations of the form AX = O is said to be homogeneous , where A denotes the coefficients and of matrix and and O denotes the null vector.
Suppose the system of homogeneous linear equations is ,



It means ,
AX = O
Which can be written in the form of matrix as below,
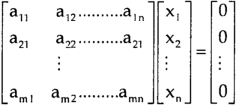
Note- A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n , then there will be an infinite number of solution.
Example: Find the solution of the following homogeneous system of linear equations,
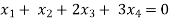

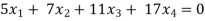
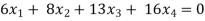
Sol. The given system of linear equations can be written in the form of matrix as follows,
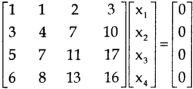
Apply the elementary row transformation,
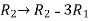
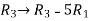
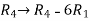 , we get,
, we get,
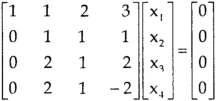
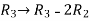
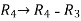 , we get
, we get
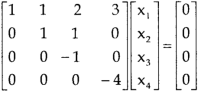
Here r(A) = 4, so that it has trivial solution,
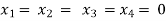
Example: Find out the value of ‘b’ in the system of homogenenous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) trivial solution
(2) non-trivial solution
Sol. (1)
For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
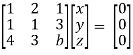
Apply 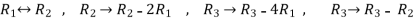 respectively , we get the following resultant matrices
respectively , we get the following resultant matrices
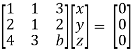
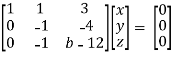
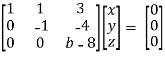
For non-trivial solutions , r(A) = 2 < n
b – 8 = 0
b = 8
Solution of non-homogeneous system of linear equations-
Example-1: check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
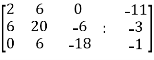
Apply 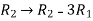 , we get
, we get
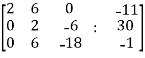
Apply 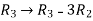
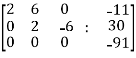
Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A,B]
That will be,
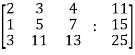
Apply 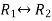
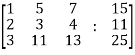
Now apply ,
We get,
 ~
~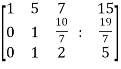 ~
~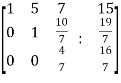
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,
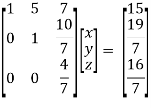
That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,
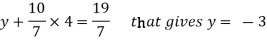
From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
First we will go through some important definitions before studying Eigen values and Eigen vectors.
1. Vector-
An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, …………xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn).
Where the numbers x1, x2, ………..,xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector.
If A be an mxn matrix then each row will be an n – vector & each column will be an m – vector.
2. Linear dependence-
A set of n – vectors. x1, x2, …….., xr is said to be linearly dependent if there exist scalars. k1, k2, …….,kr not all zero such that
k1 + x2k2 + …………….. + xrkr = 0 … (1)
3. Linear independence-
A set of r vectors x1, x2, ………….,xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that
x1 k1 + x2 k2 + …….. + xrkr = 0
Important notes-
- Equation (1) is known as a vector equation.
- If the vector equation has non – zero solution i.e. k1, k2, ….,kr not all zero. Then the vector x1, x2, ……….xr are said to be linearly dependent.
- If the vector equation has only trivial solution i.e.
k1 = k2 = …….=kr = 0. Then the vector x1, x2, ……,xr are said to linearly independent.
4. Linear combination-
A vector x can be written in the form.
x = x1 k1 + x2 k2 + ……….+xrkr
Where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
Results:
- A set of two or more vectors are said to be linearly dependent if at least one vector can be written as a linear combination of the other vectors.
- A set of two or more vector are said to be linearly independent then no vector can be expressed as linear combination of the other vectors.
Example 1
Are the vectors  ,
, 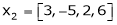 ,
, 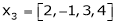 linearly dependent. If so, express x1 as a linear combination of the others.
linearly dependent. If so, express x1 as a linear combination of the others.
Solution:
Consider a vector equation,
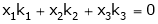
i.e. 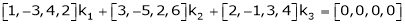
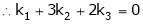
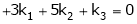
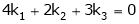
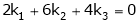
Which can be written in matrix form as,
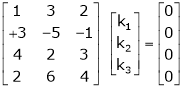
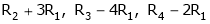
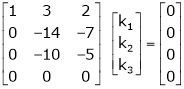
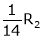
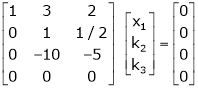

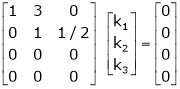
Here 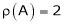 & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
& no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
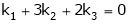
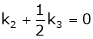
Put 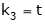
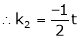 and
and
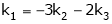
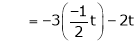
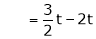
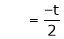
Thus 
i.e. 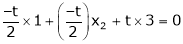
i.e. 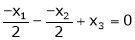
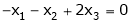

Since F11k2, k3 not all zero. Hence 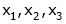 are linearly dependent.
are linearly dependent.
Example 2
Examine whether the following vectors are linearly independent or not.
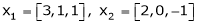 and
and 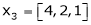 .
.
Solution:
Consider the vector equation,
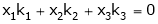
i.e. 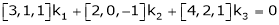 … (1)
… (1)
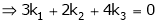
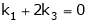
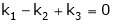
Which can be written in matrix form as,
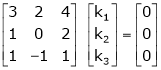
R12
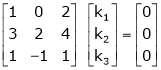
R2 – 3R1, R3 – R1
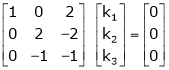
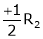
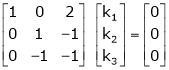
R3 + R2
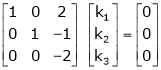
Here Rank of coefficient matrix is equal to the no. Of unknowns. i.e. r = n = 3.
Hence the system has unique trivial solution.
i.e. 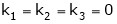
i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent.
Example 3
At what value of P the following vectors are linearly independent.
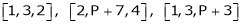
Solution:
Consider the vector equation.

i.e.
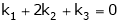
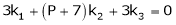
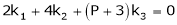
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of coefficient matrix is non zero.
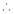 consider
consider 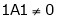 .
.
 .
.
i.e.
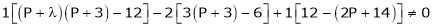
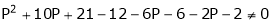

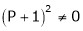
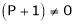
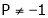
Thus for 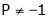 the system has only trivial solution and Hence the vectors are linearly independent.
the system has only trivial solution and Hence the vectors are linearly independent.
Note:-
If the rank of the coefficient matrix is r, it contains r linearly independent variables & the remaining vectors (if any) can be expressed as linear combination of these vectors.
Characteristic equation:-
Let A he a square matrix, 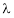 be any scalar then
be any scalar then 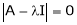 is called characteristic equation of a matrix A.
is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘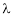 ’ be any scalar then,
’ be any scalar then,
1) 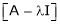 is called characteristic matrix
is called characteristic matrix
2) 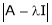 is called characteristic polynomial.
is called characteristic polynomial.
The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Eigen vector:-
Suppose 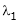 be an Eigen value of a matrix A. Then
be an Eigen value of a matrix A. Then 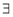 a non – zero vector x1 such that.
a non – zero vector x1 such that.
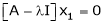 … (1)
… (1)
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value 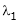 .
.
Properties of Eigen values:-
- Then sum of the Eigen values of a matrix A is equal to sum of the diagonal elements of a matrix A.
- The product of all Eigen values of a matrix A is equal to the value of the determinant.
- If
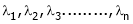 are n Eigen values of square matrix A then
are n Eigen values of square matrix A then  are m Eigen values of a matrix A-1.
are m Eigen values of a matrix A-1. - The Eigen values of a symmetric matrix are all real.
- If all Eigen values are non –zero then A-1 exist and conversely.
- The Eigen values of A and A’ are same.
Properties of Eigen vector:-
- Eigen vector corresponding to distinct Eigen values are linearly independent.
- If two are more Eigen values are identical then the corresponding Eigen vectors may or may not be linearly independent.
- The Eigen vectors corresponding to distinct Eigen values of a real symmetric matrix are orthogonal.
Example-1:
Determine the Eigen values of Eigen vector of the matrix.

Solution:
Consider the characteristic equation as, 
i.e. 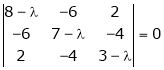
i.e. 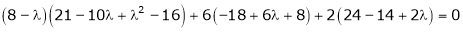
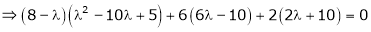
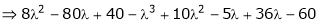
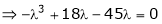
i.e. 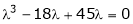
Which is the required characteristic equation.
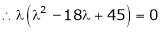
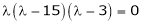
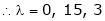 are the required Eigen values.
are the required Eigen values.
Now consider the equation
 … (1)
… (1)
Case I:
If 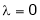 Equation (1) becomes
Equation (1) becomes
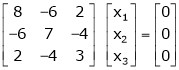
R1 + R2
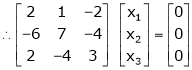
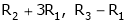
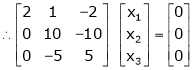
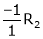
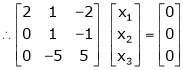
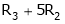
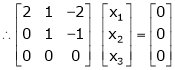
Thus 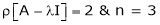
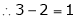 independent variable.
independent variable.
Now rewrite equation as,
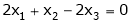

Put x3 = t
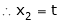 &
&

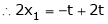
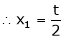
Thus 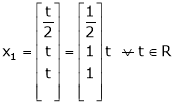 .
.
Is the eigen vector corresponding to 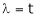 .
.
Case II:
If 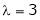 equation (1) becomes,
equation (1) becomes,

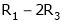
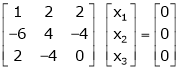
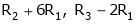
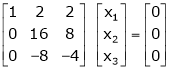
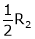
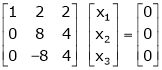
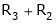
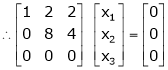
Here 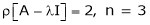
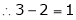 Independent variables
Independent variables
Now rewrite the equations as,
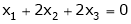
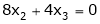
Put 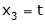
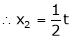 &
&
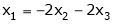
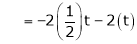

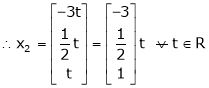 .
.
Is the eigen vector corresponding to 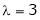 .
.
Case III:
If 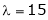 equation (1) becomes,
equation (1) becomes,
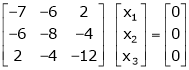

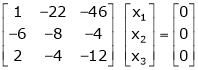
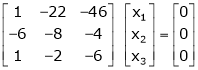

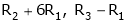
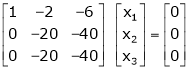
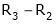

Here rank of 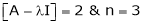
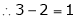 independent variable.
independent variable.
Now rewrite the equations as,
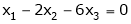
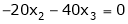
Put 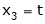

Thus 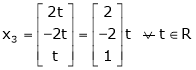 .
.
Is the eigen vector for  .
.
Example 2
Find the Eigen values of Eigen vector for the matrix.
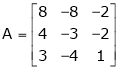
Solution:
Consider the characteristic equation as 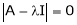
i.e. 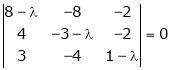
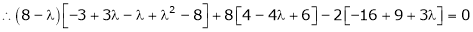
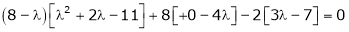
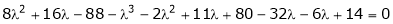
i.e. 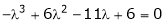
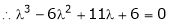
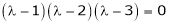
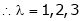 are the required eigen values.
are the required eigen values.
Now consider the equation
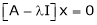 … (1)
… (1)
Case I:
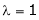 Equation (1) becomes,
Equation (1) becomes,
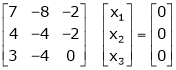
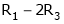
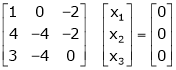

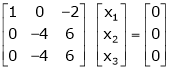
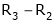
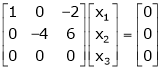
Thus 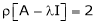 and n = 3
and n = 3
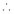 3 – 2 = 1 independent variables.
3 – 2 = 1 independent variables.
Now rewrite the equations as,
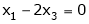
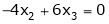
Put 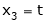
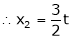 ,
, 
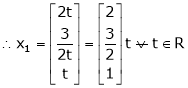
I.e.
The Eigen vector for 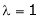
Case II:
If 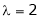 equation (1) becomes,
equation (1) becomes,
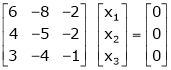

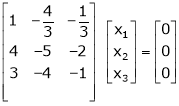
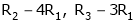
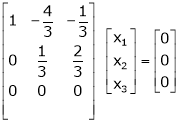
Thus 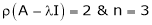
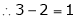
Independent variables.
Now rewrite the equations as,

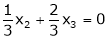
Put 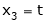
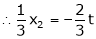
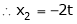
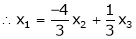
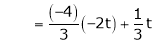
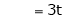
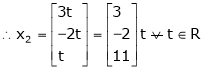
Is the Eigen vector for
Now
Case III:-
If 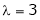 equation (1) gives,
equation (1) gives,
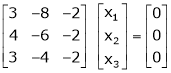
R1 – R2
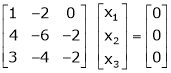
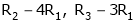
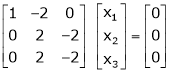
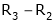
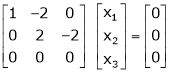
Thus 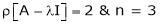
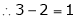
Independent variables
Now 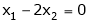
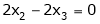
Put 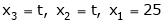
Thus
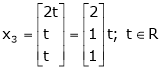
Is the Eigen vector for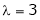
Statement-
Every square matrix satisfies its characteristic equation , that means for every square matrix of order n,
|A - 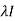 | =
| = 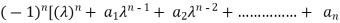
Then the matrix equation-
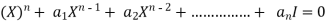
Is satisfied by X = A
That means
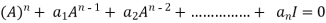
Example-1: Find the characteristic equation of the matrix A =  andVerify cayley-Hamlton theorem.
andVerify cayley-Hamlton theorem.
Sol. Characteristic equation of the matrix, we can be find as follows-
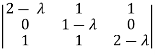
Which is,
( 2 -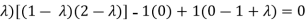 , which gives
, which gives
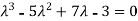
According to cayley-Hamilton theorem,
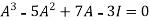 …………(1)
…………(1)
Now we will verify equation (1),
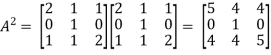
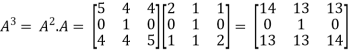
Put the required values in equation (1) , we get
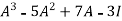
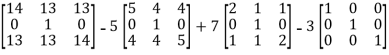
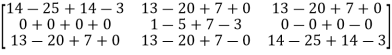
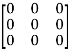
Hence the cayley-Hamilton theorem is verified.
Example-2: Find the characteristic equation of the the matrix A and verify Cayley-Hamilton theorem as well.
A = 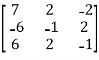
Sol. Characteristic equation will be-
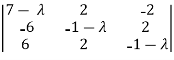 = 0
= 0
( 7 -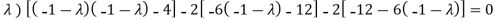
(7-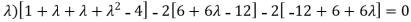
(7-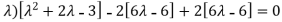
Which gives,
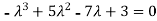
Or
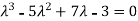
According to cayley-Hamilton theorem,
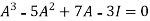 …………………….(1)
…………………….(1)
In order to verify cayley-Hamilton theorem , we will find the values of 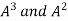
So that,
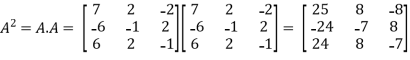
Now


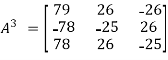
Put these values in equation(1), we get
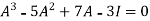
 = 0
= 0
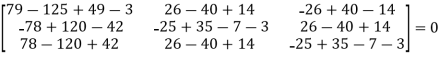

Hence the cayley-hamilton theorem is verified.
Example-3:Using Cayley-Hamilton theorem, find 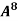 , if A =
, if A = 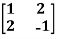 ?
?
Sol. Let A =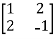
The characteristics equation of A is 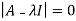
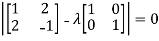
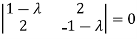
Or 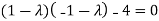
Or 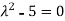
By Cayley-Hamilton theorem 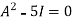
L.H.S. 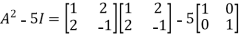
=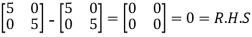
By Cayley-Hamilton theorem we have 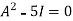
Multiply both side by 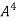
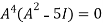 .
.
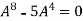
Or 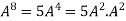
=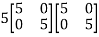
=
Quadratic forms & Nature of the Quadratic forms-
Quadratic form can be expressed as a product of matrices.
Q(x) = X’ AX,
Where,
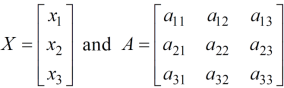
X’ is the transpose of X,
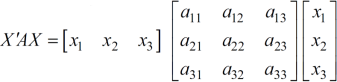
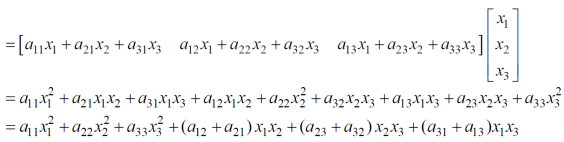
Which is the quadratic form.
Example: find out the quadratic form of following matrix.
A = 
Solution: Quadratic form is,
X’ AX

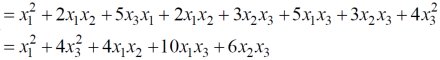
Which is the quadratic form of a matrix.
Example: find the real matrix of the following quadratic form:
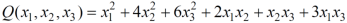
Sol. Here we will compare the coefficients with the standard quadratic equation,
We get,
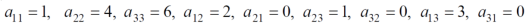
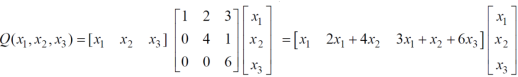
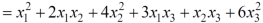
Diagonalization of matrices
Two square matrix 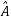 and A of same order n are said to be similar if and only if
and A of same order n are said to be similar if and only if
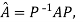 for some non singular matrix P.
for some non singular matrix P.
Such transformation of the matrix A into 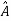 with the help of non singular matrix P is known as similarity transformation.
with the help of non singular matrix P is known as similarity transformation.
Similar matrices have the same Eigen values.
If X is an Eigen vector of matrix A then 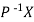 is Eigen vector of the matrix
is Eigen vector of the matrix 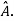
Reduction to Diagonal Form:
Let A be a square matrix of order n has n linearly independent Eigen vectors Which form the matrix P such that

Where P is called the modal matrix and D is known as spectral matrix.
Procedure: let A be a square matrix of order 3.
Let three Eigen vectors of A are 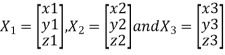 Corresponding to Eigen values
Corresponding to Eigen values 
Let 
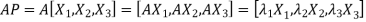 {by characteristics equation of A}
{by characteristics equation of A}
Or 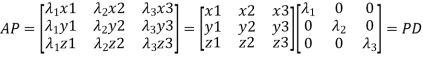
Or 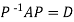
Note: The method of diagonalization is helpful in calculating power of a matrix.
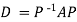 .Then for an integer n we have
.Then for an integer n we have 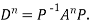
We are using the example of 1.6*
Example1: Diagonalise the matrix 
Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 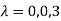 .
.
Then  and
and 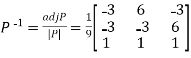
Also we know that 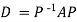
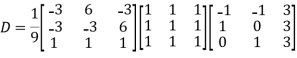

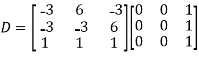
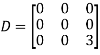
Example2: Diagonalise the matrix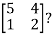
Let A =
The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values 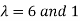 .
.
Then 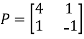 and also
and also 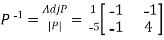
Also we know that