Unit-1
Introduction to Feedback Control System
Open loop systems:
This is the loop of control system without any feedback. In this the control action is not dependent on the desired output.
Fig. 1 open loop control system
Example of open Loop systems are the traffic signals, Automatic washing machine and in fields control d.c. Motor.
G(s) = c(s)/R(s) -------(1)
Closed loop systems:
This is a type of control system with feedback. In this type of system. The control action is dependent on the desired output.
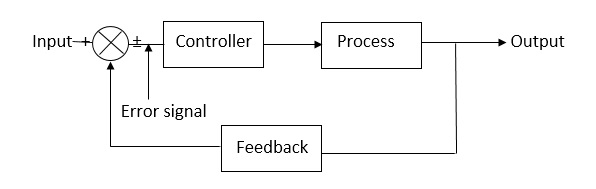Fig 2 Closed Loop control system
The error signal is again fed to controller to the error and get desired output.
G(s) – forward amplification
H(s) _ Reverse amplification
Above system is with negative feedback.
Positive feedback is used only in oscillators and other use is not known as discussing only negative feedback.
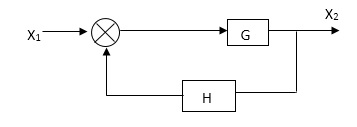
[ R(s) – c(s) H (S) ] G(s) = c(s)
R (s) G(s) = [1+G(s) H(s)] c(s)
C(s)/R(S) = G(S)/1+G(s) H(s)
S0, the transfer function of closed Loop system is
C(s)/ R(S) = G(s)/ 1+G(S) H(S) --------(2)
If numerator of above equation (2) is equalized to zero we get zeros of closed Loop Transfer function [G(S) = 0]
If dominator of equation (2) is equaled to zero we get polls of the closed loop transfer function [ 1+G(s) H(S) = 0]
1+ G(S) H(s) = 0 [ characteristic Equation]
Stability of the system is determined by the location of its poles.
Comparisons between open Loop and Closed Loop system
Open Loop System | Closed Loop system |
1.It does Not have any feedback. | 1. This system comprise of feedback |
2.As no feedback so easier to build. | 2.As it has feedback so difficult to build |
3.Theaccuracy of this system depends on the calibration of input. | 3.They are accuracy because of the feedback. |
4.Open Loop system are more stable. | 4.In closed Loop system stability depends on system components. |
5.optimization is not possible | 5. Optimization is possible |
6.These systems are not reliable. | They are more reliable |
Feedforward System:
The feedback system is which work to reduce the error it’s the system. In some system where the disturbances input can be provided beforehand, its effect can be eliminated by feedforward system.
Tracking System:
The main objective of such system is to trace any particular location as direction of a targeted value on continuous basic. The basic examples of tracking, Range tracking, Tracking in phased array radars.
Regulator System: The main objective of such systems is to maintain a designated characteristic they try to maintain a range of values is a machine for ex. Voltage regulator etc.
Key takeaway:
1) The open loop systems are without feedback.
2) The closed loop systems use feedback. In closed Loop system stability depends on system components
1.2.1 Electrical Networks
Q1) For the electrical network below find the equation for current i?
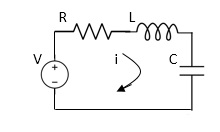
Sol: Applying Kirchoff’s voltage Law
V= Ri +Ldi/dt +1/c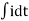
V= Rdq/dt + L d2q/dt2+q/c
Now By kirchoff’s current low
I= V/R+ 1/L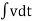 
+ cdv/dt
But V= dø/dt
I= 1/R dø/dt + 1/L ø+cd2ø/dt2
But v= dø/dt
I= 1/R dø/dt+ 1/L. ø+c d2ø/dt2
Q2) Find V0(s)/Vi(s)?
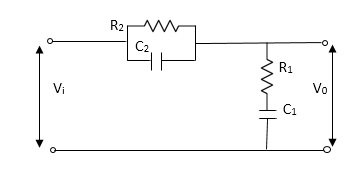
Sol: Let Z1 = R2 11 1/c2
=R2*1/c2s/R2+1/c2s
Z1= R2/1+R2c2s
Let Z2 = R1+1/c1s
Z2= 1+R1c1s/c1s
V0(s)/vi(s) = z2/z1+z2
= 1+R1c1s/c1s/R2/1+R2c2s+1+R1c1s/c1s
V0(s)/v0(s) =(c1+R1c1s) (1+R2c2s)/R2c1s+1+sR1c1s2R1R2c1c2
1.2.2 Mechanical Systems and equations of mechanical systems
1.2.2.1 Translational mechanical system:
The motion that takes place along a straight line is called translational motion. The forces that resist motion are -
Inertia: A body with mass ‘N’ acceleration ‘a’ will produce inertia fm(t)= malt N’ acceleration ‘a’ will produce inertia
fm(t)= M a(t)
In terms of velocity
Fm(t) = M dv(t)/dt
In terms of displacement
Fm(t)= Md2/dt2µt
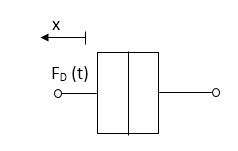Damping force: The damping force is proportional to velocity for vis case function
F0(t) = B(t) = B dx(t) /dt
B Damping coefficient N/M sec
Fig 3 Damping Force
Spring force: A spring stores potential energy. The releasing force of a string is proportional to the displacement.
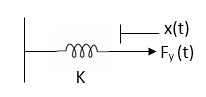Fk(t) 
x(t)
Fk(t) = k x (t)
Fk(t) = k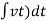 
K = string constant N/m. Fig 4 Spring Constant
1.2.2.2 Rotational mechanical system:
The motion of a body about a fixed axis is called as Rotational motion. The types of torques which can resist the motion are
Inertial Torque: - The inertial torque is the product of moment of inertia I and angular acceleration.
TI(t) = J
(t)
TI(t) = Jd/dt w(t)
TI(t) = Jd2ø(t)/dt2(N-m)
W (t) – Angular velocity
Ø(t) = Angular displacement
Damping Torque: - it is product of damping efficient B and angular velocity w
T0 (t) = B w(t)
T0(t) = B d/dt ø(t)
Spring Torque: - It is the product of torsional stiffness and angular displacement
Tø(t) = k ø(t)
K = N.m/rad
Fig 5 Spring Torque
D’Alembert’s Principle
For any body, the algebraic sum of externally applied forces and the forces resisting motion in any given direction is zero.
Ex.
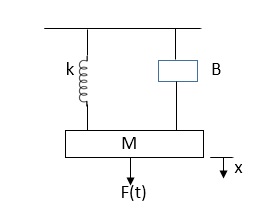
Fig 6 Mechanical System
In above figure applying D’Alembert’s principle to write the equation of motion
As force f(t) acts downwards all other forces (of k,B,x) acts Opposite to it considering f(t) as the and all other forces negative.
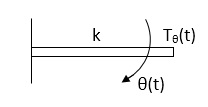
F(t)+fm (t) + fD(t) +fx(t) =0
f(t)- M d2x(t)/dt2+B dx(t)/dt +x(t)
Q.1 Draw the free body diagram and write the differential equation for system below.
Soln:- The free body diagram for M1 will be
F(t) = M1 d2/dt2x1+ B1 d/dt (x1-x2)+ k1(x1-x2)
Similarly for M2we have
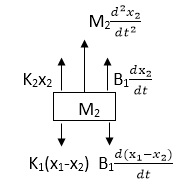
K1(x1-x2) + B1d/dt(x1-x2) = k2x2+M2d2/dt2+B2dx2/dt
Block diagrams and reduction techniques
Advantages of Block diagram reduction technique:
- Very simple to Construct the Block diagram of complicated electrical & mechanical systems.
- The function of individual element can be visualized form block diagram
- Individual as well as overall performance of the system can be studied by the figure shown in Block diag.
- Overall CLTF can be easily calculated by Block diagram reduction rules.
Disadvantages of Block diagram reduction technique:
It does not include any information above physical construct of system (completely mathematical approach). Source of energy is generally not shown in the block diagram so diff. Block diagram can be drawn for the same function.
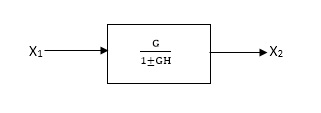
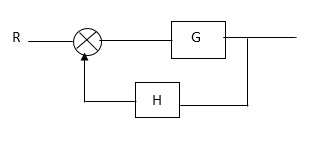
CLTf: -ve feedback
C(s)/R(s)= G(s)/1+G(s)H(s)
CLTF:-+ve feedback
C(S)/R(S) = G(S)/1-G(s)H(S)
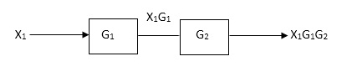
Rules of Block diagram Algebra:
Block in cascade
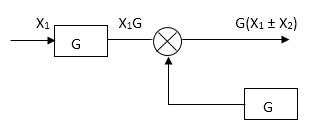Moving summing point after a block
+
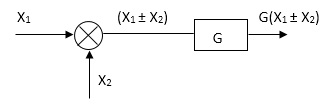
Moving summing point ahead of block
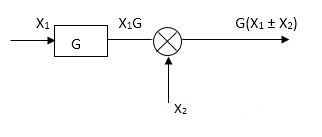
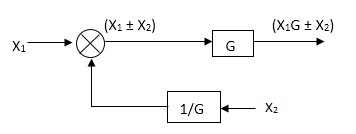
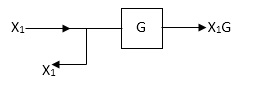
Moving take off point after a block
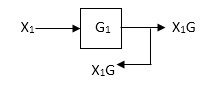
Moving take off point ahead a block
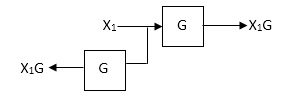
Eliminating a feedback Loop
Practice Problems
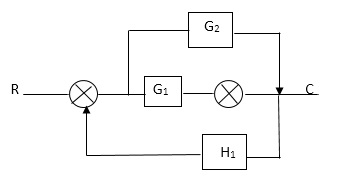
Q1. Reduce given B.D to canonical (simple form) and hence obtain the equivalent Tf = c(s)/ R(S)?
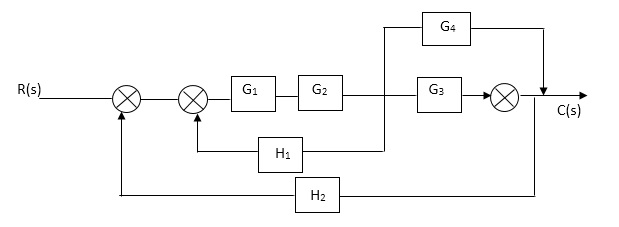
Sol:- 
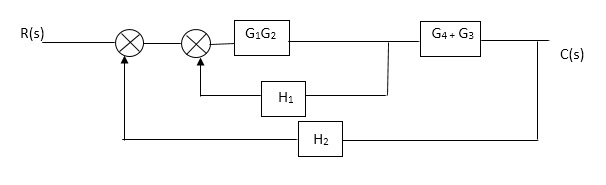
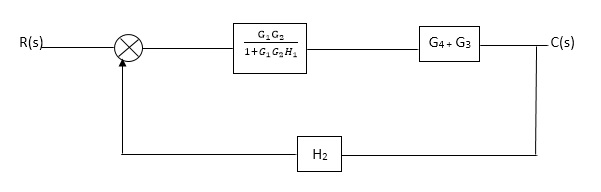
C(S)/R(S) = (G1G2) (G3+G4)/1+G1G2H1)/1-G1,G2(G3+G4) H2/1+G1G2H1
= G1G2(G3+G4)/1+G1G2H1-G1G2H2(G3+G4)
=G1G2(G3+G4)/1+(H1-H2)(G1G2) (G3+G4)
C(s)/R(S) = G1G2(G3+G4)/1+(H1-H2(G3+G4)) G1 G2
Q2) Reduce the Block diagram
Sol
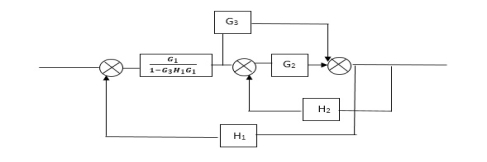
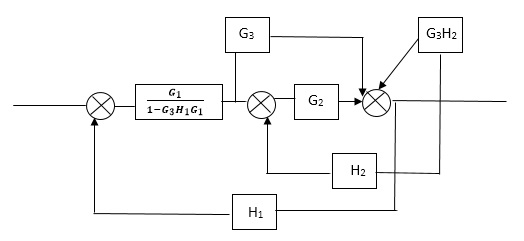
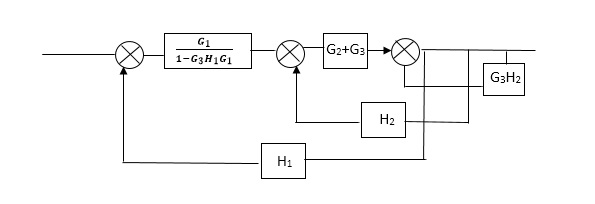
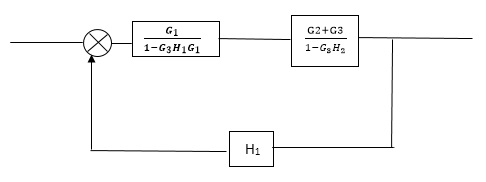
C(s)/R(s)= G1(G3+G2)/(1-G1G3X1) (1-G2X2) H1
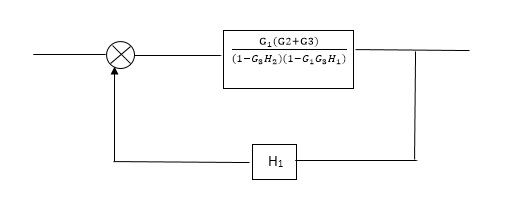
= G(G3+G2)/(1-G3G1H1) (1-G2H2) + G1H1(G3+G2)
= G1(G3+G2)/1-G3G1H1-G2H2+G1H1(G3+G2H1
=G1(G3+G2)/1-G3H2+G1G2H1(1+G3H2)
Block Diagram
SFG
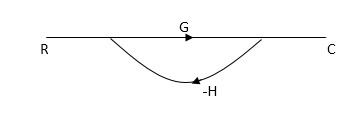
Practice Problem
Q: For given block diagram draw the SFG?
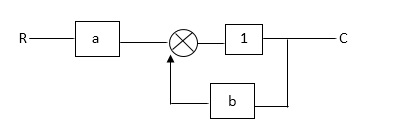
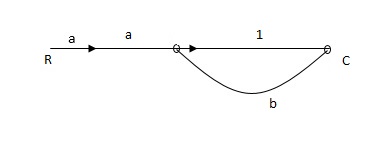
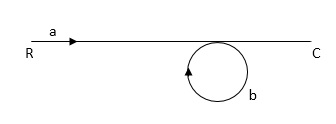
Ra+cb =c
c/R= a/1-b
RULES:-
1) The signal travels along a branch in the direction of an arrow.
2) The input signal is multiplied by the transmittance to obtain the o/p.
3) I/p signal at a node is sum of all the signals entering at that node.
4) A node transmits signal at all branches leaving that node.
Q. The SFG shown has forward path and singles isolated loop determine overall transmittance relating X3 and X1?
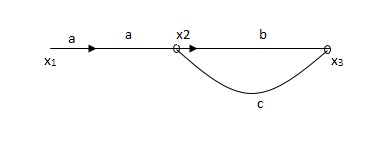
Soln:-
X1- I/p node
X2-Intenmediale node
X3- o/p node
Ab- forward path (p)
Bc- 1 loop (L)
At node XQ:
X2 = x1a + x3c [Add i/p signals at node]
At node x3:
x2b =x3
(x1a+x3c) b = x3
X1ab = x3 (1-bc)
X1 = x3 (1-bc)/ab
Ab/(1-bc) = x3/x1
T= p/1-L
X1:- I/p node x2, x3,x4,x5,Qnlexmedili node
X0:- o/p node abdeg:- forward path
Bc, ef :- Loop [isolated]
x2 = ax1+c x3
x3= bx2
x4 = d x3+f x5
x5 = e x4
x6= g x5
x6 = g(e x4) = ge [dx3+ e f x5]
xb = ge [d (bx2) + f (e x4)]
xb = ge [ db (ax1+cx3) + fe (dx3+ fx5)]
xb = ge [db (ax1+cb (ax1+x3) +fe[cdbx2]+
f( e [db (ax1+ cx3)
x2 = ax1 + cb (x2) x4 = d bx2 + f exq
x2 = ax1 + cbx2 = db (d4) + fe/1-cb
x2 = ax1/(1-cb) xy = db x2 + f x6/g
xy = db [ax1]/1-cb + f xb/g
x5 = c db ( ax1)/1-cb + efxb/g
xb = gx5
= gedb (ax1)/1-cb + g efxb/g
Xb = gx5
Gedb (ax1)/1-cb + g efxb/g
(1- gef/g) xb = gedb ax1/1-ab
Xb/x1 = gedb a/ (1- ef – bc + beef
Xb/x1 = p/ 1- (L1+L2) + L1 L2 for isolated loops
MASON’S GAIN FORMULA:
T=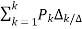 
The overall transmittance Coverall gain can be determined by Masks formula.
Explationation:-
Pk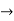
forward path transmittance of k+n path from a specified i/p node to n o/p nods
While calculating ipnode to n o/p nods.
While calculating ip no node should be encountered (used) more than ones.
it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
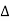= 1- [sum of all individual loop transmitting]
+ [ sum of loop transmittance product of all possible non- touching loops]
- [sum of loop transmittance of all possible triples of non- touching loops]
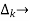path factor associated with concerned path & involves all a in the graphic which are isolated from forward path under consideration.
The path factor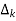 
for kth is equal to graph determinant of SFG which effect after erasing the kth path from the graph
Q. Draw SFG for given block diagram?
Sol:
P1= G1 p2 =G2 Delta1 =1
L1= -G1 H1
= 1-(-G1H1)
= 1+G1H1
T= G1+G2/1+G1H1
Q:- Determine overall gain x5 and x1 Draw SFG
X2 = ax1+ f x2
X3= bx2 +exy
X4 = cx3+hx5
X5 =dx4 + gx2
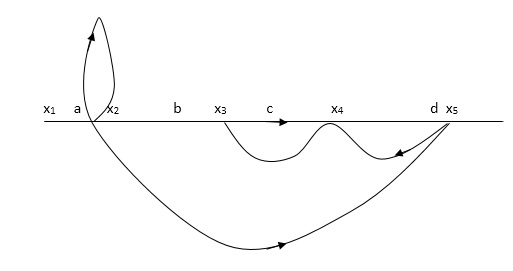
P1 = abcd p2 = ag
L1 = f L2 = ce, L3= dh
1 = 1
2= 1-ce
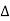= 1-[L2+L2+L3] + [L1 L2 +L1 L3]
= 1-[f+ le = dh] + [fce +fdh]
T= abcd+ ag (1-ce)/1-[ftce + dh ] + (fce + fdh)
Key takeaway
- The function of individual element can be visualized from block diagram
- The signal travels along a branch in the direction of an arrow.
- The input signal is multiplied by the transmittance to obtain the o/p.
Reference:
1 A. Ananadkumar, “Control system Engineering” PHI publication 2nd edition.
2 R. Anandanatarajan, P. Ramesh Babu , “Control Systems Engineering”, Scitech Publications .
3 John R. Hackworth,Fredrick D. Hackworth “ Programmable Logic Controller” Pearson publication.
4 I.J. Nagrath, M.Gopal “Control Systems Engineering”, 5th Edition, New Age International
