Unit 4
Kinetics of linear
Introduction
Kinetics is that branch of engineering mechanics which deals with force system which produces acceleration and resulting motion of bodies.
When body is at rest are moving in a straight line or rotating about an axis the body obeys certain laws of motion known as Newton’s law of motion.
Before discussing Newton’s law of motion let see some important terms
Mass:- the quantity of matter contained in a body is known as mass of body. Mass is scalar quantity. In SI units mass is expressed as kilogram (Kg). In CGS units it is expressed as gram (gm)
Weight:- weight of body is defined as force by which the body is attracted towards the centre of the earth.
Mathematically
Weight=mass × acceleration due to gravity
=Mass × g
SI unit for weight is Newton
CGS unit for weight is dyne
If mass is taken in kilogram and acceleration due to gravity in metre per second square then weight is expressed in Newton.
Relation between Newton and dyne:-
1 Newton=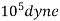
Momentum:- the product of mass of body and its velocity is known as momentum of the body.
Momentum is vector quantity
Mathematical,
Momentum=mass ×velocity
Force:- force is defined as any cause which produces or tends to produce, stops or tends to stop motion. SI unit for force is Newton.
Inertia:- it is defined as an inherent property of body which offers resistance to change of its state of rest or uniform motion.
Newton's first law of motion
Everybody continues unit state of rest or of uniform in a straight line unless it is acted upon by some external force. It is also known as law of inertia and consists of following two parts
1) A body at rest continuous in same state unless it is acted upon by some external force.
2) Body moving with a uniform velocity continues its state of uniform motion in a straight line unless it is compelled by some external force to change its state.
Note:-
1) A body at rest has a tendency to remain at rest it is called inertia of rest.
2) A body in uniform motion in straight line has a tendency to preserve its motion it is called inertia of motion.
Newton's second law of motion:-
The rate of change of momentum is directly proportional to impressed force and take place in the same direction in which force acts
This law enable us to measure force and establishes the fundamental equation of dynamics.
Consider a body moving in straight line
Lets its velocity be changed while moving
Let, m=mass of body
u=initial velocity of body
v=final velocity of body
a=constant acceleration
t=time in seconds required to change the velocity from u to v
F=force required to change velocity from u to v in t seconds.
Initial momentum=mu
Final momentum=mv
Rate of change of momentum=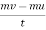
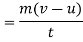
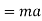
According to Newton's second law of motion the rate of change of momentum is directly proportional to impressed force
Where K is constant of proportionality
For sake of convenience the unit of force adopted is a such that it produces unit acceleration to unit mass
F=ma
=Mass × Acceleration
In a system of units unit of force is Newton written as N. Newton defined as the force while acting upon a mass of 1Kg, produces an acceleration of 1 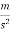 in the direction of which it acts.
in the direction of which it acts.
It is also called as law of dynamics. It is consist of following two parts.
1) A body can possess acceleration only when some of force is applied on it
i.e. if no force applied on body then there will be no acceleration and body will continue to move with existing uniform velocity.
2) the force applied on a body is proportional to product of mass of body and acceleration is produced in it.
Example 1:- determine the force which can move a body of mass 100Kg within acylation of 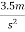
Solution:- given
m=100Kg
a=3.5 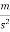
We know
Force (F) =ma
F=100×3.5
F=350N
Example 2:- a body has a 50 kg mass on the earth. Find its weight
a) On earth where g=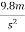
b) On moon where g=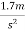
Solution:- Given
m=50Kg
Acceleration due to gravity on earth=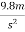
Acceleration due to gravity on moon=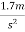
a) Weight of body on earth=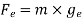
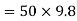

b) Weight of body on moon=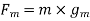
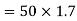
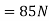
Problem 3:- A force of 100N acts on a body having a mass of 4 kg for 10 seconds. If the initial velocity of the body is 5 m/s. Determine
1) Acceleration produced in direction of force
2) Distance moved by body in a 10 seconds
Solution:- given
F=100N
t=10 sec
m=4Kg
Initial velocity=u=5m/s
1) We know
F=ma
a=F/m
=100/4
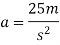
2) We know
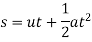
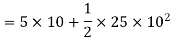
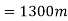
Problem 4:- A vehicle of mass 500Kg is moving with velocity of 25 m/s. A force of 200N x on 8 for 2 minutes. Find velocity of a vehicle
1) When the force acts in a direction of motion
2) When the force acts in opposite direction of motion.
Solution:- Given
m=500Kg
u=25m/s
F=200N
t=2 min
=120sec
1) Velocity of vehicle when force acts in a direction of motion
F=ma
200=500×a
A=200/500
=0.4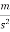
Velocity of vehicle after 120 sec
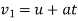
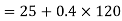
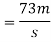
2) Velocity of vehicle when force acts in opposite direction of motion
As force acts in opposite direction of motion
a=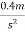 is it taken as negative.
is it taken as negative.
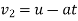
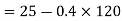
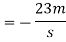
Minus sign means that vehicle is moving in opposite direction in which vehicle was moving before the force was made to act.
Problem 5:- A man of mass 60Kg dives vertically downwards and to a swimming pool from tower of height of 20 m. He was found to go down in water by 2m and then started rising. Find average resistance of water neglect the resistance of air.
Solution:- Given
m=60Kg
s=20m
Consider a motion of a man from the top of tower to water surface. In this case initial velocity (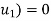
Distance covered=20m
Let 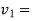 final velocity of man when he reaches water surface.
final velocity of man when he reaches water surface.
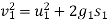
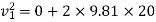
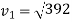
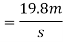
Now consider a motion of a man when he moved into water up to 2m
In this case
Initial velocity (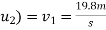
Final velocity 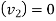
Distance covered (
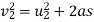
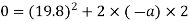
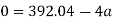
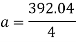
Average resistance offered by water
F=ma
=60×98.01
F=5880.6N
Motion of a lift
Consider a lift (elevator or cage etc) carrying some mass and moving with a uniform acceleration.
Let,
m=mass carried by lift
a=uniform acceleration of lift
R=Reaction of left or tension in cable supporting the lift
Consider the following two cases
● When the lift is moving upward as shown in figure 1
● When the lift is moving downward as shown in figure 2
● When lift B moving upward
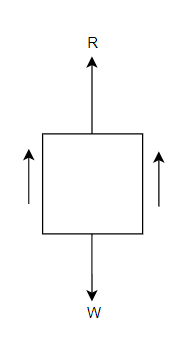
We know that downward force due to mass of le
Iift=mg
Net upward force on lift F=R-mg
We also know that this force=mass × acceleration=ma
From equation 1 and 2
R-mg=ma
R=ma + mg
R=m(a + g)
● When the lift be moving downwards :-in this case the net downward force which is responsible for the motion of lift=mg-R
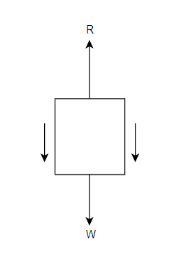
From equation 1 and 2
Ma=mg-R
R=mg-ma
R=m(g-a)
Note:-in above cases only consider mastered by lift only but sometimes examples contains mass of lift and mass carried by the lift separately.
In such cases mas carried by lift will exert a pressure on floor of lift. Where as tension in cable will be given by algebraic sum of masses of lift and mass carried by lift. Mathematically when lift is moving upward then pressure exerted by mass carried by left on its floor
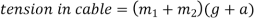

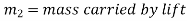
Problem 6:-In a factory and elevator be required to carry a body of mass 100 kg what will be the force exerted by the body on floor of lift when(a) lift B moving a word with retardation of 0.8(b) moving downward with retardation of 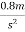
Solution:- mass of body (m) =100Kg
Acceleration (+a)=-0.8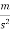 (minus sign to retardation)
(minus sign to retardation)
a) When a lift is moving upward force exerted by body on floor of the lift=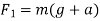
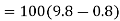

b) When a lift is moving downward force exerted by body on floor of the lift
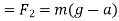
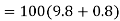
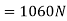
Problem 7:- an elevator of mass 500Kg is ascending with acceleration of 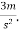 During this ascent, hits operator whose mass is 70Kg is standing on scale placed on floor. What is scale reading. What will be the total tension in cables of elevator during this motion.
During this ascent, hits operator whose mass is 70Kg is standing on scale placed on floor. What is scale reading. What will be the total tension in cables of elevator during this motion.
Solution:- mass of elevator 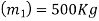
Acceleration (a)=3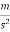
Mass of operator 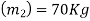
Scale reading
We know that scale reading when elevator is ascending
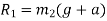
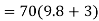
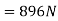
Total tension in cable of elevator when it is ascending
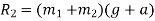
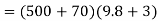
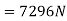
Problem 8:- an elevator of gross mass 500 kg starts moving upward with constant acceleration and acquires a velocity of 2m/s, after travelling a distance 3m. Find pull in cable during acceleration.
If elevator, when stopping moves with a constant acceleration from constant velocity of 2m/s and comes to rest in 2sec. Calculate force transmitted by a man of mass 55 kg the floor during stopping.
Solution:- given
Gross mass of elevator (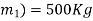
1) Pull in cable during acceleration motion
Consider a motion of elevator with constant acceleration.
Initial velocity (u)=0
Final velocity (v)=2m/s
Distance travelled=s=3m
Let
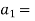 constant acceleration
constant acceleration
We know that
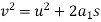
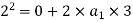
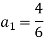
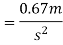
Pull required to produce this acceleration
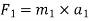
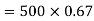

Total pull in cable=R=(500×9.8)+335
=5235N
2) Force transmitted by man during the declaration motion
Now consider motion of elevator the deceleration.
In this case initial velocity (u)=2m/s
Final velocity (v)=0
Time (t)=2s
Mass of man (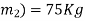
Let 
We know that final velocity of elevator is given by
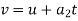
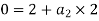
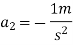
Force transmitted by man during declaring motion 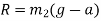
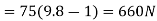
Newton's third law of motion
It states,” to every action there is always an equal and opposite reaction.”
By action is meant the force which body exerts on another and reaction means the equal and opposite force which second body exerts on first.
This law therefore state that force always occurs in pair. Each pair consisting of two equal and opposite forces.
Example:-
1) When bullet is fired from gun the bullet moves out with great velocity and reaction of bullet in opposite direction gives in pleasant shock to man holding a gun.
2) Motion of boat:- we see that boat boy always pushes the water back with help of stick which in turn boat moves forward.
Recoil of gun:-
According to the Newton’s third law of motion when bullet is fired from gun, the opposite reaction of bullet is known as recoil of gun.
Let,
M=mass of gun
V=velocity of gun with which it recoils
m=mass of bullet
v=velocity of bullet after explosion
Momentum of bullet after explosion=mv----1
Momentum of gun=MV---------2
Equating equation 1 and 2
MV=mv
This relation is properly known as law of conservation of momentum.
Example 9:- a machine gun of mass 25 kg fires A bullet of mass 30 gram with a velocity of 250 m/s. Find the velocity with which machine gun will recoil.
Solution:- given
M=25Kg
m=30gm
=0.03Kg
v=250 m/s
We know that
MV=mv
25×V=0.03×250
V=0.3m/s
Example 10:- A bullet of mass 20 gm is fired with a velocity of 300 m/s from a gun carried in carriage, which together with gun has mass of 400Kg the resistance to sliding of carriage over ice on which it rest is 20N. Find
a) Velocity with which gun will recoil
b) Distance in which it comes to rest and
c) Time taken to do
Solution:- given
m=20gm=0.02Kg
v=300m/s
M=100Kg
Resistance to sliding (F)=20N
a) Velocity with which gun will recoil
We know
MV=mv
100×V=0.02×300
V=0.06m/s
b) Distance in which it comes to rest
We know resistance to sliding (F)=20N
F=Ma
20=100×a
a=0.2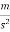
Now consider,
Initial velocity (u)=0.06m/s
Final velocity (v)=0
We also know that
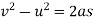
Minus sign due to retardation
0=0.06-0.2×t
t=0.3sec.
Example 11:-
A bullet of mass 10gm is a fire horizontally with a velocity of 1000m/s from a gun of mass 10Kg.
Find
a) Velocity with which gun will recoil
b) Force necessary to bring the gun to vest in 210mm
Solution:-
Given
m=10gm
=0.01Kg
v=1000m/s
M=50Kg
a) Velocity with which gun will recoil
MV=mv
50×V=0.01×1000
V=0.2m/s
b) Force necessary to be ring the gun to rest in 250mm =250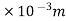
We know that
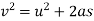
Where
u=initial velocity (u)=0.2m/s
v=final velocity (v)=0
s=displacement=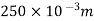
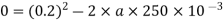
Minus sign due to retardation
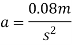
We also know that
F=Ma
=50×0.08
F=4N
Motion of boat
We see that boat boy always pushes the water back with the help of stick which in turn set a boat in motion.
When boat is at rest and both boy jump off the boat due to which boat moves background
Let,
M=mass of boat
V=velocity of boat
m=mass of boat boy
v=velocity of boat boy
Momentum of boat after boy jump=MV----1
Momentum of boat boy=mv-----2
Equating equation 1 and 2
MV=mv
Example 12:- two men standing on voting booth run in succession along its length with a speed of 4.2m/s relative to boat and drive off from the end. The weight of each mass is 80Kg and that of boat is 400Kg. If the boat was initially at rest. Find the final velocity of boat. Neglect water friction
Solution:- Given :-
v=4.2m/s
Weight of each man =80Kg
M=400Kg
Let V=velocity of booth after second Man dives off the boat
A little consideration will show that total momentum of boat is equal to momentum given by first Man plus the momentum given by second man to boat as both dives separately.
Now find momentum of boat=400×VKg.m/s
And momentum given by first man to the boat as both dives separately
Now final momentum of boat=400×VKg.m/s
And momentum given by first man to the boat
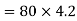
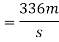
Similarly,
Momentum given by second man to the boat
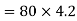

Final momentum of=momentum given first man + momentum given by 2nd man
400V=336+336
V=1.68m/s
D Alembert's principle
It states,” if a rigid body is acted upon by a system of forces, this system may be reduced to a single resultant force whose magnitude, direction and line of action may be found out by the methods of graphic statics.
From Newton's second law of motion
Force acting on body is given as
F=ma------1
Where m=mass of body
a=acceleration of body
Equation 1 can be written as
F-ma=0------2
It may be noted that equation 1 is equation of dynamics whereas equation 2 is equation of statics.
Equation 2 it is also known as equation of dynamic equilibrium under the action of real force F.
This principle is known as D Alembert’s principle
Example 13:- Two bodies A and B of mass 80 kg and 20 kg are connected by thread and move along a rough surface under the action of force 400KN applied to first body of mass 80 kg as shown in figure 3.
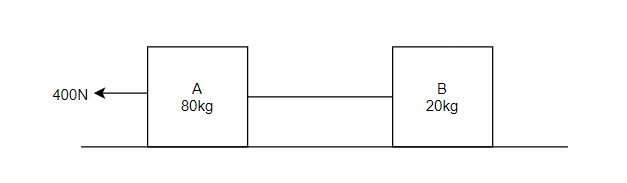
The coefficient of friction between sliding surface of bodies and surface is 0.3. Determine the acceleration of two bodies and tension in thread using D Alembert’s principle
Solution:- 
P=400N
=0.3
1) Acceleration of two bodies
Let a=acceleration of bodies
T=tension in thread
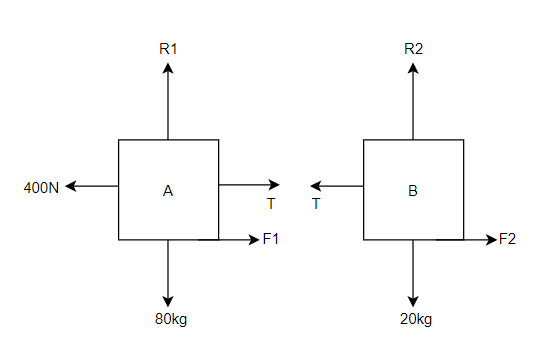


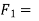
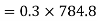
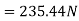
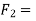
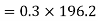
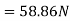
Consider body A
Resultant horizontal force
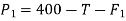
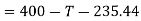
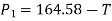
Force causing acceleration to body A=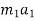
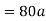
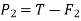
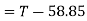
Force causing acceleration to body B=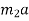
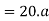
According to D Alembert’s principle
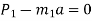
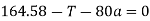


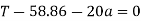
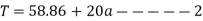
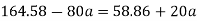

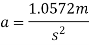
2) Tension in string

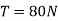
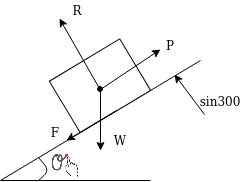
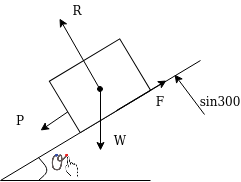
Motion on inclined planes
Consider a body moving downward on inclined plane as shown in figure 5
Let
m=mass of body
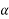 =Puclination of plane
=Puclination of plane
We know
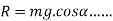 reaction force
reaction force
 ……..Friction Force
……..Friction Force
Consider a body as shown in figure 19 subjected to force 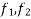 and moving with acceleration in x axis.
and moving with acceleration in x axis.
 Let u=initial velocity at
Let u=initial velocity at
v =find a velocity at B
When it moves distance AB=S
Then resultant of system of forces must be in X direction
Let 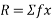
From Newton's second law of motion
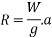
Multiplying both sides by elementary students ds we get
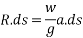
= 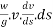
=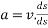
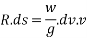
Integrating both sides for motion from A to B we get
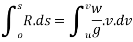
Example 23:--A horse pulling a cart exerts a steady horizontal pull of 300N walks at a rate of 4.5 km/h .how much work done by whom in 5 minutes.
Solution:- Given
Force=f= 300N
V=4.5km/h
=75m/min.
Distance travel in 5 minute=75×5
=375m
We know ,
Work done = force × displacement
Work done by horse=300×375
=112.5×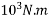
=112.5kN.m
=112.5kJ
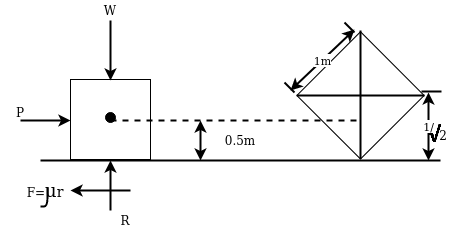
Example 24:-A man wishes to move wooden box of 1m cube to a distance of 5 M with least amount of work if block weights 1 KN and coefficient of friction is 0.3 find whether we should tip it or slide
 Solution:-Given
Solution:-Given
Weigh of box=W=1KN
Displacement=5=5m
Friction=u=0.3
Work done in sliding
For sliding
Applied force (p) = frictional force
Frictional force=u.R
=0.3×1
=0.3KN
Applied force=0.3KN
Work done=force×displacement
=0.3×5
=1.5 KN.m=1.5J
Work done in tipping
In one tipping centre of gravity of box to be raised to heights =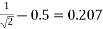
Work done in one tipping=5×0.207
=1.0355kj
Work done in sliding>work done in tipping
Men should move the box by the tipping
- Energy:-energy is defined as capacity to do work there are many forms of energy like heat energy mechanical energy to electrical energy and chemical energy. In engineering mechanics are interested in mechanical energy this energy is classified into
- Potential energy
- Kinetic energy
Potential energy:-potential energy is the capacity to do work due to position of body consider a body of weight W held at height h possesses an energy Wh .
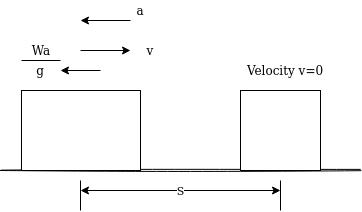
Kinetic energy:-kinetic energy is the capacity to do work due to motion of body consider a car moving with velocity v m/sec if engine is stopped but it still moves forward doing work against frictional resistance and stops at certain distance s from kinematics of motion
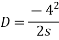
 From
From 


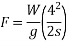
Work done=F.S
=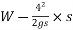
=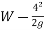
This work done by energy stored initially in the body.
Kinetic energy=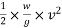
When v= velocity of the body
- Unit of energy:-unit of energy is same as that of work since it is nothing but capacity to do work it is measured in in joules (N.m) .
- Work energy principle:-consider a body as shown in figure 19 subjected to force
And moving with acceleration a in X direction
Let
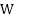 U = initial velocity at A
U = initial velocity at A
V= final velocity at B
When it moves distance Ab=s
Then resultant of system of force must be in X direction.
From Newton's second law of motion

Multiplying both sides by elementary distance ds we get.
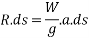

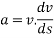
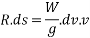
Integrating both sides from motion from a to b we get

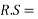

Now R.S=work done by a force is acting on body
=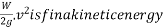
=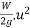 Is initial kinetic energy
Is initial kinetic energy
Hence we can say that work done in a motion is equal to change in kinetic energy mathematically
Work done=final kinetic energy-initial kinetic energy and it is called work energy equation
This work-energy principle may be states,” The work done by a system of forces acting on a body during a displacement is equal to change kinetic energy of body during same displacement.”
Note:-this method is advantages over D Alembert’s method when problem involves velocities rather than acceleration
Example 25:-A body weighing 300N is pushed up 30° plane by 400N force acting parallel to plane. If initial velocity is 1.5m/s and coefficient of friction is 0.2 what velocity when body have after moving 6m .
Solution:- Given
Weight of body=w=300N
Applied force = p= 400N
Initial velocity=v=1.5m/s
Displacement=s= 6m
Co-efficient of friction=u= 0.2
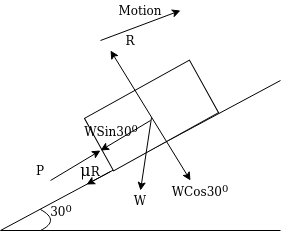 Q=30°
Q=30°
Frictional force=F= u.R
Where R = reaction force=w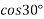
=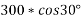
=259.80N
Frictional force=0.2×259.80
=51.9615
Let V= final velocity
According to work energy principle
Work done= change in kinetic energy
(Total force)×displacement=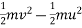
=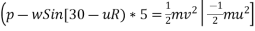
=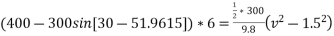
V=8.9376m/s
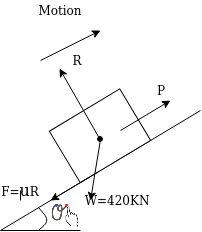
Example 26:- find the power of a locomotive drawing a train whose weight including that of engine in 420 kN ab and inclined in 120 at a steady speed of 56 km/h frictional resistance during 5N/KN while train is a a sending the incline the steam is shut off find how far it will move before coming to rest assuming that the resistance to motion remain same.
 Solution:-
Solution:-
V=56km/h
=15.56m/s
F=5×420
=2100N
F=2.1KN
P=F+W
=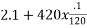
=5.5KN
Power of locomotive=work done by p per second
=P×distance moved per second
P×v
5.6×15.56
87.11KN
When steam is put off Let It move a distance s before coming to rest.
Initial velocity=16.56m/s
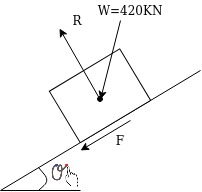 Final velocity=v=0
Final velocity=v=0
W=420KN
Figure shows the system of forces acting in this motion
Resultant force parallel to plane=
=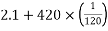
5.6KN (down the plane)
According to work energy principle
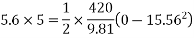
S= 924.98m.
- Power:-the power may be defined as the rate of doing work in SI unit system unit of power is watt(w) which equals to 1 Nm/s or 1 j/s .
- Types of engine power
- Indicated power
- Power brake
- Indicated power (I.p):-the actual power generated in engine cylinder is cold indicated power it is also defined as power which is feed into engine in the form of steam or colorific value of the fuel.
- Brake power (B.P):-it is observed that entire power generated by engine cylinder is not available for useful work some of the power is used utilised in overcoming internal friction of moving parts of engine the net output of enginei.e I.P -losses is called break power
- Efficiency of an engine (mechanical efficiency):-it is defined as a ratio of great power to indicated power
Mathematically
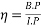
Example 27:-a tram car weighs 120KN tractive resistance being 5N/KN. What power will be required to propel the car at a uniform speed of 20km/h.
- On level surface
- Up an incline of line 300.
- Down an inclined of Lin 300
Take efficiency of motor as 80%.
Solution:- on level track
Locomotive is moving with uniform velocity hence it is equilibrium, v= 20km/h =5.556m/d
Frictional resistance=5N/KN.
=5×120
=600N
=0.6KN
P=F=0.6KN
Output power =P.V
=0.6× 5.556
=3.333KN
=
Input power=
=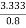
=4.167 kwatt
- Up the plane
=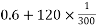
=1KN
Output power required=p×v
=1×5.556
=5.556KW
Input power of engine=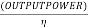
=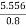
=6.9kw
- Down the plane
P=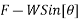
=0.6-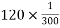
0.2
Output power=0.2×5.556
=1.1111Kw
Input power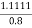
=1.389kw
- Motion of connected bodies:-work energy principle can also apply to connected bodies there is no need to separate connected bodies and work out for forces is connected member equate summation of work done by forces acting on bodies to summation of change in kinetic energy of bodies consider two bodies connected to each other as shown in figure 20.
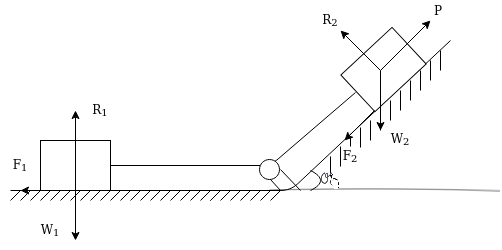
Under pull p both bodies move the same distance and with same velocity hence initial velocity final velocity and displacement are same for two bodies out of three forces acting on first body only the frictional force
acting on first body only the frictional force  will do work forces acting on second body the applied force P frictional force
will do work forces acting on second body the applied force P frictional force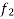 and down plane component of weight
and down plane component of weight 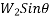 will do the work hence work energy equation for system will be
will do the work hence work energy equation for system will be
=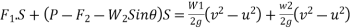
=
Example 28:-in what distance will body A of figure 21 attain velocity of 3m/s starting from rest
Block a weights=1500N
Block B weights=200N
U=0.2
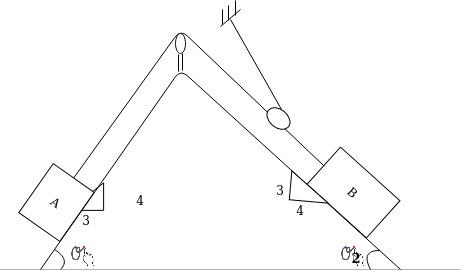
Solution:-

Let 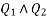 be the shopes of inclined plane
be the shopes of inclined plane
Then 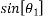 =4/5
=4/5
 =3/5
=3/5

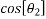 =0.8
=0.8
By observing pulley system it may be conclude that if 1500N body moves a distance ‘s' 2000N body moves distance 0.55 and if velocity of 1500N blocks is we then velocity of block 2010 is 0.5 V as human 2000N body moves up the plane and block 1500N moves down the plane.
Forces acting on block 1500N that will do work.
.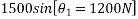 down the plan
down the plan
.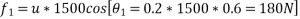 up the plan
up the plan
The force acting on block 2000N that will do work
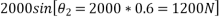 down the plan
down the plan
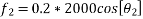
=320N(down the plane)
Applying work energy principle
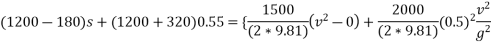
In this case
V=3m/s
260s=
S=3.529m.
Work done by spring:-considering body attached to Spring as shown in figure 2
If a body moves out from its undeformed position then cancel force is develops. If a body moves towards support compressive force develop.
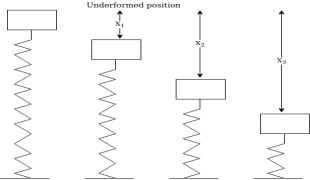
In other words the force of a spring is always directed towards its normal position experimental results show that magnitude of force develop in Spring is directly proportional to its displacement from undeformed position Thus if F is the force in Spring due to the formation X from its undeformed position.
Then
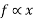
F=kx
Where k= spring constant and is defined as a force required for unit the formation of spring
Unit of spring constant is N/m
At any instant if displacement is dx work done by spring force du is given by
Du=-Fdx
=-kx.dx
Negative sign is used to indicate that force of spring is in opposite direction of displacement
Work done in displacement of body from  to is given by
to is given by
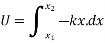
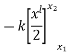
=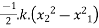
If work done is to be found in moving from an underformed position to displacement.
Then 
=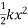
- Note:-the negative sign is used with expression for work done by spring since when ever spring is the form the force of spring is in opposite direction of the formation however if a deformed spring is allowed to moved towards its normal position work done will be positive sense the movement and force offspring are in same direction.
Example 29:- A 3000N block starting from rest as shown in figure 23 slide down a 50° incline after moving to M it strike a spring whose modulus is is 20N/mm if coefficient of friction between block and plane is 0.2 determine maximum the formation of the spring and maximum velocity of block.
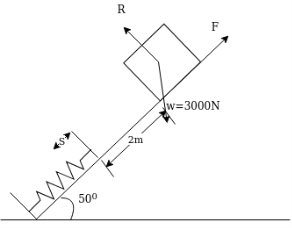 Solution:-Normal reaction =R=
Solution:-Normal reaction =R=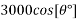
=1928.3628N
Frictional force=R×u
=1928.3628×0.2
Frictional force=F=385.6726N
Let maximum the formation of spring is S mm. The body is at rest and is again at rest when it moves (2000+5)mm
Applying work energy principle

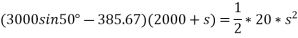
(191.246) (2000+s) =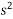
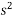 -191.246.5-382492=0
-191.246.5-382492=0
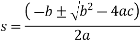
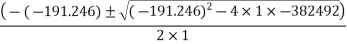
s=721.4311mm
The velocity will be maximum when acceleration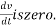
Acceleration is zero when force is zero net force acting on body is zero when spring force developed balances the forces is exerted by body let x be deformation when net force on body in direction of motion is zero.
 Referring to fig 24.
Referring to fig 24.
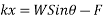
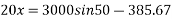
x=95.62mm
Now applying work energy principle
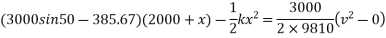
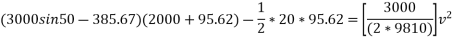
V=5060.9 mm/sec
V = 5.0609 m/s
Note:- g=9.81m/s
g= 9810mm/s
- Linear impulse and momentum.
If R is the resultant force acting on a body of mass M then according to Newton's second law of motion
R=ma.
But acceleration= a =
R= 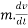
Rdt=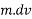
Integrating on both sides
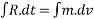
If u=initial velocity
V= final velocity after time interval t
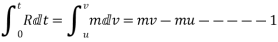
The term 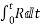 is called Impulse if r is in Newton and time is in second then unit of impulse is N second .if R is constant during time interval t then impulse=R×t
is called Impulse if r is in Newton and time is in second then unit of impulse is N second .if R is constant during time interval t then impulse=R×t
The term mass ×velocity is called momentum.
Now 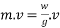
Substituting dimensional equivalence
=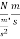
=N.sec
Thus unit of momentum is also N sec.
Equation (1) can be written as
Impulse= final momentum-initial momentum
Since velocity is vector, impulse is also vector equation (2) is known as impulse momentum equation holds good then direction of R, u and v are in same.
Impulse- momentum equation can be stated as follow:-
“the component of resultant linear impulse along any direction is equal to change in component of momentum is that direction.”
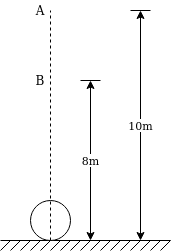
Example 30:-A glass marble vs 0.2 n falls from height of 10m and rebounds to a height of 8 M find impulse and average force between the marble and floor if time during which they are in contact is 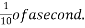
Solution:-Applying kinematic equation for freely falling body the velocity with which marble strike the floor.
=
=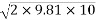
=14.007m/s (downward )
Similarly marble moving up
Velocity of rebound=
=12.528m/s (upward)
Taking off a direction as positive and applying impulse momentum equation
 Impulse=
Impulse=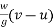
Impulse=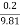
=0.541N sec
If f is average force then
 =0.541
=0.541
F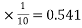
F= 5.41 N
Example 31:-A block wing 130 N is on incline whose shape is 5 vertical to 12 horizontal. Its initial velocity down the incline is 2.4 m/sec. What will be its velocity 5sec later take coefficient of friction at contacts =0.3
Solution:-
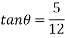
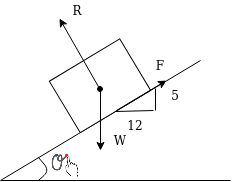
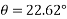
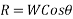
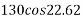
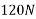
Frictional force=f=120×0.3
=36N
Forces down the plane =R=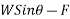
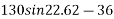
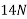
Initial velocity=u=2.4m/s
Final velocity=v=m/s
Time interval=t=5sec
Applied impulse momentum equation

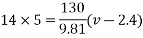
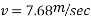
- Connected bodies:-problem involving connected bodies may be solved by any one of following two methods
First method:-free body diagram of each body is drawn separately impulse momentum equation for each body in direction of its motion is written and then equations are solved to get required values.
Second method:-if the connected bodies have same displacement in same time the Impulse of internal tension is connected chords will get cancelled his free body diagram of combined bodies mein been considered and impulse moment equation applied in direction of motion of combined bodies
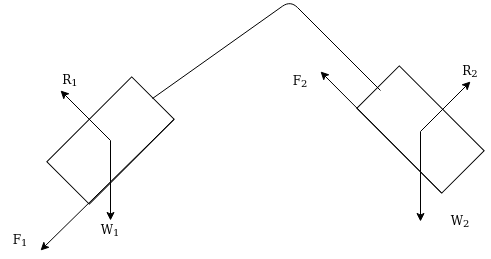
Example 32:-determine time required for weights shown in figure 24 to attain velocity of 98m/sec what is tension in chord take u=0.2 for both planes assume pulleys as frictionless.
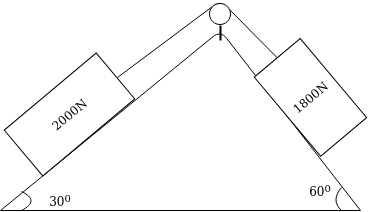
Solution:-1st method
F.B.D for 2000N block
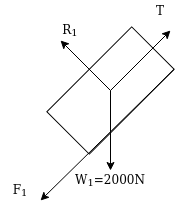
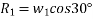
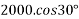
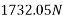
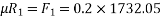
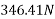
FBD for 1800N block
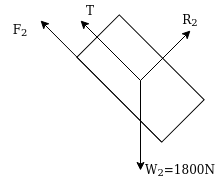
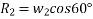

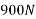
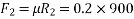
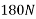
Let T = tension in chord
Initial velocity=u=0
Final velocity=v=9.81m/s
Applying impulse momentum equation for 2000N block in our direction parallel to plane
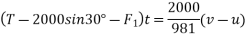

Applying impulse momentum equation from 1800N block in downward direction parallel to 60° inclined plane.
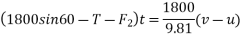
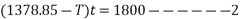
Equation 1 divide 2
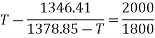
T=1363.48
Substituting it in equation 2
(1378.85-1363.48)t =1800
= 117.11 sec
- Second method:-since displacement is same for both bodies in given time consider combined FBD for blocks.
Applying impulse momentum equation in direction of motion
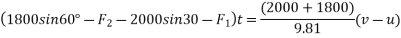
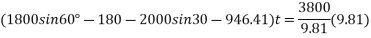
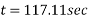
To find tension in chord
Consider b is impulse momentum equation for anyone blog say 2000N block.
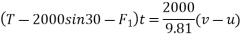
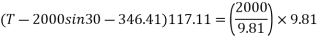
T=1363.48N
- Pile and pile hammer:- if the safe bearing capacity of soil is to lease a set of rain forced or steel poles are driven in the soil such poles are known as piles over the group of pile concrete cap is coast and on its structure is built pile and driven by pile hammer it consists of a movable weight call hammer as shown in figure 25
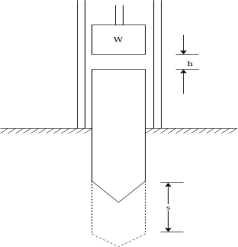
The hammer is raised to certain height h and finally dropped it is died due to fall over a pile after Hamal strikes the pile the hammer and pile moves downward together the kinetic energy of pile and hammer is utilized in doing work against resistance of ground and pile get 7 by distance S if distance moved by blow in second earth resistance can be calculated.
Example 33:- A pile of weight W is driven vertically through a distance S when a hammer of weight W is dropped from height h calculate average resistance of the ground the loss of kinetic energy during the impact and time during which pile is in motion
Solution:- initial velocity of hammer:- 0
Distance moved before striking pile:-h m
Gravitational acceleration :-g 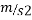
Velocity of hammer while striking pipe V B given by
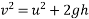
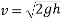
After striking the hammer and pile moves together hands momentum is conserved applying principle of conservation of momentum
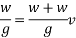
Where v= velocity of hammer and file immediately after the strike
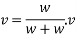
With this initial velocity the pile and hammer start moving downward and they stop moving after a distance S during this process work is done against resistance R of earth.
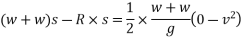
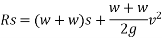
From 2 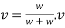
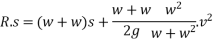
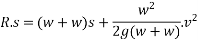
From 1 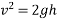
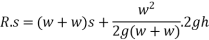

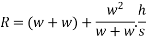
Loss of kinetic energy during impact
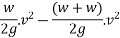



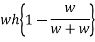
Loss of K.E=
Time during which pile is in motion
Let t be the time during which the pile is in motion applying impulse - moment equation
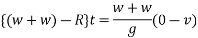
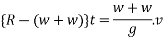
Substituting for R and v
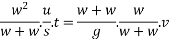
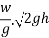
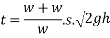
Example 33:-a pile hammer wing 20k and dropped from height of 750 mm on a pile of 10k N the pile penetrates 100mm/blow assuming that the motion of pile is resisted by a constant force find the resistance to penetration off ground.
Solution:-initial velocity of hammer=u=0
Distance moved=h=750mm=0.75m
Acceleration=g=9.81
Velocity at time of strike:-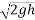
=
=3.836m/s
Applying principle of conservation of momentum of pile and hammer we get velocity V of pile and hammer after impact.
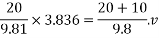
V=2.557m/s
Applying work energy equation to motion of hammer and pile
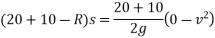
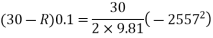
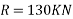
Reference Books
1.Engineering Mechanics by S. S. Bhavikattis, New Age International Pvt. Ltd.
2.Engineering Mechanics by R. K. Bansal and Sanjay Bansal.
3.Vector Mechanics for Engineers Vol.I and II by F. P. Beer and E. R. Johnston, Tata Mc-Graw Hill Publication.
4.Engineering Mechanics by Manoj K Harbola, Cengage Learning
5.Engineering Mechanics by K. I. Kumar, Tata Mc-Graw Hill Publication
6.Engineering Mechanics by S. B. Junnerkar.
7.Engineering Mechanics by Irving H. Shames, Prentice Hall of India, New Delhi.
8.Applied Mechanics by S. N. Saluja, Satya Prakashan, New Delhi.
9.Engineering Mechanics by Statics and Dynamics by Ferdinand Singer, Harper and Row Publications
10.Engineering Mechanics by R. S. Khurmi, S. Chand Publications
11.Fundamentals of Engineering Mechanics by S. Rajasekaran, G. Sankarasubramanian,VikasPublishing House
12) “Applied Mechanics- Dynamics &Statics ” by I.B.Prasad, Khanna Publisher, Delhi