Unit 5
Kinetics of circular motion
Introduction
The motion of a body along a circular path is known as circular motion. In circular motion the centre of rotation remains fixed. The examples of body is moving in a circular path are shafts, flywheel, pulleys etc. Rotating about their geometric axis.
Angular velocity
It is defined as rate of change of angular displacement of body. It is denoted by 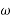 .
.
Angular displacement is always measured in terms of angle covered by body from initial position.
Consider a body moving along a circular path as shown in figure 1
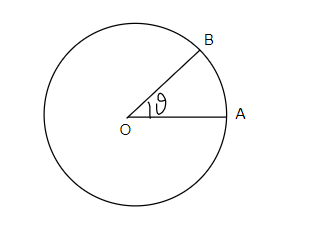
Consider a body initially at position A and after time t body moves to position B.
Let
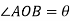
Angular displacement=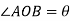
Time taken=t
Angular velocity=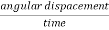

Mathematically
Angular velocity=
Angular velocity is expressed in terms of revolutions describe in one minutes.
Example if at an instant angular velocity of rotating body in N r.p.m. (i.e. revolutions per minute) the corresponding angular velocity (in radians) may found out as discussed below
One revolution/min=2πrad/min
N revolution/min=2πN rad/min
Angular velocity= 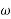 =2πN rad/min
=2πN rad/min
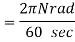
Relation between linear velocity and angular velocity
Consider a body moving in circle as shown in figure 1
Initial position of a body is at A. And after time t body moves to position B
Let
Angular velocity=
Let
v=linear velocity=
Linear displacement=arc AB
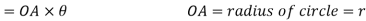
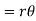
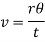
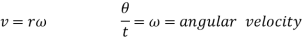
Angular acceleration:-
It is defined as the rate of change of angular velocity. It is measured as radians per second hand written as 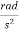
It is denoted as 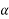
Mathematically,
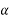 =Rate of change of angular velocity
=Rate of change of angular velocity
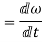
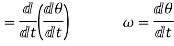
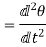
Also,
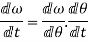
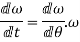
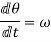
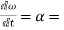 angular acceleration
angular acceleration

Relation between linear acceleration and angular acceleration
We know that
Differentiating above equation with respect to t
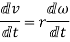
But 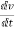 =Linear acceleration=a
=Linear acceleration=a
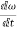 =angular acceleration=
=angular acceleration=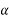

Linear acceleration is equal to r times the angular acceleration
Equations of motion along circular path consider a body which is moving along a circular path
Let
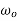 =Initial angular velocity of body in radians per second
=Initial angular velocity of body in radians per second
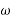 =Final angular velocity of body in radians per second
=Final angular velocity of body in radians per second
t=time in second during which angular velocity changes from
 =Angular displacement in radians
=Angular displacement in radians
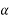 =Angular acceleration in
=Angular acceleration in 
We know that
 =Rate of change of angular velocity
=Rate of change of angular velocity
=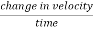
=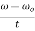
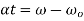

We know that
Average angular velocity=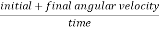
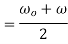
Angular displacement= 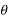 =average angular velocity×time
=average angular velocity×time
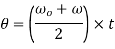
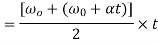
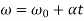
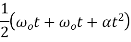
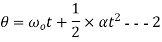
Final angular velocity 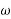 is given by
is given by
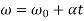
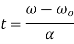
Angular displacement 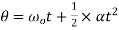
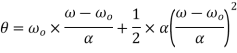
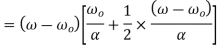
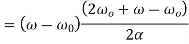
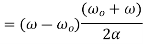
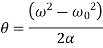
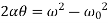
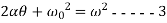
Relation between linear motion and angular motion
SR.No. | Particulars | Linear Motion | Angular Motion |
1 | Initial velocity | u | 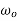 |
2 | Final velocity | v | 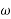 |
3 | Constant acceleration | a | 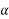 |
4 | Total distance traversed | s |  |
5 | Formula for final velocity | v=u+at | 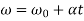 |
6 | Formula for distance traversed | 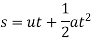 | 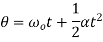 |
7 | Formula for final velocity |  | 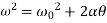 |
8 | Differential formula for velocity | 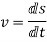 | 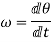 |
9 | Differential formula for acceleration | 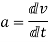 | 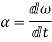 |
Motion of rotation of a body under variable angular acceleration
We discussed the motion under constant acceleration but in actual practice it is seldom possible that body move with constant acceleration i.e. rate of change of velocity is constant at t times.
A body which does not move with constant acceleration is said to be moving with non uniform or variable acceleration.
Angular velocity and angular acceleration at any instant

Consider a body moving in circular motion from position A to position B in time t second
Let
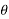 =Angular displacement in radians
=Angular displacement in radians
t=Time taken by body to move from porition A to B
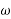 =Angular velocity
=Angular velocity
 =Angular acceleration
=Angular acceleration
We know that,
Angular velocity is the rate of change of angular displacement of a body.
Mathematically,
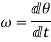
Similarly,
Angular acceleration is rate of change of angular velocity of a body.
Mathematically
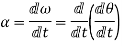
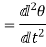
Also
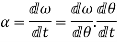

Methods for angular velocity, angular acceleration and angular displacement from mathematical expression
Angular velocity and angular acceleration and angular displacement from mathematical expression may be found out by either of following two methods
1) By differentiation
2) By integration
Angular velocity and angular acceleration by differentiation
Sometimes the given equation of motion is in terms of angular displacement and time t.
Example:-
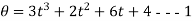
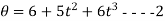
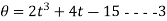
Mow, differentiating both sides of equations w.r.t. t
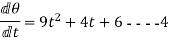
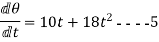
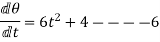
The equations so obtained by differentiation give angular velocity of the body.
Again differentiating both sides of above equations
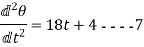
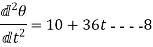
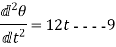
The equations so obtained by second differentiation gives angular acceleration of the body.
By integration:- by integration the given angular acceleration equation gives angular velocity and again integrating gives angular displacement.
Centripetal acceleration
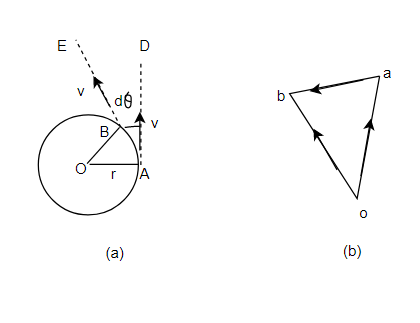
Consider a particle moving along the circumference of a circle with  as a centre as shown in figure 3(a)
as a centre as shown in figure 3(a)
Let
r=radius of a circular path in m
v=linear velocity of particle in m/s
Now consider and instant when A the position of particle. After a small interval of time. Let its portion is changed from A to B. When body is had a its linear velocity will be along dotted line AD. i.e tangent at A. Similarly when body is at B its linear velocity (again equal to v) will be along the dotted line BE i.e. tangent at B as shown in figure 3 a
First of all, take any suitable point O draw on parallel to AD and let it represent the velocity v at A in a direction and magnitude to same scale. Similarly draw ob parallel to BE let it represent the velocity v at B in a direction and magnitude to scale join ab as shown in figure to 2 b
Now in triangle oab, oa represents initial velocity, ob represent final velocity and AB represent change in velocity
We know,
Acceleration=a=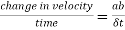
Since 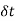 is considered to be very small
is considered to be very small
Therefore chord AB may be considered to be equal to arc AB. Now consider two triangles AOB and aob which are similar.
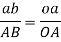
Substituting values of AB= 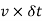 , oa=v and OA=r in above equation
, oa=v and OA=r in above equation
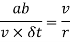
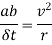


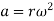
Note:- The same formula holds good for centrifugal acceleration also.
Centripetal force:-
A body moving in circle or along a circular path with constant velocity suffers a continuous change in its direction at every point of its motion but magnitude of its speed remains constant since velocity is vector quantity i.e. magnitude and direction both are considered and velocity of body is continuously changing due to change in direction; therefore according to Newton’s first law of motion an external force must act continuously upon body to produce a change in direction of moving body.
Due to inertia body tends to move along the tangent at every point of its motion with constant velocity. Therefore some force must act at right angles to direction of motion at every point, which should be change the direction of motion of body leaving speed uniform.
Thus the force which act along radius of circle at every point and is always directed towards centre of circle along which body moves is known as centripetal force.
Centrifugal force:-
According to Newton’s third law of motion, the force which acts opposite to centripetal force is known as centrifugal force.
Centrifugal force always acts away from centre of path i.e. centrifugal force always tends to throw the body away from centre of circular path.
Example 1:- A stone of mass 1 kg is revolving in circle of radius 1m with linear velocity of 10m/s what is value of centrifugal force acting on the stone.
Solution:-
Given
m=1Kg
v=10m/s
r=1m
We know
Centrifugal force acting on the stone 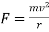
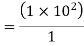
Example 2:- A ball of mass 0.25Kg is attached to end of 2m long string. The string will break if tension in string is more than 25N. What is the maximum angular velocity at which a ball can be rotated.
Solution:- given
m=0.25Kg
r=2m
F=25N
Centrifugal force 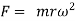
(tension in string)
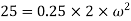
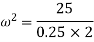
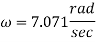
Example 3:- a body of mass 0.5Kg tied to string is whirled in vertical circle working 2 rev/sec. If radius of circle is 1.2m, then find tension in string when body is at top.
Solution:- given
m=0.5Kg
Angular rotation (N)=2 rev/sec
r=1.2m
1) Tension in the string when body is at top
Angular velocity= =2πN
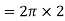

Tension in string 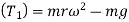
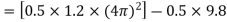
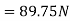
2) Tension in string when body is at bottom
Tension in string 
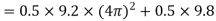
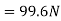
Centrifugal force acting on a body moving along a circular path
Consider a body moving along a circular path with constant velocity
Let
m=mass of body
r=radius of circular path
v=linear velocity of body
We know,
Centrifugal acceleration of body=a=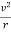
And
Centrifugal force  mass× centrifugal acceleration
mass× centrifugal acceleration
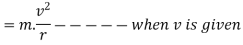
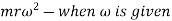
Example 4:- an automobile of mass 1.5t, travelling at of 54Km/hr traverses a sag in the road. The sag is part of circle of radius 25m. Find the reaction between automobile and road while travelling at lowest part of the sag.
Solution:-
Given
Mass of automobile (m)=1.5t

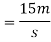
Radius of sag (r)=25m
We know that reaction between automobile and road while travelling at lowest part of sag
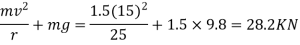
Equilibrium of vehicle moving along a level circular path
We have seen that outer edge of road is always raised for circular turn. This is known as banking of road. Similarly, whenever alignment of railway takes circular turn outer rail is raised by an amount equal to super elevation then inner rail. The main idea of banking of road or super elevation in railway line is to distribute the load of vehicle equally on both wheels.
But if roads are not banked then a vehicle may have to face following miss happenings. This will also happen when vehicle moves with a velocity more than permissible velocity.
1) Vehicle may overtone
2) Vehicle may skid away.
Maximum velocity to avoid over it earning of vehicle moving along a level circular path
Consider a vehicle moving on a level circular path with O as a centre as shown in figure 4
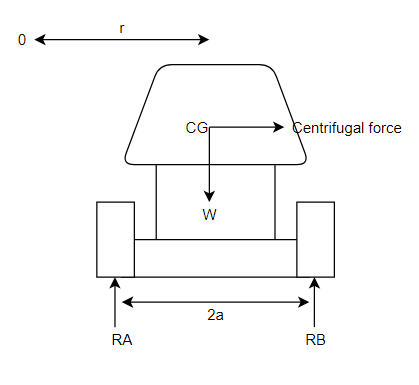
Let
m=mass of vehicle
v=velocity of vehicle
r=radius of circular path in m.
h=height of C.G. Of vehicle from ground level in m.
2a=distance between reactions A and B
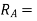 reaction at A
reaction at A
 =reaction at B
=reaction at B
We know that centrifugal force acting through C.G. Of vehicle
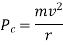
Also
Weight of vehicle=mg acting downward through its centre of gravity will exert reaction equal to 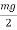 on A and B (because of symmetry) taking moment about A and equating the same
on A and B (because of symmetry) taking moment about A and equating the same
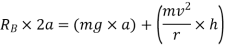

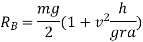
Similarly by taking moment about B and equating the same we get
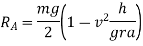
Little consideration will show that reaction at B. I.e.  can never be negative. But reaction at A i.e.
can never be negative. But reaction at A i.e. 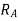 can be negative if value of
can be negative if value of  becomes more than unity if we observe
becomes more than unity if we observe  we can say that
we can say that 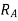 can be negative if value of v is increase, all other things are constant.
can be negative if value of v is increase, all other things are constant.
When this condition reaches, the vehicle will overturn at wheel B. Therefore in order to avoid overturning
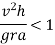
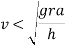
In order to avoid overturning velocity of vehicle is less than that obtained from above equation the vehicle will not overturn if velocity is more vehicle is bound to overturn.
Therefore to avoid overturn maximum velocity is given
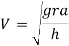
Note:- From above equation we say that maximum velocity of vehicle to avoid overturn is independent of its mass.
Example 5:- A vehicle weighing 1 tonnes is to turn on a circular curve of 40 m radius. The height of its C.G. Above road level is 75cm and distance between the centre lines of wheels is 120cm. Find speed at which vehicle should be run in order to avoid overturning.
Solution:-
Given
M=1 tonnes
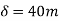
h=75cm=0.75m
2a=120cm=1.2m
a=0.6m
We know maximum speed at which vehicle should to run in order to avoid overturning
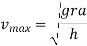
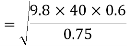
=17.7m/s
63.72 Km/hr
Example 6:- Racing motor car is negotiating a curve of radius 50m. The distance between the centre to centre of wheel is 1.5m and height of C.G. Of car is 90cm above the ground level, find maximum speed of motor to avoid overturning.
Solution:- given
r=50m
2a=1.5m
a=0.75m
h=90cm
=0.9m
We know
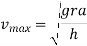
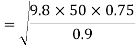
=20.21m/s
=72.78 km/hr
Maximum velocity to avoid skidding away of vehicle moving along a level of circular path
Consider a vehicle moving on a level circular path with O as shown in figure 4
Let
m=mass of vehicle
v=velocity of vehicle
r=radius of circular path in in m.
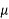 =Coefficient of friction between the wheels of vehicle and ground
=Coefficient of friction between the wheels of vehicle and ground
We know that,
Centrifugal force which tends to skid away the vehicle
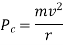
And friction force between the wheels of vehicle and ground

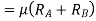
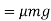
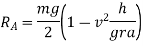
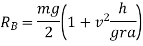
The skidding away can only be avoiding if frictional force is more than centrifugal force. Therefore in order to avoid skidding away.
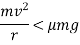
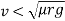
It is thus obvious that if velocity is less than that obtained from above equation, the vehicle will not skid away. But velocity is more than that of obtain from above equation, vehicle will skid away.
Therefore, in order to avoid skidding maximum velocity

Note:- From above equation we can say that maximum velocity of vehicle to avoid skidding is independent of its mass.
Example 7:- A car is travelling on a level track of radius 50m find maximum speed at which he can travel as curved truck. If coefficient of friction between tires and track is 0.45. Take g=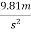
Solution:- Given
r=0.5m

g=
We know
 for avoid skidding
for avoid skidding

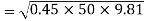
=14.85m/s=53.48 km/hr
Example 8:- A motorcyclist riding at 20km/HR has to turn a corner. Find least radius of curve he should follow for safe travelling. If coefficient of friction between tires and road is 0.2
Solution:- Given
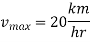
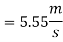
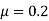
We know
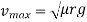
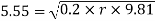
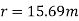
Reference Books
1.Engineering Mechanics by S. S. Bhavikattis, New Age International Pvt. Ltd.
2.Engineering Mechanics by R. K. Bansal and Sanjay Bansal.
3.Vector Mechanics for Engineers Vol.I and II by F. P. Beer and E. R. Johnston, Tata Mc-Graw Hill Publication.
4.Engineering Mechanics by Manoj K Harbola, Cengage Learning
5.Engineering Mechanics by K. I. Kumar, Tata Mc-Graw Hill Publication
6.Engineering Mechanics by S. B. Junnerkar.
7.Engineering Mechanics by Irving H. Shames, Prentice Hall of India, New Delhi.
8.Applied Mechanics by S. N. Saluja, Satya Prakashan, New Delhi.
9.Engineering Mechanics by Statics and Dynamics by Ferdinand Singer, Harper and Row Publications
10.Engineering Mechanics by R. S. Khurmi, S. Chand Publications
11.Fundamentals of Engineering Mechanics by S. Rajasekaran, G. Sankarasubramanian,VikasPublishing House
12) “Applied Mechanics- Dynamics &Statics ” by I.B.Prasad, Khanna Publisher, Delhi