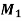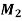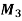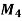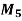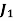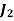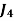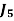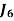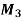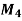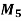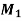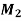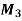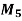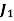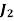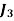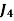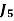Assignment Problem
The assignment problem consists of finding, in a weighted bipartite graph, a matching of a given size, in which the sum of weights of the edges is a minimum. If the numbers a of agents and tasks are equal, then the problem is called balanced assignment. Otherwise, it is called unbalanced assignment.
Example 1:
1 2 3 4 (Tasks)
Column Reduction
A | 19 | 27 | 18 | 12 |
B | 14 | 29 | 30 | 27 |
C | 39 | 20 | 19 | 16 |
D | 20 | 27 | 25 | 11 |
Workers
Solution:
Row reduction:
19-12 | 27-12 | 18-12 | 12-12 |
14-14 | 29-14 | 30-14 | 27-14 |
39-16 | 20-16 | 19-16 | 16-16 |
20-11 | 27-11 | 25-11 | 11-11 |
column reduction:
7 | 15 | 6 | 0 |
0 | 15 | 16 | 13 |
23 | 4 | 3 | 0 |
9 | 16 | 14 | 0 |
7 | 11-3 | 3-3 | 0 |
0 | 11-3 | 13-3 | 13 |
23+3 | 0 | 0 | 0+3 |
9 | 12-3 | 11-3 | 0 |
7-0 | 15-4 | 6-3 | 0-0 |
0-0 | 15-4 | 16-3 | 13-0 |
23-0 | 4-4 | 3-3 | 0-0 |
9-0 | 16-4 | 14-3 | 0-0 |
7 | 11 | 3 | 0 |
0 | 11 | 13 | 13 |
23 | 0 | 0 | 0 |
9 | 12 | 11 | 0 |
|
|
|
|
| 8 | 10 | 13 |
| 0 | 0 | 3 |
| 9 | 8 | 0 |
workers | tasks | hours |
A | 3 | 18 |
B | 2 | 14 |
C | 1 | 20 |
D | 4 | 11 |
Total |
| 63 |
Example 2: Three men are to be given 3 jobs and it is assumed that a person is fully capable of doing job independently. The following table gives an idea of that cost incurred to complete each job by each person
men |
|
|
| supply |
| 20 15 8
| 28 35 32 | 21 17 20 | 1 1 1 |
Demand | 1 | 1 | 1 |
|
Formulate as linear programming problem
Solution: The given problem can easily be formulated as a linear programming(transportation) model as under.
Z = (20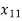 +28
+28 + 21
+ 21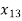 ) + (15
) + (15 +35
+35 + 17
+ 17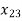 )+ (18
)+ (18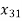 +32
+32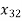 + 20
+ 20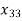 )
)
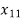 +
+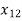 +
+ 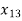 = 1
= 1
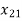 +
+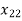 +
+ 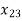 = 1
= 1 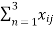 , where i =1, 2, 3, ……
, where i =1, 2, 3, ……
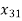 +
+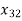 +
+ 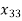 = 1
= 1
Since each job can be assigned to only one person, therefore three equations for three different persons three different jobs.
The given problem is just a special case of the transportation problem.
Balanced problem: A balanced assignment problem means the no. of rows and no. of columns in the problem are equal. E.g. if the problem contains 4 workers and 4 jobs, then it is balanced. Whereas, an unbalanced problem means the no. of rows and no. of columns are not equal. E.g. if the problem contains 4 workers and 3 jobs it is not balanced.
Unbalanced assignment problem: Whenever the cost, Matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix. The dummy rows or columns will contain all cost elements as zeroes. The Hungarian menthod may be used to solve this problem.
The following algorithm applies to Hungarian method.
Step 1: Subtract the smallest entry in each row from all the entries of its row
Step 2: Subtract the smallest entry in each column from all the entries of its column.
Step 3: Draw lines through appropriate rows and columns so the zero entries of the cost matrix are covered and the minimum number of such lines is used.
Step 4: Test for opportunity (i) If the minimum number of covering lines is n, an optimal assignment of zeros is possible and we are finished.
(ii) If the minimum number of covering lines is less than n, an optimal assignment of zeros is not yet possible. In this case, proceed to step 5.
Step 5: Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
From | Denver | Edmonton | Fargo |
Austin | 250 | 400 | 350 |
Boston | 400 | 600 | 350 |
Chicago | 200 | 400 | 250 |
Where should you send each of your salespeople in order to minimize airfare?
Solution:
Step 1: Subtract 250 from row 1, 350 from row2, and 200 from row 3.
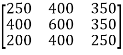

Step 2: Subtract 0 from column 1, 150 from column 2, and 0 from column 3.
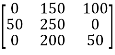
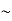
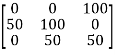


 Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.
Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.
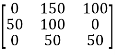
Step 4: Since the minimal number of lines is 3, an optimal assignment of zeros is possible and we are finished. Since the total cost for this assignment is 0, it must be an optimal assignment.
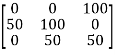
Here is the same assignment made to the original cost matrix.
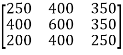
Example 2: A construction company has four large bulldozers located at four different garages. The bulldozers are to be moved to four different construction sites are given below.
Bulldozer site | A | B | C | D |
1 | 90 | 75 | 75 | 80 |
2 | 35 | 85 | 55 | 65 |
3 | 125 | 95 | 90 | 105 |
4 | 45 | 110 | 95 | 115 |
How should bulldozers be moved to the construction sites in order to minimize the total distance travelled?
Solution:
Step 1: Subtract 75 from row 1, 35 from row 2, 90 from row 3, and 45 from row 4.
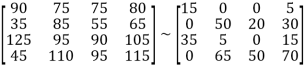
Step 2: Subtract 0 from colum 1, 0 from column 2, 0 from column 3, and 5 from column 4.

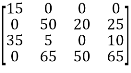


 Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.
Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.
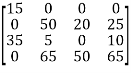
Step 4: Since the minimal number of lines is less than 4, we have to proceed to step 5.
Step 5: Note that 5 is the smallest entry not covered by any line. Subtract from each uncovered row.
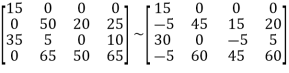
Now add 5 to each covered column.
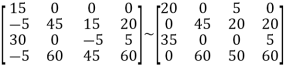
Now return to step 3.
Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.
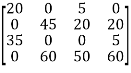


 step 4: Since the minimal number of lines is less than 4, we have to return to step 5.
step 4: Since the minimal number of lines is less than 4, we have to return to step 5.
Step 5: Note that 20 is the smallest entry not covered by a line. Subtract 20 from each uncovered row.
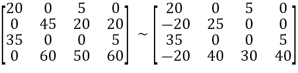
Then add 20 to each covered column.
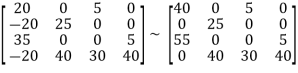
Now return to step 3



 Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.
Step 3: Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines.

Step 4: Since the minimal number of lines is 4, an optimal assignment of zeros is possible and we are finished.

Since the total cost for assignment is 0, it must be an optimal assignment.
Here is the same assignment made to the original cost matrix.
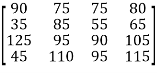
So, we should send Bulldozer 1 to site D, Bulldozer 2 to site C, Bulldozer 3 to site B, and Bulldozer 4 to site A.
Example 1: Using the following cost matrix, determine
(i) Optimal job assignment.
(ii) The cost of assignment.
| A | B | C | D |
1 | 2 | 10 | 9 | 7 |
2 | 15 | 4 | 14 | 8 |
3 | 13 | 14 | 16 | 11 |
4 | 4 | 15 | 13 | 9 |
Solution: Here, no.of rows = no.of columns, In other words, no.of workers = no.of jobs. So, it is a balanced assignment problem.
Step 1: Subtract the smallest element of each row from all the elements of that row.
2 | 10 | 9 | 7 |
15 | 4 | 14 | 8 |
13 | 14 | 16 | 11 |
4 | 15 | 13 | 9 |
0 | 8 | 7 | 5 |
11 | 0 | 10 | 4 |
2 | 3 | 5 | 0 |
0 | 11 | 9 | 5 |
step 2: Subtract the smallest element of each column from all the elements of that column.
0 | 8 | 7 | 5 |
11 | 0 | 10 | 4 |
2 | 3 | 5 | 0 |
0 | 11 | 9 | 5 |
0 | 8 | 2 | 5 |
11 | 0 | 5 | 4 |
2 | 3 | 0 | 0 |
0 | 11 | 4 | 5 |
Step 3: cover all zeros
(a) Cover all zeros of the matrix with the minimum number of horizontal or vertical lines. If the number of lines drawn is equal to the order of the matrix then the solution is optimal.
| 8 | 2 | 5 |
11 | 0 | 5 | 4 |
| 3 | 0 | 0 |
| 11 | 4 | 5 |
The minimum number of lines that cover all the zeros = 3. And is not equal to the number of rows/columns. Proceed to next step.
(b) Select all smallest elements from the matrix which is not covered by lines (here 2 is the smallest and uncovered elements
Subtract the elements from all the uncovered elements and add this smallest element to the element lying at the intersection of lines repeat step 3(a) and 3(b)
As the minimum number of lines that cover all zeros =4. And equal to the number of rows/columns.
Therefore, the solution is optimal.
|
| 2 | 5 |
11 | 0 | 5 | 4 |
| 3 | 0 | 0 |
| 11 | 4 | 5 |
|
|
| 3 |
11 | 0 | 3 | 2 |
| 5 | 0 | 0 |
0 | 11 | 2 | 3 |
Step 4: Assign the zeros.
(a) Examine the rows which contain only one ‘zero ‘element. Make an assignment to this single zero by encircling it. Cross all other zeros, as these will not be considered for any future assignment. Continue till all the rows have been examined.
(b) Now, examine the columns containing only one ‘zero’. Encircle this zero and make an assignment there. Then cross any other zero and continue till all the columns are eliminated
(c) Repeat the step 4(A) and 4(b) until all the assignments have been made.
(d) While assigning, if there is no single zero exists in the row or column, then select any zero arbitrary and encircle it and cross all other zeros in the column and row in respect of which the assignment is made.
Therefore, the optimal job assignment is (1-c), (2-B), (3-D), (4-A)
Total cost = 9+4+11+4 = 28.
Example 2: solve the balanced assignment problem.
jobs persons | 1 | 2 | 3 | 4 |
A | 10 | 12 | 19 | 11 |
B | 5 | 10 | 7 | 8 |
C | 12 | 14 | 13 | 11 |
D | 8 | 12 | 11 | 9 |
Solution: Step 1: row reduction step 2: column reduction
0 | 2 | 9 | 1 |
0 | 5 | 2 | 3 |
1 | 3 | 2 | 0 |
0 | 4 | 3 | 1 |
0 | 0 | 7 | 1 |
0 | 3 | 0 | 3 |
1 | 1 | 0 | 0 |
0 | 2 | 1 | 1 |
person | job | total |
A | 2 | 12 |
B | 3 | 7 |
C | 4 | 11 |
D | 1 | 8 |
Therefore, the optimum cost is Rs.38 (12+7+11+8 =38).
jobs machines |
|
|
|
|
|
| 300 | 290 | 280 | 290 | 210 |
| 250 | 310 | 290 | 300 | 200 |
| 180 | 190 | 300 | 190 | 180 |
| 320 | 180 | 190 | 240 | 170 |
| 270 | 210 | 190 | 250 | 160 |
| 190 | 200 | 220 | 190 | 140 |
| 220 | 300 | 230 | 180 | 160 |
| 260 | 190 | 260 | 210 | 180 |
Solution: first sub-problem:
jobs machines |
|
|
|
|
|
| 180 | 190 | 300 | 190 | 180 |
| 320 | 180 | 190 | 240 | 170 |
| 270 | 210 | 190 | 250 | 160 |
| 190 | 200 | 220 | 190 | 140 |
| 220 | 300 | 230 | 180 | 160 |
870 + 680 = 1550. It can easily be checked using the Hungarian method, that these sub-problems were solved optimally. In their paper,
Yadaiah and Haragopal have a minor typo.
We will now solve the original problem of assigning these eight jobs to five machines such that machine is used at least once, but not more than twice.
Second sub-problem
jobs |
|
|
|
| 290 | 290 | 210 |
| 310 | 300 | 200 |
| 190 | 210 | 180 |
Final Hungarian method cost matrix
|
|
|
|
|
|
|
|
|
|
|
| 40 | 30 | 20 | 30 | 0 | 40 | 30 | 20 | 30 | 0 |
| 0 | 60 | 40 | 50 | 0 | 0 | 60 | 40 | 50 | 0 |
| 0 | 10 | 120 | 10 | 50 | 0 | 10 | 120 | 10 | 50 |
| 140 | 0 | 10 | 60 | 40 | 140 | 0 | 10 | 60 | 40 |
| 80 | 20 | 0 | 60 | 20 | 80 | 20 | 0 | 60 | 20 |
| 0 | 10 | 30 | 0 | 0 | 0 | 10 | 30 | 0 | 0 |
| 40 | 120 | 50 | 0 | 30 | 40 | 120 | 50 | 0 | 30 |
| 70 | 0 | 70 | 20 | 40 | 70 | 0 | 70 | 20 | 40 |
DUM 1 | 0 | 0 | 0 | 0 | 50 | 0 | 0 | 0 | 0 | 50 |
DUM 2 | 0 | 0 | 0 | 0 | 50 | 0 | 0 | 0 | 0 | 50 |
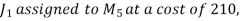
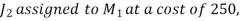
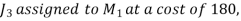

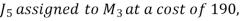
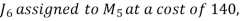
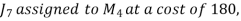
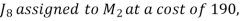
For a total minimum cost of 1520 (not 1550).
Example 2: Let us consider a problem with 8worker and 4 tasks. Its worker-task assignment cost matrix is shown in table
i/j | 1 | 2 | 3 | 4 |
A | 53 | 62 | 42 | 89 |
B | 18 | 35 | 9 | 55 |
C | 93 | 80 | 91 | 83 |
D | 79 | 23 | 96 | 56 |
E | 43 | 16 | 12 | 23 |
F | 43 | 16 | 12 | 20 |
G | 35 | 79 | 25 | 59 |
H | 27 | 16 | 12 | 20 |
Solution:
Step 1: Create an unbalanced matrix problem for worker task assignment cost matrix.
Step 2: Obtain table 2 by adding duplicate or one dummy task with all 1 assignment cost to given table
i/j | 1 | 2 | 3 | 4 | 5 |
A | 53 | 62 | 42 | 89 | 1 |
B | 18 | 35 | 9 | 55 | 1 |
C | 93 | 80 | 91 | 83 | 1 |
D | 79 | 23 | 96 | 56 | 1 |
E | 43 | 16 | 12 | 23 | 1 |
F | 43 | 16 | 12 | 20 | 1 |
G | 35 | 79 | 25 | 59 | 1 |
H | 27 | 16 | 12 | 20 | 1 |
Step 3: Calculate a reduced cost matrix by dividing each row by minimum cost of its column. Reduced cost matrix obtained from table 2.
i/j | 1 | 2 | 3 | 4 | 5 |
A | 2.94 | 3.87 | 3.5 | 4.45 | 1 |
B | 1 | 2.18 | 3.25 | 2.75 | 1 |
C | 5.16 | 5 | 7.58 | 4.15 | 1 |
D | 4.38 | 1.43 | 8 | 2.8 | 1 |
E | 2.38 | 1 | 1 | 1 | 1 |
F | 4.83 | 4037 | 7.25 | 1.55 | 1 |
G | 1.94 | 4.93 | 2.083 | 2.95 | 1 |
H | 1.5 | 1 | 1 | 1 | 1 |
Step 4: Look for the row with one reduced cost excluding 1 from dummy column. Assign worker to task according to position of the choosen 1 and mark entire row to avoid later redundant assignment as shown in above table.
i/j | 1 | 2 | 3 | 4 | 5 |
A | 2.94 | 3.87 | 3.5 | 4.45 | 1 |
B |
| 2.18 | 3.25 | 2.75 | 1 |
C | 5.16 | 5 | 7.58 | 4.15 | 1 |
D | 4.38 | 1.43 | 8 | 2.8 | 1 |
E | 2.38 | 1 | 1 | 1 | 1 |
F | 4.83 | 4037 | 7.25 | 1.55 | 1 |
G | 1.94 | 4.93 | 2.083 | 2.95 | 1 |
H | 1.5 | 1 | 1 | 1 | 1 |
Step 5: Look for the column with one reduced cost excluding 1 from dummy row. Assign worker to task according to position of the chosen 1 and mark entire column to avoid later redundant assignment as shown in above table.
Step 6: Choose one of remaining 1 in the reduced cost matrix as a position to assign worker to task. Mark row and colum of chosen 1 to avoid later redundant assignment. After applying step 6 to the matrix in table 4, we get the new matrix as shown in table 5.
i/j | 1 | 2 | 3 | 4 | 5 |
A | 2.94 |
| 3.5 | 4.45 | 1 |
B |
| 2.18 | 3.25 | 2.75 | 1 |
C | 5.16 | 5 | 7.58 | 4.15 | 1 |
D | 4.38 | 1.43 | 8 | 2.8 | 1 |
E |
| 1 | 1 | 1 | 1 |
F | 4.83 | 4037 | 7.25 | 1.55 | 1 |
G | 1.94 | 4.93 | 2.083 | 2.95 | 1 |
H |
| 1 | 1 | 1 | 1 |
Step 7: Assign dummy task to the first n-m agent from table 5, we assign dummy task to 8-4 workers as shown in table 6x
i/j | 1 | 2 | 3 | 4 | 5 |
A | 2.94 |
| 3.5 | 4.45 | 1 |
B |
| 2.18 | 3.25 | 2.75 | 1 |
C | 5.16 | 5 | 7.58 | 4.15 | 1 |
D | 4.38 | 1.43 | 8 | 2.8 | 1 |
E |
| 1 | 1 | 1 | 1 |
F | 4.83 | 4037 | 7.25 | 1.55 | 1 |
G | 1.94 | 4.93 | 2.083 | 2.95 | 1 |
H |
| 1 | 1 | 1 | 1 |
Step 8: Count the number of assigned text excluding dummy task. If it is equal to the number of tasks then go to step 11(5)
Step 9: Mark row assignment excluding dummy task assignment and mark dummy column. The marked rows/column from our examples are shown in table 7.
i/j | 1 | 2 | 3 | 4 | 5 |
A | 2.94 |
| 3.5 | 4.45 |
|
B |
| 2.18 | 3.25 | 2.75 | 1 |
C | 5.16 | 5 | 7.58 | 4.15 | 1 |
D | 4.38 | 1.43 | 8 | 2.8 | 1 |
E |
| 1 | 1 | 1 | 1 |
F | 4.83 | 4037 | 7.25 | 1.55 | 1 |
G | 1.94 | 4.93 | 2.083 | 2.95 | 1 |
H |
| 1 | 1 | 1 | 1 |
Step 10: Look for the minimum cost among remaining (unmarked) costs. Recalculate the reduced cost table by dividing each remaining cost by the minimum cost and replace 0 at intersection with the minimum cost. And go to step 4. Table 8 shows the modified reduced matrix.
i/j | 1 | 2 | 3 | 4 | 5 |
A | 1.51 | 2.44 | 2.07 | 3.02 | 1 |
B | 1 | 2.18 | 3.25 | 2.75 | 1.43 |
C | 3.73 | 3.57 | 6.15 | 2.72 | 1 |
D | 2.95 | 0 | 6.57 | 1.37 | 1 |
E | 2.38 | 1 | 1 | 1 | 1.43 |
F | 3.4 | 2.94 | 5.82 | 0.12 | 1 |
G | 0.51 | 3.5 | 0.65 | 1.52 | 1 |
H | 1.5 | 1 | 1 | 1 | 1.43 |
Step 11: Calculate total assignment cost.
Suppose B - >1, D - >2, E – >3 and H - >4. The total cost for this assignment is calculated as follows.
Min(T) = 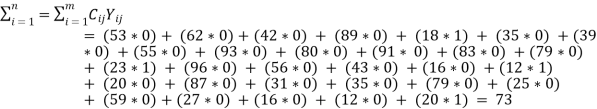
Step 1: solve the problem as assignment problem
Step 2: check for complete cycle or alternative cycles. If the cycle is complete, go to step 4. If not, go to the step 3.
Step 3: to start with, assign the next least element other than zero, (only for first allocation) and complete the assignment. Go to step 2.
Step 4: write the optimum assignment schedule and calculate the cost/time.
Example 1: A travelling salesman has to visit five cities. He wishes to start from a particular city, visit each city and then return to his starting point. The travelling cost (in Rs.) of each city from a particular city is given below.
Travelling salesman problem:
From city To city | A | B | C | D | E |
A | A | 2 | 5 | 7 | 1 |
B | 6 | a | 3 | 8 | 2 |
C | 8 | 7 | a | 4 | 7 |
D | 12 | 4 | 6 | a | 5 |
E | 1 | 3 | 2 | 8 | a |
What should be the sequence of the salesman’s visit, so that the cost is minimum?
Solution: The optimal solution is reached using Hungarian method.
From city To city | A | B | C | D | E |
A | A | 1 | 3 | 6 | 0 |
B | 4 | a | 0 | 6 | 0 |
C | 4 | 3 | a | 0 | 3 |
D | 8 | 0 | 1 | a | 1 |
E | 0 | 2 | 0 | 7 | a |
The assignment shown in the above table gives the route sequence
A B, B
B, B C, C
C, C D, D
D, D E, E
E, E A
A
The travelling cost to this solution is 2000 + 3000 + 4000 + 5000 + 1000 = 15,000.
Therefore, the sequence feasible for this assignment is
A with the travelling cost of Rs. 15,000.
with the travelling cost of Rs. 15,000.
Example 2: A sales man has to visit five cities A, B, C, D AND E.the intercity distances are tabulated below
To/from | A | B | C | D | E |
A | - | 12 | 25 | 26 | 16 |
B | 7 | - | 17 | 19 | 8 |
C | 10 | 11 | - | 19 | 12 |
D | 15 | 18 | 23 | - | 17 |
E | 12 | 14 | 24 | 26 | - |
The above distances in km between two cities need not be same both ways. Which route would you advise the salesman to take so that the total distance travelled by him is minimum, if the salesman starts from city A and has to come back to city ‘A’.
Solution: step 1: Select smallest element in each row and subtract it from every element of that row. Row reduction results in the following table.
To/from | A | B | C | D | E |
A | - | 0 | 13 | 14 | 4 |
B | 0 | - | 10 | 12 | 1 |
C | 0 | 1 | - | 9 | 2 |
D | 0 | 3 | 8 | - | 2 |
E | 0 | 2 | 12 | 14 | - |
Step 2: Select the minimum element in each column and subtract this element from every element in that column, we get
To/from | A | B | C | D | E |
A | - | 0 | 5 | 5 | 3 |
B | 0 | - | 2 | 3 | 0 |
C | 0 | 1 | - | 0 | 1 |
D | 0 | 3 | 0 | - | 1 |
E | 0 | 2 | 4 | 5 | - |
Step 3: Cover all zeros and get the final minimum solution
To/from | A | B | C | D | E |
A | - | 0 | 5 | 5 | 3 |
B | 0 | - | 2 | 3 | 0 |
C | 0 | 1 | - | 0 | 1 |
D | 0 | 3 | 0 | - | 1 |
E | 0 | 2 | 4 | 5 | - |
Optimal schedule is B  C, C
C, C  D, D
D, D  E, E
E, E  A
A
Involving distance 12 + 17 + 19 + 12 = 77 km.
This route satisfies the travelling salesman problem.
Reference