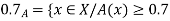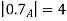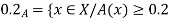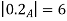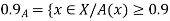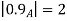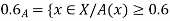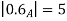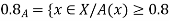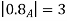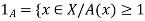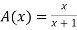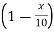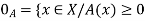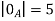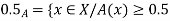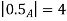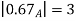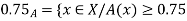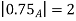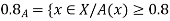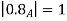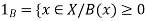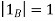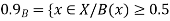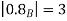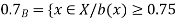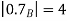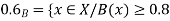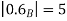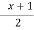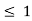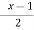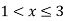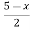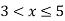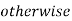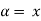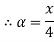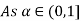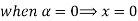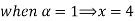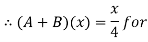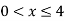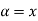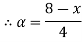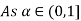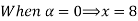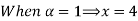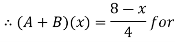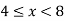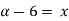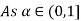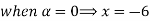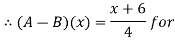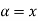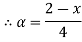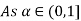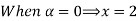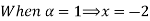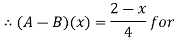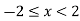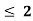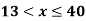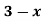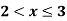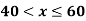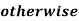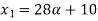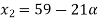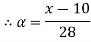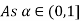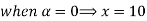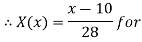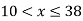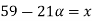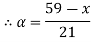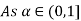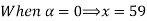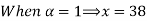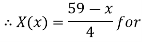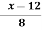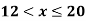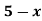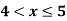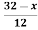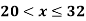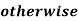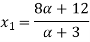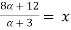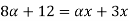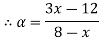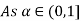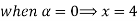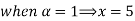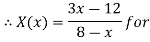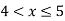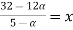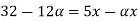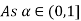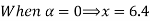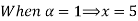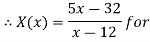Unit – 5
Fuzzy Arithmetic
A fuzzy number is a generalization of a regular, real number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function.
1. Set A must be normal Fuzzy set;
2. 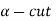 of A must be closed interval foe every
of A must be closed interval foe every 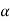 in (0,1]
in (0,1]
3. Support and strong  of A must be bounded.
of A must be bounded.
Example 1: It is necessary to compare 2 sensors based upon their detection levels & gain settings the tails of gain settings & sensor detection level with a obtained item being monitored providing typical membership values to reprocess the detection levels for each sensor is given in tales.
Find following membership function:
a)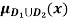 b)
b) 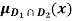 c)
c)
Solution:
Gain setting | Detection level of sensor 1(D1) | Detection level sensor 2(D2) |
0 | 0 | 0 |
10 | 0.2 | 0.35 |
20 | 0.35 | 0.25 |
30 | 0.65 | 0.8 |
40 | 0.85 | 0.95 |
50 | 1 | 1 |


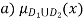 = max {
= max {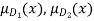 }
}
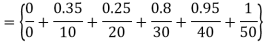
b) 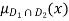 = min {
= min {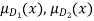 }
}
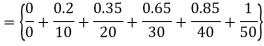
c) 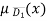 = 1-
= 1-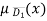
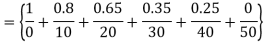
Definition: If aA is a fuzzy set defined on universal set X then its fuzzy cardinality is denoted and defined as 
Where  is membership grade from given fuzzy set A and
is membership grade from given fuzzy set A and  is a scalar cardinality (total number of elements present in crisp set) of corresponding
is a scalar cardinality (total number of elements present in crisp set) of corresponding 
Example 1: Find the fuzzy cardinality of A defined as follows:
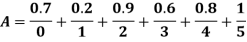
Solution: Here X= {0,1,2,3,4,5} 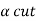 s and its scalar cardinality are
s and its scalar cardinality are
| {0,2,4,5} |
|
| {0,1,2,3,4,5} |
|
| {2,5} |
|
| {0,2,3,4,5} |
|
| {2,4,5} |
|
| {5} |
|
Thus,

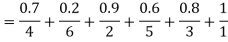
Note: Fuzzy cardinality of Fuzzy set is a fuzzy set
Example 2: Find fuzzy cardinality of fuzzy set A and B whose membership function are given as follows 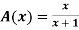 , B(x)=
, B(x)=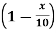 where x
where x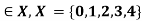
Solution:
X | 0 | 1 | 2 | 3 | 4 |
| 0 | 0.5 | 0.67 | 0.75 | 0.8 |
B(x)= | 1 | 0.9 | 0.8 | 0.7 | 0.6 |

| {0,1,2,3,4} |
|
| {1,2,3,4} |
|
| {2,3,4} |
|
| {3,4} |
|
| {4} |
|
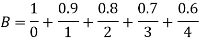
| {0} |
|
| {0,1} |
|
| {0,1,2} |
|
| {0,1,2,3} |
|
| {0,1,2,3,4} |
|
Thus,
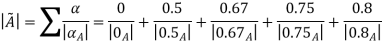
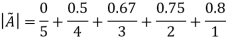
Thus,
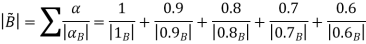

Moving from intervals we can define arithmetic on fuzzy numbers based on principles of interval Arithmetic.
Let A and B denote fuzzy numbers and let * denote any of the four basic arithmetic operations. Then, we define a fuzzy set on R, A*B by defining its alpha-cut as:
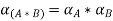
Arithmetic Operations on Intervals: Arithmetic operations on fuzzy intervals satisfy following useful properties:
Properties:
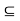
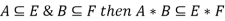
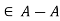
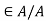
Examples Illustrating interval-valued arithmetic operations:
Applying the extension principle to arithmetic operations, we have
Fuzzy Addition: 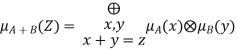
Fuzzy Subtraction 
Fuzzy Multiplication 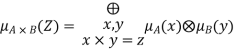
Fuzzy Division 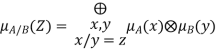
Example 1:
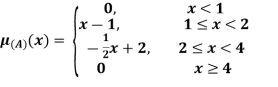
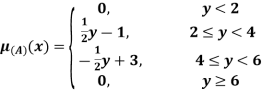
Their 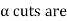

Step 1: Find 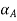 and
and 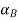
Step 2: Use decomposition theorem which is given as 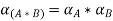 and arithmetic operation on closed interval
and arithmetic operation on closed interval
Step 3: Find membership function.
Example 2: The membership function of two fuzzy numbers A and B are given as follows
A(x) | = | -1 < x |
B(x) | = |
|
= |
| = |
| ||
= 0 |
| = 0 | otherwise |
Find A+B and A-B
Solution:
Step 1: Find 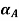 and
and 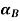
For -1 < x 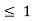
By def. of  ,
,
A(x)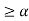
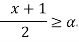
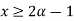
For 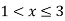
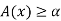
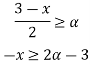
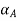 = [2
= [2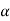 -1, 3-2
-1, 3-2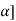 for all
for all 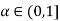
For 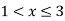
By def. of 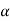 cut,
cut,
B(x)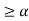

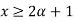
For 3 < x 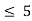
B(x)
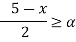
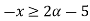
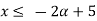
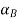 = [2
= [2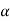 +1, 5-2
+1, 5-2 for all
for all 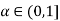
Step 2: By decomposition theorem & arithmetic operation on closed interval we find 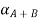 as follows.
as follows.
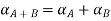
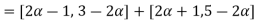

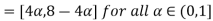
Step 3: Now find membership function
Let 4
| Let 8-4
|
Thus, (A+B) (x) =  ; 0 < x
; 0 < x 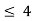
= 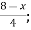 4
4
= 0; Otherwise
To find A-B
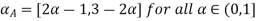
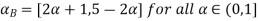
Step 4: By decomposition theorem and arithmetic operation on closed interval we find 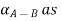 follows
follows
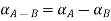
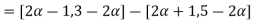
= [
= [4 for all
for all
Step 5: Now find membership function to define fuzzy numbers A-B
Let 4
| Let 2-4
|
Thus,
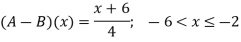

Algorithm:
Step 1: Find 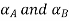
Step 2: Use decomposition theorem which is given as 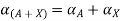
Let
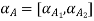

A+X = B
Taking alpha cut on both side
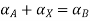
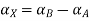
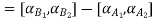
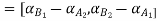

Step 3: Find membership function
Example 1: The membership function of two fuzzy numbers A and B are
A(x) | = x-1 | 1 < x |
B(x) | = |
|
= |
| = |
| ||
= 0 |
| = 0 | otherwise |
Solve A+X =B
Solution: 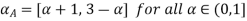
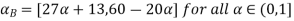
Let 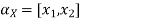
A+X = B
Taking alpha cut on both side
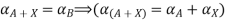
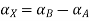
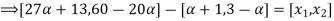
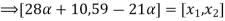
Check 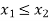
|
|
|
0.1 | 12.8 | 56.9 |
0.6 | 26.8 | 46.4 |
0.8 | 32.4 | 42.2 |
Thus, 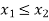 hence solution exists.
hence solution exists.
Let
| Let
|
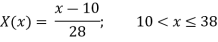
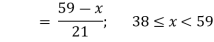
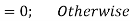
Example 2: The membership function of two fuzzy numbers A and B are
A(x) | = x-3 | 3 < x |
B(x) | = |
|
= |
| = |
| ||
= 0 |
| = 0 | otherwise |
Solve A.X =B
Solution: 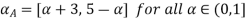
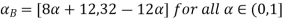
Let 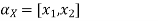
A.X = B
Taking alpha cut on both side
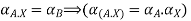
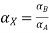
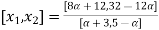
Check 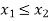
|
|
|
0.3 | 4.3636 | 6.0426 |
0.7 | 4.7568 | 5.4884 |
0.9 | 4.9231 | 5.1707 |
Thus, 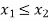 hence solution exists.
hence solution exists.
Let
| Let
|
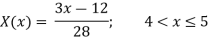
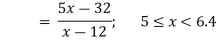
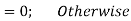
Reference