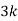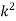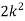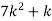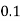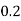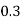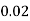Unit – 2
Probability Distribution
Definition of Random Variable: A random variable is a variable whose possible values are the numerical outcomes of a random experiment. Therefore, it is a function which associate a unique numerical value with every outcome of an experiment. Further, its value varies with every trial of the experiment.
Random Variables:
continuous random variable: A continuous random variable is a random variable where the data can take infinitely many values. For example, a random variable measuring the time taken for something to be done is continuous since there are an infinite number of possible times that can be taken.
Continuous random variable is called by a probability density function p (x), with given properties: p (x) ≥ 0 and the area between the x-axis& the curve is 1: ... standard deviation of a variable Random is defined by σ x = √Variance (x).
Properties
Starting from properties 1 to 7, c is a constant; x and y are random variables.
From given properties 8 to 12, w and v is random vector; b is a continuous vector; A is a continuous matrix.
8. E(v + w) = E(v) + E(w)
9. E(b) = b
10. E(Av) = A E(v)
11. Co-variance(v + b) = Co-variance(v)
12. Co-variance (Av) = A Co-variance(v) AT
Example 1: Consider tossing a fair coin 3 times.
Define X= the number of heads obtained.
Value | 0 | 1 | 2 | 3 |
Probability | 1/8 | 3/8 | 3/8 | 1/8 |
A: what is the probability of tossing at least two heads?
B: what is the probability of tossing fewer than three heads?
Solution:
X = 0, TTT
X = 1, HTT THT TTH
X = 2, HHT HTH THH
X = 3, HHH
A: Ans: 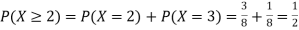
B: Ans: 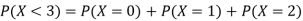
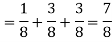
(Or) 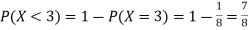
Example 2: Let the random variable X have probability density function

Find the cumulative distribution function of Y = g(x) = 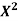
Solution:
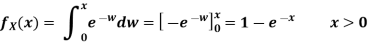
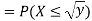
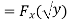
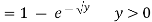
Example 3: Let X be a random variable with PDF given by
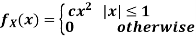
a. Find the constant c
b. Find EX and Var(X)
c. Find P(X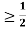 )
)
Solution: a. To find c, We can use 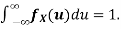

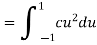
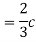
Thus, we must have c=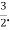
b. To find EX, we can write
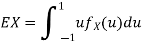

In fact, we could have guessed Ex=0 because the PDF is symmetric around x=0. To find Var(X), We have
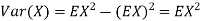
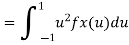
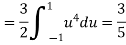
c. To find P(X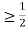 ), we can write
), we can write
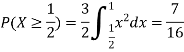
Example 4: Let X be a continuous random variable with PDF given by
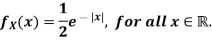
If Y = 
Solution:
First, we note that 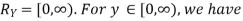
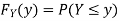
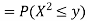
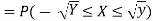


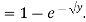
Thus,
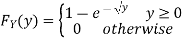
Example 5: Let X be a continuous random variable with PDF
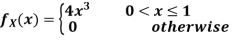
Find P(X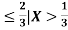 ).
).
Solution: We have
P(X ) =
) = 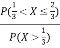
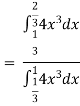
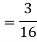
Discrete Probability Distribution:
Example 1: The probability distribution of a discrete random variable X is shown below.
X | 1 | 2 | 3 | 4 | 5 | 6 |
Pr(X=x) | 0.02 | 0.13 | 0.38 | 0.17 | 0.05 | 0.25 |
Find: a) Pr(X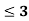 ) b) Pr(X<5) c) Pr(X>0) d) Pr (2
) b) Pr(X<5) c) Pr(X>0) d) Pr (2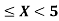 )
)
e) Pr(X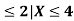 )
)
Solution:
a): Pr(X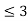 ) = Pr (X=0)+Pr(X=1)+Pr(X=2)+Pr(X=3)
) = Pr (X=0)+Pr(X=1)+Pr(X=2)+Pr(X=3)
= 0.02+0.13+0.38+0.17
= 0.7.
Working with Discrete Probability Distribution:
Example 2:
X | 0 | 1 | 2 | 3 | 4 or more |
P(X) | 0.1 | 0.4 | 0.35 | 0.1 | 0.05 |
a): Verify that this is a legitimate probability distribution.
b): What is the probability that a customer does not rent any videos?
Solution:
a): Confirm that the sum of the probability is 1.
0.1+0.4+0.35+0.1+0.05 = 1
b): This is P(X=0) =0.1 or 10% of customer do not rent any videos.
Please notice the notation.
A probability distribution is a arithmetical function which defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on a number of influences. These factors include the distribution's mean, SD, skewness, and kurtosis.
Example 1: Following probability distribution
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(x) | 0 |
|
|
|
|
|
|
|
Find: (i) k (ii) 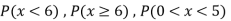
(iii) Distribution function
(iv) If 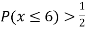 find minimum value of C
find minimum value of C
(v) Find 
Solution:
If P(x) is p.m.f –

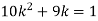
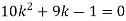
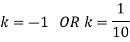
(i)
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(x) | 0 |
|
|
|
|
|
|
|
(ii)
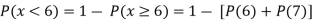
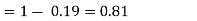
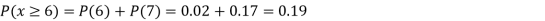
(iii)

(iv)


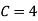
(v)
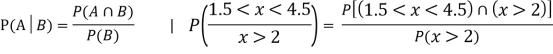
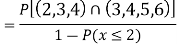
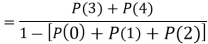
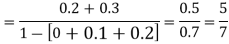
Example 2: There are very few continuous distributions that we can do much with without a lot of math, but the simple uniform distribution is one of them. A uniform distribution is one that is just that-uniform. If we image any possible number between o and 2 as equally likely, we have an infinite possible number of numbers, so the probability of any particular number is close to zero. Instead of focusing on particular numbers, we have to focus on intervals.
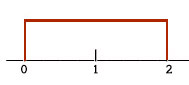
The probability that some number between zero and two will come up will be one. To find the probability of any interval, we find the length of the interval and multiply by 5. Hence, the probability of getting a number between zero and one is 5.
For the following, draw the picture and compute the probabilities. What is:
a): P(0<x<.8)
b): P(x>.8)
c): P(.5<x<1.5)
d): P(.5<x<1.2) or P(.8<x<1.3)
e): compute the probability that we will not be in the interval of .4 to 1.5
f): compute the middle interval in which we will be 90% of the time.
g): compute the tails (outside intervals) that we will be in 5% of the time
Solution:
a): .8*.5 = .40
b): 1-.4 = .6
c): 1*.5 = .5
d): P(.5<x<1.5) = .8*.5 = .4
e): 1-P(.4<x<1.5) = 1-1.1*5 = 1-.55 = .45
f): 90% of 2 is 1.8, which centered will be from .1 to 1.9
g): 95% of the time we will be in the interval .05 to 1.95. 5% of the time we will
between 0 and .05 or 1.95 and 2.
Example 3: The picture below shows a continuous probability distribution with the formula, y = .5x for the range, x =0 to x = 2. In this case, area is probability.
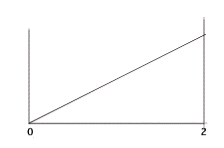
To compute the probability of being between 0 and 1, for example, you need to know y when x equals 1. The formula says it is .5. Hence, to find the probability that x is between 0 and 1 Prob(0<x<1), we compute the area of the triangle with a length of 1 and a height of .5. The answer is 2.5 because .5HW = .5*.5*1.
a). Show that the area under the line is equal to 1.
b). Find the following probabilities:
Prob(0<x<.5)
Prob(0<x<1.5)
Prob(1.5<x<2)
Prob(.5<x<1.5)
Prob (x<.5 or x>1.5)
c). Suppose that we draw twice from this distribution and that probability of the second draw is independent of the first. What is the probability of getting greater than 1.5 on both draws? What is the probability of getting less than 1.5 on both draws? What is the probability of getting a result greater than 1.5 on one draw and less than 1.5 on the other draw?
Solution:
a): Length *height*.5 is the area of a triangle. This triangle has length of 2 and height of 1, so 2*1*.5= 1. The area is one, and for a continuous distribution, area is probability.
b): Prob(0<x<.5)
Prob(0<x<.5) = .5*.5*.25 = .0625
Prob(0<x<1.5) = .5*1.5*.75 = .5625
Prob(1.5<x<2) = 1-Prob(0<x<1.5) = 1-.5625 = .4375.
Prob(.5<x<1.5) = .5625 - .0625 = .5
Prob (x<.5 or x>1.5) = .0625+.4375 = .5
c): Both less than 1.5: .5625*.5625 = .3164: both greater than 1.5: .4375*.4375 = .1914; one greater and one less: 1 - .3164 - .1914 = .4922.
A distribution is said to be binomial distribution if the following conditions are met.
If all the above conditions met then the binomial distribution describes the probability of X successes in n trials.
A classic example of the binomial distribution is the number of heads (X) in n coin tosses.
The Notation for a binomial distribution is
X ~ B (n, π)
which is read as ‘X is distributed binomial with n trials and probability of success in one trial equal to π’.
formula for binomial distribution:
Using this formula, the probability distribution of a binomial random variable X can be calculated if n and π are known.
p(x) = 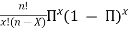
n! is called ‘n factorial’ = n(n-1)(n-2) . . .(1)
P(X) = #of Scenario * Single Scenario
The first factorial terms gives the number of scenario and the second term describes the probability of success to power of number of successes and probability of failure to the power of number of failures.
Binomial Distribution-Mean and Variance:
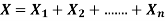


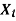
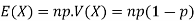
Example 1: Jean usually makes half of her free throws in basketball practice. Today, she tries 3 free throws. What is the probability that Jean will make exactly 1 of her free throws?
Solution: The Probability that Jean will make each free throw is 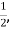 or 0.5.
or 0.5.
P(r) = 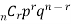 Substitute 3 for n, 1 for r, 0.5 for p, and 0.5 for q
Substitute 3 for n, 1 for r, 0.5 for p, and 0.5 for q
P (1) = 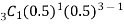
= 3(0.5)(0.25) = 0.375
The probability that Jean will make exactly one free throw is 37.5%.
Example 2: Suppose the probability of purchasing a defective computer is 0.02. What is the probability of purchasing 2 defective computers in a group of 10?
X = 2, n = 10, and 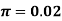
Solution: P(X=2) = 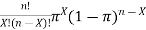
=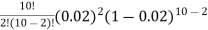
= (45)(0.0004)(0.8508)
= 0.01531
Example 3: A dozen eggs contain 3 defectives. If a sample of 5 is taken with replacement, find the probability that.
a) Exactly 2 of the eggs sampled are defective.
b) 2 or fewer of the eggs sampled are defective
Solution: If n = 5, P = ¼
“Success = Defective”
x = 0,1,2,3,4,5
f(x) = 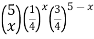
P(X=2) = f(2)= 
P(X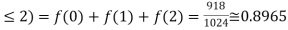
Examples of events over space or time: -number of cells in a specified volume of fluid
-number of calls/hours to a help line
-number of emergency room beds filled/ 24 hours
Like the binomial distribution and the normal distribution, there are many Poisson distributions.
The probability that there are exactly X occurrences in the specified space or time is equal to
p(x) = 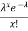
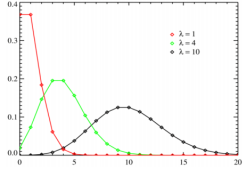
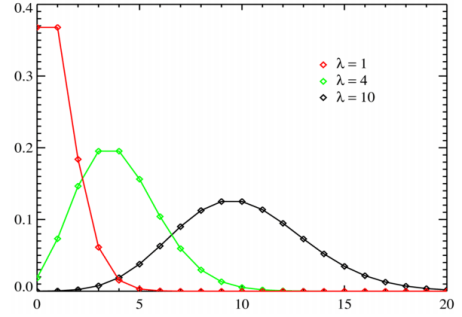
The horizontal axis is the index X. The function is defined only at integer values of X. The connecting lines are only guiding for the eye and do not indicate continuity. Notice that as λ increases the distribution begins to resemble a normal distribution.
Mean and Variance for the Poisson Distribution:
The Mean is: 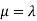
The Variance is: 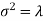
So, the standard deviation is 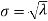 .
.
Example 1: Suppose that a rare disease has an incidence of 1 in 1000 person-years. Assuming that members of the population are affected independently, find the probability of k cases in a population of 10,000(followed over 1 year) for k=0,1,2.
Solution: The expected value (mean) 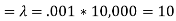
10 new cases expected in this population per year
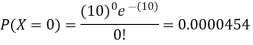
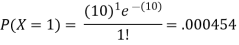
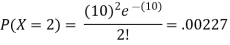
Example 2: Suppose that the probability of a defect in a foot of magnetic tape is 0.002. Use the Poisson distribution to compute the probability that 1500 feet roll will have no defects.
Solution:

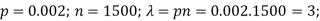
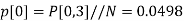
The normal distribution is the utmost broadly identified P.D. then it defines many usual spectacles.
The PDF of the normal distribution is shown by method
f(x)=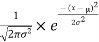 ,
,
where μ is mean of the distribution, and 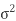 is the variance.
is the variance.
The 2 limitations μ and σ completely describe the figure and all additional things of the normal distribution function.
Properties of normal distribution:
Example 1: The weekly incomes of shit foremen in the glass industry follow the normal probability distribution with a mean of $1,000 and a standard deviation of $ 100. What is the z value for the income, let’s call it X, of a foreman who earns $1,100 per week? For a foreman who earns $900 per week?
Solution: For X = $ 1,100:

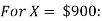
Systolic Blood Pressure:
Example 2: From the Below Diagram find the area of the both sides of the distribution.
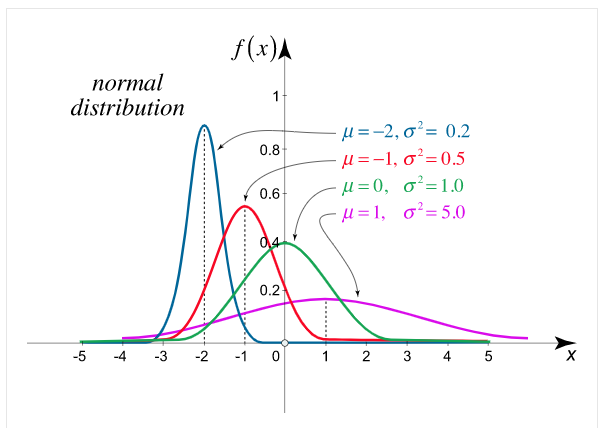
Solution: Area to the left of the positive z: 0.05000+0.3000=0.8000.
Using Table E, z 0.84. X = 120+0.84(8) =126.72
0.84. X = 120+0.84(8) =126.72
Area to the left of the negative z= 0.5000-0.3000=0.2000
Using Table E, z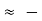 0.84. X = 120-0.84(8) =113.28
0.84. X = 120-0.84(8) =113.28
The middle 60% of readings are between 113 and 127.
Reference