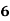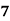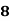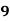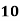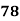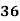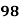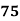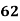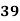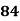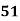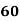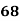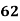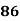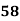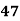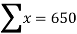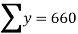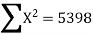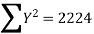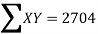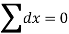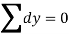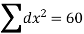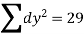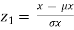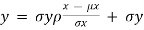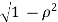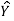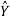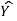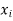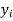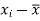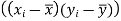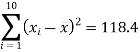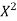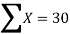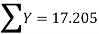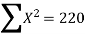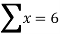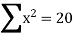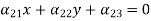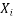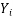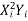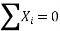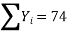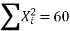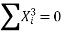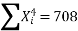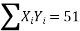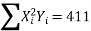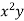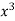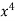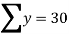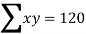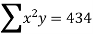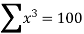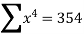Unit – 1
Correlation, Regression & Curve Fitting
Correlation: correlation is statistical measure that indicates the extent to which two or more variables fluctuate in relation to each other. A positive corelation indicates the extent which those variables increase or decrease in parallel; a negative correlation indicates the extent to which one variable increase as the other decreases.
Regression: Regression is a statistical measure used in finance, investing and other disciplines that attempts to determine the strength and character of the relationship between one dependent variable (usually denoted by y) and a series of other variables (known as independent variables).
Curve fitting: Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subjects to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is requires or smoothing, in which a smooth function is constructed approximately fits the data.
Pearson’s Coefficient Correlation: Karl Pearson’s coefficients of correlation an extensive used mathematical method in which the numerical representation is applied to measure the level of relation between linear related variables. The coefficient of correlation is expressed by ‘r’.
Karl Pearson Correlation Coefficient Formula:
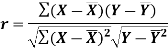
Where, 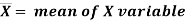
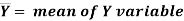
Alternative Formula (Covariance Formula):
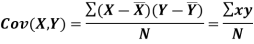
Example 1: Ten students got the following percentage of marks in Economics and Statistics
Calculate the 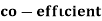 of correlation.
of correlation.
Roll No. |
|
|
|
|
|
|
|
|
|
|
Marks in Economics |
|
|
|
|
|
|
|
|
|
|
Marks in |
|
|
|
|
|
|
|
|
|
|
Solution: Let the marks of two subjects be denoted by 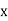 and
and 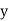 respectively.
respectively.
Then the mean for  marks
marks 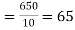 and the mean ofy marks
and the mean ofy marks 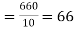
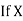 and
and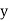 are deviations ofx’s and
are deviations ofx’s and 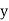 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | Y | X=x-65 | Y=y-66 | X2 | Y2 | XY |
78 36 98 25 75 82 90 62 65 39 | 84 51 91 60 68 62 86 58 53 47 | 13 -29 33 -40 10 17 25 -3 0 -26 | 18 -15 25 -6 2 -4 20 -8 -13 -19 | 169 841 1089 1600 100 289 625 9 0 676 | 324 225 625 36 4 16 400 64 169 361 | 234 435 825 240 20 -68 500 24 0 494
|
|
|
|
|
|
|
|
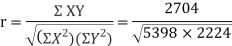
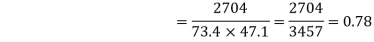
Example 2: Compute coefficient of correlation by Karl Pearson Method for the following data.
X: | 1800 | 1900 | 2000 | 2100 | 2200 | 2300 | 2400 | 2500 | 2600 |
F: | 5 | 5 | 6 | 9 | 7 | 8 | 6 | 8 | 9 |
Solution: Let the A.M.s 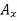 and
and 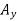 be 2200 and 6 for X and Y series respectively.
be 2200 and 6 for X and Y series respectively.
X | Y | dx | (i=100) dx | dy | d | d | dxdy |
1800 1900 2000 2100 2200 2300 2400 2500 2600 | 5 5 6 9 7 8 6 8 9 | -400 -300 -200 -100 0 100 200 300 400 | -4 -3 -2 -1 0 1 2 3 4 | -1 -1 0 3 1 2 0 2 3 | 16 9 4 1 0 1 4 9 16 | 1 1 0 9 1 4 0 4 9 | 4 3 0 -3 0 2 0 6 12 |
N=9 |
|
|
|
|
|
|
|
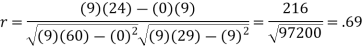
(Note: We can also proceed dividing X by 100)
A bivariate distribution, set only, is the probability that a definite event will happen when there are 2 independent random variables in your scenario. E.g, having two bowls, individually complete with 2dissimilarkinds of candies, and drawing one candy from each bowl gives you 2 independent random variables, the 2dissimilar candies. Since you are pulling one candy from each bowl at the same time, you have a bivariate distribution when calculating your probability of finish up with specific types of candies.
Properties:
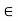
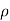
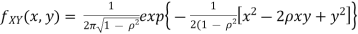 ,
,
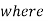
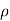
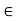 (-1, 1). If
(-1, 1). If 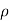 = 0, then we just say X and Y have the standard bivariate normal distribution.
= 0, then we just say X and Y have the standard bivariate normal distribution.
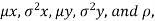
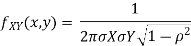
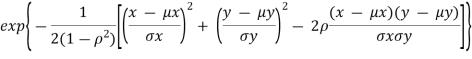
where  are all constants.
are all constants.

E [ y|X =x] = 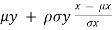 ,
,
Var (Y| X = x) = (1- 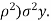
Bivariate Regression:
Where: Y = the line’s position on the vertical axis at any point
X = the line’s position on the horizontal axis at any point.
m = the slope of the line
b = the intercept with the Y axis, where X equals zero
An illustration of Bivariate data:
| 1 | 2 | 3 | Total |
1 | 300 | 0 | 0 | 300 |
2 | 50 | 300 | 50 | 400 |
3 | 0 | 100 | 200 | 300 |
Total | 350 | 400 | 250 | 1000 |
Example 1: Let  random variables. Define
random variables. Define
X = 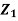
Y = 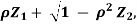 where
where 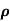 is real number in (-1, 1).
is real number in (-1, 1).
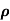
Solution: first, note that since  are normal and independent, they are jointly normal, with the joint PDF.
are normal and independent, they are jointly normal, with the joint PDF.
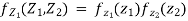
= 
(a). we need to show that aX + bY is normal for all a,b  R, we have
R, we have
aX + bY = 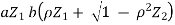
= 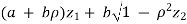
Which is linear combination of  and thus it is normal.
and thus it is normal.
(b). we can use the method of transformations to find the joint PDF of X and Y.
The inverse transformation is given by

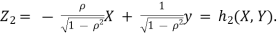
Where J = det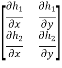 = det
= det 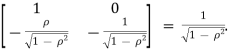
Thus, we conclude that
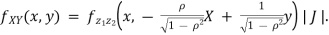
= 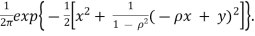

= 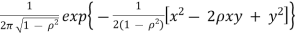
(c). To find  (X, Y), first note that
(X, Y), first note that
Var(X) = Var(Z1) = 1,
Var(Y) = 
Therefore, 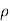 (X, Y) = Cov (X, Y)
(X, Y) = Cov (X, Y)
= Cov( 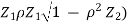
= Cov(
Cov(  .
.
= 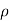 .1 +
.1 + 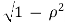 . 0
. 0
= 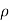 .
.
Example 2: Let X and Y be jointly normal random variables with parameters 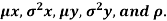 Find the conditional distribution of Y given X =x.
Find the conditional distribution of Y given X =x.
Solution: one way to solve this problem is by using PDF formula. In particular, since X 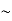 N (
N (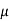 x,
x, 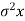 ), we can use
), we can use
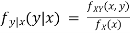 .
.
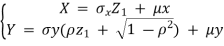
Thus, given X = x we have,
Since 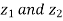 are independent, knowing
are independent, knowing  does not provide any information on
does not provide any information on  . We have shown that given X =x, Y is a linear function of
. We have shown that given X =x, Y is a linear function of 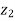 , thus it is normal. In particular
, thus it is normal. In particular
E[Y|X =x ]=  +
+ 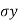
 E
E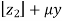
= 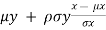 ,
,
Var (Y|X = x) = 
= (1 - 
We conclude that given X = x, Y is normally distributed with mean 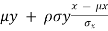 and variance (1 -
and variance (1 - 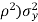 .
.
Example 3: Let X and Y be jointly normal random variables with parameters 
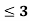
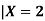
Solution: a. Since X and Y are jointly normal, the random variable V=2X+Y is normal. We have
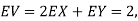
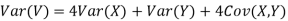
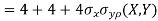
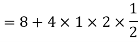
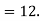
Thus, V 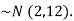 Therefore,
Therefore,
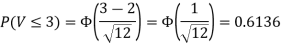
b. Note that Cov (X, Y) = 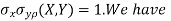
Cov (X+Y, 2X-Y) = 2Cov (X, X)-Cov (X, Y) +2Cov (Y, X)-Cov (Y, Y)
= 2-1+2-4 = -1.
d. Using Properties, we conclude that given X = 2, Y is normally distributed with
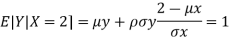
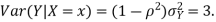
Thus, 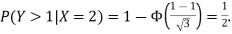
Example 4: Two Way Frequency Tables:
Student Grades in Science Projects.
| Male | Female |
A | 9 | 12 |
B | 18 | 14 |
C | 8 | 11 |
D | 2 | 3 |
F | 1 | 2 |
Solution:
| Male | Female | Total |
A | 9 | 12 | 21 |
B | 18 | 14 | 32 |
C | 8 | 11 | 19 |
D | 2 | 3 | 5 |
F | 1 | 2 | 3 |
Total | 38 | 42 | 80 |
Q: How Many students earned a grade of A?
Ans: 21 Students
Q: How many males were surveyed?
Ans: 38 Male Students
Q: How many males earned a grade of A?
Ans: 9 Male Students
Q: How many students earned a grade of B or C:
Ans: 51 Students
Example 5:
x | 1 2 3 4 5 6 7 |
y | 0.5 2.5 2.0 4.0 3.5 6.0 5.5 |
Solution:
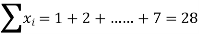
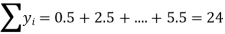
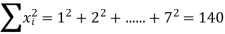

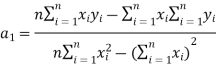
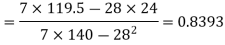
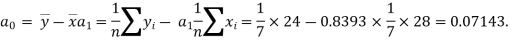
 : y = 0.07143+0.8393x.
: y = 0.07143+0.8393x.
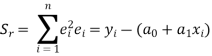
Curve Fitting of Type y = a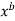 Algorithm
Algorithm
In this article we are going to develop an algorithm for fitting curve of type
y = a using least square regression method.
using least square regression method.
Procedure for fitting y = a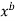
We have,
y = a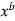 …………. (1)
…………. (1)
Taking log on both side of equation (1), we get
Log(y) = log (a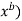
Log(y) = log(a)+log(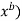
Log(y) = log(a)+b*log(x)------------(2)
Then equation (2) becomes.
Y = A+ bX---------(3)
Now we fit equation (3) using least square regression as:
∑Y = n A+ b ∑X
∑XY = A∑X + b∑X2
2. Solve normal calculations as simultaneous equations for A and b
3. We calculate a from A using: a = exp(A)
4. Substitute the value of a and b in y = a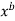 to find line of best fit
to find line of best fit
Fit a least square line for the following data. Also find the trend values and show that ∑(Y–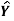 )=0 ∑(Y–
)=0 ∑(Y– )=0.
)=0.
X | 1 | 2 | 3 | 4 | 5 |
Y | 2 | 5 | 3 | 8 | 7 |
Solution:
X | Y | XY | X2 |
| Y– |
1 | 2 | 2 | 1 | 2.4 | -0.4 |
2 | 5 | 10 | 4 | 3.7 | +1.3 |
3 | 3 | 9 | 9 | 5.0 | -2 |
4 | 8 | 32 | 16 | 6.3 | 1.7 |
5 | 7 | 35 | 25 | 7.6 | -0.6 |
∑X=15 | ∑Y=25 | ∑XY=88 | ∑X 2=55 | Trend Values | ∑(Y-
|
The equation of least square line Y=a +bX
Normal equation for ‘a’ ∑Y=na +b 25=5a+15b —- (1)
Normal equation for ‘b’ ∑XY = a∑X+b∑X2 88=15a+55b —-(2)
Eliminate a a from equation (1) and (2), multiply equation (2) by 3 and subtract from equation (2).
Eliminate a from equation (1) and (2), multiply equation (2) by (3) and subtract from equation (2). Thus, we get the values of a and b
Here a=1.1 and b=1.3, the equation of least square line becomes
Y=1.1+1.3X
Example 2:
using least square method to fit a straight line of the following data
X | 8 | 2 | 11 | 6 | 5 | 4 | 12 | 9 | 6 | 1 |
y | 3 | 10 | 3 | 6 | 8 | 12 | 1 | 4 | 9 | 14 |
Solution:
First we calculate 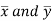 for the given data
for the given data
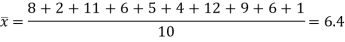
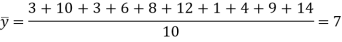
Now we calculate 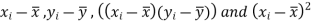
i |
|
|
|
|
|
|
1 | 8 | 3 | 1.6 | -4 | -6.4 | 2.56 |
2 | 2 | 10 | -4.4 | 3 | -13.2 | 19.36 |
3 | 11 | 3 | 4.6 | -4 | -18.4 | 21.16 |
4 | 6 | 6 | -0.4 | -1 | 0.4 | 0.16 |
5 | 5 | 8 | -1.4 | 1 | -1.4 | 1.96 |
6 | 4 | 12 | -2.4 | 5 | -12 | 5.76 |
7 | 12 | 1 | 5.6 | -6 | -33.6 | 31.36 |
8 | 9 | 4 | 2.6 | -3 | -7.8 | 6.76 |
9 | 6 | 9 | -0.4 | 2 | -0.8 | 0.16 |
10 | 1 | 14 | -5.4 | 7 | -37.8 | 29.16 |
|
|
|
|
|
|
|
Calculate the slope
m = 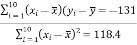 = -131/118.4
= -131/118.4 
calculate the y-intercept
use the formula to calculate the y-intercept
b = 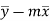
= 7-(-1.1*6.4)
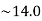
The required line equation is
Y= -1.1x+14.0
Determine the constants a and b by the method of least square such that 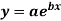
X | 2 | 4 | 6 | 8 | 10 |
y | 4.077 | 11.084 | 30.128 | 81.897 | 222.62
|
Solution:
The given relation is 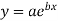
Taking logarithms on both sides we get,
log y = log a+ bx…. (1)
let,
log y = Y
x = X
log a = A
b = B
now we have,
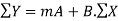 …. (2)
…. (2)
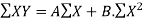 …. (3)
…. (3)
Now we need to find 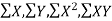
X=x | Y =ln(y) |
| xy |
2 | 1.405 | 4 | 2.810 |
4 | 2.405 | 16 | 9.620 |
6 | 3.405 | 36 | 20.430 |
8 | 4.405 | 44 | 35.240 |
10 | 5.405 | 100 | 54.050 |
|
|
|
|
|
|
|
|
The normal equations to fit the straight line is
Y = logey
Y= ln(y)
17.025 = 5A +30B…. (4) 
122.150 = 30A+220B…. (5)
By solving 4 and 5 we get
30A +180B = 102.15… (4)
30A+220B = 122.150… (5)
We get a = 0.405, b = 0.5
A =log a 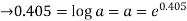
a = 1.499
since we have X=x and Y=y
log y=Y,
And we know y= aebx
Y = (1.499) e0.5x is the required exponential curve.
Example 2:
Fit the curve of the form y= aebx for the following data
X | 0 | 2 | 4 |
y | 8.12 | 10 | 31.82 |
Solution:
The given relation is 
Taking logarithms on both sides we get,
log y = log a+ bx logee…. (1)
the required normal equations are,
 …. (2)
…. (2)
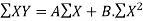 …. (3)
…. (3)
We have n=3
x | y | Y= logey | xy | X2 |
0 | 8.12 | 2.0943 | 0 | 0 |
2 | 10 | 2.3026 | 4.6052 | 4 |
4 | 31.82 | 3.4601 | 13.8404 | 16 |
|
|
|
|
|
The normal equations become
3A +6b = 7.8750
6A + 20 b = 18.4456
By solving the above two equations we get
A = 1.361 and b = 0.3415
Since A =logea 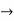 a = e1.361 = 6.9317
a = e1.361 = 6.9317
The curve of the fit is 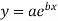
Thus, the required equation is,
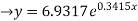
Second order curve: A plane curve whose rectangular Cartesian coordinates fulfil an algebraic calculation of the second degree:
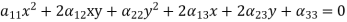
non-degenerate curves:
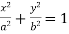 , ellipses (cf. Ellipse);
, ellipses (cf. Ellipse);
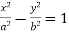 , hyperbolas (cf. Hyperbola);
, hyperbolas (cf. Hyperbola);
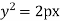 , parabolas (cf. Parabola);
, parabolas (cf. Parabola);
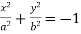 , imaginary ellipses;
, imaginary ellipses;
degenerate curves:
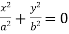 , pairs of imaginary intersecting lines;
, pairs of imaginary intersecting lines;
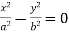 , pairs of real intersecting lines;
, pairs of real intersecting lines;
 , pairs of real parallel lines;
, pairs of real parallel lines;
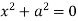 , pairs of imaginary parallel lines;
, pairs of imaginary parallel lines;
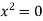 , a pair of coincident real lines.
, a pair of coincident real lines.
A second-order curve that has a unique centre of symmetry (the centre of the second-order curve) is named a central curve. The coordinates of the centre of a second-order curve are determined by the explanation of the system
|
A second-order curve without a centre of symmetry or with an indefinite centre is named a non-central curve.
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Y | 2 | 6 | 7 | 8 | 10 | 11 | 11 | 10 | 9 |
Solution:
X |
|
|
|
|
|
|
|
1 | -4 | 2 | 16 | -64 | 256 | -8 | 32 |
2 | -3 | 6 | 9 | -27 | 81 | -8 | 54 |
3 | -2 | 7 | 4 | -8 | 16 | -14 | 28 |
4 | -1 | 8 | 1 | -1 | 1 | -8 | 8 |
5 | 0 | 10 | 0 | 0 | 0 | 0 | 0 |
6 | 1 | 11 | 1 | 1 | 1 | 11 | 11 |
7 | 2 | 11 | 4 | 8 | 16 | 22 | 44 |
8 | 3 | 10 | 9 | 27 | 81 | 30 | 90 |
9 | 4 | 9 | 16 | 64 | 256 | 36 | 144 |
N=0 |
|
|
|
|
|
|
|
∑Y i =Na + b ∑X i +c∑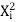
∑X i Y i =a ∑X i +b∑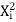 +c∑
+c∑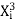
∑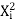 Y i =a∑
Y i =a∑ +b∑
+b∑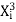 +c∑
+c∑
The required parabola is of the form y= ax2+bx+c
∴74=9a+b (0) +60c∴9a+60c=74…(i)
51=a (0) +60b+0c ∴60b=51 ∴b=5160 =0.85411=60a+0b+708 c∴60a+708c=411…(ii)
Solving (i) and (ii) simultaneously, we get
a=10.004, c=-0.267
The Equation of parabola is therefore,
y=10.004+0.85X−0.267X 2
=10.004+0.85(x−5) −0.267(x−5) 2
=10.004+0.85x−4.25−0.267(x 2 −10x+25)
=10.004+0.85x−4.25−0.267x 2 +2.67x−6.675
∴ y = −0.921+3.52x−0.267x 2
Example 2:
Find the least square approximation of degree two to the data
X | 0 | 1 | 2 | 3 | 4 |
Y | -4 | -1 | 4 | 11 | 20 |
Solution:
X | y | xy |
|
|
|
|
0 | -4 | 0 | 0 | 0 | 0 | 0 |
1 | -1 | -1 | 1 | -1 | 1 | 1 |
2 | 4 | 8 | 4 | 16 | 8 | 16 |
3 | 11 | 33 | 9 | 99 | 27 | 81 |
4 | 20 | 80 | 16 | 320 | 64 | 256 |
|
|
|
|
|
|
|
the normal equations are:
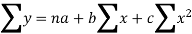
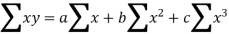
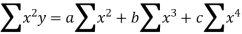
Here,
n = 5, 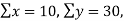
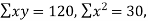
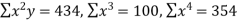
by substituting all the above values in normal equations we get,
30 = 5a+10b+30c
120=10a+30b+100c
434=30a+100b+354c
By solving the above equations, we get
a = -4, b=2, c=1.
Therefore, the required polynomial is
Y= -4x+2x+x2 and errors =0
Reference