UNIT 5
Isometric projections
Isometric projection is a type of pictorial projection in which the three dimensions of a solid are not only shown in one view, but their actual sizes can be measured directly from it.
If a cube is placed on one of its corners on the ground with a solid diagonal perpendicular to the V.P., the front view is the isometric projection of the cube. The step-by-step construction is shown in fig.1.
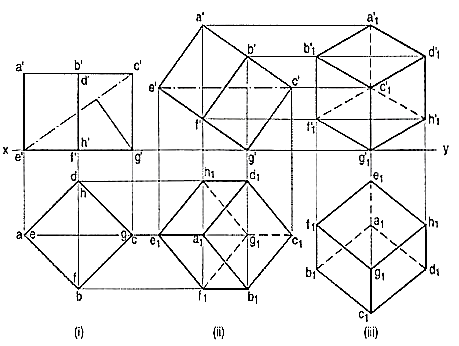
To draw the projections of a cube of 25 mm long edges resting on the ground on one of its corners with a solid diagonal perpendicular to the V.P., assume the cube to be resting on one of its faces on the ground with a solid diagonal parallel to the V.P.
(I) draw a square abed in the top view with its sides inclined at 45° to xy. The line ac representing the solid diagonals AG and CE is parallel to xy. Project the front view.
(ii) Tilt the front view about the corner g' so that the line e' c' becomes parallel to xy. Project the second top view. The solid diagonal CE is now parallel to both the H.P. And the V.P.
(iii) Reproduce the second top view so that the top view of the solid diagonal, viz. e1 c1 is perpendicular to xy. Project the required front view.
Figure shows the front view of the cube in the above position, with the corners named in capital letters. Its careful study will show that
(a) All the faces of the cube are equally inclined to the V.P. And hence, they are seen as similar and equal rhombuses instead of squares.
(b) The three lines CB, CD and CG meeting at C and representing the three edges of the solid right-angle are also equally inclined to the V.P. And are therefore, equally fore shortened. They make equal angles of 120° with each other. The line CG being vertical, the other two lines CB and CD make 30° angle each, with the horizontal.

(c) All the other lines representing the edges of the cube are parallel to one or the other of the above three lines and are also equally foreshortened.
(d) The diagonal BO of the top face is parallel to the V.P. And hence, retains its true length.
This chapter deals with various topics of isometric projection as shown below:
1. Isometric axes, lines and planes
2. Isometric scale
3. Isometric drawing or isometric view
4. Isometric graph.
Isometric axes, lines and planes:
The three lines CB, CD and CG meeting at the point C and making 120° angles witheach other are termed isometric axes. The lines parallel to these axes are called isometriclines. The planes representing the faces of the cube as well as other planes parallel tothese planes are calledisometric planes.
Isometric scale:
As all the edges of the cube are equally foreshortened, the square faces are rhombuses. The rhombus ABCD (fig. 2) shows the isometric projection ofthe top square face of the cube in which BO is the true length of the diagonal.
Construct a square BQDP around BO as a diagonal. Then BP shows the truelength of BA.
In triangle ABO, 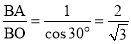
In triangle PBO, 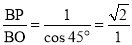
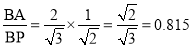
The ratio, 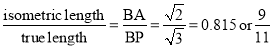 .
.
Thus, the isometric projection is reduced in the ratio 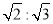 , i.e. the isometric lengths are 0.815 of the true lengths.
, i.e. the isometric lengths are 0.815 of the true lengths.
Therefore, while drawing an isometricprojection, it is necessary to convert truelengths into isometric lengths for measuringand marking the sizes. This is convenientlydone by constructing and making use ofan isometric scale as shown below.
a) Draw a horizontal line BO of anylength (fig. 3). At the end B,draw lines BA and BP, such thatL OBA = 30° and L OBP = 45°.Mark divisions of true lengthon the line BP and from eachdivision-point, draw verticals toBO meeting BA at respective points.The divisions thus obtained on BAgive lengths on isometric scale.
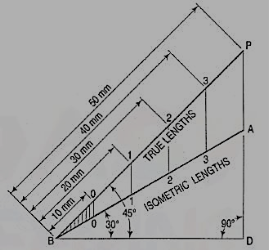
Figure 3
(b) The same scale may also be drawn with divisions of natural scale on a horizontal line AB (fig. 4). At the ends A and B, draw lines AC and BC making 15° and 45° angles with AB respectively, and intersecting each other at C.
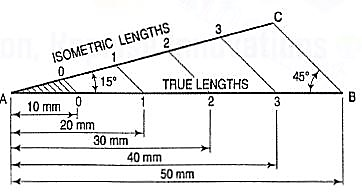
Figure 4
From division-points of true lengths on AB, draw lines parallel to BC and meeting AC at respective points. The divisions along AC give lengths to isometric scale.
The lines BO and AC (fig. 2) represent equal diagonals of a square face of the cube, but are not equally shortened in isometric projection. BO retains its true length, while AC is considerably shortened. Thus, it is seen that lines which are not parallel to the isometric axes are not reduced according to any fixed ratio. Such lines are called non-isometric lines. The measurements should, therefore, be made on isometric axes and isometric lines only. The non-isometric lines are drawn by locating positions of their ends on isometric planes and then joining them.
Isometric drawing or Isometric view
If the foreshortening of the isometric lines in an isometric projection is disregardedand instead, the true lengths are marked, the view obtained [fig. 5(iii)] will beexactly of the same shape but larger in proportion (about 22.5%) than that obtainedusing the isometric scale [fig. 5(ii)]. Due to the ease in constructionand the advantage of measuring the dimensions directly from the drawing, it hasbecome a general practice to use the true scale instead of the isometric scale.
To avoid confusion, the view drawn with the true scale is called isometricdrawing or isometric view, while that drawn with the use of isometric scale iscalled isometric projection.
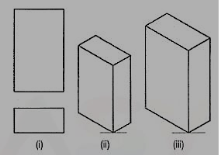
Figure 5
Referring again to fig. 2, the axes BC and CD represent the sides of a right angle in horizontal position. Each of them together with the vertical axis CG, represents the right angle in vertical position. Hence, in isometric view of any rectangular solid resting on a face on the ground, each horizontal face will have its sides parallel to the two sloping axes; each vertical face will have its vertical sides parallel to the vertical axis and the other sides parallel to one of the sloping axes.
In other words, the vertical edges are shown by vertical lines, while the horizontaledges are represented by lines, making 30° angles with the horizontal. These lines arevery conveniently drawn with the T-square and a 30°-60° set-square or drafter.
Isometric Graph:
An isometric graph as shown in fig. 6 facilitates the drawing of isometric view of an object. Students are advised to make practice for drawing of isometric view using such graphs.
- Isometric Projection of objects having non- isometric lines
When an object contains inclined edges which in the isometric view would be shown by non-isometric lines, the view may be drawn by using any one of the following methods:
(i) box method or
(ii) co-ordinate or offset method.
(i) Box method: This method is used when the non-isometric lines or their ends lie in isometric planes. The object is assumed to be enclosed in a rectangular box. Initially, the box is drawn in isometric. The ends of the lines for the inclined edges are then located by measuring on or from the outlines of the box.
Problem:
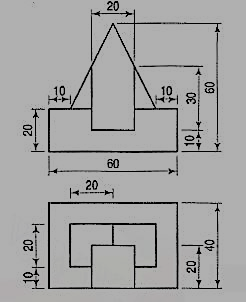
1. Three views of a block are given in fig. 16 (i). Draw its isometric view.
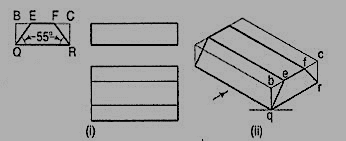
Figure 16
(i) Enclose the block in a rectangular box.
(ii) Draw the isometric view of the box [fig. 16 (ii)].
(iii) Mark points e and f on the line be such that be = BE and fc = FC.
(iv) Complete the required view as shown.
2. Draw the isometric view of the frustum of the hexagonal pyramid shown in fig. 17 (i).
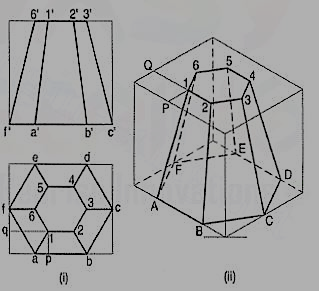
Figure 17
(i) Enclose the front view and the top view in rectangles.
(ii) Draw the isometric view of the rectangular box [fig. 17 (ii)]. Locate the six points of the base of the frustum on the sides of the bottom of the box. The upper six points on the top surface of the box are located by drawing isometric lines, e.g. P1 and Q1 intersecting at a point 1.
(iii) Join the corners and complete the isometric view as shown.
2. Co- ordinate or Offset method:
This method is adopted for objects in which neither non-isometric lines nor their ends lie in isometric planes.
Perpendiculars are dropped from each end of the edge to a horizontal or a vertical reference plane. The points at which the perpendiculars meet the plane, are located by drawing co-ordinates or offsets to the edges of the plane.
Problem:
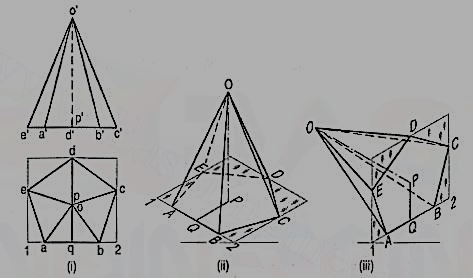
1. Draw the isometric view of the pentagonal pyramid, the projections of which are given in fig. 18 (i).
(i) Enclose the base (in the top view) in an oblong.
(ii) Draw an offset oq (i.e. pq) on the line ab.
(iii) Draw the isometric view of the oblong and locate the corners of the base in it [fig. 18 (ii)].
(iv) Mark a point Q on the line AB such that AQ = aq. From Q, draw a line QP equal to qo and parallel to 2C. At P, draw a vertical OP equal to o'p'.
(v) Join O with the corners of the base, thus completing the isometric view of the pyramid.
Fig. 18(iii) shows the isometric view of the same pyramid with its axis in horizontal position.
Isometric Projection of Spherical Parts
The orthographic view of a sphere seen from any direction is a circle of diameter equal to the diameter of the sphere. Hence, the isometric projection of a sphere is also a circle of the same diameter as explained below.
The front view and the top view of a sphere resting on the ground are shown in fig. 25 (i). C is its centre, D is the diameter and P is the point of its contact with the ground.
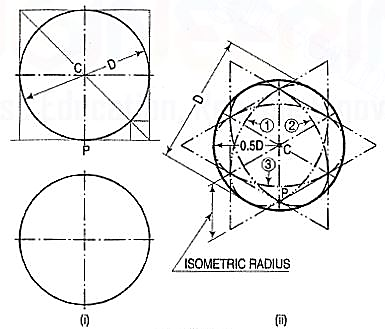
Figure 25
Assume a vertical section through the centre of the sphere. Its shape will be a circle of diameter D. The isometric projection of this circle is shown in fig. 25 (ii) by ellipses 1 and 2, drawn in two different vertical positions around the same centre C. The length of the major axis in each case is equal to D. The distance of the point P from the centre C is equal to the isometric radius of the sphere.
Again, assume a horizontal section through the centre of the sphere. The isometric projection of this circle is shown by the ellipse 3, drawn in a horizontal position around the same centre C. In this case also, the distance of the outermost points on the ellipse from the centre C is equal to O.5D.
Thus, in an isometric projection, the distances of all the points on the surface of a sphere from its centre, are equal to the radius of the sphere.
Hence, the isometric projection of a sphere is a circle whose diameter is equal to the true diameter of the sphere.
Also, the distance of the centre of the sphere from its point of contact with the ground is equal to the isometric radius of the sphere, viz. CP.
It is, therefore, of the utmost importance to note that, isometric scale must invariably be used, while drawing isometric projections of solids in conjunction with spheres or having spherical parts.
Problem:
Draw the isometric projection of a sphere resting centrally on the top of a square prism, the front view of which is shown in fig. 26 (i).
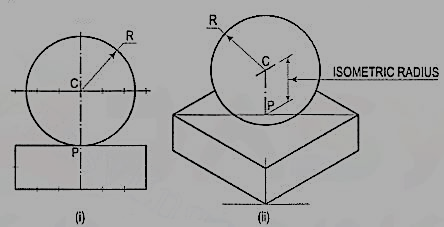
Figure 26
(i) Draw the isometric projection (using isometric scale) of the square prism and locate the centre P of its top surface [fig. 26 (ii)].
(ii) Draw a vertical at P and mark a point C on it, such that PC = the isometric radius of the sphere.
(iii) With C as centre and radius equal to the radius of the sphere, draw a circle which will be the isometric projection of the sphere.
Problems:
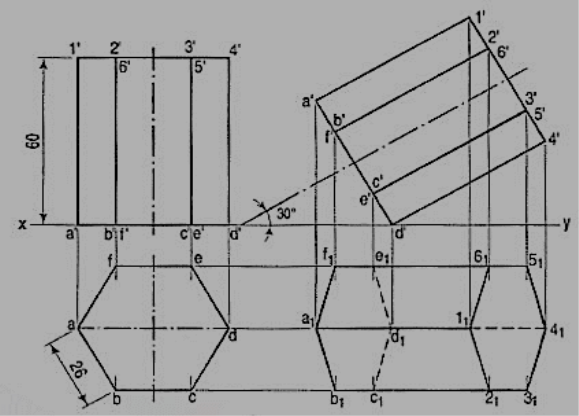
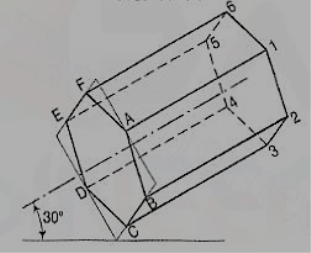
1. A hexagonal prism having the side of base 26 mm and the height of 60 mm is resting on one of the comer of the base and its axis is inclined to 30° to the H.P. Draw its projections and prepare the isometric view of the prism in the above stated condition.
(i) Draw the projections of the prism as shown in figure 27.
(ii) Construct the isometric view as shown in fig. 28.
2. The orthographic projections of the object is shown in fig. 29. Draw the isometric view of the object.