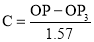UNIT 1
Fundamentals of Engineering Graphics & Engineering Curves
- Fundamentals of Engineering Graphics:
- Introduction to Drawing instruments and their uses
Drawing paper is made up of variety of qualities and manufactured in sheets or rolls. White drawing papers that will not turn yellow with age or exposure are used for finished drawings, maps, charts, and drawings for photographic reproduction. For pencil layouts and working drawings buff detail papers are preferred as they are easier on the eyes compared to white papers.
Tracing papers are thin papers, natural or transparent, on which drawings are traced, in pencil or ink, and from which blueprints or similar contact prints can be made. In most drafting rooms original drawings are penciled on tracing papers, and blueprints are made directly from these drawings, a practice increasingly successful because of improvements both in papers and in printing.
The best thumbtacks are made with thin heads and steel points screwed into them. Cheaper ones are made by stamping. Use tacks with tapering pins of small diameter and avoid flat-headed (often colored) map pins, as the heads are too thick and the pins rather large.
The basic instrument is the graphite lead pencil, made in various hardness’s. Each manufacturer has special methods of processing design to make the lead strong and yet give a smooth clear line.
In the left there is an ordinary pencil, with the lead set in wood and the other is a semi-automatic pencil with thinner leads. Both are fine but have the disadvantage that in use, the wood must be cut away to expose the lead (a time-consuming job), and the pencil becomes shorter and shorter until the last portion of it is to be discarded. Where as semi automatic pencils, with a chuck to clamp and hold the lead, are more convenient, has a plastic handle and changeable tip (for indicating the grade of lead).
Drawing pencils are graded by numbers and letters from 6B which is very soft and black, to 5B, 4B, 3B, 2B, B, and HB to F, the medium grade; then H, 2H, 3H, 4H, 5H, 6H, 7H, and 8H to 9H, the hardest. The soft (B) grades are used primarily for sketching and rendered drawings and the hard (H) grades for instrument drawings.
After the wood of the ordinary pencil is cut away with a pocketknife or mechanical sharpener, the lead must be formed to a long, conic point.
A pencil pointer is a tool for sharpening a pencil’s writing point by shaving away its worn surface.
The Ruby pencil eraser, large size with beveled ends, is the standard. This eraser not only removes pencil lines effectively but is better for ink, as it removes ink without seriously damaging the surface of paper or cloth.
Art gum or a soft-rubber eraser is useful for cleaning paper and cloth of finger marks and smears that spoil the appearance of the completed drawing.
The penholder should have a grip of medium size, small enough to enter the mouth of a drawing-inkbottle easily yet not as small as to cramp the fingers while in use. A size slightly larger than the diameter of a pencil is good.
Triangles, are made of transparent hard or other plastic material. Through internal strains they sometimes lose their accuracy. Triangles should be kept flat to prevent warping. For ordinary work, a 6- or 8-in. 45° and a 10-in. 30-60° are good sizes.
The fixed-head T square, is used for all ordinary work. It should be of hardwood, and the blade should be perfectly straight. The transparent-edged blade is much the best. A draftsman will have several fixed-head squares of different lengths and will find an adjustable-head square of occasional use.
Curve rulers, called "irregular curves" or "French curves," are used to draw curved lines other than circular arcs. The patterns for these curves are laid out in parts of ellipse and spirals or other mathematical curves in various combinations. For the student, one ellipse curve of the general shape or one spiral, either a logarithmic spiral is a useful small curve.
We have so far, except for curves considered only the instruments needed for drawing straight lines. A major portion of any drawing is likely to be circles and circle arcs, and the so called “case” instruments are used for these.
It is used for laying off or transferring measurements.
Next is the large compass with lengthening bar and pen attachment. The three “bow” instruments are for smaller work. They are almost always made without the conversion feature.
The ruling pen is used for inking straight lines.
Protractor is used to measure angles up to 180°.
Engineering drawings are prepared on standard size drawing sheets. The correct shape and size of the object can be visualized from the understanding of not only its views but also from the various types of lines used, dimensions, notes, scale etc. For uniformity, the drawings must be drawn as per certain standard practice.
Drawing sheet layout
The layout of a drawing sheet used on the shop floor is shown in Fig.1. The layout suggested to students is shown in Fig.2.
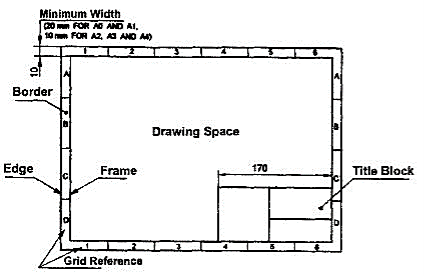
Figure 1 General features of a drawing sheet
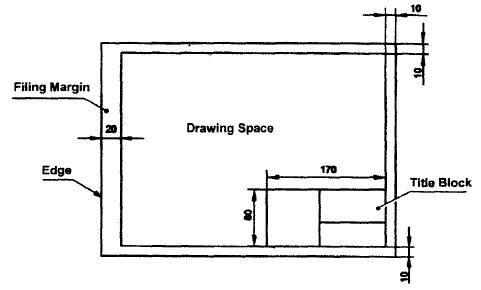
Figure 2 Layout of sheet for a class work
i) Sizes of Drawing Sheets
The standard drawing sheet sizes are arrived at on the basic Principal of x: y = 1: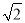
and xy = 1 where x and yare the sides of the sheet. For example, A0, having a surface area of 1 Sq. m; x = 841 mm and y = 1189 mm. The successive sizes are obtained by either by halving along the length or doubling the width, the area being in the ratio 1: 2. Designation of sizes is given in Fig.3 and their sizes are given in Table 1. For class work use of A2 size drawing sheet is preferred.
Table 1
Designation | Dimension, mm (Trimmed size) |
A0 | 841 × 1189 |
A1 | 594 × 841 |
A2 | 420 × 594 |
A3 | 297 × 420 |
A4 | 210 × 297 |
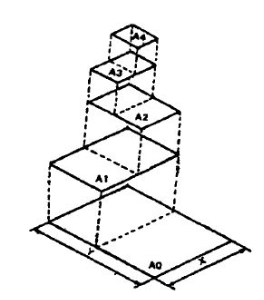
Figure 3
Title block
The title block should lie within the drawing space at the bottom right hand comer of the sheet. The title block can have a maximum length of 170 mm providing the following information.
1. Title of the drawing.
2. Drawing number.
3. Scale.
4. Symbol denoting the method of projection.
5. Name of the firm, and
6. Initials of staff who have designed, checked and approved.
The title block used on shop floor and one suggested for student’s class work are shown inFig.4& Fig. 5.
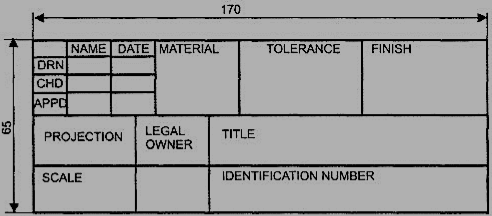
Figure 4 Shop floor drawing sheet layout
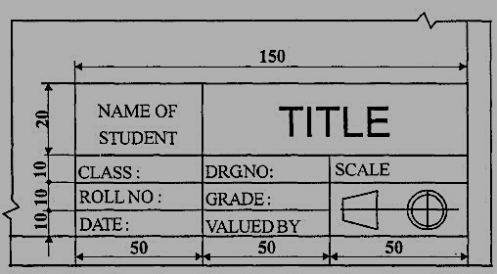
Figure 5 Students class work
Just as in English textbook the correct words are used for making correct sentences; in Engineering Graphics, the details of various objects are drawn by different types of lines. Each line has a definite meaning and sense to convey.
IS 10714 (Pint 20): 2001 (General principles of presentation on technical drawings) and SP 46:2003specify the following types oflines and their applications:
1. Visible Outlines, Visible Edges: (Continuous wide lines) the lines drawn to represent the visible outlines/ visible edges / surface boundary lines of objects should be outstanding in appearance.
2. Dimension Lines: (Continuous narrow Lines) Dimension Lines are drawn to mark dimension.
3. Extension Lines: (Continuous narrow Lines) There are extended slightly beyond the respective dimension lines.
4. Construction Lines: (Continuous narrow Lines) Construction Lines are drawn for constructing drawings and should not be erased after completion of the drawing.
5. Hatching / Section Lines: (Continuous Narrow Lines)
Hatching Lines are drawn for the sectioned portion of an object. These are drawn inclined at an angle of 45° to the axis or to the main outline of the section.
6. Guide Lines: (Continuous Narrow Lines)
Guide Lines are drawn for lettering and should not be erased after lettering.
7. Break Lines: (Continuous Narrow Freehand Lines)
Wavy continuous narrow line drawn freehand is used to represent break of an object.
8. Break Lines: (Continuous Narrow Lines with Zigzags)
Straight continuous arrow line with zigzags is used to represent break of an object.
9. Dashed Narrow Lines: (Dashed Narrow Lines)
Hidden edges / Hidden outlines of objects are shown by dashed lines of short dashes of equal lengths of about 3 mm, spaced at equal distances of about 1 mm. The points of intersection of these lines with the outlines / another hidden line should be clearly shown.
10. Center Lines: (Long-Dashed Dotted Narrow Lines)
Center Lines are drawn at the center of the drawings symmetrical about an axis or both the axes. These are extended by a short distance beyond the outline of the drawing.
11. Cutting Plane Lines:
Cutting Plane Line is drawn to show the location of a cutting plane. It is long-dashed dotted narrow line, made wide at the ends, bends and change of direction. The direction of viewing is shown by means of arrows resting on the cutting plane line.
12. Border Lines
Border Lines are continuous wide lines of minimum thickness 0.7 mm.
Figure 6 Types of lines
Table 2 Types of lines and their applications
Line | Description | General application |
| Continuous thick or continuous wide | Visible outlines, visible edges, main representation in diagrams, maps; system lines |
| Continuous thin (narrow) (straight or curved) | Imaginary lines of intersection; grid, dimension. Extension, projection, reference lines and hatching. |
| Continuous thin (narrow) freehand. | Limits of partial or interrupted views and sections, if the limit is not a chain thin line. |
| Continuous thin (narrow) with zigzags (straight) | Long break line |
 | Dashed thick (wide) | Line showing permissible of surface treatment. |
 | Dashed thin (narrow) | Hidden outline; hidden edges |
 | Chain thin Long-dashed dotted (narrow) | Centre line; lines of symmetry; trajectories; pitch circle of gears, pitch circle of holes. |
 | Chain thick or long - dashed (dotted) wide | Indication of lines or surfaces to which a special requirement applies. |
Line widths:
Line width means line thickness
Choose line widths according to the size of the drawing from the following range: 0.13, 0.18, 0.25, 0.35, 0.5, 0.7 and 1 mm.
Precedence of Lines
1. When a Visible Line coincides with a Hidden Line or Center Line, draw the Visible Line. Also, extend the Center Line beyond the outlines of the view.
2. When a Hidden Line coincides with a Center Line, draw the Hidden Line.
3. When a Visible Line coincides with a Cutting Plane, draw the Visible Line.
4. When a Center line coincides with a Cutting Plane, draw the Center Line and show the
Cutting Plane line outside the outlines of the view at the ends of the Center Line by thick dashes.
Drawing of a component, in addition to providing complete shape description, must also furnish information regarding the size description. These are provided through the distances between the surfaces, location of holes, nature of surface finish, type of material, etc. The expression of these features on a drawing, using lines, symbols, figures and notes is called dimensioning.
Principles of Dimensioning
Some of the basic principles of dimensioning are given below.
1. All dimensional information necessary to describe a component clearly and completely shall be written directly on a drawing.
2. Each feature shall be dimensioned once only on a drawing, i.e., dimension marked in one view need not be repeated in another view.
3. Dimension should be placed on the view where the shape is best seen (Fig.7)
4. As far as possible, dimensions should be expressed in one unit only preferably in millimeters, without showing the unit symbol (mm).
5. As far as possible dimensions should be placed outside the view (Fig. 8).
6. Dimensions should be taken from visible outlines rather than from hidden lines (Fig. 9).
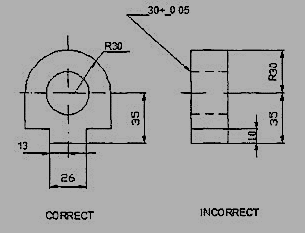
Figure 7
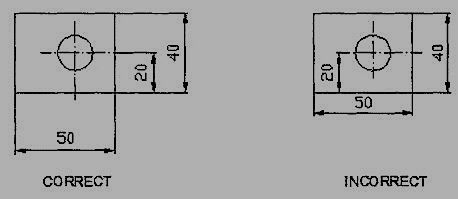
Figure 8
Figure 9
7. No gap should be left between the feature and the start of the extension line (Fig.10).
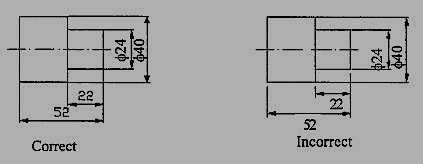
Figure 10 Marking of Extension lines
8. Crossing of center lines should be done by a long dash and not a short dash (Fig.11).
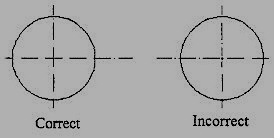
Figure 11 Crossing of Centre lines
Execution of dimensions:
1. Projection and dimension lines should be drawn as thin continuous lines. Projection lines should extend slightly beyond the respective dimension line. Projection lines should be drawn perpendicular to the feature being dimensioned. If the space for dimensioning is insufficient, the arrow heads may be reversed, and the adjacent arrow heads may be replaced by a dot (Fig.12). However, they may be drawn obliquely, but parallel to each other in special cases, such as on tapered feature (Fig.13).
Figure 12 Dimensioning in narrow spaces
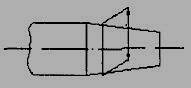
Figure 13 dimensioning a tapered feature
2. A leader line is a line referring to a feature (object, outline, and dimension). Leader lines should be inclined to the horizontal at an angle greater than 30°. Leader line should terminate,
(a) With a dot, if they end within the outline of an object (Fig 14(a).
(b) With an arrow head, if they end on outside of the object (Fig 14(b)).
(c) Without a dot or arrow head, if they end on dimension line (Fig.14(c)).
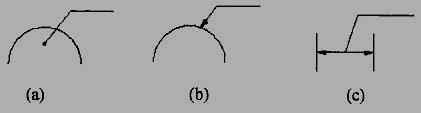
Figure 14 Termination of leader lines
Dimension Termination and Origin Indication
Dimension lines should show distinct termination in the form of arrow heads or oblique strokes or where applicable an origin indication (Fig.14). The arrow head included angle is 15°. The origin indication is drawn as a small open circle of approximately 3 mm in diameter. The proportion length to depth 3: 1 of arrow head is shown in Fig.15.
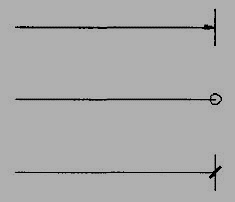
Figure 15 Termination of dimension lines
Figure 16 Proportions of an arrow head
Methods of Indicating Dimensions
The dimensions are indicated on the drawings according to one of the following two methods.
- Method I (Aligned method)
Dimensions should be placed parallel to and above their dimension lines and preferably at the middle, and clear of the line. (Fig. 17).
Figure 17
Dimensions may be written so that they can be read from the bottom or from the right side of the drawing. Dimensions on oblique dimension lines should be oriented as shown in Fig.18a and except where unavoidable, they shall not be placed in the 30° zone. Angular dimensions are oriented as shown in Fig.18b.
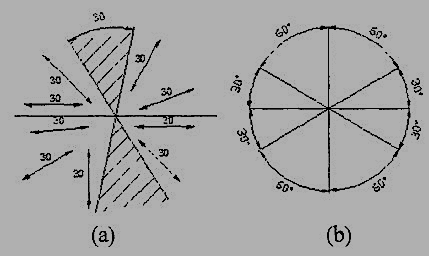
Figure 18 Angular dimensioning
2. Method 2 ( Uni-directional method)
Dimensions should be indicated so that they can be read from the bottom of the drawing only. Non-horizontal dimension lines are interrupted, preferably in the middle for insertion of the dimension (Fig.19a).
Angular dimensions may be oriented as in (Fig.19b)
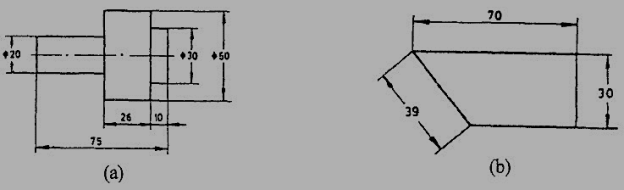
Figure 19Uni-directional method
A) Engineering curves:
Conic sections- Ellipse(excluding focus directrix method), Parabola, Hyperbola & involute
The section obtained by intersection of a right circular cone by a plane in different positions relative to the axis of the cone are called conics.
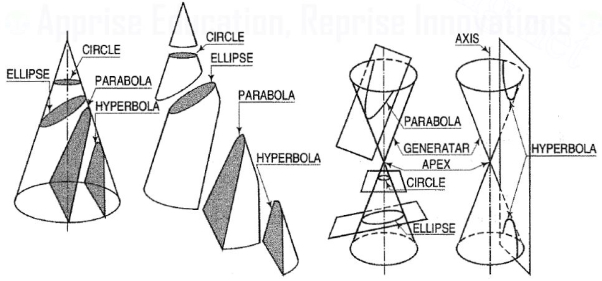
Conic sections are always "smooth". More precisely, they never contain any inflection points. This is important for many applications, such as aerodynamics, civil engineering, mechanical engineering, etc.
The conic may be defined as the locus of a point in a plane, wherein the ratio of its distance from a fixed point and a fixed straight line is always constant. The fixed point is called the focus and the fixed line, the directrix.
The ratio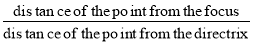 
is called eccentricity and is denoted by ‘e’. It is always less the 1 for ellipse, equal to 1 for parabola and greater than 1 for hyperbola.
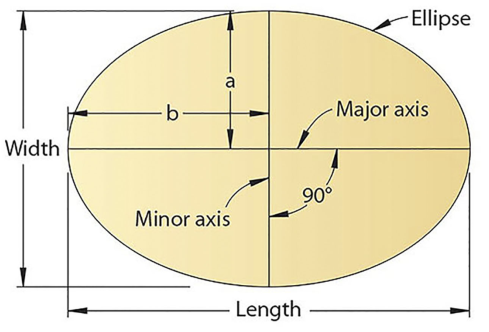
Ellipse:
Use of elliptical curves is made in arches, bridges, dams, monuments, man holes, etc. Mathematically an ellipse can be described by equation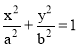 
.
Here ‘a’ and ‘b’ are half the length of major and minor axes of ellipse and x and y are co-ordinates.
Parabola:
Use of parabolic curves is made in arches, bridges, sound reflectors, light reflectors, etc. Mathematically it can be described by an equation 
or 
.
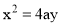Involute:
The involute is a curve traced out by an end of a piece of thread unwound froma circle or a polygon, the thread being kept tight. It may also be defined as acurve traced out by a point in astraight line which rolls without slipping along acircle or a polygon.
It is used as teeth profile of gear wheel.
Mathematically it can be described as by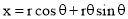 
, 
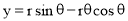, where “r” is the radius of the circle.
Spiral:
If a line rotates in a plane about one of its ends and if at the same time, a point moves along the line continuously in one direction, the curve traced out by the moving point is called a spiral. The point about which the line rotates is called a pole.
The line joining any point on the curve with the pole is called the radius vector and the angle between this line and the line in its initial position is called the vectorial angle.
Archemedian spiral:
It is a curve traced out by a point moving in such a way that its movement towards and away from the pole is uniform with the increase of the vectorial angle from the starting line.
The use of this curve is made in teeth profiles of helical gears, profile of cams, etc.
Cycloid curves- only Cycloid.
Cycloid is a curve generated by a point on the circumference of a circle which rolls along a straight line. It can be described by an equation,
y = a (1 - cosθ) or x = a (θ - sinθ)
To construct a cycloid, given the diameter of the generating circle.
(i) With centre C and given radius R, draw a circle. Let P be the generating point.
(ii) Draw a line PA tangential to and equal to the circumference of the circle.
(iii) Divide the circle and the line PA into the same number of equal parts, say 12,and mark the division-points as shown.
(iv) Through C, draw a line CB parallel and equal to PA.
(v) Draw perpendiculars at points 1, 2 etc. cutting CB at points C1, C2 etc.
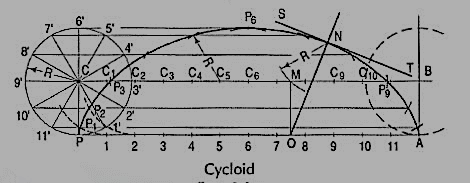
Assume that the circle starts rolling to the right. When point 1' coincides with 1, centre C will move to C1. In this position of the circle, the generating point P will have moved to position P1 on the circle, at a distance equal to P'1 from point 1. It is evident that P1 lies on the horizontal line through 1' and at a distance R from C1. Similarly, P2 will lie on the horizontal line through 2' and at the distance R from C2.
Construction:
(vi) Through the points 1 ', 2' etc. draw lines parallel to PA.
(vii) With centres C1, C2 etc. and radius equal to R, radius of generating circle, draw arcs cutting the lines through 1 ', 2' etc. at points P1, P2 etc. respectively. Draw a smooth curve through points P, P1, P2 …. A. This curve is the required cycloid.
Normal and tangent to a cycloid curve: The rule for drawing a normal to all cycloidal curves:
The normal at any point on a cycloidal curve will pass through the corresponding point of contact between the generating circle and the directing line or circle. The tangent at any point is perpendicular to the normal at that point.
Involute:
The involute is a curve traced out by an end of a piece of thread unwound from a circle or a polygon, the thread being kept tight. It may also be defined as a curve traced out by a point in a straight line which rolls without slipping along a circle or a polygon. Involute of a circle is used as teeth profile of gear wheel. Mathematically it can be described by x = rcosθ + rθsinθ, y = rsinθ - rθcosθ, where "r" is the radius of a circle.
Problem: To draw an involute of a given circle.
With centre C, draw the given circle. Let P be the starting point, i.e. the end of the thread.
Suppose the thread to be partly unwound, say upto a point 1. P will move to a position P1 such that 1P1 is tangent to the circle and is equal to the arc 1 P. P1 will be a point on the involute.
Construction:
(i) Draw a line PQ, tangent to the circle and equal to the circumference of the circle.
(ii) Divide PQ and the circle into 12 equal parts.
(iii) Draw tangents at points 1, 2, 3 etc. and mark on them points P1, P2, P3 etc. such that 1P1 = P1', 2P2 = P2', 3P3 = P3' etc.
Draw the involute through the points P, P1, P2 .... Etc.
Normal and tangent to an involute:
The normal to an involute of a circle is tangent to that circle.
Problem:
To draw a normal and a tangent to the involute of a circle at a point N on it.
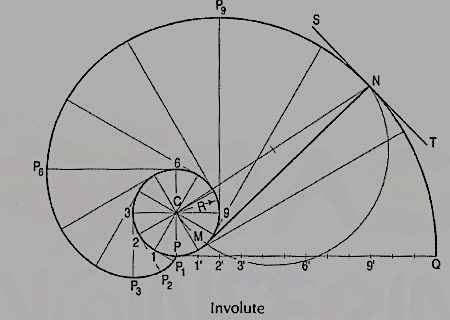
(i) Draw a line joining C with N.
(ii) With CN as diameter describe a semi-circle cutting the circle at M.
(iii) Draw a line through N and M. This line is the normal. Draw a line ST, perpendicular to NM and passing through N. ST is the tangent to the involute.
Problem: Trace the paths of the ends of a straight-line AP, 100 mm long, when it rolls, without slipping, on a semi-circle having its diameter AB, 75 mm long. (Assume the line AP to be tangent to the semi-circle in the starting position.)
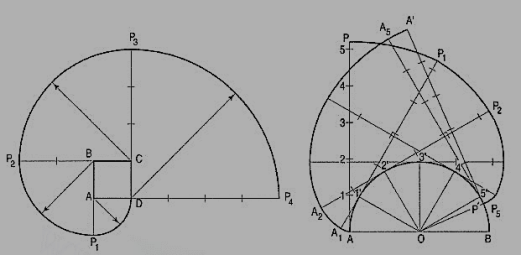
(i) Draw the semi-circle and divide it into six equal parts.
(ii) Draw the line AP and mark points 1, 2 etc. such that A1 = arc A1 ', A2 = arc A2' etc. The last division SP will be of a shorter length. On the semi-circle, mark a point P' such that S'P' = SP.
(iii) At points 1 ', 2' etc. draw tangents and on them, mark points P1, P2 etc. such that 1' P1 = 1P, 2' P2 =2P .... And 5' P5 = 5' P6 =SP. Similarly, mark pointsA1, A2 etc. such that A11'= A1, A22' = A2 .... And A'p'= AP. Draw the required curves through points P,P1 .... And P', and through points A, A1 .... And A'.
If AP is an inelastic string with the end A attached to the semicircle, the end P will trace out the same curve PP' when the string is wound round the semi-circle.
Involute:
The involute is a curve traced out by an end of a piece of thread unwound from a circle or a polygon, the thread being kept tight. It may also be defined as a curve traced out by a point in a straight line which rolls without slipping along a circle or a polygon.
It is used as teeth profile of gear wheel.
Mathematically it can be described as by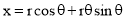 
, 
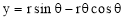, where “r” is the radius of the circle.
An involute is a curve traced by a point on a perfectly flexible string, while unwinding from around a circle or polygon the string being kept taut (tight). It is also a curve traced by a point on a straight line while the line is rolling around a circle or polygon without slipping.
To draw an involute of a given square.
1. Draw the given square ABCD of side a.
2. Taking A as the starting point, with centre B and radius BA=a, draw an arc to intersect the
Line CB produced at Pl.
3. With Centre C and radius CP1 =2 a, draw on arc to intersect the line DC produced at P 2.
4. Similarly, locate the points P3 and P4.
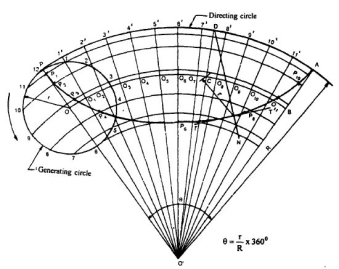
The curve through A, P1, P2, P3 and P4 is the required involute.
A P4 is equal to the perimeter of the square.
AP is a rope 1.50-metre-long, tied to peg at A as shown in fig. 24. Keeping it always tight, the rope is wound round the pole. Draw the curve traced out by the end P. Use scale 1 :20.
Draw given figure to the scale.
(ii) From A, draw a line passing through 1. A as centre and AP as radius, draw the arc intersecting extended line A1' at P0. Extend the side 1-2, 1 as centre and 1 'Po as radius, draw the arc to intersect extended line 1-2 at P1.
(iii) Divide the circumference of the semicircle into six equal parts and label it as 2, 3, 4, 5, 6, 7 and 8.
(iv) Draw a tangent to semicircle from 2 such that 2'-P1 = 2'-P2 . Mark 8' on this tangent such that 2'-8' = nR. Divide 2'-8' into six equal parts.
(v) Similarly draw tangents at 3, 4, 5, 6, 7 and 8 in anti-clockwise direction such that 3-P3 = 3'-9', 4-P4 = 4'-9', 5-P5 = 5'-9', 6-P6 = 6'-9', 7-P7 = 7'-9', 8-P8 = 8'-9' and 8-P9 = 8'-9' respectively.
(vi) Join P1, P2, ....• , P9 with smooth curve.
Spiral:
If a line rotates in a plane about one of its ends and if at the same time, a point moves along the line continuously in one direction, the curve traced out by the moving point is called a spiral. The point about which the line rotates is called a pole.
The line joining any point on the curve with the pole is called the radius vector and the angle between this line and the line in its initial position is called the vectorial angle.
Archemedian spiral:
It is a curve traced out by a point moving in such a way that its movement towards and away from the pole is uniform with the increase of the vectorial angle from the starting line.
The use of this curve is made in teeth profiles of helical gears, profile of cams, etc.
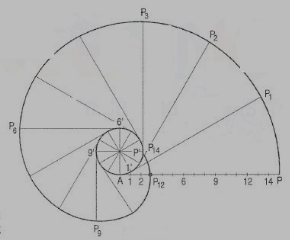
To construct an Archemedian spiral of 
convolutions given the greatest and the shortest radii.
Let O be the pole, OP the greatest radius and OQ the shortest radius.
(i) With centre O and radius equal to OP, draw a circle. OP revolves around0 for 
revolutions. During this period, P moves towards 0, the distance equal to (OP - OQ) i.e. QP.
(ii) Divide the angular movements of OP, viz 
revolutions i.e. 540°and the line QP into the same number of equal parts, say 18 (one revolution divided into 12 equal parts).
When the line OP moves through one division, i.e. 30°, the point P will move towards O by a distance equal to one division of QP to a point P1.
(iii) To obtain points systematically draw arcs with centre O and radii O1’, O2’, O3’ etc. intersecting lines O1’, O2’, O3’ etc. at points P1, P2, P3 etc. respectively. In one revolution, P will reach the 12th division along QP and in the next half revolution it will be at the point PQ on the line 18'-0.
(iv) Draw a curve through points P, P1, P2, PQ. This curve is the required Archemedian spiral.
The constant of the curve is equal to the difference between the lengths of any two radii divided by the circular measure of the angle between them.
OP and OP3 (fig. 6-63) are two radii making go0 angle between them. Incircular measure in radian,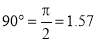
. Therefore, the constant of the curve 
