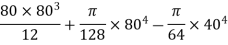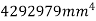Unit 3
Centroid and Moment of Inertia
The center of gravity of any object is termed to the point where gravity acts on the body. Where on the other hand, the centroid is referred to as the geometrical center of a uniform density object. Which means the object has its weight distributed equally across all parts of the body.
- Moment of inertia of rectangular section
Case 1. About X-X axis passing through C.G of the section.
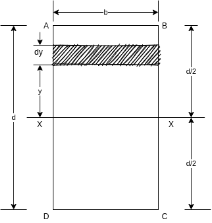
Figure 3 shows rectangular section ABCD having width = b, depth = d. Let X-X is horizontal axis passing through the C.G of rectangular section.
Moment of inertia of given section about X-X axis is represented by 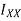
Consider a rectangular elementary strip of thickness dy at a distance y from X -X axis as shown in figure 3.
Area of strip = b.dy
Moment of inertia of area of strip about X-X axis = area of strip 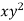
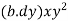
Moment of inertia of whole section will be obtained by integrating the above equation between limits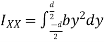
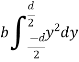
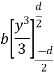
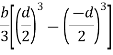
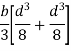
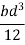
Similarly the moment of inertia of rectangular section about Y-Y axis passing through C.G objection is given by 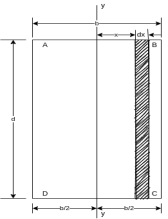
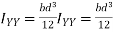
Refer to figure 4.
Proof: self-explanatory
Case 2. Moment of inertia of rectangular section about the line passing through the base.
Consider a rectangular section ABCD having width = b and depth= d. We want to find moment of inertia of section about line CD which is base of rectangular section.
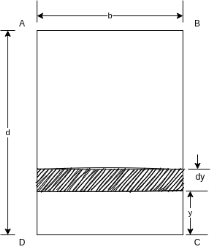
Consider a rectangular elementary strip of thickness dy at a distance y from line CD. As shown in figure 5.
Area of strip = bxdy
Moment of inertia of area of strip About line CD
= Area of strip × 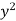
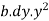
Moment of inertia of whole section about line CD is obtained by integrating the above equation between limits 0 to d.
Moment of inertia of hollow section about line CD
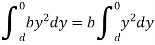
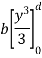
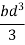
Case 3. Moment of inertia of hollow rectangular section
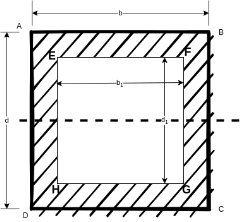
Figure 6 shows a hollow rectangular section in which ABCD is is main section and EFGH is cut out section.
Moment of inertia of main section ABCD about X-X axis is given by
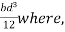
b = width
d = depth of main section
Moment of inertia of cut out section EFGH about X-X axis is given by 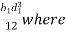
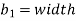
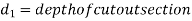
= Moment of inertia of hollow rectangular section about X-X axis
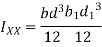
2) Moment of inertia of circular section
Consider a circular section of radius R and centre O. Consider an elementary circular ring of radius r and thickness dr.
Area of circular ring = 2πr.dr
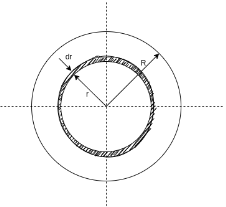
First find moment of inertia of circular section about an Axis passing through O and perpendicular to plane of paper. This moment of inertia is also known as polar moment of inertia.
Let this axis be Z-Z
From theorem of perpendicular axis, the moment of inertia about X-X axis and Y-Y axis is obtained.
Moment of inertia of circular ring about an axis passing through O and perpendicular to plane of paper
= Area of ring × (radius of ring from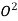
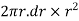
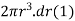
Moment of inertia of hole circular section is obtained by integrating equation 1 between limits O to R.
Moment of inertia of whole section about axis passing through O and perpendicular to plane of paper is given by
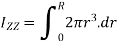
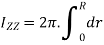
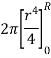
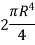
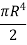
But 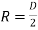
Where D = diameter of circular section
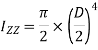
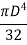
From theorem of perpendicular axis
We have
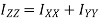
Due to symmetry
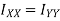
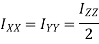
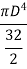
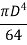
Moment of inertia of hollow circular section
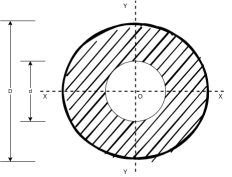
Figure 8 shows hollow circular section
Let D = diameter of outer circle
d = diameter of cut out circle
Moment of inertia of outer circle about X-X axis 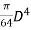
Moment of inertia of cut out circle about X-X axis 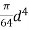
Moment of inertia of hollow circular section about X-X axis
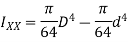
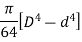
Similarly
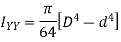
3) Moment of inertia of a triangular section
Case 1. Moment of inertia of triangular section about its base
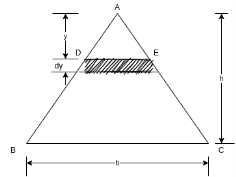
Figure 9 shows triangular section ABC of base b and height h.
Consider a small strip of thickness dy at a distance y from vertex A.
Area of strip = DE × dy
By similarity of ∆ADE and ∆ABC
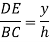
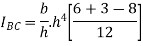
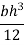
Case 2. Moment of inertia of triangular section about an axis passing through C.G and parallel to base.
Consider a triangular section of base b and height h as shown in figure 10.
Let X-X is axis passing through C.G of triangular section and parallel to base.
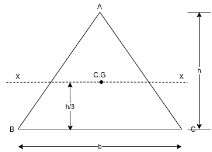
The distance between C.G of triangular section and base AB =h/3
Now from theorem of parallel axis
We have
Moment of inertia about BC = moment of inertia about C.G + area×( distance between X-X and 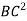
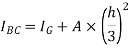
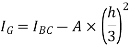
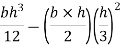
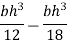
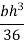
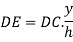
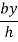
Area of strip 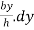
Distance of strip from base = h-y
Moment of inertia of strip about base = area of strip × (distance of strip from bas
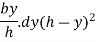
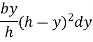
Moment of inertia of whole triangular section about base 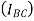 is obtained by integrating above equation between limits 0 to h
is obtained by integrating above equation between limits 0 to h
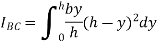
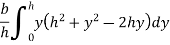
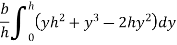
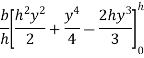
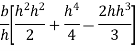
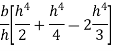
4) Moment of inertia of uniform thin rod
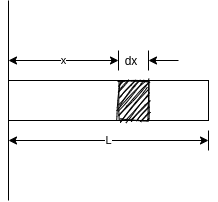
Consider a uniform thin rod AB of length L as shown in figure 11
 Let m = mass per unit length of rod
Let m = mass per unit length of rod
M = total mass of the rod = m×L
Suppose it is required to find M.I. Of rod about Y-Y axis
Consider a strip of length dxx from axis Y-Y
Mass of strip = length of strip× mass per unit length
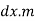
Moment of inertia of strip about Y-Y axis
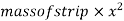
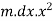
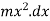
Moment of inertia of hole rod will be obtained by integrating above equation between limits 0 to L.
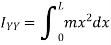
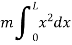
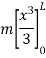
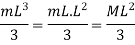
5) Moment of inertia of area under a curve of given equation
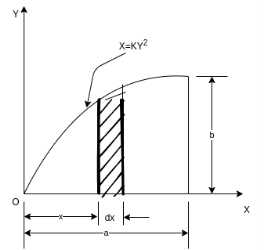
Figure 12 shows an area under a curve whose equation is parabolic and given by
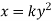
In which, y = b when x =a
To find moment of inertia of this area about y – axis.
Consider a strip of thickness dxx from y axis.
The area of strip dA = y.dx. (1)
Latest substitute values of y in terms of x in above equation
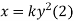
When y = b and x=a
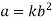
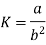
Substituting values of K in equation (2)
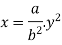
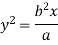
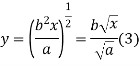
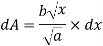
Moment of inertia of elemental area (dA) about y axis
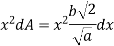
Moment of inertia of total area about y axis is obtained by integrating above equation between limit 0 to a.
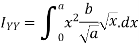
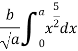
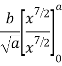
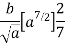
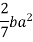
To find moment of inertia of given area about x axis the element shown in figure 12 can be considered to be rectangle of thickness dx. The moment of inertia of this element about X axis is equal to moment of inertia of rectangle about its base
Moment of inertia of element about X axis
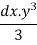
Moment of inertia of given area about x axis is obtained by integrating above equation between limits 0 to a
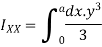
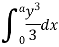
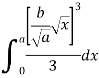
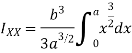
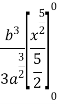
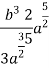
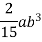
Theorem of perpendicular axis
Theorem of perpendicular axis states that if 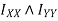 be the moment of inertia of plane section about to two mutually perpendicular axis X-X and Y-Y in the plane of section then moment of inertia of section about the axis Z-Z perpendicular to plane and passing through the intersection of X – X and Y-Y is given by
be the moment of inertia of plane section about to two mutually perpendicular axis X-X and Y-Y in the plane of section then moment of inertia of section about the axis Z-Z perpendicular to plane and passing through the intersection of X – X and Y-Y is given by 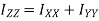
The moment of inertia 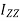 is also known as polar moment of inertia.
is also known as polar moment of inertia.
Proof: a plane section of area A and lying in plane x-y is shown in figure 1.
Let OX and OY be the two mutually perpendicular exist and OZ be perpendicular axis. Consider a small area dA.
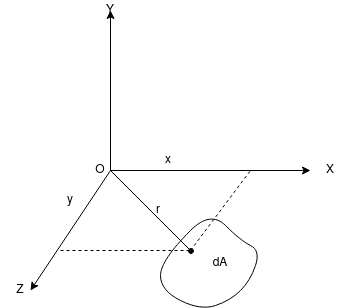
Let x =distance of dA from axis OY.
y = distance of dA from axis OX.
r = distance of dA from axis OZ
Then 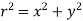
Now, moment of inertia of dA about x-axis
Moment of inertia of total area A about x axis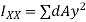
Moment of inertia of total area about y axis 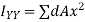
Moment of inertia total area about z – axis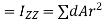
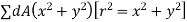
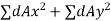
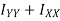
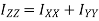
From above equation show that the moment of inertia of an area about an Axis at origin normal to X and Y plane is sum of moment of inertia about corresponding x and y axis.
Theorem of parallel axis
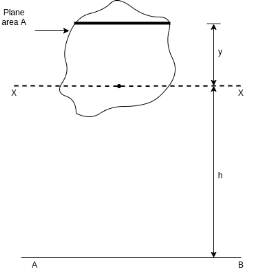
Kids teeth that is moment of inertia of a plane area about an axis plane of area through the CG of the plane area be represented by, then moment of inertia of given plane area about a parallel axis AB of area is given by
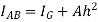
Where
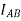 = Moment of inertia of given area about AB
= Moment of inertia of given area about AB
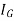 = Moment of inertia of given area about C.G
= Moment of inertia of given area about C.G
A = Area of section
h = distance between the C.G of section and axis AB.
Proof: A lamina of plane area A is shown in figure 2. Let X-X the axis in the plane of area A and passing through C.G of area
AB = axis in plane of area A and parallel to axis X-X.
h = distance between X-X and AB.
Consider a strip parallel to X-X axis at a distance y from the X-X axis
Let, area of the strip =dA
Moment of inertia of area dA about X-X axis =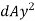
Moment of inertia of the total area about X-X axis =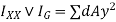
Moment of inertia of the area dA about AB.
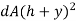
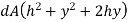
Moment of inertia of total area A about AB
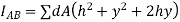
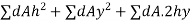
As h is constant
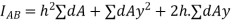
But, 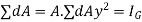
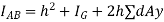
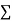 dAy represent the moment of total area about X -X axis. But moments of total area about X-X axis is equal to product of total area A find the distance of C.G total area from X-X axis. As distance of C.G total area from X-X axis is zero.
dAy represent the moment of total area about X -X axis. But moments of total area about X-X axis is equal to product of total area A find the distance of C.G total area from X-X axis. As distance of C.G total area from X-X axis is zero.
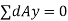
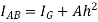
a) First find the location of C.G for given section
b) Then given section is related into rectangles or triangles.
c) Find the moment of inertia of splitted rectangles of triangles about their C.G.
d) Then this moment of inertia is transferred about the axis passing through C.G of given section using theorem of parallel axis.
Radius of gyration of a body about an axis is a distance such that its square multi applied by area gives moment of inertia of area about given axis.
For figure 13 moment of inertia about given axis is given by 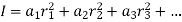
Let whole mass (or area) of body is is concentrated at distance K from axis of reference, then moment of inertia of whole area about given axis will be equal to 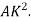
If 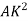 =I then K is known as radius of gyration about a given axis
=I then K is known as radius of gyration about a given axis 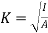
Example 1. 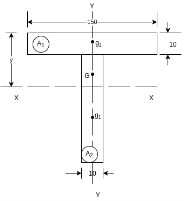 Determine the moment of inertia of section shown in figure 14 about an axis passing through centroid and parallel to top most fibre of section. Also determine moment of inertia about exist of symmetry. Hence find radii of gyration.
Determine the moment of inertia of section shown in figure 14 about an axis passing through centroid and parallel to top most fibre of section. Also determine moment of inertia about exist of symmetry. Hence find radii of gyration.
Solution. Given composite section can be divided into two two rectangles as follows
Area 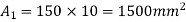
Area 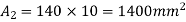
Total area 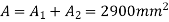
Due to symmetry centroid lies on symmetry axis Y – Y.
The distance of centroid from top most fibre is given by
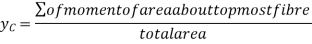
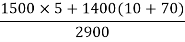
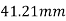
Referring to centroidal axis X-X and y-y then centroid of 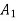 is
is 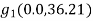 of
of 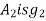
Moment of inertia of section about X-X axis
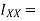 Moment of inertia of
Moment of inertia of 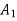 about X-X axis + moment of inertia of
about X-X axis + moment of inertia of 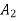 bout X-X axis
bout X-X axis
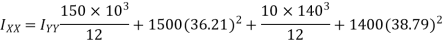
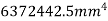
Similarly
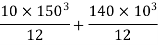
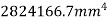
Radius of gyration is given by
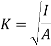
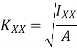
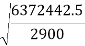
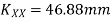
Similarly
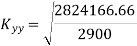
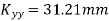
Example 2. Determine moment of inertia of symmetry section shown in figure 15 about its centroidal axis X-X axis and Y-Y axis. Also determine moment of inertia of section about centroidal Axis perpendicular to X-X axis and Y-Y axis.
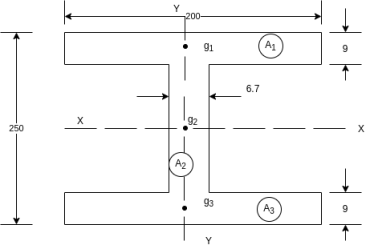
Solution. The section is divided into three rectangles 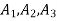
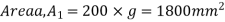
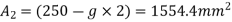
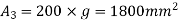
Total area 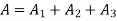
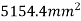
The section is symmetrical about both X-X and Y-Y axis.
Therefore its centroid will coincide with centroid of rectangle 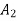
With respect to centroidal axis X-X and Y-Y the centroid of rectangle  and that of
and that of 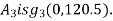
Moment of inertia of 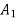 + moment of inertia of
+ moment of inertia of 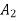 + moment of inertia of
+ moment of inertia of 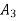 about X – X axis.
about X – X axis.
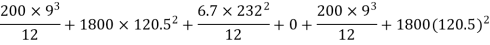
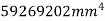
Similarly
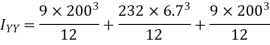
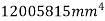
Moment of inertia of section about a centroidal axis perpendicular to X-X and Y-Y axis is nothing but polar moment of inertia and is given by
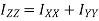
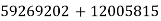
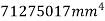
Example 3. Compute the second moment of area of the channel section shown in figure 16 about centroid axis X-X and Y-Y.
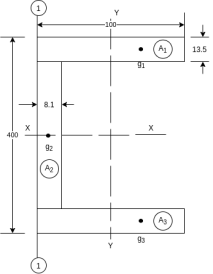
Solution. The section is divided into three rectangles 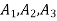
Area 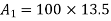
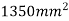
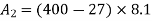
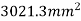
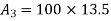
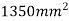
Total area A = 5721.3 
The given section is symmetric about horizontal axis passing through centroid 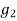 of rectangle
of rectangle 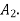 A reference axis (1) –(1) chosen as shown in figure 16.
A reference axis (1) –(1) chosen as shown in figure 16.
The distance of centroid of section from (1)-(1)
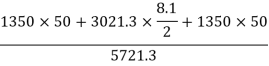
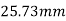
With reference to centroidal axis x-x and y-y then centroid of rectangle 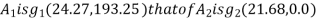 and that of
and that of 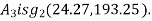
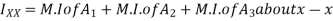
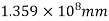
Similarly
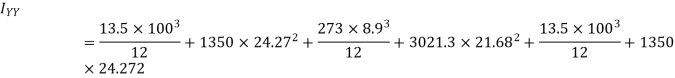
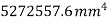
Example 4. Find the moment of inertia of the area shown shaded in figure 17 about edge AB.
Solution. Moment of inertia of shaded portion about AB = moment of inertia of rectangle ABCD about AB - moment of inertia of semicircle on DC about AB.
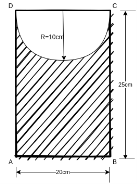
Moment of inertia of rectangle ABCD about AB
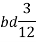
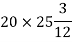
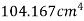
Moment of inertia of semicircle about DC
 × moment of inertia of circle of radius 10cm about a diameter
× moment of inertia of circle of radius 10cm about a diameter
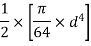
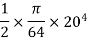
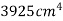
Distance of C.G. Of semi circle from OC
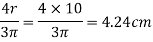
Area of semicircle 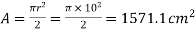
M.I. Of semicircle about line through it C.G parallel to CD
=M.I. Of semicircle about CD =Area 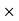 [distance of C.G of semicircle from DC
[distance of C.G of semicircle from DC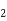
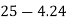
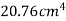
M.I. Of semicircle about AB =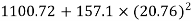
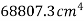
M.I. Of shaded portion about AB
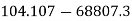
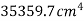
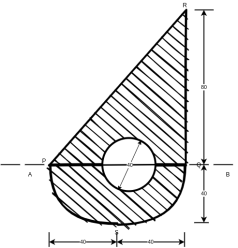
Solution. Given section divided into a triangle PQR a semicircle PSQ having base on axis AB and circle having its centre on axis AB.
Now,
Moment of inertia of the section about axis AB = moment of inertia of triangle PQR about AB + moment of inertia of semicircle PSQ about AB - moment of inertia of circle about AB.