UNIT 3
Entropy
Clausius realized in 1865 that he had discovered a new thermodynamic property and he chose to name this property entropy. It is designated S and is defined as , dS = (dQ / T)
The entropy change of a system during a process can be determined by integrating above Eq. between the initial and the final states

Therefore, the entropy of a substance can be assigned a zero value at some arbitrarily selected reference state, and the entropy values at other states can be determined from above Eq.
∮ dQ / T = 0
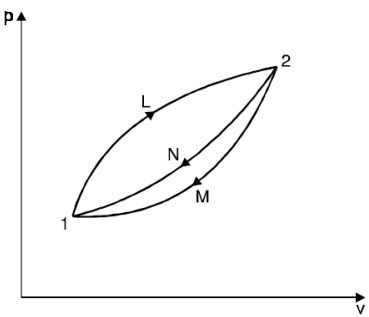

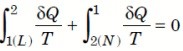
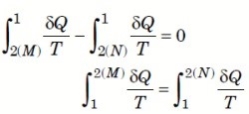
reversible, as shown in Figure.

∮ dQ / T ≤ 0
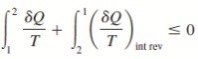
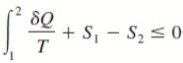
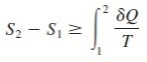
DS ≥ dQ / T
where the equality holds for an internally reversible process and the inequality for an irreversible process.
We may conclude from these equations that the entropy change of a closed system during an irreversible process is greater than the integral of ∂Q/T evaluated for that process.
The inequality sign in the preceding relations is a constant reminder that the entropy change of a closed system during an irreversible process is always greater than the entropy transfer.
That is, some entropy is generated or created during an irreversible process, and this generation is due entirely to the presence of irreversibilities.
The entropy generated during a process is called entropy generation and is
denoted by Sgen.
Noting that the difference between the entropy change of a closed system and the entropy transfer is equal to entropy generation, hence previous Eq. can be rewritten as an equality as
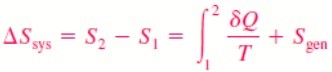
Its value depends on the process, and thus it is not a property of the system. Also, in the absence of any entropy transfer, the entropy change of a system is equal to the entropy generation.
For an isolated system (or simply an adiabatic closed system), the heat transfer is zero
ΔSisolated ≥ 0
This equation can be expressed as the entropy of an isolated system during a process always increases or, in the limiting case of a reversible process, remains constant. In other words, it never decreases. This is known as the increase of entropy principle.
Note that in the absence of any heat transfer, entropy change is due to irreversibilities only, and their effect is always to increase entropy.
The increase of entropy principle can be summarized as

General Case for Change of Entropy of a Gas
Let 1 kg of gas at a pressure p1, volume v1, absolute temperature T1 and entropy s1 be heated such that its final pressure, volume, absolute temperature and entropy are p2, v2, T2 and s2 respectively.
Then by law of conservation of energy,

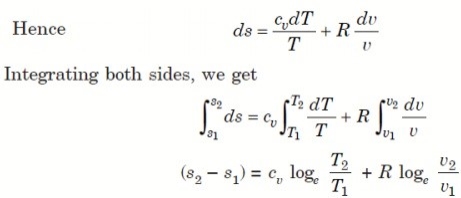
Or we can re-produce
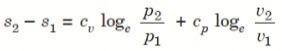
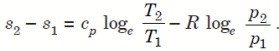
The integral of dQ / T is always less than or equal to zero.
∮ dQ / T ≤ 0
This inequality is valid for all cycles in this universe without any exceptions.
To demonstrate the validity of the Clausius inequality, consider a system connected to a thermal energy reservoir at a constant thermodynamic (i.e., absolute) temperature of TR through a reversible cyclic device.
The cyclic device receives heat ∂QR from the reservoir and supplies heat ∂Q to the system whose temperature at that part of the boundary is T (a variable) while producing work ∂Wrev.
The system produces work ∂Wsys as a result of this heat transfer.
Balancing the combined system identified by dashed lines yield
ΔWc = δQR - dEc
Considering that the cyclic device is a reversible one, we have
δQR / TR = δQ / T
Eliminating ∂QR from the two relations above yields
ΔWc = TR δQ / T - dEc
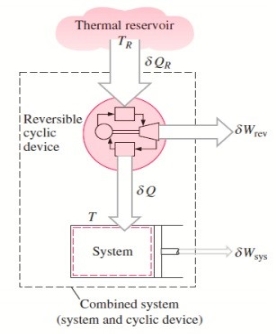
We let the system undergo a cycle while the cyclic device undergoes an integral number of cycles. Then the preceding relation becomes
Wc = TR ∮ dQ / T
Here WC is the cyclic integral of ∂WC, and it represents the net work for the combined cycle.
∮ dQ / T ≤ 0
According to 2nd law of thermodynamics, complete conversion of absorbed heat energy into equivalent amount of work is impossible.
Let us assume energy Q as heat, received from a body having temperature T.
The work done would be maximum if the engine operates on Carnot Cycle. The body at temperature T as source and the atmospheric temperature T0 as the sink.
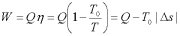
Where Ds is the change in entropy of the body
The Carnot cycle and the available energy is shown in figure.
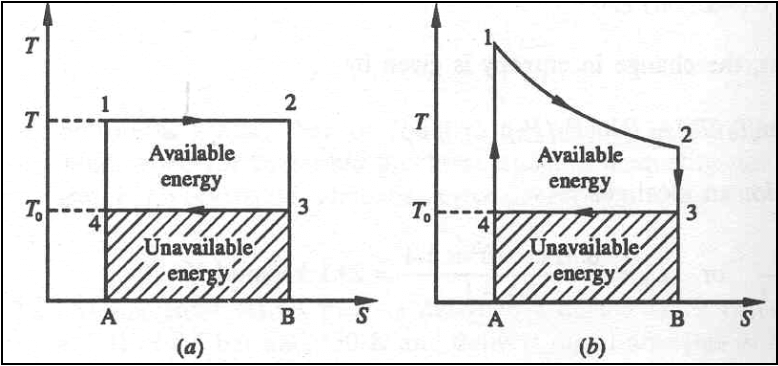
The area 1-2-3-4 represents the amount of energy available for utilization. The shaded are represents unavailable energy.
Availability Function for Non-Flow process:
If P0 is atmospheric pressure, V1 and V0 are the initial and final volumes of the system respectively.
If the system comes to equilibrium with its surroundings, the work done in against the atmospheric pressure is P0(V0-V1).
Availability = Wuseful = Wmax - P0(V0-V1)
Wmax=(U1-U0) - T0 (S1-S0)
Availability = Wuseful = Wmax-P0(V0-V1)
= (U1 - T0 S1)- (U0 - T0 S0)- P0(V0-V1)
= (U1 + P0V1 - T0 S1) - (U0 + P0V0 - T0 S0)
= f1-f0
Where, f = U+P0V-T0S is availability function for the non-flow process. Thus, the availability: f1 - f0
Availability Function for Steady Flow process:
The maximum work that can be done in a SF process while the control volume exchanges heat with the atmosphere at T0, is given by:
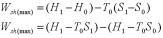
It can also be expressed as
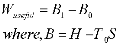
which is called the Darrieus Function.