UNIT 2
Ideal Gas and Second law of Thermodynamics
An ideal gas has no intermolecular interaction and its molecules occupy very negligible space.
No gas in the universe is perfectly ideal.
But all gases approach ideal conditions as temperature approaches absolute zero.
Ideal gas follows all the gas laws that are stated below:
P ∝ 1/ V or PV = k
2. Charles' law: (at P = const)
V ∝ T or V/T = k
3. Gay-Lussac's law: (at V = const)
P ∝ T or P/T = k
4. Avogadro's law: Avogadro's law states that, "equal volumes of all gases, at the same temperature and pressure, have the same number of molecules”
V ∝ n or V/n = k
Where, n is the amount of substance of the gas (measured in moles).
An imaginary gas which obeys this law pv = R*T = constant, at all Pressure and Temperature is called an ideal gas, and the equation is called Characteristic equation of state for ideal gas.
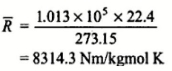
This R* is called universal gas constant.
Also, specific volume, v = V / n,
V = total volume and n = number of moles.
∴ pV = n R*T
But, n = m/M, where M – is Molecular weight
∴ pV = mR*T / M
∴ pV = mRT
Where, R*/ M = R = Characteristic gas constant
The Value of “R” will depend upon particular gas and can be found
using R* = 8314.3 J/mol K and M – molecular weight of gas.
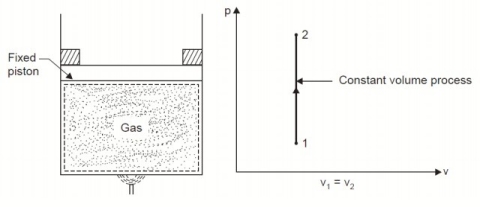
Considering mass of the working substance unity and applying first law of thermodynamics to the process,

2. Constant Pressure or Isobaric Process:
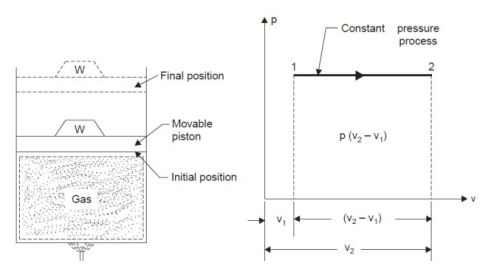
Considering unit mass of working substance and applying first law of thermodynamics to the process,
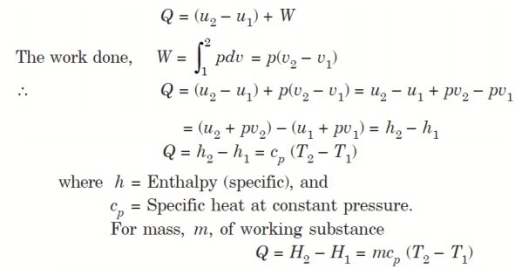
3. Constant Temperature or Isothermal Process:
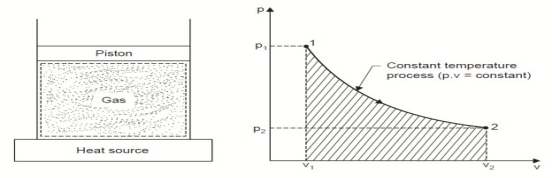
Considering unit mass of working substance and applying first law to the process,
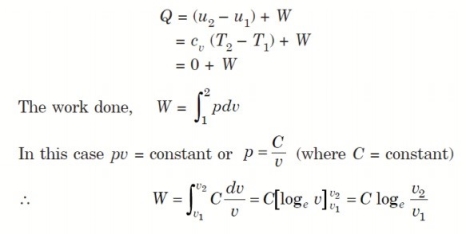
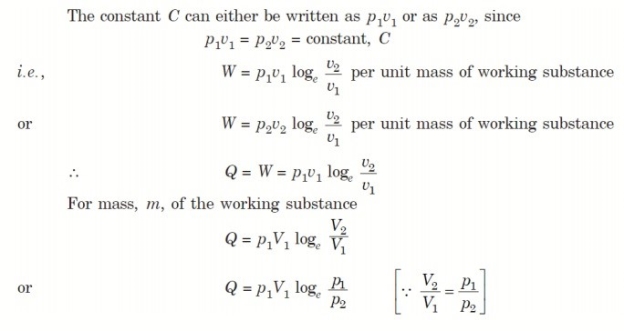
4. Reversible Adiabatic Process (PV γ = constant)
An adiabatic process is one in which no heat is transferred to or from the fluid during the process. Such a process can be reversible or irreversible.
Considering unit mass of working substance and applying first law to the process
Q = (u2 – u1) + W
O = (u2 – u1) + W
or W = (u1 – u2) for any adiabatic process
Above equation is true for an adiabatic process whether process is reversible or not.


5. Throttling Process (Isenthalpic Process)
It is a process in which the enthalpy of the system remains constant. During this process, no work is done and usually heat transfer between system and surroundings is also zero. It is an irreversible process.
A body that is an infinite supply of heat energy is called as thermal reservoir.
The temperature of such a body is not affected by addition or removal of enormous amount of heat.
It is an engine that absorbs heat from a hotter body and transfers it to a colder body and produces maximum work without any losses.
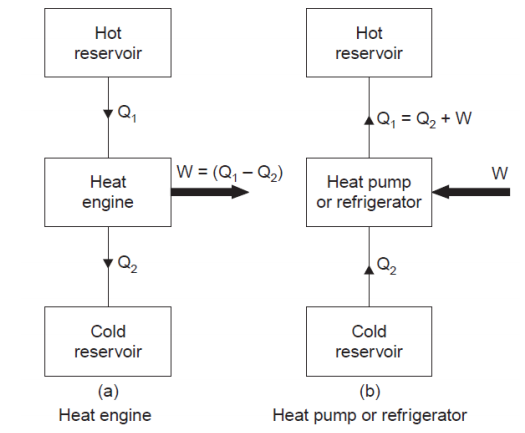
The efficiency of heat engine is given by hth = W / Q1
Where, W = work produced by the engine.
Q1 = heat absorbed from the hot body
Heat pump is heat engine in reversed direction.
The purpose of heat pump is to deliver heat Q1 to the hotter body at the expense of work W.
For reversed heat engines, the concept of efficiency does not exist.
Rather the measure of success is done by Coefficient of Performance.
Coefficient of Performance = Q1 / W
Refrigerator is same as heat pump.
The purpose of refrigerator is to extract heat Q2 to the colder body at the expense of work W.
The measure of success is done by Coefficient of Performance.
Coefficient of Performance = Q2 / W
The second law of thermodynamics has two statements put forward by two scientists.
Although the Clausius and Kelvin-Planck statements appear to be different, they are really equivalent in the sense that a violation of either statement implies violation of other.
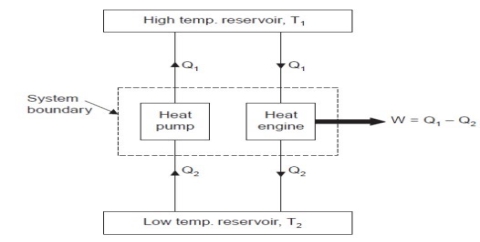
Consider a hotter body at temperature T1 and colder body at temperature T2.
Fig. shows a heat pump that transfers heat Q2 from colder body to hotter body without any external work. This violates the Clausius statement.
Let an amount of heat Q1 (greater than Q2) be transferred from hotter body to heat engine which produces work, W = Q1 – Q2 and rejects Q2 to the colder body.
Since there is no heat interaction with the colder body, it is neglected. This combined system of engine and pump are acting like an heat engine exchanging heat with a single reservoir, which violates the Kelvin-Planck statement.
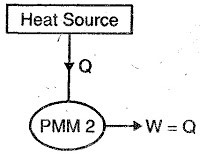
This machine violates the second law of thermodynamics because such machines will absorb heat energy continuously from a thermal reservoir and will convert the absorbed heat energy completely in to equivalent amount of work.
This machine will have efficiency 100%, or we can say that perpetual motion machines of second kind will have higher efficiency than ideal Carnot cycle and it is not possible.
Therefore, we can say that perpetual motion machine of second kind will also does not exist as such machines violate the second law of thermodynamics.
Figure showing below a graphical representation of PMM2
The integral of dQ / T is always less than or equal to zero.
∮ dQ / T ≤ 0
This inequality is valid for all cycles in this universe without any exceptions.
The cyclic device receives heat ∂QR from the reservoir and supplies heat ∂Q to the system whose temperature at that part of the boundary is T (a variable) while producing work ∂Wrev.
The system produces work ∂Wsys as a result of this heat transfer.
Balancing the combined system identified by dashed lines yield
ΔWc = δQR - dEc
Considering that the cyclic device is a reversible one, we have
δQR / TR = δQ / T
Eliminating ∂QR from the two relations above yields
ΔWc = TR δQ / T - dEc
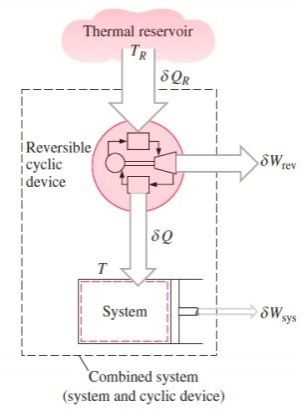
We let the system undergo a cycle while the cyclic device undergoes an integral number of cycles. Then the preceding relation becomes
Wc = TR ∮ dQ / T
Here WC is the cyclic integral of ∂WC, and it represents the net work for the combined cycle.
∮ dQ / T ≤ 0
A reversible process should fulfil the following conditions:
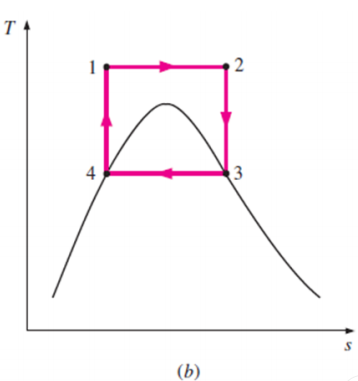
The Carnot cycle is the most efficient cycle operating between two specified temperature limits. Thus, it is natural to look at the Carnot cycle first as a prospective ideal cycle for vapor power plants.
However, the Carnot cycle is not a suitable model for power cycles.
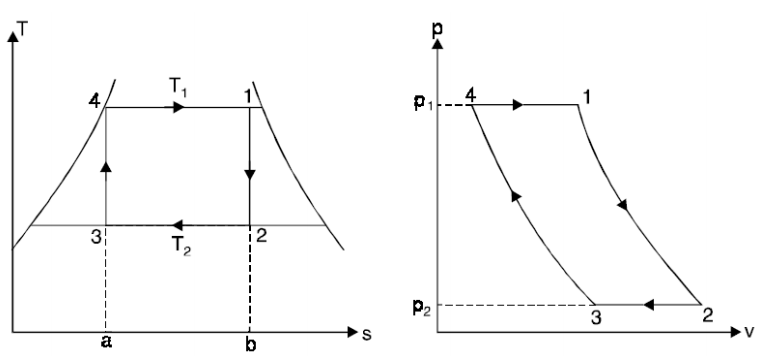
Thus cycle is completed.
Net work done = Heat supplied – heat rejected
= T1 (s2 - s3) - T2 (s2 - s3)
= (T1 – T2) (s2 - s3)
Carnot Efficiency η = Work done / Heat supplied = (T1 – T2) (s2 - s3) / T1 (s2 - s3)
= (T1 – T2) / T1
Limitations or Impracticalities of Carnot Cycle:
Though Carnot cycle is simple (thermodynamically) and has the highest thermal efficiency for given values of T1 and T2, still it is impossible to produce in actuality because:
Some of these problems could be eliminated by executing the Carnot cycle in a different way, as shown in Fig. B.