Unit-1

Linear differential equations

1.1 LDE of nth order with constant coefficient

A homogeneous linear ordinary differential equation with constant coefficients is an ordinary differential equation in which coefficients are constants, all terms are linear, and the entire differential equation is equal to zero,

The form of second-order linear differential equation with constant coefficients is,

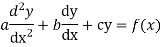
Where a,b,c are the constants.

 Let, aD²y+bDy+cy = f(x),    where d² = 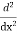,  D =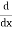

∅(D)y = f(x)   , where ∅(D)y = aD²y+bDy+cy

Here first we solve,  ∅(D)y = 0, which is called  complementary function(C.F)

Then we find particular integral (P.I)

P.I. = 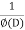f(x)

General solution = C.F. +P.I.

Linear differential equations are those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.

Thus the general linear differential equation of the nth order is of the form

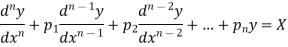
Where 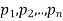and X isa function of x.

Linear differential equation with constant coefficient is of the form-

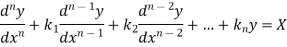
Where 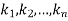are constants.

Let’s do some examples to understand the concept,

Example1: Solve (4D² +4D -3)y =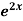 

Solution: Auxiliary equation is 4m² +4m – 3 = 0

    We get,             (2m+3)(2m – 1) = 0

m =   ,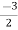

complementary function:  CF is  A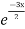+ B

now we will find particular integral,

P.I. = 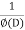f(x)

=   .

=    .

=    .

=   . =   .

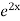
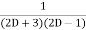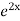
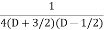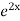
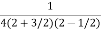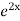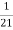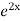
 General solution is y =  CF + PI

= A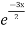+ B  .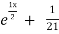

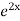
Differential operators

D stands for operation of differential i.e.

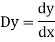
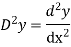
stands for the operator of integration.

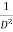stands for operation of integration twice.

Thus,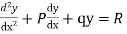

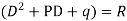
Note:-Complete solution = complementary function + Particular integral

i.e. y=CF + PI

Rules to find the complementary function-

To solve the equation-

This can be written as in symbolic form-

Or-
 

It is called the auxiliary equation.

Let 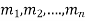be the roots-

Case-1: If all the roots are real and distinct, then equation (2) becomes,

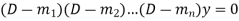
Now this equation will be satisfied by the solution of

This is a Leibnitz’s linear and I.F. =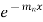

Its solution is-

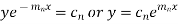
The complete solution will be-

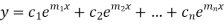
Case-2: If two roots are equal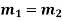

Then the complete solution is given by-

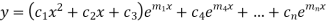
Case-3: If one pair of roots be imaginary, i.e. then the complete solution is-

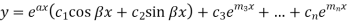
Where and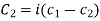

Case-4: If two points of imaginary roots are equal-

Then the complete solution is-

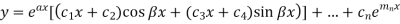
Example-Solve

Sol.

Its auxiliary equation is-

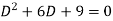
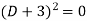
Where-

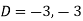
Therefore the complete solution is-

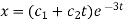
Example: Solve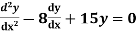

Ans. Given,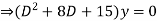

Here the Auxiliary equation is

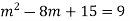
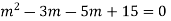
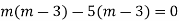
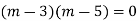
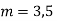
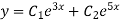
Example: Solve

Or,

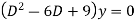
Ans. Auxiliary equation is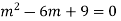

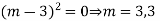
Note: If roots are in complex form i.e.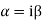

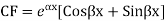
Example:  Solve

Ans. Auxiliary equation is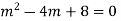

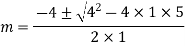
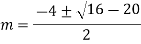
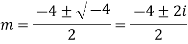
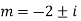
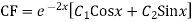
Rules to find Particular Integral

Case 1: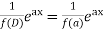

If,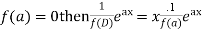

If,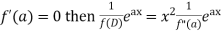

Example:Solve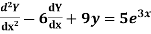

Ans. Given,

Auxiliary equation is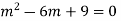

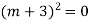
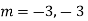
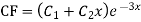
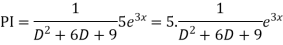
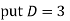
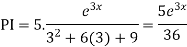
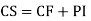
Case2: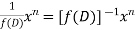

Expand 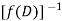by the binomial theorem in ascending powers of D as far as the result of an operation on 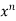is zero.

Example.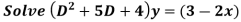

Given,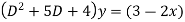

For CF,

Auxiliary equation is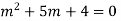

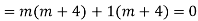
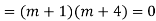
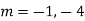
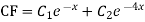
For PI

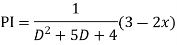
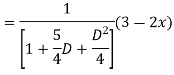
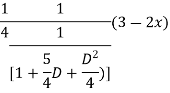
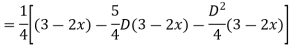
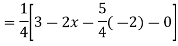
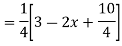
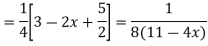
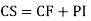
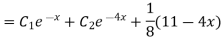
Case 3:

Or,

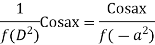
Example: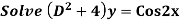

Ans. Auxiliary equation is

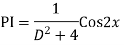
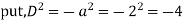
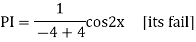
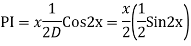
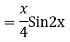
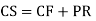
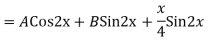
Case 4: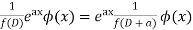

Example: Solve

Ans. AE=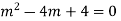

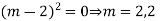
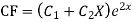
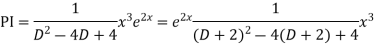
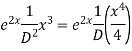
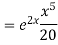
The complete solution is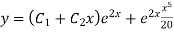

Example: Solve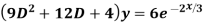

Ans. The AE is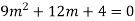

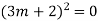
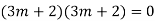
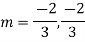
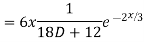
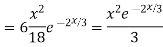
Complete solution y= CF + PI

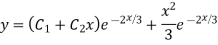
Example: Solve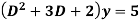

Ans. The AE is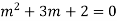

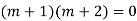
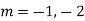
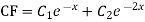
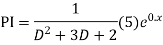
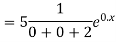
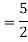
Complete solution = CF + PI

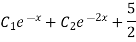
Example:  Solve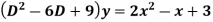

Ans. The AE is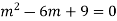

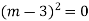
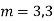
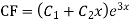
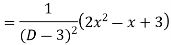
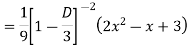
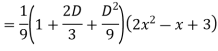
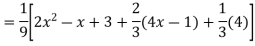
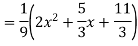
Complete solutio0n is y= CF + PI

Example: Find the PI of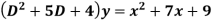

Ans.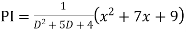

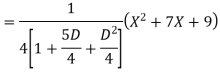
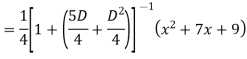
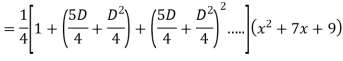
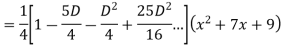
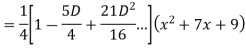
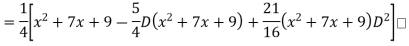
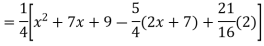
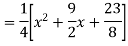
Example: solve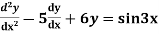

Ans. Given equation in symbolic form is

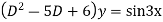
Its Auxiliary equation is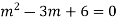

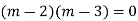
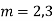
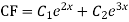
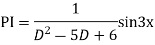
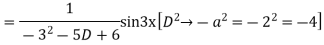
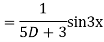
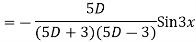
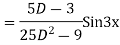
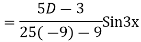
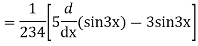
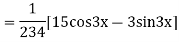
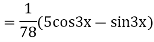
Complete solution is y= CF + PI

Example:  Solve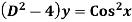

Ans. The AE is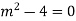

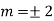
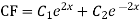
We know,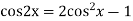

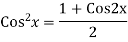
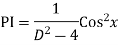
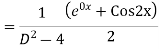
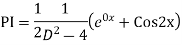
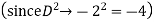
Complete solution is y= CF + PI

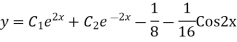
Example: Find the PI  of(D2-4D+3)y=ex cos2x

Ans.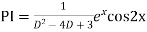

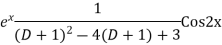
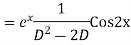
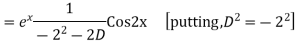
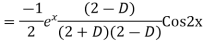
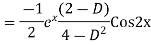
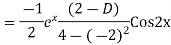
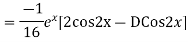
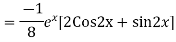
Example.  Solve(D3-7D-6) y=e2x (1+x)

 Ans. The auxiliary equation i9s

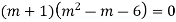
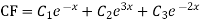
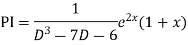
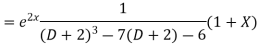
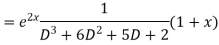
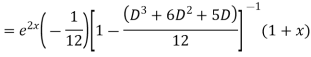
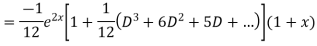
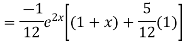
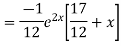
Hence complete solution is y= CF + PI

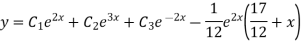
Key takeaways-

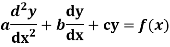
2.     General solution = C.F. +P.I.

3.     If all the roots are real and distinct, then

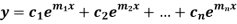
4.     If two roots are equal then

5.     If one pair of roots be imaginary, i.e. 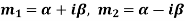then the complete solution is-

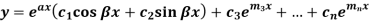
6.     If two points of imaginary roots are equal-

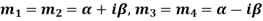
Then the complete solution is-

1.2 The general method and Short methods

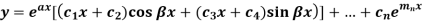
A general method of finding the PI of any function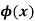

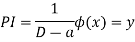
Or

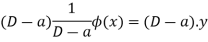
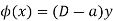
Or

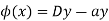
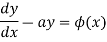
It is the LDE.

The solution will be-

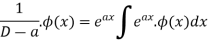
Example:

Solve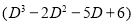

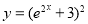
Solution:

Auxiliary equation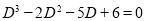  

Complementary function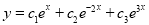

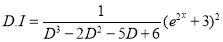
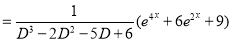
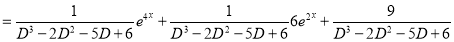
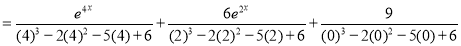
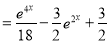
Complete Solution is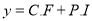  

Example:

Solve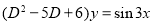

Solution:

Auxiliary equation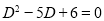

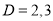
C.F is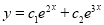

  []

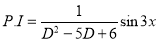
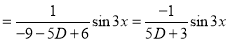
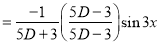
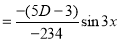
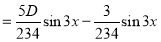
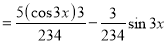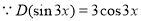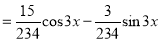
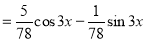
   The Complete Solution is  

Example

Solve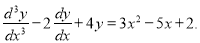 

Solution:

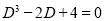
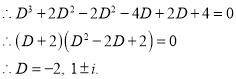
The Auxiliary equation is

  The C.F is  

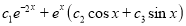
P.I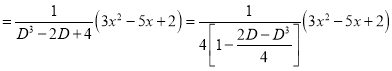

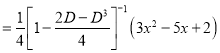
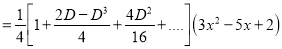
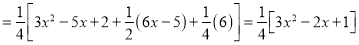
   The Complete Solution is 

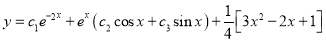
Example

Solve

Solution:

The Auxiliary equation is   

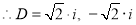
  The C.F is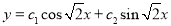

P.I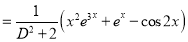

Now,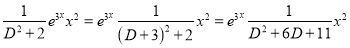  

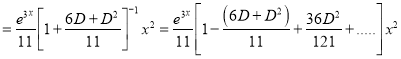
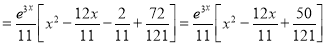
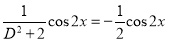
  The Complete Solution is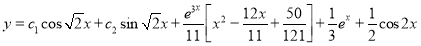

Example

Solve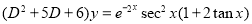

Solution:

The auxiliary equation is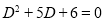

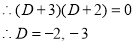
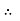The C.F is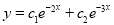

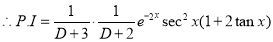
 [Put ]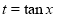

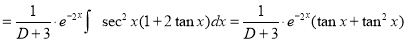
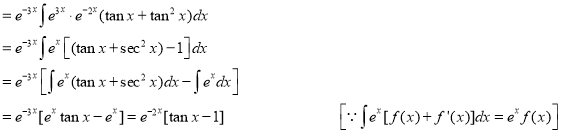
   The Complete Solution is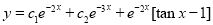

Example

Solve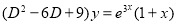

Solution:

The auxiliary equation is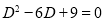     

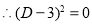
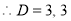
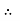The C.F is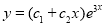

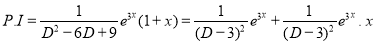
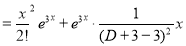
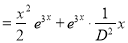
But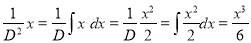

   The Complete Solution is

Example

Solve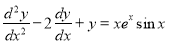

Solution:

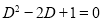
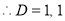
The auxiliary equation is   

The C.F is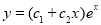

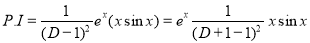
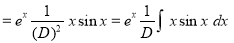
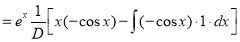 [By parts]

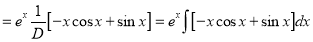
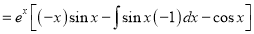
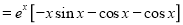
   The Complete Solution is

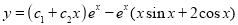
Example

Solve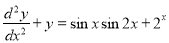

Solution:

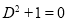
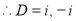
The auxiliary equation is 

The C.F is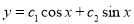

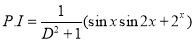
Now,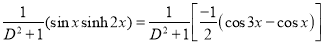 

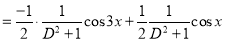
And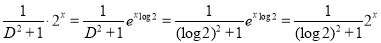 

   The Complete Solution

1.3 Methods of variation of parameters

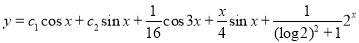
Consider a second-order LDE with constant coefficients given by

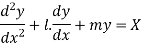
Then let the complimentary function 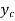is given by

Then the particular integral is

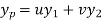
Where u and v are unknown and to be calculated using the formula

u=

Example-1: Solve the following DE by using a variation of parameters-

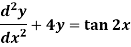
Sol. We can write the given equation in symbolic form as-

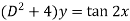
To find CF-

It’s A.E. is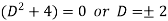

So that CF is-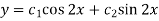     

To find PI-

Here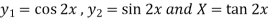

Now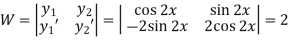

Thus PI = 

            = 

            = 

             = 

             = 

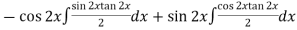
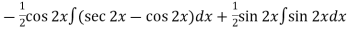
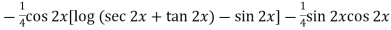
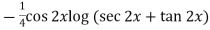
So that the complete solution is-

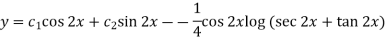
Example-2: Solve the following by using the method of variation of parameters.

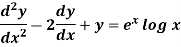
Sol. This can be written as-

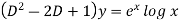
C.F.-

The auxiliary equation is-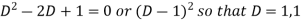

So that the C.F. will be-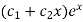

P.I.-

Here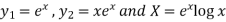

Now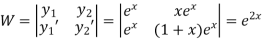

Thus PI =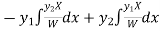 

            = 

            = 

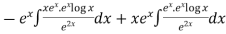
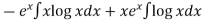
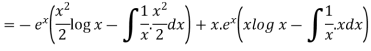
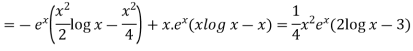
So that the complete solution is-

1.4 Cauchy’s and Legendre’s Different1ial Equation

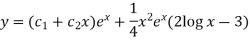
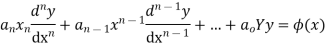
Where, 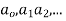are constant is called Cauchy’s homogenous linear equation.

Put,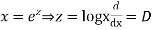

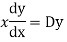
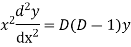
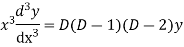
Example.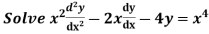

Ans. Putting,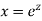

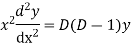
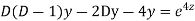
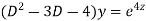
AE is

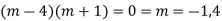
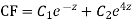
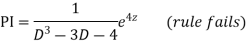
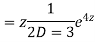
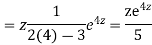
CS = CF + PI

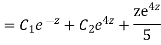
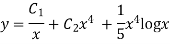
Example: Solve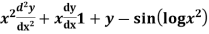

Ans. Let,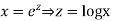

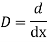
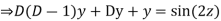
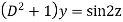
AE is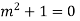

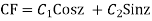
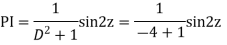
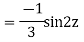
y= CF + PI

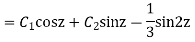
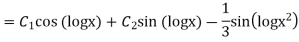
Example: Solve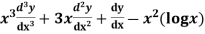

Ans. Let, 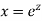so that z = log x

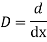
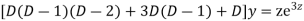
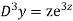
AE is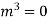

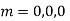
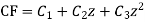
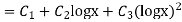
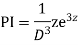
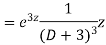
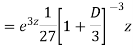
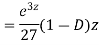
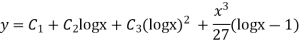
Legendre’s differential equation-

A differential equation of the form-

Where k is the constants and X is a function of x, is known as Legendre’s linear differential equation.

We can reduce such type of equations to linear equations with constant coefficient by the substitution as-

i.e.

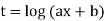
Example: Solve

Sol. As we see that this is Legendre’s linear equation.

Now put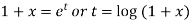

So that-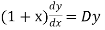

And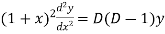

Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t

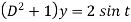
Its auxiliary equation is-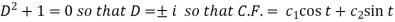

And particular integral-

               P.I. =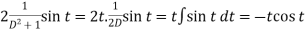

Note -

Hence the solution is -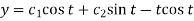

Key takeaways-

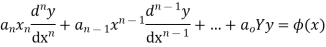
2.     Legendre’s linear differential equation-

1.5 Simultaneous and symmetric simultaneous differential equations

The equation involving the derivatives of two or more dependent variables, which are the functions of a single independent variable, is called a simultaneous equation.

Such as-

Example 1: Solve the following simultaneous differential equations-

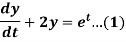
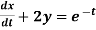....(2)

Solution:

Consider the given equations

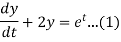
....(2)

Consider eq(1),(2)

 Dx+2y = et....(1)

Dx +2x =e-t....(2)

Eliminating ‘x’ from both the equations we get,

12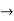 2Dx + 2y = 2et

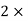D 2Dx +D2y = e-t

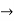y = Ae2t + Be-2t +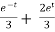

Example 2: Solve the following simultaneous differential equations-

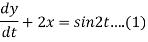
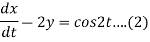
Given that x(0)=1  and y(0)= 0

Solution:

Consider the given equations,

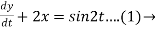Dy +2x = sin2t

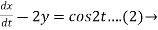Dx -2y = cos2t

By solving the above equations we get,

(D2 +4)Y =0

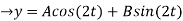
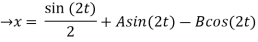
X(0) = 1, y(0) = 0

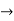A =0, B=-1

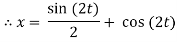
Example-3: Solve the following simultaneous differential equations-

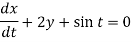
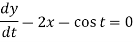
It is given that x = 0 and y = 1 when t = 0.

Sol. Given equations can be written as-

Dx + 2y = - sin t ………. (1)    and     -2x + Dy = cos t  ……… (2)

Eliminate x by multiplying (1) by 2 and (2) by D then add-

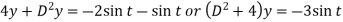
Here A.E =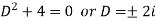

So that C.F. =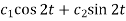

And P.I. =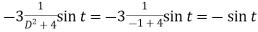

So that- 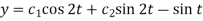   …………. (3)

And 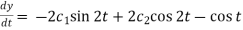  ………….. (4)

Substitute (3) in (2), we get-

 2x = Dy – cos t =

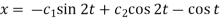  ………… (5)

When t = 0, x = 0, y = 1. (3) and (5) gives-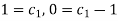 

Hence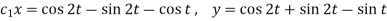

References

1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.

2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.

3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers