Unit - 2
Orthogonal Frequency Division Multiplexing
Orthogonal frequency division multiplexing can accommodate high data rate in the mobile wireless systems in order to handle multimedia services. It is important to understand the OFDM technology because the channel estimation is an integral part of OFDM system. OFDM technology can be used effectively to avoid the effect of frequency-selective fading and narrowband interference from parallel closely spaced frequencies in mobile networks. If there is no orthogonality in the channel, inter-channel interference (ICI) can be experienced. With these vital advantages, OFDM technology has been widely used by many wireless standards such as WLAN, WMAN, and DVB. In OFDM scheme, complex filters are not required and time-spreading can be used without any complications in OFDM scheme.
OFDM scheme can also help to manage the single frequency networks (SFN) by sending the same signals at the same frequency using adjacent transmitters without interfering each other. OFDM has been popularly used for various wireless communication systems such as fourth generation 4G wireless system. Since we want to test and evaluate the use of Digital Prolate Spheroidal Sequences based on OFDM technology, we give a brief introduction to OFDM system. Orthogonal frequency-division multiplexing (OFDM) is based on the frequency division multiplexing (FDM) scheme used as digital multi-carrier modulation method, particularly in estimating a channel in two-dimensions (time – frequency lattice). The technology is intended for downlink in the physical layer. The OFDM channel is divided into several narrowband sub-carriers and designed to be orthogonal with each other in the frequency domain for carrying data symbols.
Each sub-carrier has parallel narrow band-pass channels at low symbol rate. The advantage of using a low symbol rate is that it is possible to use a guard interval between symbols and to avoid the inter-symbol interference. In the OFDM the total data rate for sub-carriers are equivalent to the single carrier modulation with the same bandwidth. The OFDM plays an important role in the wideband of mobile wireless systems.
Advantages of OFDM
The OFDM methods can help the mobile wireless channel transmit large amounts of data through the mobile channel. The carrier of the OFDM has a low bit rate data stream, which enables the system to have high data rate, high data capacity, as well as eliminating the intersymbol interference (ISI) in the system. The OFDM technology uses the efficient Fast Fourier Transform algorithm which reduces complexity of modulation/demodulation process. OFDM is less sensitivity to the error caused by time synchronization of the network. OFDM technology works well because it can avoid and eliminate the inter-symbol interference (ISI) as well as the fading caused by multipath propagation.
The disadvantage of the OFDM
The technology is very sensitive to the Doppler shift that is very common in mobile wireless communication systems. OFDM is very sensitive to frequency synchronization errors. Moreover, the overall efficiency reduces by inserting cyclic prefix /guard interval.
- The Orthogonal Frequency Division Multiplexing (OFDM) transmission scheme is the optimum version of the multicarrier transmission scheme. In the past, as well as in the present, the OFDM is referred in the literature Multi-carrier, Multi-tone and Fourier Transform.
- In mid-1960 parallel data transmission and frequency multiplexing came. In high-speed digital communication OFMD is employed. OFMD has a drawback of massive complex computation and high-speed memory which are no more problems now due to introduction of DSP and VLSI.
- The implementation of this technology is cost effective as FFT eliminates array of sinusoidal generators and coherent demodulation required in parallel data systems· The data to be transmitted is spread over large number of carriers. Each of them is then modulated at low rates. By choosing proper frequency between them the carriers are made orthogonal to each other.
- In OFDM the spectral overlapping among the sun carrier is allowed, at the receiver due to orthogonality the subcarriers can be separated. This provides better spectral efficiency and use to steep BPF is eliminated.
- The problems arising in single carrier scheme are eliminated in OFDM transmission system. It has the advantage of spreading out a frequency selective fade over many symbols. This effectively randomizes burst errors caused by fading or impulse interference so that instead of several adjacent symbols being completely destroyed, many symbols are only slightly distorted.
- Because of this reconstruction of majority of them even without forward error correction is possible. As the entire bandwidth is divided into many narrow bandwidths, the sub and become smaller than the coherent bandwidth of the channel which makes the frequency response over individual sub bands is relatively flat. Hence, equalization becomes much easier than in single carrier system and it can be avoided altogether if differential encoding is employed.
- The orthogonality of sub channels in OFDM can be maintained and individual subchannels can be completely separated by the FFT at the receiver when there are no inter symbol interference (ISI) and intercarrier interference (ICI) introduced by the transmission channel distortion.
- Since the spectra of an OFDM signal is not strictly band limited, linear distortions such as multipath propagation causes each subchannel to spread energy into the adjacent channels and consequently cause ISI.
- One way to prevent ISI is to create a cyclically extended guard interval, where each OFDM symbol is preceded by a periodic extension of the signal itself. When the guard interval is longer than the channel impulse response or multipath delay, the ISI can be eliminated.
- By using time and frequency diversity, OFDM provides a means to transmit data in a frequency selective channel. However, it does not suppress fading itself. Depending on their position in the frequency domain, individual subchannels could be affected by fading.
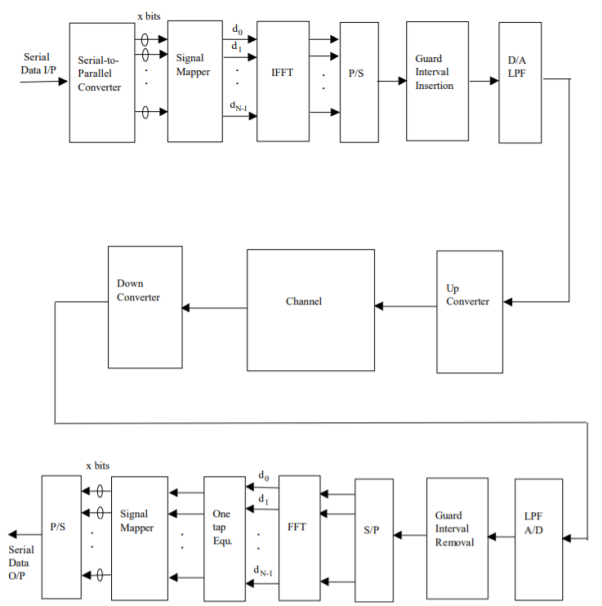
Fig 1: General OFDM System
The incoming signal is converted to parallel form by serial to parallel converter. After that it is grouped in x bits to form a complex number. These numbers are then modulated in a baseband manner by IFFT. Then through parallel to serial converted they are converted to serial data and transmitted. In order to avoid inter symbol interference a guard interval is inserted between the symbols. The discrete symbols are converted to analog and lowpass filtered for RF up-conversion. The receiver performs the inverse process of the transmitter. One tap equalizer is used to correct channel distortion. The tap coefficients of the filter are calculated based on channel information.
Key takeaway
The OFDM scheme differs from traditional FDM in the following interrelated ways:
- Multiple carriers (called subcarriers) carry the information stream
- The subcarriers are orthogonal to each other.
- A guard interval is added to each symbol to minimize the channel delay spread and inter-symbol interference.
The OFDM technology is widely used in two types of working environments, i.e., a wired environment and a wireless environment. When used to transmit signals through wires like twisted wire pairs and coaxial cables, it is usually called as DMT (digital multi-tone). For instance, DMT is the core technology for all the xDSL (digital subscriber lines) systems which provide high-speed data service via existing telephone networks. However, in a wireless environment such as radio broadcasting system and WLAN (wireless local area network), it is referred to as OFDM. Since we aim at performance enhancement for wireless communication systems, we use the term OFDM throughout this thesis. Furthermore, we only use the term MIMO-OFDM while explicitly addressing the OFDM systems combined with multiple antennas at both ends of a wireless link.
The history of OFDM can all the way date back to the mid 1960s, when a paper on the synthesis of bandlimited orthogonal signals for multichannel data transmission. He presented a new principle of transmitting signals simultaneously over a bandlimited channel without the ICI and the ISI. Right after Chang’s publication of his paper, Saltzburg demonstrated the performance of the efficient parallel data transmission systems in 1967, where he concluded that “the strategy of designing an efficient parallel system should concentrate on reducing crosstalk between adjacent channels than on perfecting the individual channels themselves”. His conclusion has been proven far-sighted today in the digital baseband signal processing to battle the ICI.
Through the developments of OFDM technology, there are two remarkable contributions to OFDM which transform the original “analog” multicarrier system to today’s digitally implemented OFDM. The use of DFT (discrete Fourier transform) to perform baseband modulation and demodulation was the first milestone when Weinstein and Ebert published their paper in 1971. Their method eliminated the banks of subcarrier oscillators and coherent demodulators required by frequency-division multiplexing and hence reduced the cost of OFDM systems. Moreover, DFT-based frequency-division multiplexing can be completely implemented in digital baseband, not by bandpass filtering, for highly efficient processing. FFT, a fast algorithm for computing DFT, can further reduce the number of arithmetic operations from N2 to NlogN (N is FFT size).
Recent advances in VLSI (very large scale integration) technology has made high-speed, large-size FFT chips commercially available. They used a guard interval between consecutive symbols and the raised-cosine windowing in the time-domain to combat the ISI and the ICI. But their system could not keep perfect orthogonality between subcarriers over a time dispersive channel. This problem was first tackled by Peled and Ruiz in 1980 with the introduction of CP (cyclic prefix) or cyclic extension. They creatively filled the empty guard interval with a cyclic extension of the OFDM symbol.
If the length of CP is longer than the impulse response of the channel, the ISI can be eliminated completely. Furthermore, this effectively simulates a channel performing cyclic convolution which implies orthogonality between subcarriers over a time dispersive channel. Though this introduces an energy loss proportional to the length of CP when the CP part in the received signal is removed, the zero ICI generally pays the loss. And it is the second major contribution to OFDM systems. With OFDM systems getting more popular applications, the requirements for a better performance have been becoming higher. Hence more research efforts are poured into the investigation of OFDM systems.
Pulse shaping , at an interference point view, is beneficial for OFDM systems since the spectrum of an OFDM signal can be shaped to be more well-localized in frequency; Synchronization in time domain and in frequency domain renders OFDM systems robust against timing errors, phase noise, sampling frequency errors and carrier frequency offsets; For coherent detection, channel estimation provides accurate channel state information to enhance performance of OFDM systems; Various effective techniques are exploited to reduce the relatively high PAPR such as clipping and peak windowing.
Bit Error Rate
Capacity is maximum possible information that can be transmitted with available bandwidth and transmitted power. In single antenna SISO having bandwidth B, transmitted power P, noise spectrum No and channel assumed to be white Gaussian, then the capacity of a system is given by Shannon’s capacity formula
C=B log2 (1+SNR)
When multiple antennas are used, channel faces multiple input and output, and its capacity is determined by extended Shannon’s capacity. Antenna with Nt input from transmitter and Nr output in a receiver channel is expressed as Nr * Nt matrix of channel H The capacity of a MIMO channel can be estimated by the following equation
C = log2 det (I +  )
)
Where H is Nr x Nt channel matrix, Rx is covariance of input signal x, HH is transpose conjugate of H matrix and is the variance of the uncorrelated and Gaussian noise [16]. Since this equation is obtained by large theoretical calculations, but practically it has never been achieved yet. To achieve more precise results linear transformation at both transmitter and receiver can be performed by converting MIMO channel (Nr, Nt) to a SISO sub channel min (Nr, Nt). According to singular value decomposition (SVD) every matrix can be decomposed. Suppose the channel matrix H transformation is given by H = UDVH, Where the matrix U is Nr x Nr matrix, V is Nc x Nc matrix and D is non-negative diagonal matrix of Nr x Nt.
Therefore, capacity of N SISO subchannels is sum of individual capacity and results the total MIMO capacity. MIMO capacity varies for different numbers of transmit antennas and receiver antennas. The MATLAB program can calculate the theoretical MIMO capacity of 200 random MIMO channels of different sizes at an SNR of 3 dB. We consider the case a transmitter that does not have the MIMO channel knowledge. Hence, each transmit antenna is allocated the same signal power 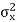 Additionally, the channel noises are assumed to be independent additive white Gaussian with variance
Additionally, the channel noises are assumed to be independent additive white Gaussian with variance 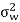 . The entries in the MIMO channel matrix H are randomly generated from Gaussian distribution of zero mean and unit variance. Because the channels are random for M transmit antennas and N receive antennas, the MIMO capacity per y transmission is
. The entries in the MIMO channel matrix H are randomly generated from Gaussian distribution of zero mean and unit variance. Because the channels are random for M transmit antennas and N receive antennas, the MIMO capacity per y transmission is
C = ½ log [IN + 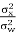 HHT]
HHT]
Because the entries in the MIMO channel Matrix H are randomly generated, its corresponding capacity is also random. From the 200 channels, each N x M MIMO configuration should generate 200 different capacity values. The BER is calculated with respect to single input single output (1 x1) system, single transmitter two receivers (1 x 2), single transmitter and four receivers (1 x 4). The BER analysis and MATLAB simulation expresses that the value of BER is decreasing as the number of receiver antennas are increasing. For the perfect MIMO OFDM system, the BER should be decreased and channel capacity should be increased. The orthogonal nature of the ODDM signal is also simulated. The MIMO OFDM system are the boon for 4G and next generation of the wireless communication systems.
The use of multiple antennas at the transmitter and receiver in wireless systems, popularly known as MIMO (multiple-input multiple-output) technology, has rapidly gained in popularity over the past decade due to its powerful performance-enhancing capabilities. Communication in wireless channels is impaired predominantly by multi-path fading. Multi-path is the arrival of the transmitted signal at an intended receiver through differing angles and/or differing time delays and/or differing frequency (i.e., Doppler) shifts due to the scattering of electromagnetic waves in the environment. Consequently, the received signal power fluctuates in space (due to angle spread) and/or frequency (due to delay spread) and/or time (due to Doppler spread) through the random superposition of the impinging multi-path components. This random fluctuation in signal level, known as fading, can severely affect the quality and reliability of wireless communication. Additionally, the constraints posed by limited power and scarce frequency bandwidth make the task of designing high data rate, high reliability wireless communication systems extremely challenging. MIMO technology constitutes a breakthrough in wireless communication system design. The technology offers a number of benefits that help meet the challenges posed by both the impairments in the wireless channel as well as resource constraints. In addition to the time and frequency dimensions that are exploited in conventional single-antenna (single-input single-output) wireless systems, the leverages of MIMO are realized by exploiting the spatial dimension (provided by the multiple antennas at the transmitter and the receiver).

Figure 2 Average data rate versus SNR for different antenna configurations. The channel bandwidth is 100 kHz.
Benefits of MIMO technology
The benefits of MIMO technology that help achieve such significant performance gains are array gain, spatial diversity gain, spatial multiplexing gain and interference reduction. These gains are described in brief below.
Array gain
Array gain is the increase in receive SNR that results from a coherent combining effect of the wireless signals at a receiver. The coherent combining may be realized through spatial processing at the receive antenna array and/or spatial pre-processing at the transmit antenna array. Array gain improves resistance to noise, thereby improving the coverage and the range of a wireless network.
Spatial diversity gain
As mentioned earlier, the signal level at a receiver in a wireless system fluctuates or fades. Spatial diversity gain mitigates fading and is realized by providing the receiver with multiple (ideally independent) copies of the transmitted signal in space, frequency or time. With an increasing number of independent copies (the number of copies is often referred to as the diversity order), the probability that at least one of the copies is not experiencing a deep fade increases, thereby improving the quality and reliability of reception. A MIMO channel with MT transmit antennas and MR receive antennas potentially offers MTMR independently fading links, and hence a spatial diversity order of MTMR.
Spatial multiplexing gain
MIMO systems offer a linear increase in data rate through spatial multiplexing, i.e., transmitting multiple, independent data streams within the bandwidth of operation. Under suitable channel conditions, such as rich scattering in the environment, the receiver can separate the data streams. Furthermore, each data stream experiences at least the same channel quality that would be experienced by a single-input single-output system, effectively enhancing the capacity by a multiplicative factor equal to the number of streams. In general, the number of data streams that can be reliably supported by a MIMO channel equals the minimum of the number of transmit antennas and the number of receive antennas, i.e., min{MT ,MR}. The spatial multiplexing gain increases the capacity of a wireless network
Interference reduction and avoidance
Interference in wireless networks results from multiple users sharing time and frequency resources. Interference may be mitigated in MIMO systems by exploiting the spatial dimension to increase the separation between users. For instance, in the presence of interference, array gain increases the tolerance to noise as well as the interference power, hence improving the signal-to-noise-plus-interference ratio (SINR). Additionally, the spatial dimension may be leveraged for the purposes of interference avoidance, i.e., directing signal energy towards the intended user and minimizing interference to other users. Interference reduction and avoidance improve the coverage and range of a wireless network. In general, it may not be possible to exploit simultaneously all the benefits described above due to conflicting demands on the spatial degrees of freedom. However, using some combination of the benefits across a wireless network will result in improved capacity, coverage and reliability.
Basic building blocks
Figure shows the basic building blocks that comprise a MIMO communication system. The information bits to be transmitted are encoded (using, for instance, a convolutional encoder) and interleaved. The interleaved codeword is mapped to data symbols (such as quadrature amplitude modulation or QAM symbols) by the symbol mapper. These data symbols are input to a space–time encoder that outputs one or more spatial data streams. The spatial data streams are mapped to the transmit antennas by the space–time precoding block. The signals launched from the transmit antennas propagate through the channel and arrive at the receive antenna array.
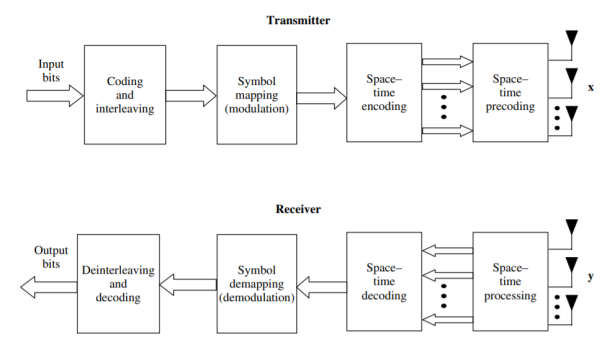
Figure.3 Diagram of a complex equivalent baseband MIMO communication system. x and y stand for the transmitted and received signal vectors respectively.
The receiver collects the signals at the output of each receive antenna element and reverses the transmitter operations in order to decode the data: receive space–time processing, followed by space–time decoding, symbol demapping, deinterleaving and decoding. Each of the building blocks offers the opportunity for significant design challenges and complexity–performance trade-offs. Furthermore, a number of variations can exist in the relative placement of the blocks, the functionality and the interactions between the blocks.
Key takeaway
Communication in wireless channels is impaired predominantly by multi-path fading. Multi-path is the arrival of the transmitted signal at an intended receiver through differing angles and/or differing time delays and/or differing frequency (i.e., Doppler) shifts due to the scattering of electromagnetic waves in the environment. Consequently, the received signal power fluctuates in space (due to angle spread) and/or frequency (due to delay spread) and/or time (due to Doppler spread) through the random superposition of the impinging multi-path components. This random fluctuation in signal level, known as fading, can severely affect the quality and reliability of wireless communication.
MIMO System Model
In the MIMO system which employs multiple antennas in the transmitter and/or receiver, the correlation between transmit and receive antenna is an important aspect of the MIMO channel. It depends on the angle-of-arrival (AoA) of each multi-path component. Consider a SIMO channel with a uniform linear array (ULA) in which M antenna elements are equally spaced apart, with an inter-distance of d as shown in Figure. Let y(t) denote a received signal at the ith antenna element with the channel gain ai , delay ti, and angle of arrival (AoA) fi. As shown in Figure(a), the AoA is defined as the azimuth angle of incoming path with respect to the broadside of the antenna element. Note that the received signal of each path consists of the enormous number of unresolvable signals received around the mean of AoA in each antenna element. A vector of the received signals
Y(t) = [y1(t), y2(t),….yM(t)]T
In the uniform linear array (ULA) of M elements can be expressed as
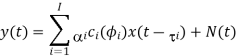
Where I denote the number of paths in each antenna element and c(ɸ) is an array steering vector. The array steering vector is defined as
c(ɸ) = [c1(ɸ), c2(ɸ),….cM(ɸ)]T
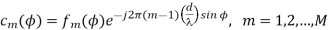
f(ɸ) denotes a complex field pattern of the mth array element and l is the carrier wavelength. The received signal in Equation (3.1) can be expressed in the following integral form:
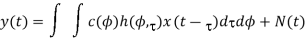
Where h(ɸ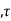 ) represents a channel as a function of ADS (Azimuth-Delay Spread). The
) represents a channel as a function of ADS (Azimuth-Delay Spread). The
Instantaneous power azimuth-delay spectrum (PADS) is given as
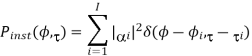
The average PADS is defined as an expected value as
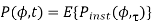
By taking an integral of PADS over delay, PAS (Power Azimuth Spectrum or Power Angular Spectrum) is obtained as
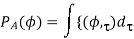
Meanwhile, AS (Azimuth Spread or Angular Spread) is defined by the central moment of PAS, that is

Where f0 is the mean AoA. Similarly, by taking an integral of PADS over AoA, PDS (Power Delay Spectrum) is obtained as
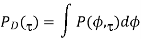
Furthermore, DS (Delay Spread) is defined as the central moment of PDS, that is,

Where t0 is an average delay spread
Once a joint PDF of AoA and delay is given by f ðf; tÞ, the marginal PDF of AoA and delay spread is respectively given as
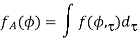
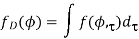
Figure illustrates a MIMO channel model by magnifying a channel environment in Figure. It shows three resolvable paths. Each path hasMr unresolvable paths, each of which arrives centered around the mean AoA. The AoA for these unresolvable paths follow a Gaussian distribution in the microcell or macrocell environment. Furthermore, a power distribution in AoA (i.e., PAS) follows a Laplacian distribution, even though it varies with the cell environment. Note that the natures of AoA and PAS distributions are different from each other. In other words, a distribution of AoA does not take the power of each path into account, while PAS deals with a distribution of the power with respect to AoA. Finally, a distribution of the power for the resolvable paths, that is, PDS or PDP (Power Delay Profile), usually follows an exponential distribution
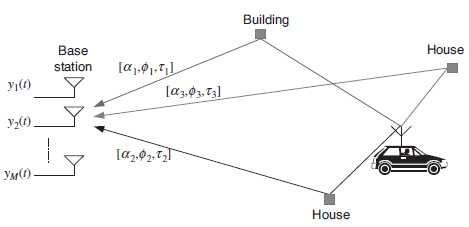
Figure 4 SIMO channel environment
Spatial Correlation
In general, the received signals for each path of the different antenna elements may be spatially correlated, especially depending on the difference in their distances traveled. In this subsection, let us investigate the spatial correlation between the received signals in the different antennas.
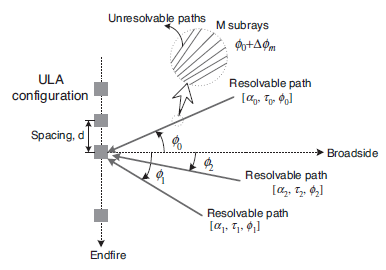
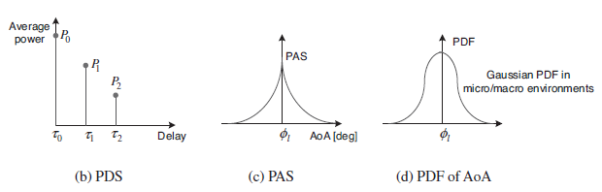
Figure 5 MIMO channel model: an illustration
Consider two omni-directional antennas, a and b, that are spaced apart by d as shown in Figure. For the baseband received signals with the mean AoA of f0, the difference in their distance traveled is given by d sinf0 and the corresponding delay becomes t0 ¼ ðd=cÞ sinf0. Let a and b denote the amplitude and phase of each path, which follow the Rayleigh distribution and uniform distribution over (0,2π)

Figure 6 Signal models for two omni-directional antennas channel, their impulse responses can be respectively represented as
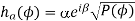
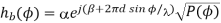
Let us define a spatial correlation function of the received signals with the mean AoA off0 in two antenna elements spaced apart by d as
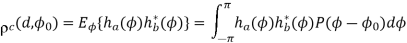
Consider an extreme case that has the mean AoA of ɸ0 =00 and AS of  A=00 that is, P(ɸ-ɸ0)=
A=00 that is, P(ɸ-ɸ0)= , implying that there exists only one sub-ray in a perpendicular direction for each antenna element. In this particular case, AoA does not incur any time difference between ha and hb. Therefore, spatial correlation is always equal to 1, that is,
, implying that there exists only one sub-ray in a perpendicular direction for each antenna element. In this particular case, AoA does not incur any time difference between ha and hb. Therefore, spatial correlation is always equal to 1, that is, 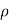 c(d)=E ɸ hah*b. However, in the case that both AoA and AS are not equal to 00, there is a time difference between ha(ɸ) and hb(ɸ) as shown in Equation
c(d)=E ɸ hah*b. However, in the case that both AoA and AS are not equal to 00, there is a time difference between ha(ɸ) and hb(ɸ) as shown in Equation
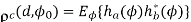
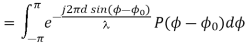
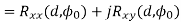
Defining a normalized antenna distance by D=2πd/ , the spatial correlation functions can be written as
, the spatial correlation functions can be written as
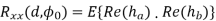
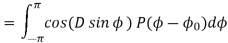
As seen in above equations, spatial correlation between antenna elements depends mainly on the mean AoA and PAS as well as antenna spacing d. In particular, when AS of PAS is small, most sub-rays that compose each path arrive at each antenna from the same angle. It implies that they are correlated with each other since while the magnitudes of two signals become nearly equal, their phases are different by their AoAs.
PAS Model
PAS is an important factor in determining the spatial correlation between antenna elements. It is clear from Equation above section. In fact, a mathematical analysis for spatial correlation requires a distribution of PAS for the real environments. We find that there are various types of PAS models available from the actual measurements of the different channel environments (e.g., indoor or outdoor, macrocell or microcell), including those summarized in Table. A pattern of PAS depends mainly on the distribution of the locally-scattered components. In general, enormous amounts of locally-scattered components are observed by the MS in all different environments. Therefore, its PAS usually follows a uniform distribution. For the BS, however, the different PAS distributions are observed depending on the characteristics of terrain in a cell, which is usually shown to have a small AS. Note that they still show a uniform PAS distribution for the BS in picocells or indoor environments. In the sequel, we will explain in detail the other type of PAS models in Table.
| BS | MS | |
Outdoor |
Macrocell |
|
Uniform |
Microcell | |||
Picocell | Almost Uniform | ||
Indoor | Uniform | ||
I-METRA MIMO Channel Model
A MIMO fading channel can be implemented by using the statistical characteristics, including spatial correlation for PAS. We first discuss the statistical model of the correlated fading channel, which explains a general concept of implementing a MIMO fading channel. Then, we present the I-METRA model which is often adopted for MIMO channel modeling
Statistical Model of Correlated MIMO Fading Channel
Consider a MIMO system with a base station of M antennas and the mobile stations of N antennas as illustrated in Figure. Narrowband MIMO channel H can be statistically expressed with an M X N matrix.
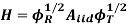
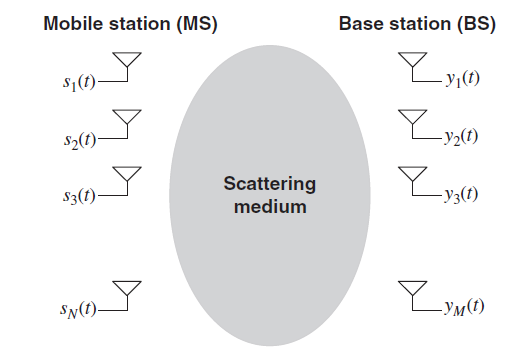
Figure 7 Antenna arrays for MIMO communication.
The transmitter and receiver is sufficiently smaller than a distance between the transmitter and receiver, which is usually true for most of wireless communication environments. The various types of MIMO channels can be generated by adjusting the correlation matrices ΘR and ΘT. As an extreme case, a complete i.i.d. Channel can be generated when ΘR and ΘT are the identity matrices. Furthermore, other extreme types of MIMO channel, including a rank-1 Rician channel and a Rician channel with an arbitrary phase, can also be easily generated with this model.
Now, a broadband MIMO channel can be modeled by a tapped delay line (TDL), which is an extension of the narrowband MIMO channel in Equation
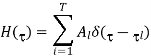
Where Al is the complex channel gain matrix for the lth path with delay 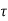 1. Let αlmn be the channel coefficient between the mth BS antenna and the nth MS antenna for the lth path. Assume that αlmn is zero-mean complex Gaussian-distributed, and thus, |αlmn |is Rayleigh-distributed. The complex channel gain matrix Al in Equation is given as
1. Let αlmn be the channel coefficient between the mth BS antenna and the nth MS antenna for the lth path. Assume that αlmn is zero-mean complex Gaussian-distributed, and thus, |αlmn |is Rayleigh-distributed. The complex channel gain matrix Al in Equation is given as
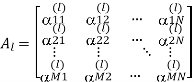
The relation between the MS and BS signals can be expressed as
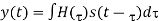
Consider a downlink of MIMO system in Figure. As the antenna spacing at BS is relatively small when Tx and Rx are sufficiently apart, the spatial correlation at MS does not depend on the Tx antenna. In other words, spatial correlation at MS is independent of BS antennas. Then, the correlation coefficient of a channel gain for two different MS antennas, n1 and n2, can be expressed as
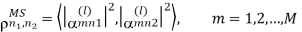

Figure 8 Downlink MIMO System

For the MS in an environment surrounded by local scatters, the spatial correlation becomes negligible when the MS antennas are separated by more than 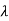 =2. In spite of such a theory, however, the experimental results often show that the channel coefficients with the antennas separated by
=2. In spite of such a theory, however, the experimental results often show that the channel coefficients with the antennas separated by 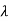 =2 can be highly correlated in some situations, especially in an indoor environment. Let us define a symmetric spatial correlation matrix for the MS as
=2 can be highly correlated in some situations, especially in an indoor environment. Let us define a symmetric spatial correlation matrix for the MS as
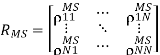
Note that a diagonal component of RMS corresponds to the auto-correlation, which is always given by a correlation coefficient of one. Meanwhile, consider a typical urban environment, where there are no local scatters in the vicinity of the BS antennas, as opposed to MS antennas surrounded by the local scatters. It is attributed to the fact that the BS antennas are usually elevated above the local scatters so as to reduce the path loss. In this case, the PAS at the BS is subject to a relatively narrow beamwidth. Consider an uplink MIMO system in Figure. As long as Tx and Rx are sufficiently apart, all MS antennas that are closely co-located tend to have the same radiation pattern, illuminating the same surrounding scatters. Then, it also makes the spatial correlation of BS antennas independent of MS antennas and thus, the
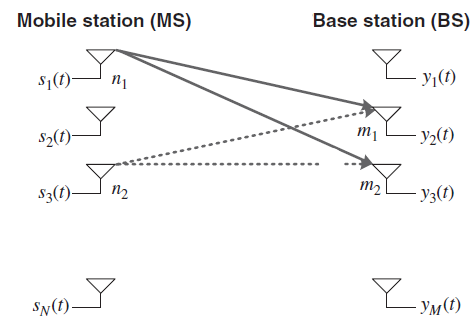
Fig 9 Uplink MIMO System
Correlation coefficient of a channel gain for two different BS antennas, m1 and m2, can be
Expressed as
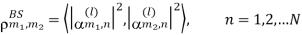
Let us define the spatial correlation matrix for the BS as

In order to generate the channel gain matrix Al in Equation above, information on the channel correlation between the Tx and Rx antennas is required. In fact, the spatial correlation matrices at BS and MS, RBS and RMS, do not provide sufficient information to generate Al . In fact, as illustrated in Figure below, the correlation of coefficients between the pairs of Tx and Rx, αm1n1 and αm2n2, is additionally required, i.e.,
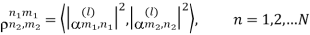
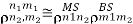
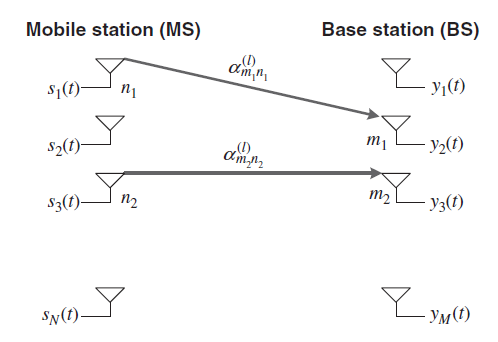
Figure 10 Correlation between Tx and Rx antennas
I-METRA (Intelligent Multi-element Transmit and Receive Antennas) MIMO channel model has been proposed by a consortium of the industries and universities, including Nokia. It is based on a stochastic MIMO channel model, which generates a correlated MIMO fading channel using the spatial correlation derived for ULA (Uniform Linear Array) subject to a single or multiple clusters with the Uniform Truncated Gaussian, or Truncated Laplacian PAS.
In the current discussion, the Truncated Gaussian and Truncated Laplacian PAS models are simply referred to as Gaussian and Laplacian PAS, respectively. The overall procedure for the I-METRA MIMO channel modeling consists of two main steps as shown in Figure. In the first step, the BS and MS spatial correlation matrices (RBS and RMS) and normalization factor are determined for the specified channel configuration, including the number of BS and MS antennas, antenna spacing, the number of clusters, PAS, AS, and AoA.
The spatial correlation matrix R for uplink or downlink is determined. In the second step, a symmetric mapping matrix Cis found by Equation above and then, the correlated fading MIMO channel is generated by multiplying it by the power per path and the uncorrelated fading signal. Once the correlated MIMO channel coefficients are generated for each path by following the procedure in Figure, the overall MIMO channel is simulated by using a tapped delay line.
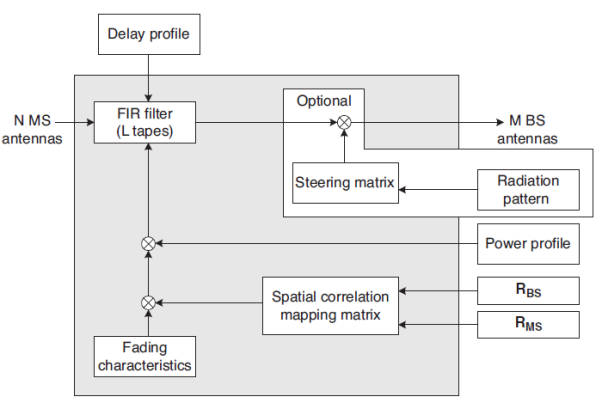
Figure 11 Functional block diagram for I-METRA MIMO channel model
Figure above shows a functional block diagram that implements the overall MIMO channel characteristics, taking the delay and power profiles into account. Here, an uncorrelated fading channel is generated with the pre-stored Doppler spectrum. It is multiplied by a spatial correlation mapping matrix to generate a correlated fading channel. The given PDP characteristics are implemented by passing the correlated fading signal through a FIR filter that is designed to satisfy the given average power and delay specification for each path. Furthermore, antenna radio pattern can be adjusted by generating a steering matrix. Some of these attributes are detailed in the sequel.
Rician Fading for a MIMO Channel
In contrast with Rician fading in the SISO channel, a phase change in each LOS path between the different antennas must be taken into account for modeling a Rician fading process in the MIMO channel. As shown in Figure below, the Rician fading process can be modeled by the sum of two matrices, each of which are weighed by the power ratio between the LOS signal and the scattered signal, respectively. A matrix for the Rician fading channel of the first path, H1, can be represented as
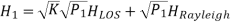
Where P1 denotes the average power of the first path and K is a power ratio of the LOS to Rayleigh components. Furthermore, HLOS represents the LOS component, which is defined as
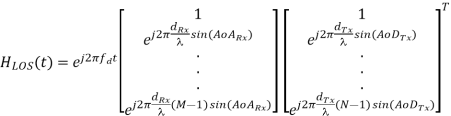
Where α is an angle between the Direction-of-Movement (DoM) and LOS component. Meanwhile, drx and dtx denote the antenna spacing in the receiver and transmitter, respectively. Furthermore, AoArx and AoDtx represent the Angle-of-Arrival at the receiver and the Angle-of-Departure at the transmitter, respectively.
Figure 12 Signal model for a Rician fading MIMO channel.
3GPP MIMO Channel Model
Table below presents the channel parameters for the I-METRA MIMO channel that had been proposed in 3GPP. UE (User Equipment) and Node B in this table refers to the MS (mobile station) and BS (base station), respectively. Case A corresponds to the frequency-nonselective Rayleigh fading environment without any correlation among all antenna elements, which can be used as a simple reference model. Case B and Case C deal with the typical urban macrocell environment with the different delay spread, in which each delay component is coming from the same AoA. Case D models the microcell and bad urban environments with each delay component from the different AoA. We assume that all channel taps (paths) are subject to Rayleigh fading. In order to model the LOS situation, however, the first tap of the channel models for Case B and Case C may be subject to Rician fading. Meanwhile, the different PDPs of ITU mobility model are employed for the different cases.
For 4X4 MIMO channel model with antenna spacing of 0.5 in Table, the complex spatial correlation matrices in the BS and MS are found. For the different cases in Table where BS and MS have the different spatial characteristics in terms of PAS and AoA, the specific spatial correlation matrices are given as follows:
in Table, the complex spatial correlation matrices in the BS and MS are found. For the different cases in Table where BS and MS have the different spatial characteristics in terms of PAS and AoA, the specific spatial correlation matrices are given as follows:
Case B: BS with Laplacian PAS for AS =50 and AoA =200, MS with Uniform PAS for AoA =22.50

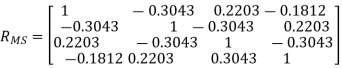
Case C: BS with Laplacian PAS for AS = 100 and AoA = 200, MS with Laplacian PAS for AS=350 and AoA = 67.50
|
| Case A Rayleigh uncorrelated | Case B Macrocell | Case C macrocell | Case D microcell/bad-urban |
| Number of paths | 1 | 4 | 6 | 6 |
| PDP | N/A | ITU Pedestrian A | ITU Vehicular A | ITU Pedestrian B |
| Doppler spectrum | Classical | Classical | Laplacian | Laplacian |
| Speed(km/h) | 3/40/120 | 3/40/120 | 3/40/120 | 3/40/120 |
UE (MS) | Topology | N/A | 0.5 spacing | 0.5 spacing | 0.5 spacing |
PAS | N/A | Path#1, Rician K=6dB 9uniform over 360°) | Laplacian AS=35° (uniform over 360°) | Laplacian AS=35° (uniform over 360°) | |
DoM(deg) | N?A | 0 | 22.5 | -22.5 | |
AoA(deg) | N/A | 22.5(all paths) | 67.5(all paths) | 22.5 (odd paths) -67.5 even paths) | |
Node B (BS) | Topology | N/A | ULA: (1) 0.5 spacing (2) 4.0 spacing | ULA: (1) 0.5 spacing (2) 4.0 spacing | ULA: (1) 0.5 spacing (2) 4.0 spacing |
PAS | N/A | Laplacian AS=5° | Laplacian AS=10° | Laplacian AS=15° | |
AoA(deg) | N/A | 20,50° | 20,50° | 2,-20,10,-8,-3,3  |


Case D: BS with Laplacian PAS for AS = 150 and AoA =200, MS with Laplacian PAS for AS = 350 and AoA = 22.50/-67.50 (even path/odd path)


Spatial Correlation of Ray-Based Channel Model
In general, the channel coefficients of two antenna elements can be correlated both in the temporal and spatial domains. Spatial correlation is the cross-correlation of the signals that originate from the same source and are received at two spatially separated antenna elements. Consider a spatial channel model for the uniform linear array antenna in which all antenna elements are equally spaced apart with a distance of d, as illustrated in Figure below. Here, spatial correlation between two adjacent antenna elements for the nth path is given by
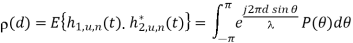
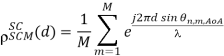

Figure 13 Signal model for uniform linear array (ULA) antenna.
MIMO-OFDM
With the ever-increasing number of wireless subscribers and their seemingly “greedy” demands for high-data-rate services, radio spectrum becomes an extremely rare and invaluable resource for all the countries in the world. Efficient use of radio spectrum requires that modulated carriers be placed as close as possible without causing any ICI and be capable of carrying as many bits as possible. Optimally, the bandwidth of each carrier would be adjacent to its neighbors, so there would be no wasted bands. In practice, a guard band must be placed between neighboring carriers to provide a guard space where a shaping filter can attenuate a neighboring carrier’s signal.
These guard bands are waste of spectrum. In order to transmit high-rate data, short symbol periods must be used. The symbol period Tsym is the inverse of the baseband data rate R (R = 1/Tsym), so as R increases, Tsym must decrease. In a multipath environment, however, a shorter symbol period leads to an increased degree of ISI, and thus performance loss. OFDM addresses both of the two problems with its unique modulation and multiplexing technique. OFDM divides the high-rate stream into parallel lower rate data and hence prolongs the symbol duration, thus helping to eliminate ISI. It also allows the bandwidth of subcarriers to overlap without ICI as long as the modulated carriers are orthogonal. OFDM therefore is considered as a good candidate modulation technique for broadband access in a very dispersive environment.
However, relying solely on OFDM technology to improve the spectral efficiency gives us only a partial solution. At the end of 1990s, seminal work by Foshini and Gans and, independently, by Teltar showed that there is another alternative to accomplish high-data-rate over wireless channels: the use of multiple antennas at the both ends of the wireless link, often referred to as MA (multiple antenna) or MIMO in the literature. The MIMO technique does not require any bandwidth expansions or any extra transmission power. Therefore, it provides a promising means to increase the spectral efficiency of a system. In his paper about the capacity of multi-antenna Gaussian channels, Telatar showed that given a wireless system employing Nt TX (transmit) antennas and Nr RX (receive) antennas, the maximum data rate at which error-free transmission over a fading channel is theoretically possible is proportional to the minimum of Nt and Nr (provided that the Nt Nr transmission paths between the TX and RX antennas are statistically independent). Hence huge throughput gains may be achieved by adopting Nt × Nr MIMO systems compared to conventional 1 × 1 systems that use single antenna at both ends of the link with the same requirement of power and bandwidth. With multiple antennas, a new domain,namely, the spatial domain is explored, as opposed to the existing systems in which the time and frequency domain are utilized.
The combination of MIMO systems with OFDM technology provides a promising candidate for next generation fixed and mobile wireless systems. In practice for coherent detection, however, accurate channel state information in terms of channel impulse response (CIR) or channel frequency response (CFR) is critical to guarantee the diversity gains and the projected increase in data rate. The channel state information can be obtained through two types of methods. One is called blind channel estimation, which explores the statistical information of the channel and certain properties of the transmitted signals.
The other is called training-based channel estimation, which is based on the training data sent at the transmitter and known a priori at the receiver. Though the former has its advantage in that it has no overhead loss, it is only applicable to slowly time-varying channels due to its need for a long data record. Our work in this thesis focuses on the training-based channel estimation method, since we aim at mobile wireless applications where the channels are fast time-varying. The conventional training-based method is used to estimate the channel by sending first a sequence of OFDM symbols, so-called preamble which is composed of known training symbols.
Then the channel state information is estimated based on the received signals corresponding to the known training OFDM symbols prior to any data transmission in a packet. The channel is hence assumed to be constant before the next sequence of training OFDM symbols. A drastic performance degradation then arises if applied to fast time-varying channels. In optimal pilot-tone selection and placement were presented to aid channel estimation of single-input/single-output (SISO) systems. To use a set of pilot-tones within each OFDM block, not a sequence of training blocks ahead of a data packet to estimate the time-varying channel is the idea behind our work. However direct generalization of the channel estimation algorithm in to MIMO-OFDM systems involves the inversion of a high-dimension matrix due to the increased number of transmit and receive antennas, and thus entails high complexity and makes it infeasible for wireless communications over highly mobile channels. This becomes a bottleneck for applications to broadband wireless communications.
The block diagram of a MIMO-OFDM system is shown in Figure. Basically, the MIMO-OFDM transmitter has Nt parallel transmission paths which are very similar to the single antenna OFDM system, each branch performing serial-to-parallel conversion, pilot insertion, N-point IFFT and cyclic extension before the final TX signals are up-converted to RF and transmitted. It is worth noting that the channel encoder and the digital modulation, in some spatial multiplexing systems, can also be done per branch, not necessarily implemented jointly over all the Nt branches. The receiver first must estimate and correct the possible symbol timing error and frequency offsets, e.g., by using some training symbols in the preamble as standardized. Subsequently, the CP is removed and N-point FFT is performed per receiver branch.
In this thesis, the channel estimation algorithm we proposed is based on single carrier processing that implies MIMO detection has to be done per OFDM subcarrier. Therefore, the received signals of subcarrier k are routed to the kth MIMO detector to recover all the Nt data signals transmitted on that subcarrier. Next, the transmitted symbol per TX antenna is combined and outputted for the subsequent operations like digital demodulation and decoding. Finally, all the input binary data are recovered with certain BER.
As a MIMO signalling technique, Nt different signals are transmitted simultaneously over Nt × Nr transmission paths and each of those Nr received signals is a combination of all the Nt transmitted signals and the distorting noise. It brings in the diversity gain for enhanced system capacity as we desire. Meanwhile compared to the SISO system, it complicates the system design regarding to channel estimation and symbol detection due to the hugely increased number of channel coefficients.
Signal Model
To find the signal model of MIMO-OFDM system, we can follow the same approach as utilized in the SISO case. Because of the increased number of antennas, the signal dimension is changed. For instance, the transmitted signal on the k-th subcarrier in a MIMO system is an Nt × 1 vector, instead of a scalar in the SISO case. For brevity of presentation, the same notations are used for both the SISO and MIMO cases. But they are explicitly defined in each case. There are Nt transmit antennas and hence on each of the N subcarriers, Nt modulated signals are transmitted simultaneously. Denote  (m) and
(m) and  (mN + k) as the m-th modulated OFDM symbol in frequency domain and the k-th modulated subcarrier respectively as
(mN + k) as the m-th modulated OFDM symbol in frequency domain and the k-th modulated subcarrier respectively as
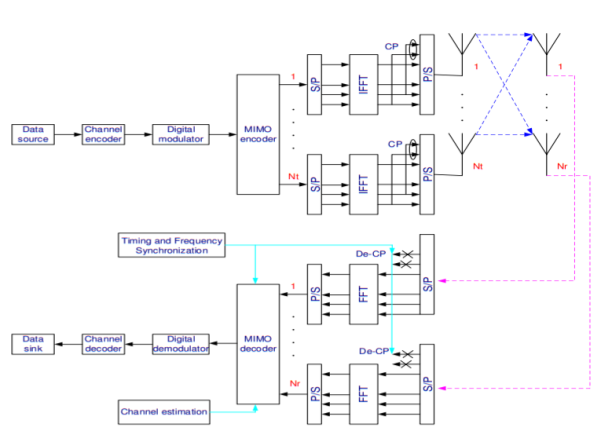
Fig 14 MIMO-OFDM System model

Where Sj (mN + k) represents the k-th modulated subcarrier for the m-th OFDM symbol transmitted by the j-th antenna. And it is normalized by a normalization factor KMOD so that there is a unit normalized average power for all the mappings. Taking IFFT of 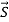 (m) as a baseband modulation, the resulting time-domain samples can be expressed as
(m) as a baseband modulation, the resulting time-domain samples can be expressed as
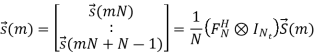

Here IFFT is a block-wise operation since each modulated subcarrier is a column vector and the generalized NNt-point IFFT matrix is a Kronecker product of FN and INt. This is just a mathematical expression. In the real OFDM systems, however, the generalized IFFT operation is still performed by Nt parallel N-point IFFT. To
Eliminate the ISI and the ICI, a length-Ng (Ng ≥ L) CP is prepended to the time domain samples per branch. The resulting OFDM symbol 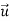 (m) is denoted as
(m) is denoted as

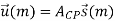
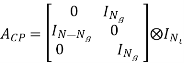
The time-domain samples denoted by ~u(m) may be directly converted to RF for transmission or be up-converted to IF first and then transmitted over the wireless MIMO channel. For the MIMO channel, we assume in this thesis that the MIMOOFDM system is operating in a frequency-selective Rayleigh fading environment and that the communication channel remains constant during a frame transmission, i.e., quasi-static fading. Suppose that the channel impulse response can be recorded with L time instances, i.e., time samples, then the multipath fading channel between the j-th TX and i-th RX antenna can be modeled by a discrete-time complex baseband equivalent (L − 1)-th order FIR filter with filter coefficients hij (l, m), with l ⊆ {0, . . . , L − 1} and integer m > 0. As assumed in SISO case, these CIR coefficients {hij (0, m), . . . , hij (L − 1, m)} are independent complex zero-mean Gaussian RV’s with variance 1 2Pl per dimension. The total power of the channel power delay profile {P0, . . . ,PL−1} is normalized to be σ 2c = 1. Let hm be the CIR matrix and denote hl,m as the l-th matrix-valued CIR coefficient.

In addition, we assume that those NtNr geographically co-located multipath channels are independent in an environment full of scattering. In information-theoretic point of view, it guarantees the capacity gain of MIMO systems. For the practical MIMO-OFDM systems, it enforces a lower limit on the shortest distance between multiple antennas at a portable receiver unit. If the correlation between those channels exists, the diversity gain from MIMO system will be reduced and hence system performance is degraded. At the receive side, an Nr-dimensional complex baseband equivalent receive signal can be obtained by a matrix-based discrete-time convolution as
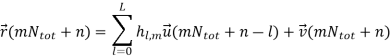
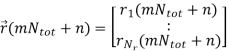

The expected signal-to-noise ratio (SNR) per receive antenna is Nt σ2v. In order to have a fair comparison with SISO systems, the power per TX antenna should be scaled down by a factor of Nt . By stacking the received samples at discrete time instances, 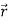 (m) can be described by
(m) can be described by
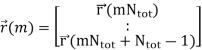
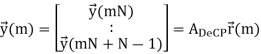
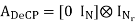
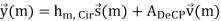
Where hm,Cir is an NNr × NNt block circulant matrix. In general, an NNr × NNt block circulant matrix is fully defined by its first NNr × Nt block matrices. In our case, hm,Cir is determined by
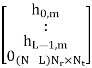
Finally taking FFT on the  (m) at the receiver, we obtain the frequency domain MIMO-OFDM baseband signal model
(m) at the receiver, we obtain the frequency domain MIMO-OFDM baseband signal model

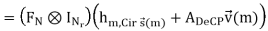
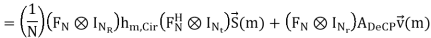
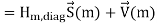
In the above expression, V~ (m) represents the frequency domain noise, which is i.i.d. (independent and identically distributed) zero-mean and complex Gaussian random variable with variance 1/2 σ 2v per dimension, and Hm,diag is a block diagonal matrix which is given by
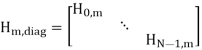
The k-th block diagonal element is the frequency response of the MIMO channel at the k-th subcarrier and can be shown to be
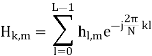
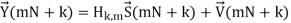
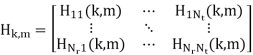
This leads to a flat-fading signal model per subcarrier and it is similar to the SISO signal model, except that Hk,m is an Nr × Nt matrix.
Key takeaway
The combination of MIMO systems with OFDM technology provides a promising candidate for next generation fixed and mobile wireless systems. In practice for coherent detection, however, accurate channel state information in terms of channel impulse response (CIR) or channel frequency response (CFR) is critical to guarantee the diversity gains and the projected increase in data rate.
References:
1. Cristopher Cox, “An Introduction to LTE: LTE, LTE-Advanced, SAE, VoLTE and 4G Mobile Communications”, Wiley, 2nd Edition.
2. E. Dahlman, J. Skold, and S. Parkvall, “4G, LTE-Advanced Pro and The Road to 5G”, Academic Press, 3rd Edition.
3. B. P. Lathi, “Modern Digital and Analog Communications Systems”. Oxford university press, 2015, 4th Edition.
4. Obaidat, P. Nicopolitids, “Modeling and simulation of computer networks and systems: Methodologies and applications” Elsevier, st Edition.