Unit - 3
Digital Modulation-II
QAM (also known as QASK) is a combination of ASK and PSK. Here, both the amplitude and the phase are varied to transmit more bits per symbol.
The QAM modulator essentially follows the idea that can be seen from the basic QAM theory where there are two carrier signals with a phase shift of 90° between them. These are then amplitude modulated with the two data streams known as the I or In-phase and the Q or quadrature data streams. These are generated in the baseband processing area.
Basic QAM I-Q modulator circuit
The two resultant signals are summed and then processed as required in the RF signal chain, typically converting them in frequency to the required final frequency and amplifying them as required.
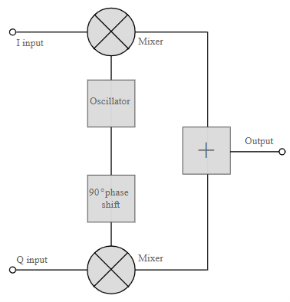
Fig.1: Basic QAM
It is worth noting that as the amplitude of the signal varies any RF amplifiers must be linear to preserve the integrity of the signal. Any non-linearities will alter the relative levels of the signals and alter the phase difference, thereby distorting he signal and introducing the possibility of data errors.
Basic QAM I-Q demodulator circuit
The basic modulator assumes that the two quadrature signals remain exactly in quadrature.
A further requirement is to derive a local oscillator signal for the demodulation that is exactly on the required frequency for the signal. Any frequency offset will be a change in the phase of the local oscillator signal with respect to the two double sideband suppressed carrier constituents of the overall signal.
Systems include circuitry for carrier recovery that often utilises a phase locked loop - some even have an inner and outer loop. Recovering the phase of the carrier is important otherwise the bit error rate for the data will be compromised.
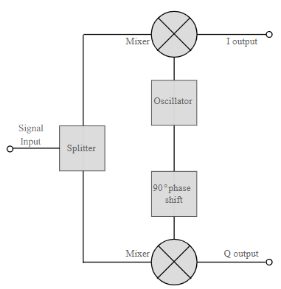
Fig.2: Basic QAM demodulator
The circuits shown above show the generic IQ QAM modulator and demodulator circuits that are used in a vast number of different areas. Not only are these circuits made from discrete components, but more commonly they are used within integrated circuits that are able to provide a large number of functions.
Error Probability
BER for QAM constellation
The SER for a rectangular M-QAM (16-QAM, 64-QAM, 256-QAM etc) with size L = M2 can be calculated by considering two M-PAM on in-phase and quadrature components. The error probability of QAM symbol is obtained by the error probability of each branch (M-PAM) and is given by
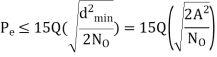
Signal Space Representation
For the case when M = 2k, k even, the resulting signal space diagram has a “square constellation.” In this case the QAM signal can be thought of as 2 PAM signals in quadrature. For M = 2k, k odd, the constellation takes on a “cross” form. For example, 16-QAM constellation is
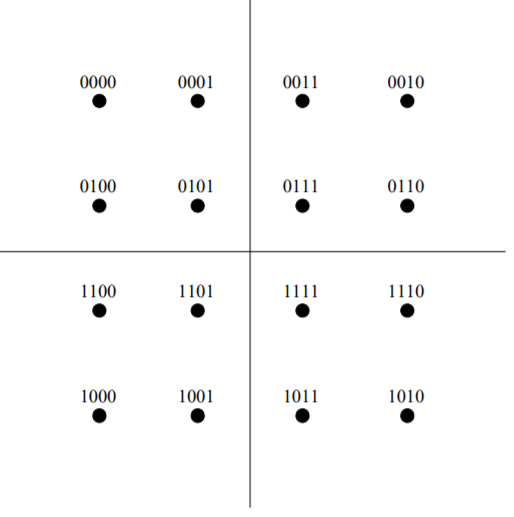
Fig 3:16-QAM constellation
Key takeaway
QAM (also known as QASK) is a combination of ASK and PSK. Here, both the amplitude and the phase are varied to transmit more bits per symbol.
Consider next the M-ary version of FSK, for which the transmitted signals are defined by
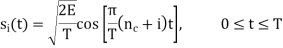
Where i = 1, 2, , M, and the carrier frequency fc = nc/(2T) for some fixed integer nc. The transmitted symbols are of equal duration T and have equal energy E. Since the individual signal frequencies are separated by 1/(2T) Hz, the M-ary FSK signals constitute an orthogonal set; that is,
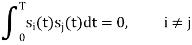
Hence, we may use the transmitted signals si (t) themselves, except for energy normalization, as a complete orthonormal set of basis functions, as shown by
 for
for 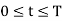 and
and 
Accordingly, the M-ary FSK is described by an M-dimensional signal-space diagram. For the coherent detection of M-ary FSK signals, the optimum receiver consists of a bank of M correlators or matched filters, with i (t) providing the basis functions. At the sampling times t = kT, the receiver makes decisions based on the largest matched filter output in accordance with the maximum likelihood decoding rule. An exact formula for the probability of symbol error is, however, difficult to derive for a coherent M-ary FSK system. Nevertheless, we may use the union bound to place an upper bound on the average probability of symbol error for M-ary FSK. Specifically, since the minimum distance dmin in M-ary FSK is √2E, we have
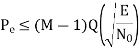
For fixed M, this bound becomes increasingly tight as the ratio EN0 is increased. Indeed, it becomes a good approximation to Pe for values of Pe 10–3.
Power Spectra of M-ary FSK Signals
The spectral analysis of M-ary FSK signals is much more complicated than that of M-ary PSK signals. A case of particular interest occurs when the frequencies assigned to the multilevel make the frequency spacing uniform and the frequency deviation h = 12. That is, the M signal frequencies are separated by 1/2T, where T is the symbol duration. For h = 12, the baseband power spectral density of M-ary FSK signals is plotted in Figure below for M = 2, 4, 8.
Bandwidth Efficiency of M-ary FSK Signals
When the orthogonal signals of an M-ary FSK signal are detected coherently, the adjacent signals need only be separated from each other by a frequency difference 12T so as to maintain orthogonality. Hence, we may define the channel bandwidth required to transmit M-ary FSK signals as
B=M/2T
For multilevels with frequency assignments that make the frequency spacing uniform and equal to 1/2T, the bandwidth B contains a large fraction of the signal power.
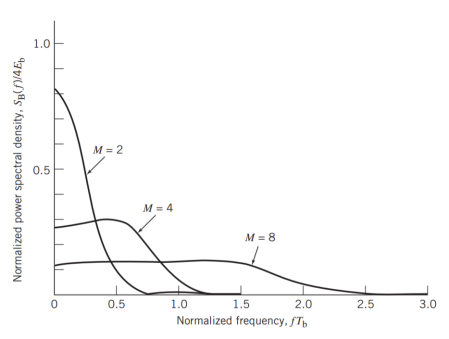
Fig 4: Power spectra of M-ary PSK signals for M = 2, 4, 8.[5]
Hence, using Rb=1/Tb, we may redefine the channel bandwidth B for M-ary FSK signals as

The bandwidth efficiency of M-ary signals is therefore
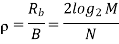
Key takeaway
When the orthogonal signals of an M-ary FSK signal are detected coherently, the adjacent signals need only be separated from each other by a frequency difference 12T so as to maintain orthogonality. Hence, we may define the channel bandwidth required to transmit M-ary FSK signals as
B=M/2T
In the coherent detection of binary FSK signal, the phase information contained in the received signal is not fully exploited, other than to provide for synchronization of the receiver to the transmitter. We now show that by proper use of the continuous-phase property when performing detection, it is possible to improve the noise performance of the receiver significantly. Here again, this improvement is achieved at the expense of increased system complexity. Consider a continuous-phase frequency-shift keying (CPFSK) signal, which is defined for the signaling interval 0 t Tb as follows:

Where Eb is the transmitted signal energy per bit and Tb is the bit duration.
Another useful way of representing the CPFSK signal s(t) is to express it as a conventional angle-modulated signal:
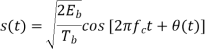
Where (t) is the phase of s(t) at time t. When the phase (t) is a continuous function of time, we find that the modulated signal s(t) is itself also continuous at all times, including the inter-bit switching times. The phase (t) of a CPFSK signal increases or decreases linearly with time during each bit duration of Tb seconds, as shown by
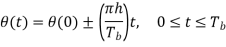
Here the plus sign corresponds to sending symbol 1 and the minus sign corresponds to sending symbol 0; the dimensionless parameter h is to be defined. We deduce the following pair of relations:
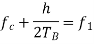
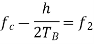
Solving this pair of equations for fc and h, we get

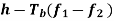
Signal-Space Diagram of MSK
Using a well-known trigonometric identity of conventional angle modulated signal, we may expand the CPFSK signal s(t) in terms of its in-phase and quadrature components as
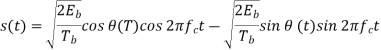
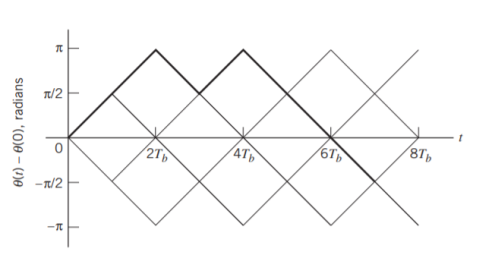
Fig 5: Boldfaced path represents the sequence 1101000.
Consider, first, the in-phase component √2Eb/Tbcos(t)
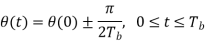
Where the plus sign corresponds to symbol 1 and the minus sign corresponds to symbol 0. A similar result holds for (t) in the interval –Tb t 0, except that the algebraic sign is not necessarily the same in both intervals. Since the phase (0) is 0 or depending on the past history of the modulation process, we find that in the interval –Tb t Tb, the polarity of cos(t) depends only on (0), regardless of the sequence of 1s and 0s transmitted before or after t = 0. Thus, for this time interval, the in-phase component consists of the half-cycle cosine pulse:

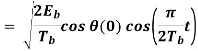
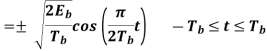
Where the plus sign corresponds to (0) = 0 and the minus sign corresponds to (0) = . In a similar way, we may show that, in the interval 0 t 2Tb, the quadrature component of s(t) consists of the half-cycle sine pulse:
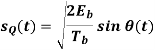
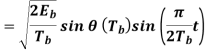
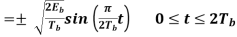
Where the plus sign corresponds to (Tb) = 2 and the minus sign corresponds to (Tb)=–2. From the discussion just presented, we see that the in-phase and quadrature components of the MSK signal differ from each other in two important respects:
- They are in phase quadrature with respect to each other and
- The polarity of the in-phase component sI(t) depends on (0), whereas the polarity of the quadrature component sQ(t) depends on (Tb).
Moreover, since the phase states (0) and (Tb) can each assume only one of two possible values, any one of the following four possibilities can arise:
1. (0) = 0 and (Tb) = /2, which occur when sending symbol 1.
2. (0) = and (Tb) = /2, which occur when sending symbol 0.
3. (0) = and (Tb) = –/2 (or, equivalently, 3/2 modulo 2), which occur when sending symbol 1.
4. (0) = 0 and (Tb) = –/2, which occur when sending symbol 0.
This fourfold scenario, in turn, means that the MSK signal itself can assume one of four possible forms, depending on the values of the phase-state pair: (0) and (Tb).
Signal-Space Diagram
We see that there are two orthonormal basis functions 1(t) and 2(t) characterizing the generation of MSK; they are defined by the following pair of sinusoidally modulated quadrature carriers:
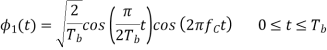
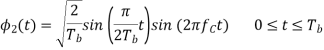

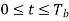
Where the coefficients s1 and s2 are related to the phase states (0) and (Tb), respectively. To evaluate s1, we integrate the product s(t)1(t) with respect to time t between the limits –Tb and Tb, obtaining
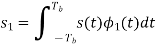
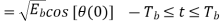
Similarly, to evaluate s2 we integrate the product s(t)2(t) with respect to time t between the limits 0 and 2Tb, obtaining

From above two equations we conclude that
1. Both integrals are evaluated for a time interval equal to twice the bit duration.
2. The lower and upper limits of the integral used to evaluate s1 are shifted by the bit duration Tb with respect to those used to evaluate s2.
3. The time interval 0 t Tb, for which the phase states (0) and (Tb) are defined, is common to both integrals.
It follows, therefore, that the signal constellation for an MSK signal is two-dimensional (i.e., N = 2), with four possible message points (i.e., M = 4), as illustrated in the signal space diagram of Figure below.
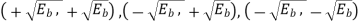 and
and 
The possible values of (0) and (Tb), corresponding to these four message points, are also included in Figure below. The signal-space diagram of MSK is thus similar to that of QPSK in that both of them have four message points in a two-dimensional space. However, they differ in a subtle way that should be carefully noted:
- QPSK, moving from one message point to an adjacent one, is produced by sending a two-bit symbol (i.e., dibit).
- MSK, on the other hand, moving from one message point to an adjacent one, is produced by sending a binary symbol, 0 or 1. However, each symbol shows up in two opposite quadrants, depending on the value of the phase-pair: (0) and (Tb).
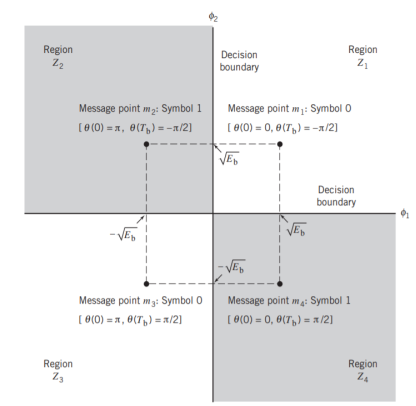
Fig 6: Signal-space diagram for MSK system
Generation and Coherent Detection of MSK Signals
With h = 1/2, we may use the block diagram of Figure(a) below to generate the MSK signal. The advantage of this method of generating MSK signals is that the signal coherence and deviation ratio are largely unaffected by variations in the input data rate. Two input sinusoidal waves, one of frequency fc = nc4Tb for some fixed integer nc and the other of frequency 14Tb, are first applied to a product modulator. This modulator produces two phase-coherent sinusoidal waves at frequencies f1 and f2, which are related to the carrier frequency fc and the bit rate 1/Tb in accordance with above equations for deviation ratio h = 12. These two sinusoidal waves are separated from each other by two narrowband filters, one centered at f1 and the other at f2. The resulting filter outputs are next linearly combined to produce the pair of quadrature carriers or orthonormal basis functions 1(t) and 2(t). Finally, 1(t) and 2(t) is multiplied with two binary waves a1(t) and a2(t), both of which have a bit rate equal to 1/(2Tb)
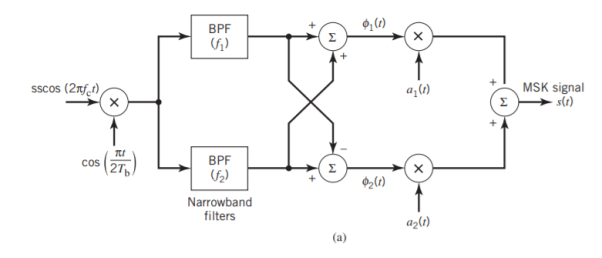
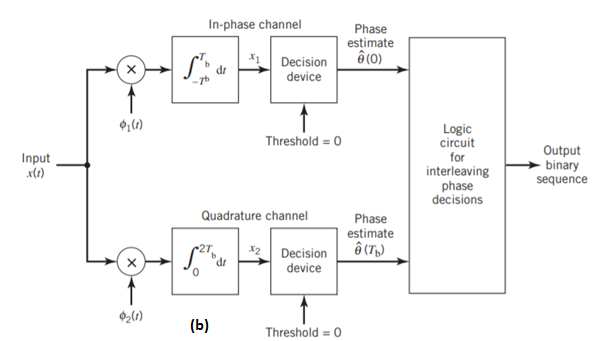
Fig 7: Block diagrams for (a) MSK transmitter and (b) coherent MSK receiver
Figure (b) above shows the block diagram of the coherent MSK receiver. The received signal x(t) is correlated with 1(t) and 2(t). In both cases, the integration interval is 2Tb seconds, and the integration in the quadrature channel is delayed by Tb seconds with respect to that in the in-phase channel. The resulting in-phase and quadrature channel correlator outputs, x1 and x2, are each compared with a threshold of zero
Error Probability of MSK
In the case of an AWGN channel, the received signal is given by
x(t) = s(t) + w(t)
Where s(t) is the transmitted MSK signal and w(t) is the sample function of a white Gaussian noise process of zero mean and power spectral density N0/2. To decide whether symbol 1 or symbol 0 was sent in the interval 0 t Tb, say, we have to establish a procedure for the use of x(t) to detect the phase states (0) and (Tb). For the optimum detection of (0), we project the received signal x(t) onto the reference signal over the interval –Tb t Tb, obtaining
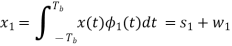
w1 is the sample value of a Gaussian random variable of zero mean and variance N0/2. From the signal-space diagram, we see that if x1 > 0, the receiver chooses the estimate. On the other hand, if x1 0, it chooses the estimate. Similarly, for the optimum detection of (Tb), we project the received signal x(t) onto the second reference signal 2(t) over the interval 0 t 2Tb, obtaining
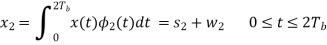
w2 is the sample value of another independent Gaussian random variable of zero mean and variance N02. Referring again to the signal space diagram, we see that if x2 0, the receiver chooses the estimate Tb = – 2. If, however, x2 0, the receiver chooses the estimate ˆ Tb = 2
It follows, therefore, that the BER for the coherent detection of MSK signals is given by
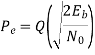
Key takeaway
- In M-ary PSK using coherent detection, increasing M improves the bandwidth efficiency, but the Eb/N0 required for the idealized condition of “error-free” transmission moves away from the Shannon limit as M is increased.
- In M-ary FSK, as the number of frequency-shift levels M is increased—which is equivalent to increased channel-bandwidth requirement—the operating point moves closer to the Shannon limit.
Pulse shaping is the process of changing the waveform of transmitted pulses. Its purpose is to make the transmitted signal better suited to its purpose or the communication channel, typically by limiting the effective bandwidth of the transmission.
In communications systems, two important requirements of a wireless communications channel demand the use of a pulse shaping filter. These requirements are:
1) Generating bandlimited channels, and
2) r\Reducing inter symbol interference (ISI) from multi-path signal reflections. Both requirements can be accomplished by a pulse shaping filter which is applied to each symbol.
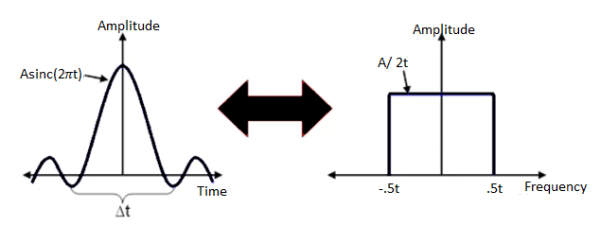
Fig 8: Time v/s Frequency Domain of Sinc Pulse
In fact, the sinc pulse, shown below, meets both of these requirements because it efficiently utilizes the frequency domain to utilize a smaller portion of the frequency domain, and because of the windowing affect that it has on each symbol period of a modulated signal. A sinc pulse is shown below along with an FFT spectrum of the given signal.
Inter-symbol Interference
This is a form of distortion of a signal, in which one or more symbols interfere with subsequent signals, causing noise or delivering a poor output.
Causes of ISI
The main causes of ISI are −
- Multi-path Propagation
- Non-linear frequency in channels
The ISI is unwanted and should be completely eliminated to get a clean output. The causes of ISI should also be resolved in order to lessen its effect.
To view ISI in a mathematical form present in the receiver output, we can consider the receiver output.
The receiving filter output y(t)y(t) is sampled at time ti=iTb (with i taking on integer values), yielding –
y(ti)= μ∑akp(iTb−kTb)
= μai+μ∑akp(iTb−kTb)
In the above equation, the first term μai is produced by the ith transmitted bit.
The second term represents the residual effect of all other transmitted bits on the decoding of the ith bit. This residual effect is called as Inter Symbol Interference.
In the absence of ISI, the output will be −
y(ti)=μai
This equation shows that the ith bit transmitted is correctly reproduced. However, the presence of ISI introduces bit errors and distortions in the output.
While designing the transmitter or a receiver, it is important that you minimize the effects of ISI, so as to receive the output with the least possible error rate.
Key takeaway
The main causes of ISI are −
- Multi-path Propagation
- Non-linear frequency in channels
Eye patterns
An eye diagram or eye pattern is simply a graphical display of a serial data signal with respect to time that shows a pattern that resembles an eye.
The signal at the receiving end of the serial link is connected to an oscilloscope and the sweep rate is set so that one- or two-bit time periods (unit intervals or UI) are displayed. This causes bit periods to overlap and the eye pattern to form around the upper and lower signal levels and the rise and fall times. The eye pattern readily shows the rise and fall time lengthening and rounding as well as the horizontal jitter variation.

Fig 9: Eye diagram
Equalization
For reliable communication, we need to have a quality output. The transmission losses of the channel and other factors affecting the quality of the signal. The most occurring loss, as we have discussed, is the ISI.
To make the signal free from ISI, and to ensure a maximum signal to noise ratio, we need to implement a method called Equalization.
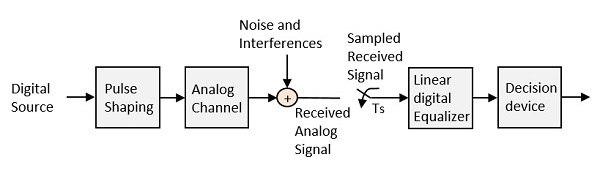
Fig 10: Equalization
The noise and interferences which are denoted in the figure, are likely to occur, during transmission. The regenerative repeater has an equalizer circuit, which compensates the transmission losses by shaping the circuit. The Equalizer is feasible to get implemented.
Key takeaway
To make the signal free from ISI, and to ensure a maximum signal to noise ratio, we need to implement a method called Equalization.
- The Orthogonal Frequency Division Multiplexing (OFDM) transmission scheme is the optimum version of the multicarrier transmission scheme. In the past, as well as in the present, the OFDM is referred in the literature Multi-carrier, Multi-tone and Fourier Transform.
- In mid-1960 parallel data transmission and frequency multiplexing came. In high-speed digital communication OFMD is employed. OFMD has a drawback of massive complex computation and high-speed memory which are no more problems now due to introduction of DSP and VLSI.
- The implementation of this technology is cost effective as FFT eliminates array of sinusoidal generators and coherent demodulation required in parallel data systems· The data to be transmitted is spread over large number of carriers. Each of them is then modulated at low rates. By choosing proper frequency between them the carriers are made orthogonal to each other.
- In OFDM the spectral overlapping among the sun carrier is allowed, at the receiver due to orthogonality the subcarriers can be separated. This provides better spectral efficiency and use to steep BPF is eliminated.
- The problems arising in single carrier scheme are eliminated in OFDM transmission system. It has the advantage of spreading out a frequency selective fade over many symbols. This effectively randomizes burst errors caused by fading or impulse interference so that instead of several adjacent symbols being completely destroyed, many symbols are only slightly distorted.
- Because of this reconstruction of majority of them even without forward error correction is possible. As the entire bandwidth is divided into many narrow bandwidths, the sub and become smaller than the coherent bandwidth of the channel which makes the frequency response over individual sub bands is relatively flat. Hence, equalization becomes much easier than in single carrier system and it can be avoided altogether if differential encoding is employed.
- The orthogonality of sub channels in OFDM can be maintained and individual subchannels can be completely separated by the FFT at the receiver when there are no inter symbol interference (ISI) and intercarrier interference (ICI) introduced by the transmission channel distortion.
- Since the spectra of an OFDM signal is not strictly band limited, linear distortions such as multipath propagation causes each subchannel to spread energy into the adjacent channels and consequently cause ISI.
- One way to prevent ISI is to create a cyclically extended guard interval, where each OFDM symbol is preceded by a periodic extension of the signal itself. When the guard interval is longer than the channel impulse response or multipath delay, the ISI can be eliminated.
- By using time and frequency diversity, OFDM provides a means to transmit data in a frequency selective channel. However, it does not suppress fading itself. Depending on their position in the frequency domain, individual subchannels could be affected by fading.
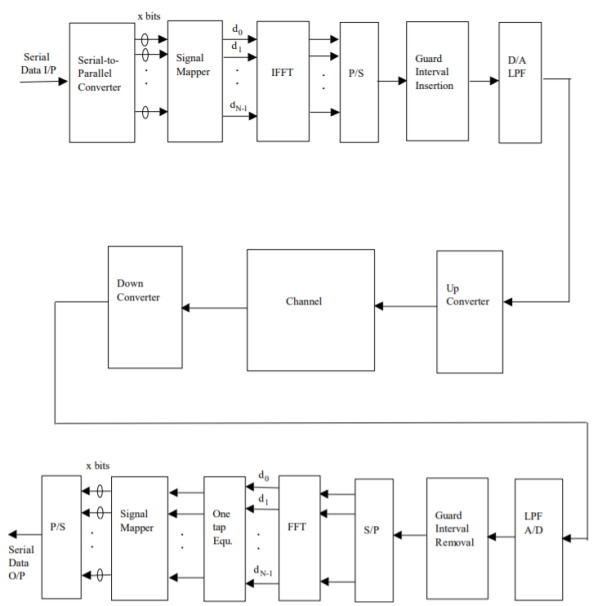
Fig 11: General OFDM System
The incoming signal is converted to parallel form by serial to parallel converter. After that it is grouped in x bits to form a complex number. These numbers are then modulated in a baseband manner by IFFT. Then through parallel to serial converted they are converted to serial data and transmitted. In order to avoid inter symbol interference a guard interval is inserted between the symbols. The discrete symbols are converted to analog and lowpass filtered for RF up-conversion. The receiver performs the inverse process of the transmitter. One tap equalizer is used to correct channel distortion. The tap coefficients of the filter are calculated based on channel information.
Key takeaway
The OFDM scheme differs from traditional FDM in the following interrelated ways:
- Multiple carriers (called subcarriers) carry the information stream
- The subcarriers are orthogonal to each other.
- A guard interval is added to each symbol to minimize the channel delay spread and inter-symbol interference.
Modulation scheme |  | 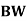 | Probability of error 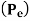 | Comments |
Coherent ASK
Non-Coherent ASK |  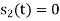 | 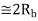 | 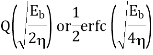 | Rarely used |
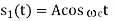 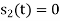 | 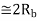 | 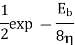 | Rarely used | |
Coherent FSK
Non-Coherent FSK |  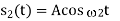 | 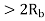 | 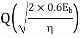 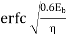 | 2.2 dB more power required than PSK Requires more Bandwidth. |
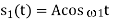 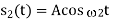 | 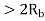 | 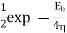 | No advantage over PSK, so seldom used | |
Coherent PSK
Non-Coherent PSK
DPSK | 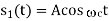 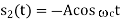 | 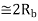 |  | 3dB power advantage over ASK |
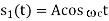  | 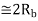 | 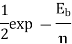 | DPSK is non-coherent version of PSK, but only little inferior than coherent PSK 1dB more power)
|
 two-sided noise PSD,
two-sided noise PSD, 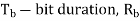 is bit rate
is bit rate
Energy 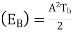 , where
, where 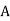 -carrier amplitude
-carrier amplitude
Case Study
QAM for Wireless Communication
Another major development occurred in 1987 when Sundberg, Wong and Steele published a pair of papers. Considering QAM for voice transmission over Rayleigh fading channels, the first major paper considering QAM for mobile radio applications. In these papers, it was recognized that when a Gray code mapping scheme was used, some of the bits constituting a symbol had different error rates from other bits. Gray coding is a method of assigning bits to be transmitted to constellation points in an optimum manner. For the 16-level constellation two classes of bits occurred, for the 64-level three classes and so on. Efficient mapping schemes for pulse code modulated (PCM) speech coding was, discussed where the most significant bits (MSBs) were mapped onto the class with the highest integrity. A number of other schemes including variable threshold systems and weighted systems were also discussed. Simulation and theoretical results were compared and found to be in reasonable agreement. They used no carrier recovery, clock recovery or AGC, assuming these to be ideal, and came to the conclusion that channel coding and post-enhancement techniques would be required to achieve acceptable performance.
This work was continued, resulting in a publication in 1990 by Hanzo, Steele and Fortune, again considering QAM for mobile radio transmission, where again a theoretical argument was used to show that with a Gray encoded square constellation, the bits encoded onto a single symbol could be split into a number of subclasses, each subclass having a different average BER. The authors then showed that the difference in BER of these different subclasses could be reduced by constellation distortion at the cost of slightly increased total BER, but was best dealt with by using different error correction powers on the different 16- QAM subclasses. A 16 kbit/s sub-band speech coder was subjected to bit sensitivity analysis and the most sensitive bits identified were mapped onto the higher integrity 16-QAM subclasses, relegating the less sensitive speech bits to the lower integrity classes. Furthermore, different error correction coding powers were considered for each class of bits to optimise performance. Again, ideal clock and carrier recovery were used, although this time the problem of automatic gain control (AGC) was addressed. It was suggested that as bandwidth became increasingly congested in mobile radio, microcells would be introduced supplying the required high SNRs with the lack of bandwidth being an incentive to use QAM.
In the meantime, CNET were still continuing their study of QAM for point-to-point applications, and detailing an improved carrier recovery system using a novel combination of phase and frequency detectors which seemed promising. However, interest was now increasing in QAM for mobile radio usage and a paper was published in 1989 by J. Chuang of Bell Labs considering NLF-QAM for mobile radio and concluding that NLF offered slight improvements over raised cosine filtering when there was mild inter symbol interference (ISI).
A technique, known as the transparent tone in band method (TTIB) was proposed by McGeehan and Bateman from Bristol University, UK, which facilitated coherent detection of the square QAM scheme over fading channels and was shown to give good performance but at the cost of an increase in spectral occupancy. At an IEE colloquium on multilevel modulation techniques in March 1990 a number of papers were presented considering QAM for mobile radio and point-to-point applications. Matthews proposed the use of a pilot tone located in the centre of the frequency band for QAM transmissions over mobile channels. Huish discussed the use of QAM over fixed links, which was becoming increasingly widespread. Webb et al. Presented two papers describing the problems of square QAM constellations when used for mobile radio transmissions and introduced the star QAM constellation with its inherent robustness in fading channels.
Further QAM schemes for hostile fading channels characteristic of mobile telephony can be found in the following recent references. If Feher’s previously mentioned NLA concept cannot be applied, then power-inefficient class A or AB linear amplification has to be used, which might become an impediment in lightweight, low-consumption handsets. However, the power consumption of the low-efficiency class A amplifier is less critical than that of the digital speech and channel codecs. In many applications 16- QAM, transmitting 4 bits per symbol reduces the signalling rate by a factor of 4 and hence mitigates channel dispersion, thereby removing the need for an equaliser, while the higher SNR demand can be compensated by diversity reception.
A further important research trend is hallmarked by Cavers’ work targeted at pilot symbol assisted modulation (PSAM), where known pilot symbols are inserted in the information stream in order to allow the derivation of channel measurement information. The recovered received symbols are then used to linearly predict the channel’s attenuation and phase. A range of advanced QAM modems have also been proposed by Japanese researchers doing cutting-edge research in the field.
References:
1. Bernard Sklar, Prabitra Kumar Ray, “Digital Communications Fundamentals and Applications”, Pearson Education, 2nd Edition
2. Wayne Tomasi, “Electronic Communications System”, Pearson Education, 5th Edition
3. A.B Carlson, P B Crully, J C Rutledge, “Communication Systems”, Tata McGraw Hill Publication, 5th Edition
4. Simon Haykin, “Communication Systems”, John Wiley & Sons, 4th Edition
5. Simon Haykin, “Digital Communication Systems”, John Wiley & Sons, 4th Edition.