UNIT - 6
Design of Control System Using State Space Technique
Controllability: A control system is said to be completely controllable if it’s possible to transfer the state of system from initial state to any other required state.
[S]= [B AB AB2 AB3 ------------------- An-1B]
Kalman’s Test: A system is said to be completely controllable if determinant of matrix is not equal to zero, or the rank of the following matrix should be to ‘n’.
n---- order of the matrix.
If 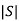 ≠0 then completely controllable
≠0 then completely controllable
If 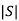 =0 then not controllable
=0 then not controllable
Question: A system is represented by following state model A= 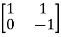 B=
B=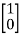 find whether it is controllable or not?
find whether it is controllable or not?
Solution: A= 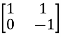 B=
B=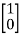
So, order of matrix is n=2
[S]=[B AB]
= 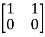
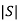 =0 hence, system is not controllable.
=0 hence, system is not controllable.
Observability: A system is said to be completely observable if it is possible to determine the initial state of system by observing the output for finite interval of time.
Calman’s Test: A system is said to be completely observable within the determinant of following matrix is not equal to zero, or, the matrix rank should be equal to 1.
[Q]= [CT ATCT (AT)2CT ----------(AT)n-1CT]
If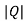 ≠0 then completely observable
≠0 then completely observable
=0 then not observable
Question: A system is represented by following state model A= 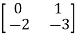 B=
B=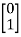 , C=[1 1] test whether the system is observable or not?
, C=[1 1] test whether the system is observable or not?
Solution: AT= 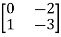 CT=
CT=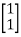
[Q]=[CT ATCT]
=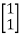
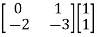
=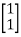
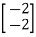
=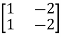
=0
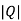 =0 hence not observable.
=0 hence not observable.
Refer section 6.1
Observable Canonical Form:
An Observable canonical form is used to analyse and design control systems because this form allows observability. A system is observable if all its states can be determined by the output. Consider a transfer function of third order
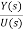 =T(s)=(b0s3+b1s2+b2s+b3)/(s3+a1s2+a2s+a3)
=T(s)=(b0s3+b1s2+b2s+b3)/(s3+a1s2+a2s+a3)
T(s)=(b0+b1/s+b2s2+b3/s3)/[1-(-a1/s-a2/s2-a3/s3)] …………(1)
By Mason’s Gain Formula
T=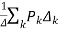 …………(2)
…………(2)
Pk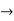 forward path transmittance of k+n path from a specified i/p node to n o/p nodes
forward path transmittance of k+n path from a specified i/p node to n o/p nodes
While calculating ipnode to n o/p nodes.
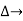 it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
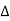 = 1- [sum of all individual loop transmitting]
= 1- [sum of all individual loop transmitting]
+[ sum of loop transmittance product of all possible non- touching loops]
-[sum of loop transmittance of all possible triples of non- touching loops]
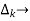 path factor associated with concered path & involves all a in the graphic which are isolated from forward path under consideration.
path factor associated with concered path & involves all a in the graphic which are isolated from forward path under consideration.
The path factor 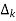 for kthis equal to graph determinant of SFG which effect after erasing the kth path from the graph.
for kthis equal to graph determinant of SFG which effect after erasing the kth path from the graph.
The required SFG is shown below, we can conclude
y=x1+b0u
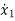 =-a1(x1+b0u)+x2+b1u
=-a1(x1+b0u)+x2+b1u
=-a1x1+x2+(b1-a1b0)u ……….(3)
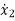 =-a2x1+x3+(b2-a2b0)u ……….(4)
=-a2x1+x3+(b2-a2b0)u ……….(4)
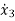 =-a3x1+(b3-a3b0)u …………(5)
=-a3x1+(b3-a3b0)u …………(5)
y=[1 0 0] +b0u ………….(6)
+b0u ………….(6)
The resulting matrix is given below
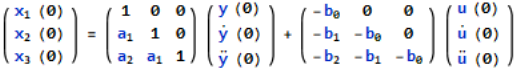
The above equations in matrix form can be easily interpreted through the signal flow graph. From the equation (3) and (5) we can say that
a) There are three feedback loops touching each other and having gain -a1/s, -a2/s2 and -a3/s3.
b) There are four forward paths touching the loop and having gain b0, b1/s, b2/s2, b3/s3.
So, the signal flow graph is shown below
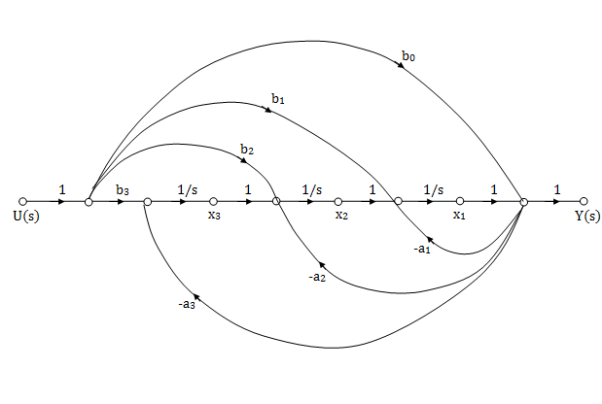
Fig: SFG for observable Form
Question: Find the observable canonical realization of the system H(s)=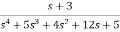
Solution: The above transfer function can be also written as
H(s)=
Comparing above equation with standard equation we conclude that
The gains of forward paths are 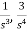
The feedback loop gains are 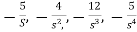
The SFG satisfying above conditions will be
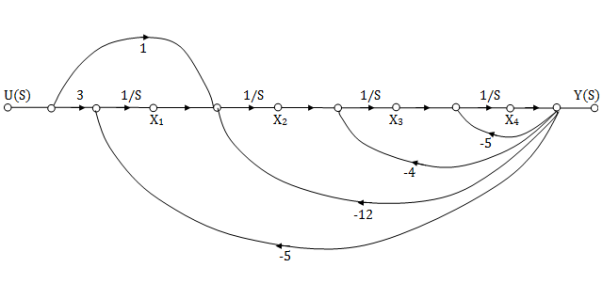
The observable canonical form can be obtained by converting the above SFG to block diagram
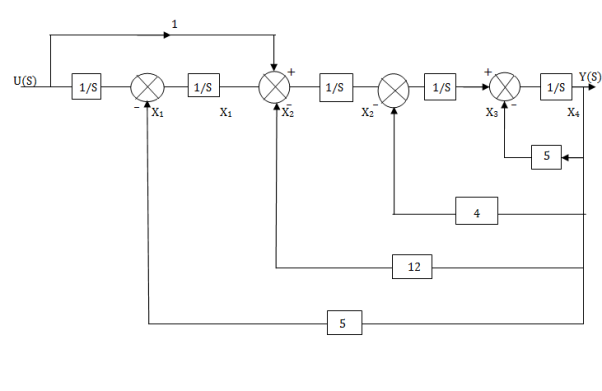
Controllable Canonical Form: In this the transfer function is divided into two parts as shown in below figure.
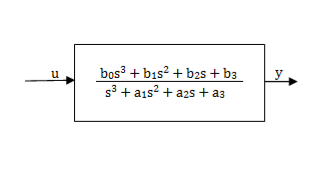
Fig: A third order system
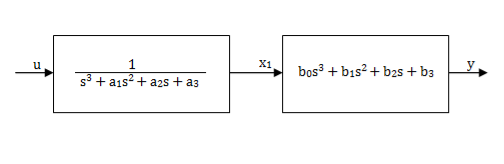
Fig: Simplified representation of above system
G(s)=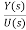 =
= 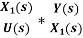
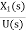 =
=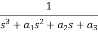 ………..(7)
………..(7)
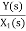 =b0s3+b1s2+b2s+b3
=b0s3+b1s2+b2s+b3
The equation relating phase variable to input is given as

The equation relating output to phase variable can be given as(refer eq.(7))
y=b0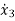 +b1
+b1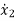 +b1
+b1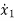 +b3x1
+b3x1
=b0(-a3x1-a2x2-a1x3+u)+b1x3+b2x2+b3x1
=(b3-a3b0)x1+(b2-a2b0)x2+(b1-a1b0)x3+b0u
The above equation in vector matrix form can be written as
y=[((b3-a3b0) (b2-a2b0) (b1-a1b0)]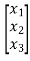 +b0u ……..(8)
+b0u ……..(8)
The signal flow graph for above vector matrix equations is shown below
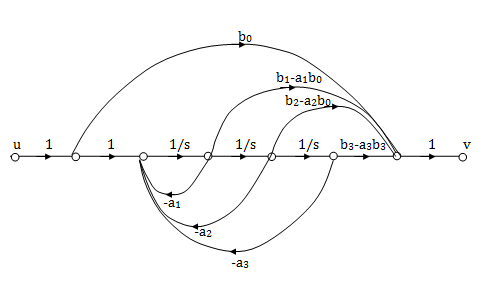
Fig: SFG for controllable form
Question: Find the controllable canonical realization of the following systems
a) H(s)=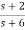
b) H(s)=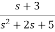
Solution: a) H(s)=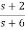
Let H(s)=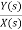
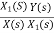 =
=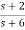
H1(s)=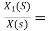 1/s+6
1/s+6
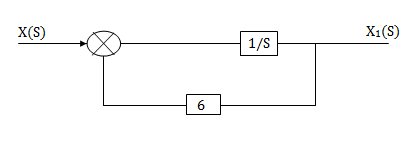
X(s)=sX1(s)+6X1(s)
SX1(s)= X(s) +6X1(s)
We can get X1(s) by passing sX1(s) through integrator. The above equation can be realised as
H2(s)=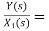 s+2
s+2
Similarly, Y(s)= sX1(s)+2X1(s)
H2(s)=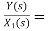 s+2
s+2
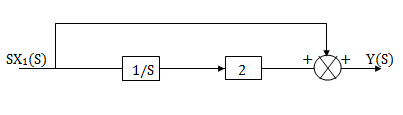
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
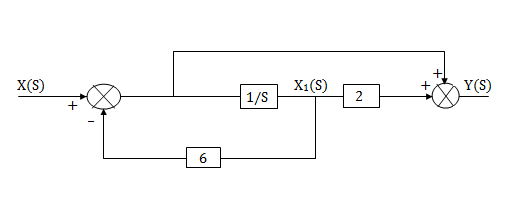
b)H(s)=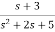
Let H(s)=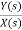 =
= 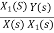
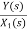 =s+3
=s+3
Y(s)=sX1(s)+3X1(s)
The above transfer function can be realised as
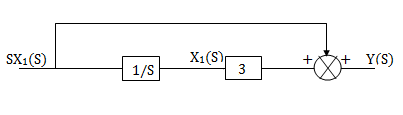
Now, 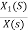 =
=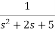
s2X1(s)=X(s)-2sX1(s)-5X1(s)
Assuming s2X1(s) is available the above transfer function can be realised as
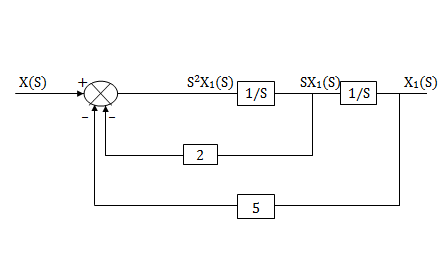
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
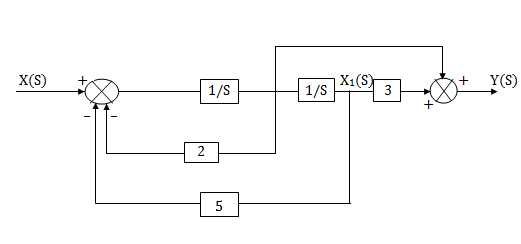
Q1) The closed loop transfer function is given as T(s)=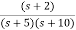 . Calculate the state model?
. Calculate the state model?
Sol: The transfer function can be simplified using partial fraction method as
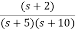 =
=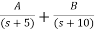
S+2=As+10A+Bs+5B
Equating coefficients of s from both sides
A+B=1
Equating coefficients of s0 from both sides
10A+5B=2
Solving above equations we get
A=-3/5
B=8/5
The transfer function will be
T(s)=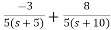
=-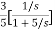 +
+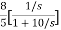
Number of poles= Number of energy storing elements
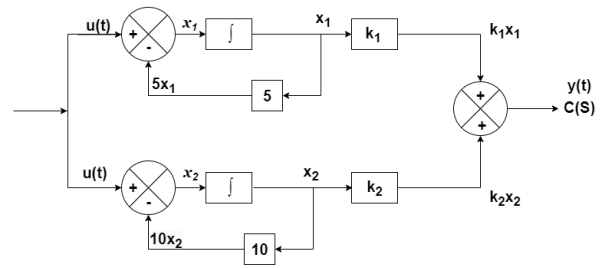
The output equation is given as
y(t)=k1x1(t)+k2x2(t)
y(t)= [k1 k2] + [0] [u(t)]
+ [0] [u(t)]
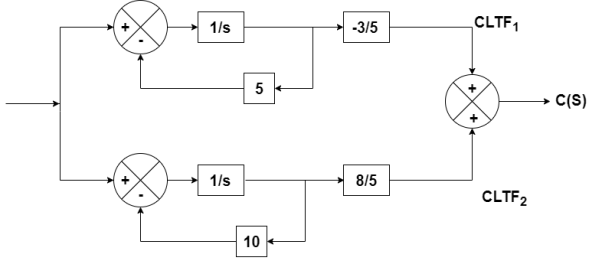
y(t)= [-3/5 8/5]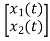 + [0] [u(t)]
+ [0] [u(t)]
C=[-3/5 8/5]
D=0
From the above block diagram
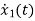 =u(t)-5 x1
=u(t)-5 x1
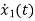 =-5x1+u(t)
=-5x1+u(t)
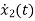 =-10x2+u
=-10x2+u
Therefore, the state equation is given as
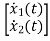 =
=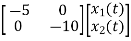 +
+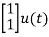
A=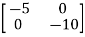
B=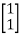
Q2) The closed loop transfer function is given as T(s)=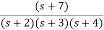 . Calculate the state model?
. Calculate the state model?
Sol: The transfer function can be simplified using partial fraction method as
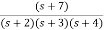 =
=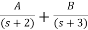 +
+ 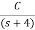
s+7=A[s2+7s+12] +B[s2+6s+8] +C[s2+5s+6]
Equating coefficients of s2 from both sides
A+B+C=0
Equating coefficients of s from both sides
7A+6B+5C=1
Equating coefficients of s0 from both sides
12A+8B+6C=7
Solving above equations and finding values of A, B and C
A=5/2
B=-4
C=3/2
The transfer function will be
T(s)=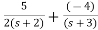 +
+ 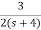
=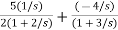 +
+ 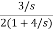
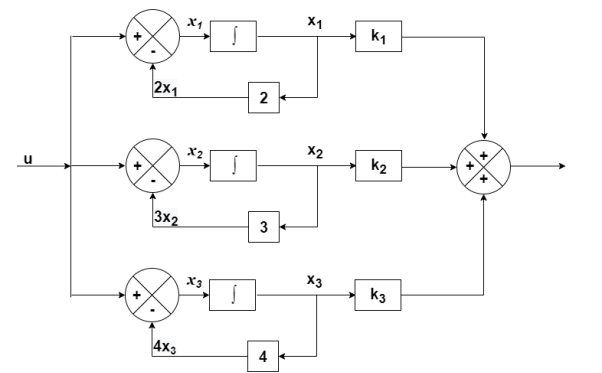
The output equation will be
y=k1x1+k2x2+k3x3
y=[k1 k2 k3]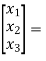 [5/2 -4 3/2]
[5/2 -4 3/2]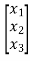
C=[5/2 -4 3/2]
D=[0]
The state equation is given as
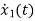 =u(t)-2x1
=u(t)-2x1
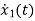 =-2x1+u(t)
=-2x1+u(t)
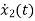 =-3x2+u
=-3x2+u
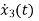 = -4x3+u
= -4x3+u
Therefore
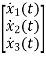 =
=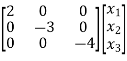 +
+ [u]
[u]
A=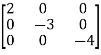
B=
Inferences from the above matrices (Jordan’s canonical form)
a) Matrix [A] is diagonal matrix and the diagonals are closed loop poles.
b) Matrix [B] is always of the form 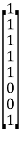
c) Matrix [C] contains residue of poles
d) Matrix [D] is always zero When number of poles ≠ number of zeros
e) When number of poles = number of zeros only change comes in matrix [D]. It is the ratio of coefficient of highest power of s in closed loop transfer function.
Q3) The closed loop transfer function is T(s)=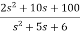 . Find the state equation?
. Find the state equation?
Sol: Here the number of poles = number of zeros
T(s)=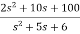
=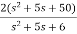
=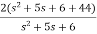
=2+ 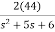
=2+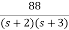
Solving above by partial fraction method
88= As+2A+Bs+3B
A=-B
2A+3B=88
A=-88
B=88
The transfer function becomes
T(s)= 2-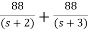
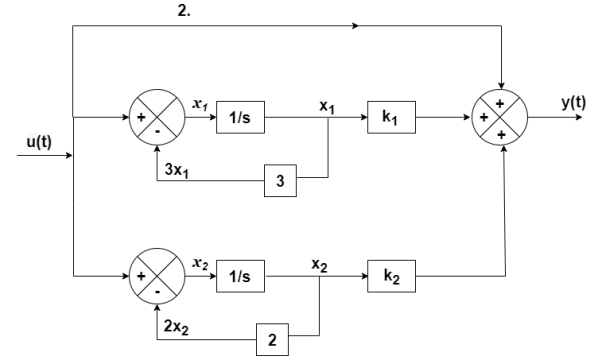
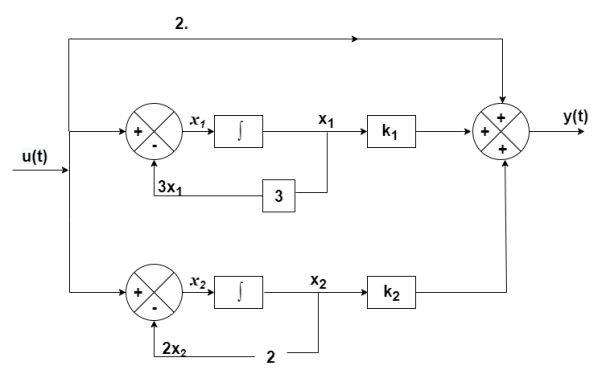
The output equation will be
y(t)=2U+k1x1+k2x2
y=[-88 88]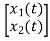 +[2]u
+[2]u
The output equation will be
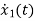 =u(t)-3 x1
=u(t)-3 x1
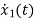 =-3x1+u(t)
=-3x1+u(t)
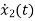 =-2x2+u(t)
=-2x2+u(t)
Therefore, the state equation is given as
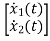 =
=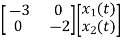 +
+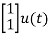
A=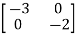
B=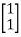
For an nth order system with distinct eigenvalues the transfer function be
T(s)=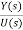 =[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an]
=[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an]
=K(s- 1)( s-
1)( s-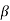 2)…….( s-
2)…….( s-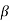 m)/(s-
m)/(s-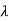 1)( s-
1)( s-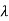 2)……( s-
2)……( s-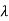 n)
n)
= 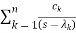
ck are residue poles at s=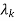
If the transfer function has identical pair of poles and zeros at 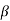 i=
i= 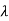 i
i
The effect of this cancellation of pole and zero on observability and controllability depends on the property of state variable.
- If the state variable is of the form below , then ci=0 will appear in control vector B and the state is uncontrollable.
 =
= 
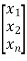 +
+  u
u
y=[1 1 1……..1]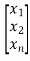 +b0u
+b0u
- On the other-hand if the state variables are of the form
 =
=  +
+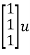
y=[c1 c2 c3…….. cn]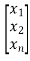 +b0u
+b0u
Then then ci=0 will appear in output vector C and the state is shielded from observations.
- In LTI system if it has pole zero cancellation, the system will either be not controllable nor observable. But if the transfer function does not have any pole zero cancellations than the system can be represented by completely controllable and observable state model.
The duality between the controllability and observability is shown. Consider system S1 shown below
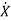 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
y=Cx
Then the dual system S2 is defined as
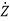 =A*z + C*v
=A*z + C*v
n= B*z
A*=conjugate transpose of A
B*= conjugate transpose of B
C*= conjugate transpose of C
The principle of duality states that system S1 is completely state controllable (observable) if and only if system S2 is completely observable (state controllable).
- For system S1
The condition for state controllability is given as
[B AB AB2 AB3 ------------------- An-1B]
The necessary condition for complete observability is given as
[CT ATCT (AT)2CT ----------(AT)n-1CT]
- For system S2
The condition for state controllability is given as
[CT ATCT ATCT2 AT CT3 ------------------- AT(n-1) CT]
The necessary condition for complete observability is given as
[B AB AB2 AB3 ------------------- An-1B]
The state-space design method is based on the pole-placement method and the quadratic optimal regulator method. The pole placement method is similar to the root-locus method. In that we place closed-loop poles at desired locations. The basic difference is that in the root-locus design we place only the dominant closed loop poles at the desired locations, while in the pole-placement method we place all closed-loop poles at desired locations. The state variable feedback may be used to achieve the desired pole locations of the closed-loop transfer function. The approach is based on the feedback of all the state variables, and therefore u = Kx. When using this state variable feedback, the roots of the characteristic equation are placed where the transient performance meets the desired response.
The nth order state model is given as
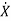 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
y=Cx
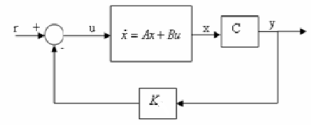
Fig: State variable feedback system
The state variable feedback is given as
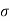 =Kx = [k1 k2 ……….kn]
=Kx = [k1 k2 ……….kn]
The block diagram is shown above. From above figure we can write
u = -Kx+r
Where u = Plant input and r = system input
The necessary condition for pole placement is that the system should be completely controllable.
Design steps of pole placement:
- Check the controllability condition for the system. If system is completely controllable then proceed to next step.
- Determine a1,a2 …. an from matrix A using characteristic equation |
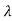 I-A|= sn+a1sn-1+…..+an-1s+an
I-A|= sn+a1sn-1+…..+an-1s+an - Determine transformation matrix T. By T=QW
Where Q=controllability matrix
W=
4. From the eigenvalues 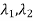 …….
…….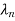 determine the characteristic polynomial (s-
determine the characteristic polynomial (s-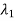 )(s-
)(s-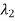 )….(s-
)….(s-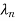 )= sn+α1sn-1+…..+ α n-1s+ αn. Then determine α1 ,α2,……. αn
)= sn+α1sn-1+…..+ α n-1s+ αn. Then determine α1 ,α2,……. αn
5. Determine the state feedback matrix K , which is given as
K=[ αn- an αn-1 an-1 ………….. α2 – a2 α1- a1]T-1
An observer is a dynamic system that is used to estimate the state of a system or some of the states of a system. A full-state observer is used to estimate all the states of the system. The observer can be designed as either a continuous-time system or a discrete-time system. The characteristics are the same, and the design processes are at least very similar and, in some cases, identical. These notes will focus primarily on continuous-time observers.
The purpose of the observer is to generate an estimate of the state x(t) based on measurements of the system output y(t) and the system input u(t). The observer is an nth-order linear dynamic system, where n is the number of state variables in the system.
Consider the system defined by
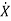 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
y=Cx
But for a completely observable system the transformation matrix Q is given as
Q=(WN*)-1
N= [C* A*C* (A*)2C* ----------(A*)n-1C*]
A*=conjugate transpose of A
C*= conjugate transpose of C
W=
Where 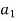
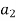 …….
…….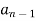 are coefficients of original state equation
are coefficients of original state equation
|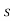 I-A|= sn+a1sn-1+…..+an-1s+an
I-A|= sn+a1sn-1+…..+an-1s+an
Let us consider a new state variable as x=Q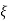
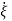 =Q-1AQ
=Q-1AQ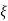 +Q-1Bu
+Q-1Bu
y=CQ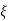
Q-1AQ=
Q-1B=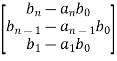
CQ=[0 0 0 …….0 1]
Let the state observer dynamics be
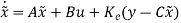
=(A-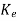 C)
C)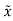 + Bu+
+ Bu+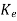 Cx
Cx
Now, 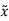 =Q
=Q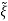
Substituting value of 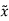 in
in 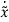 we get
we get
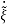 =Q-1((A-
=Q-1((A-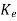 C) Q
C) Q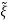 +Q-1Bu+Q-1
+Q-1Bu+Q-1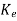 CQ
CQ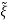
But we also know
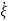 =Q-1AQ
=Q-1AQ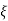 +Q-1Bu
+Q-1Bu
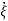 -
-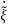 = Q-1((A-
= Q-1((A-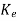 C) Q(
C) Q(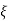 -
-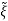 )
)
Let 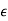 =
=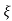 -
-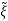
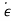 = Q-1(A-
= Q-1(A-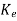 C) Q
C) Q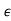
The main requirement here is to make error dynamics asymptotically stable and 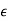 (t) should reach zero. For determining
(t) should reach zero. For determining 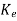 we first select the desired observer poles which are the eigenvalues of A-
we first select the desired observer poles which are the eigenvalues of A-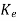 C and then finding
C and then finding 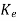 .
.
We also know Q-1=WN*
Q-1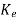 =
=
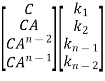
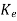 =
= 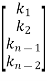
Q-1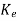 can also be written as
can also be written as
Q-1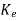 =
=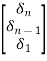
But CQ=[0 0 0……….1]
Q-1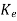 CQ=
CQ= 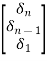 [0 0 0……….1]=
[0 0 0……….1]=
The characteristic equation is given as
|sI- Q-1(A-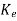 C) Q|=0
C) Q|=0
sn+(a1+ 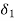 )sn-1+(a2+
)sn-1+(a2+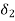 )sn-2+……+(an+
)sn-2+……+(an+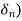 =0
=0
Let the desired characteristics equation for the error dynamics be
(s-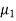 )(s-
)(s-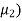 ………(s-
………(s-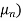 = sn+(
= sn+(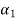 )sn-1+(
)sn-1+(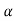 2)sn-2+……+(
2)sn-2+……+(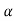 n
n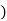 =0
=0
a1+ 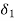 =
=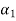
.
.
.
an+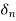 =
=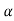 n
n
Hence Q-1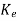 =
=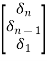 =
=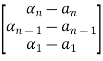
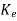 =Q
=Q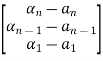
=(WN*)-1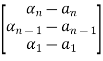
Once the desired eigenvalues are selected the full order state observer can be designed, provided the system is completely observable.
Q) Consider a system 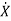 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
y=Cx
Where A=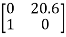 B=
B=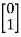 C=[0 1]. Design a full order stet observer, assuming that eigenvalues of the observer matrix are
C=[0 1]. Design a full order stet observer, assuming that eigenvalues of the observer matrix are 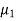 =-1.8+j2.4 and
=-1.8+j2.4 and 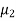 =-1.8-j2.4?
=-1.8-j2.4?
Sol: The characteristic equation of the system is given as
|sI-A|=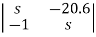 =s2-20.6=s2+a1s+a2=0
=s2-20.6=s2+a1s+a2=0
a1=0
a2=-20.6
The desired characteristic equation is given as
(s-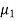 )(s-
)(s-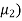 ………(s-
………(s-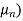 =(s+1.8+j2.4)(s+1.8-j2.4)= s2+3.6s+9=s2+a1s+a2=0
=(s+1.8+j2.4)(s+1.8-j2.4)= s2+3.6s+9=s2+a1s+a2=0
a1=3.6
a2=9
The observer gain matrix 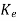 is given as
is given as
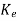 =(WN*)-1
=(WN*)-1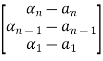
For above case we can write
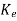 =(WN*)-1
=(WN*)-1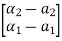 =
=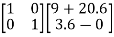 =
=