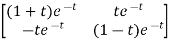UNIT - 5
Solution of State Equations
Diagonalization
A diagonal system matrix has an advantage that each state equation is the function of only one state variable. Hence, each state equation can be solved simultaneously. The technique of transforming a non-diagonal matrix to diagonal matrix is known as diagonalization.
The state equation is given as
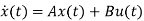
Y(t)=Cx(t)+Du(t)
Let the eigen values of matrix A be 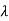 1,
1,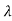 2,
2,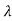 3 …… Then Let us transform X into a new state vector Z
3 …… Then Let us transform X into a new state vector Z
X=PZ
P is n x m non-singular matrix
P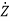 =APZ+BU
=APZ+BU
Y=CPZ+DU
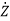 =
=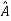 Z+
Z+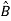 U
U
Y=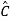 Z+
Z+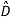 U
U
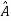 =P-1AP
=P-1AP
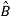 = P-1B
= P-1B
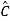 =CP
=CP
Eigenvalues
Let the transfer function be
T(s)=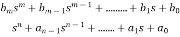
The characteristic equation is
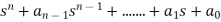 =0
=0
But we already know
SX(s)-X(0)=AX(s)+BU(s)
(sI-A)X(s)=X(0)+BU(s)
X(s)= (sI-A)-1X(0)+ (sI-A)-1BU(s)
Y(s)=C(sI-A)-1X(0)+C(sI-A)-1BU(s)+DU(s)
For zero initial conditions
Y(s)= C(sI-A)-1BU(s)+DU(s)
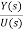 = C{[SI-A]-1B} + D
= C{[SI-A]-1B} + D
[SI-A]-1=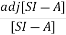
The denominator of above equation is the characteristic equation
[SI-A]=0
As the eigen values of matrix A be 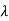 1,
1,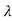 2,
2,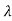 3 ……then
3 ……then
|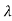 iI-A|=0
iI-A|=0
Eigenvectors
Any non-zero vector Xi satisfies
|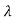 iI-A| Xi =0
iI-A| Xi =0
Xi=|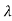 iI-A|-1. 0
iI-A|-1. 0
=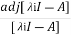 . 0
. 0
But Xi is non-zero so, solution exists if |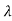 iI-A|=0 from which eigen values can be determined.
iI-A|=0 from which eigen values can be determined.
 Let Xi=mi. The solution mi is called as the eigenvector of A associated with eigen valued
Let Xi=mi. The solution mi is called as the eigenvector of A associated with eigen valued 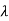 i. Let m1,m2,m3…. Be the eigenvectors corresponding to the eigenvalues
i. Let m1,m2,m3…. Be the eigenvectors corresponding to the eigenvalues 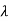 1,
1,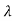 2,
2,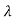 3…..respectively. Then the matrix formed by placing the eigenvectors together is known as model matrix P of A. This matrix is also known as diagonalizing matrix.
3…..respectively. Then the matrix formed by placing the eigenvectors together is known as model matrix P of A. This matrix is also known as diagonalizing matrix.
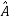 =P-1AP
=P-1AP
When A=
The model matrix is given as V= 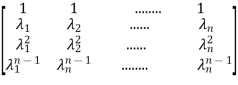
The above matrix is called as Vander Monde Matrix.
Q1) Find the eigenvectors of the matrix A= 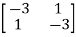
Sol: For eigenvalues |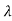 iI-A|=0
iI-A|=0
|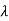 I-A|=
I-A|=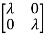 -
- 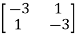 =0
=0
|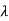 I-A| =
I-A| = 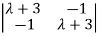 =0
=0
|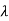 I-A| = (
I-A| = (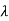 +3)2-1=0
+3)2-1=0
|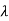 I-A| =
I-A| =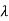 2+6
2+6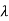 +8=0
+8=0
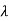 1=-2,
1=-2, 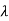 2=-4
2=-4
For 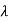 1=-2 the eigenvectors are
1=-2 the eigenvectors are
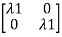 -
- 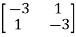 x Xi=0
x Xi=0
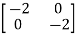 -
- 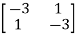 x
x  = 0
= 0
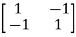
 = 0
= 0
-x1+x2=0
For x1=1 x2=1 the equation above is satisfied.
Xi=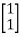
For 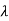 2=-4
2=-4
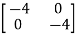 -
- 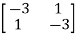 x
x  = 0
= 0
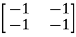
 = 0
= 0
-x1-x2=0
For x1=1 x2= -1 the equation above is satisfied.
Xi=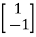
Q2) For the given matrix A=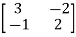
Sol: For eigen values
|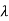 I-A|=
I-A|=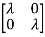 -
- 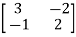 =0
=0
|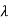 I-A| =
I-A| = 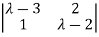 =0
=0
|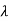 I-A| = (
I-A| = (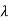 -3)(
-3)(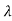 -2)-2=0
-2)-2=0
|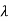 I-A| =
I-A| =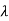 2-5
2-5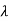 +4=0
+4=0
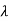 1=1,
1=1, 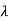 2=4
2=4
For 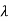 1=1 the eigenvectors are
1=1 the eigenvectors are
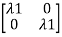 -
- 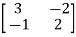 x Xi=0
x Xi=0
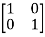 -
- 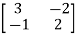 x
x  = 0
= 0
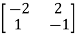
 = 0
= 0
-2x1+2x2=0
For x1=1 x2=1 the equation above is satisfied.
X1=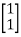
For 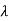 2=4
2=4
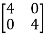 -
- 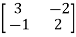 x
x  = 0
= 0
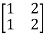
 = 0
= 0
x1+2x2=0
For x1=2 x2= -1 the equation above is satisfied.
X2=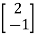
Arrange eigenvectors in a matrix P = 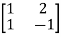
P-1= - 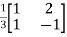 =
=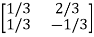
The transformation matrix 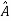 =P-1AP
=P-1AP
=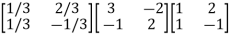
=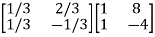
=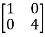
We can always diagonalize a matrix with distinct eigenvalues (whether these are real or complex). We can sometimes diagonalize a matrix with repeated eigenvalues. (The condition for this to be possible is that any eigenvalue of multiplicity m had to have associated with m linearly independent eigenvectors.) The situation with symmetric matrices is simpler. Basically, we can diagonalize any symmetric matrix. To take the discussions further we first need the concept of an orthogonal matrix. A square matrix A is said to be orthogonal if its inverse (if it exists) is equal to its transpose: A −1 = AT or, equivalently, AAT = ATA = I.
Let us understand using few examples.
EX.1 Consider a matrix A=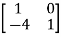
The characteristic equation is given as |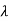 I-A|=0
I-A|=0
(1-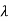 )(1-
)(1-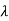 )=0
)=0
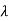 1=
1=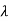 2=1, which means it has only one eigenvalue i.e. 1 which is repeated. But has a multiplicity of 2.
2=1, which means it has only one eigenvalue i.e. 1 which is repeated. But has a multiplicity of 2.
Now, finding eigenvectors of A corresponding to 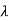 =1
=1
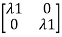 -
- 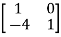 x Xi=0
x Xi=0
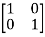 -
-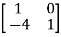 x
x  = 0
= 0
x1=x2
-4x1+x2=x2
The solution is x1=0 and x2 is any arbitrary value. The possible eigenvectors can be 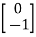 ,
, 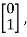
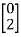 ……….
……….
Now, to form the eigenvector matrix P considering any two values of eigenvectors P=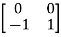
But P has zero value of determinant. Thus, P-1 does not exist and finding the transformation matrix 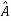 =P-1AP is also not possible. So, diagonalization of above matrix is not possible.
=P-1AP is also not possible. So, diagonalization of above matrix is not possible.
EX.2 Consider A=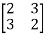
The above matrix has non-repeated eigenvalues of 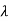 1=-1,
1=-1, 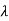 2=5 (distinct)
2=5 (distinct)
The eigenvectors corresponding to these values are X1=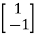 X2=
X2=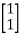
Arrange eigenvectors in a matrix P = 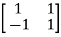 . The |P|≠0. Hence, P-1 exist and finding the transformation matrix
. The |P|≠0. Hence, P-1 exist and finding the transformation matrix 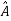 =P-1AP is also possible. So, diagonalization of above matrix is possible.
=P-1AP is also possible. So, diagonalization of above matrix is possible.
Refer Section 5.1 Eigenvectors
Solution of homogeneous state equation
The first order differential equation is given as
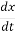 =ax x(0)=x0
=ax x(0)=x0
x(t)=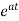 x0=
x0=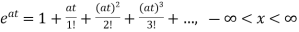
Consider state equation
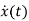 =Ax(t); x(0)=x0
=Ax(t); x(0)=x0
The solution will be of the form
x(t)=a0+a1t+a2t2+a3t3+….+aiti
Substituting value in above equation
a1+2a2t2+3a3t3+……….=A[a0+a1t+a2t2+a3t3+….+aiti]
a1=Aa0
a2= Aa1=
Aa1=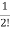 A2a0
A2a0
ai= Aia0
Aia0
Solution for x(t) will be
x(t)=[I+At+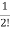 A2t2+………+
A2t2+………+ Aiti]x0
Aiti]x0
The matrix exponential form can be written as
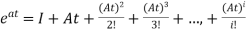
The solution x(t) will be x(t)=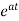 x0
x0
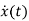 =Ax(t)+Bu(t) and x(0)=x0
=Ax(t)+Bu(t) and x(0)=x0
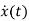 - Ax(t)=Bu(t)
- Ax(t)=Bu(t)
Multiplying both sides by 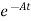
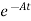 [
[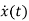 - Ax(t)]=
- Ax(t)]=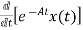 =
=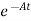 Bu(t)
Bu(t)
Integrating both sides w.r.t t we get
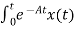 =
= 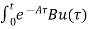 d
d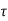
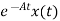 =
=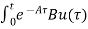 d
d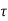
Multiplying both sides by 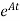
x(t)=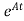 x(0)+
x(0)+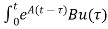 d
d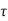
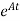 x(0) is called as Homogeneous solution
x(0) is called as Homogeneous solution
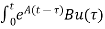 d
d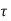 is the Forced solution
is the Forced solution
At t=t0
x(t)=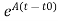 x(t0)+
x(t0)+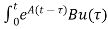 d
d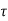
The above equation is the required solution.
Solution of non-homogeneous state equation
Let the scalar state equation be
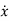 =ax+bu
=ax+bu
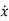 -ax=bu
-ax=bu
Multiplying both sides by e-at
x(t) = eat x(0) +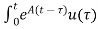 d
d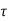
Then for non-homogeneous state equation
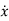 =Ax+Bu
=Ax+Bu
The solution x(t) can be given as
x(t) = eAt x(0) +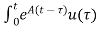 d
d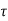
The above equation is the required solution.
State Transition Matrix and its Properties:
y(t)=Cx(t)+Du(t)
x(t)=Ax(t)+Bu(t)
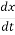 -Ax(t)=Bu(t)
-Ax(t)=Bu(t)
SX(s)-X(0)-AX(s)=BU(s)
SX(s)-AX(s)=BU(s)+X(0)
[SI-A]X(s)=X(0)+BU(s)
X(s)=[SI-A]-1[X(0)+BU(s)]
X(s)=[SI-A]-1X(0)+[SI-A]-1BU(s) (a)
This is solution of state differential equation
L-1X(s)= L-1{[SI-A]-1X(0)+[SI-A]-1BU(s)}
x(t)= [SI-A]-1x(0)+ [SI-A]-1Bu(t) (b)
From above x(t) we can find output equation by replacing x(t) in output equation by its value from above equation(b)
For the given system below
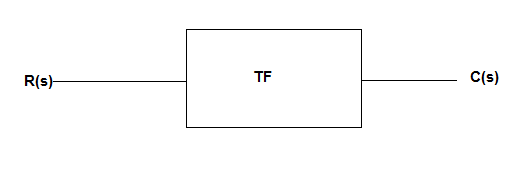
TF=c(t)/r(t)
This c(t) is output of present system, which is not equal to above y(t), as their initial conditions are not considered.
If initial conditions are zero than both y(t) and c(t) will be equal to
L-1[SI-A]-1=φ(t)…….. State transition matrix
Φ(s)=[SI-A]-1
x(t)=φ(t)x(0)+L-1[φ(s)* BU(s)] (c)
State transition matrix satisfies the solution of state equation when input is zero. [u(t)=0]
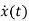 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
As u(t)=0
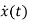 =Ax(t)
=Ax(t)
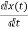 -Ax(t)=0
-Ax(t)=0
Solution to above equation is
y(t)=Ke-Pt+e-Pt∫ ePt Q d(t)
But 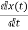 -Ax(t)=0
-Ax(t)=0
Hence above equation becomes
X(t)=AeAt
Substitute t=0
x(0)=ke0
x(0)=k
x(t)=x(0)eAt (zero input response)
Properties of state transition matrix:
From equation (31) when u(t)=0
x(t)=φ(t) x(0)
And from zero input response we have
φ(t)=eAt
Property 1:
φ(0)= [I]
Property 2:
Φ-1(t)= [φ(t)]-1=e-At=eA(-t)
Φ-1(t)= Φ(-t)
Property 3:
ΦK(t)= [Φ(t)]K
ΦK(t)=[eAt]K=eA(tK)
ΦK(t)= Φ(Kt)
Property 4:
Φ(t1+t2)=eA(t1+t2)
=e(At1+At2)=eAt1 * eAt2
Φ(t1+t2)= Φ(t1)Φ(t2)
Property 5:
Φ(t2-t1) * φ(t1-t0)=eA(t2-t1) * eA(t1-t0)
=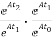
=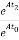 =eA(t2-t0)
=eA(t2-t0)
Φ(t2-t1) * φ(t1-t0)= Φ(t2-t0)
Question: A=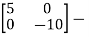 . Find the state transition matrix?
. Find the state transition matrix?
Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=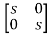
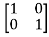 -
-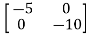
=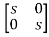 -
-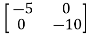
=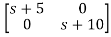
Taking inverse Laplace of above, we get
[SI-A]-1=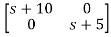 /(S+5)(S+10)
/(S+5)(S+10)
=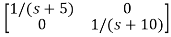
Hence φ(t)=L-1[SI-A]-1=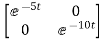
Question: Find state transition matrix if A=[SI-A]=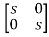
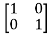 -
-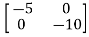
Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=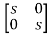 -
-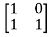
=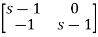
[SI-A]-1=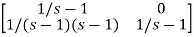
Hence φ(t)=L-1[SI-A]-1=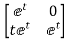
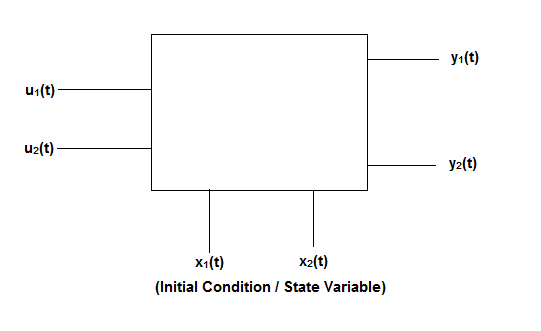
Fig: State model
The above figure shows the state model of a system with two inputs u1(t) and u2(t), and having outputs y1(t) and y2(t). As discussed in above section 5.1, we know that the output equation is given as
Y(t)=Cx(t)+Du(t) (9)
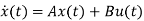 (10)
(10)
Taking L.T of equation (9)
Y(s)=CX(s)+DU(s) (11)
Taking L.T of equation (10)
SX(s)=AX(s)+BU(s) (12)
X(s)=[SI-A]-1BU(s) (13)
Y(s)=CX(s)+DU(s)
Y(s)=C{[SI-A]-1BU(s)} + DU(s)
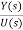 = C{[SI-A]-1B} + D (14)
= C{[SI-A]-1B} + D (14)
[SI-A]-1=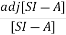
The denominator of equation (14) is the characteristic equation
[SI-A]=0
Q.1) A=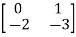 . Calculate characteristic equation and stability?
. Calculate characteristic equation and stability?
Sol: The characteristic equation is given as [SI-A]=0
S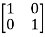 -
- 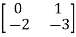 =0
=0
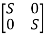 -
-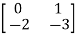 = 0
= 0
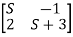 =0
=0
S(S+3)-(-1)*2=0
Hence, the characteristic equation is
S2+3S+2=0
(S+1)(S+2)=0
S=-1,-2
Both roots on left-half of s-plane, real and different, system absolutely stable.
Q.2)A= 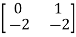 Find the characteristic equation and comment on stability?
Find the characteristic equation and comment on stability?
Sol: The characteristic equation is given by [SI-A]=0
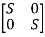 -
-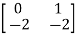 =0
=0
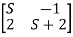 =0
=0
S(S+2)+2=0
S2+2S+2=0
S=-1±j
Roots on left-half of s-plane, complex conjugate, system absolutely stable.
According to the Cayley Hamilton theorem every square matrix A satisfies its own characteristic equation.
q(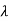 )=|
)=|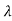 I-A|=
I-A|=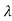 n+a1
n+a1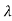 n-1+….+an-1
n-1+….+an-1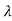 +an=0
+an=0
If above equation is the characteristic equation of A, then it should satisfy the equation
q(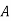 )=
)=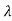 n+a1
n+a1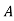 n-1+….+an-1
n-1+….+an-1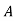 +an=0
+an=0
Let 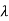 1,
1,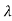 2,
2,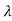 3 ….. Be the eigen values of A. Then
3 ….. Be the eigen values of A. Then
f(A)= k0I+k1A+k2A2+….+knAn+kn+1An+1…..
The matrix polynomial can be computed by the characteristic polynomial q(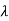 )
)
f(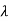 )= k0+k1
)= k0+k1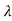 +k2
+k2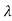 2+….+kn
2+….+kn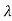 n+kn+1
n+kn+1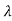 n+1…..
n+1…..
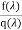 =Q(
=Q(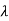 )+
)+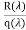
Where 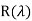 is remainder polynomial given as
is remainder polynomial given as
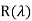 =
=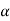 0+
0+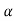 1
1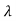 +
+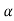 2
2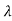 2+ ….+
2+ ….+ 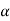 n-1
n-1 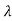 n-1
n-1
Substituting A for 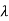
f(A)=Q(A)q(A)+R(A)
q(A) is identically zero
f(A)=R(A)
=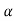 0I+
0I+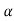 1
1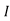 +
+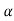 2
2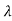 2+ ….+
2+ ….+ 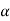 n-1
n-1 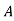 n-1
n-1
The process to find f(A) is
1) Find eigen values of matrix A
2) If all eigen values are distinct solve n simultaneous equations for 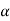 0,
0,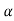 1,….,
1,….,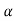 n-1
n-1
3) If A possesses an eigen value 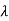 k of order m, then only one independent equation cab be obtained by differentiating both sides of equation q(
k of order m, then only one independent equation cab be obtained by differentiating both sides of equation q(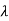 ).
).
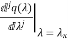 =0 j=0,1,….,m-1
=0 j=0,1,….,m-1
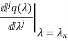 =
=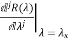 j=0,1,….,m-1
j=0,1,….,m-1
Q) Find f(A)=eAt for A=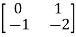
SOL: The characteristic equation is
q(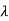 )=|
)=|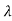 I-A|=
I-A|=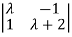 =(
=(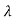 +1)2=0
+1)2=0
The eigen values of A are 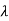 1,
1,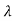 2=-1
2=-1
Since, A is of second order, R(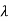 ) will be
) will be
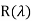 =
=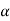 0+
0+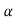 1
1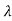
Then 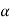 0 and
0 and 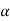 1
1
f(A)=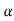 0+
0+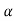 1
1
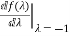 =te-t
=te-t
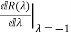 =
=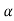 1
1
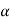 0=(1+t)e-t
0=(1+t)e-t
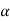 1=te-t
1=te-t
f(A)=eAt=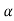 0I+
0I+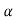 1
1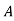
=