UNIT-4
LIGHT, COLOUR, SHADING AND HIDDEN SURFACES
Color Model
The light travels in straight line.
Light travels faster than sound.
The light reflects into our eyes hence we can see it.
Shadows are formed when light is blocked by an object.
When light is incident upon an object some are absorbed and some are reflected.
The dominant frequency decides the color of an object.
A light source is produced by a sun or electric bulb etc.
CIE stands for Commision Internationale Eclairage.
The RGB values become unpleasant when the values of RGB representation are negative.
It is defined in 1931 in base terms of virtual primary axes X, Y and Z.
This axes are used to allow to match all visible colors as linear combination with positive coefficient only.
Hence it is known as the chromaticity values X, Y, Z.
The visible colors can be expressed as the C=XX+YY+ZZ.
The normalization processed and it becomes X+Y+Z=1.
This gives new coordinates as x, y and z =1-x-y which are independent on luminous energy X+Y+Z.
The coordinates of visible chromatic value form a horseshoe shaped region with the spectrally pure colors on the curved boundary.
Following figure shows the horseshoe shape of the visible region.
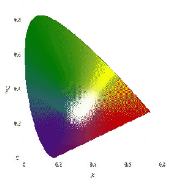
Following is the figure of CIE chromaticity.

It is color space which is commonly used.
RGB stands for Red Green Blue.
The RGB model states that the image having more colors and that colors are made up of three different images i.e red image, black image and blue image.
The grayscale image is shown by only one matrix but color image is shown by three different matrices.
One color image matrix contains: red matrix + green matrix + blue matrix
Application of RGB
It is also known as HSB (Hue Saturation Brightness)
HSV stands for Hue Saturation Value.
In HSV there are three main components are: Hue, saturation and the value.
It defines the shades and the brightness of the color.
It may be depicted as cone or cylinder.
There are secondary colors In HSV are red, yellow, green, cyan,blue and magenta.
It also having the mixture of adjacent pairs of them.
It is an alternative representation of RGB model.
The colors of each hue are arrange in radial slice.
The slices are placed around the central axis of neutral colors.
This neutral colors are ranges from the black at the bottom to white at the top.
The saturation dimension resembling various tints of brightly colored paint that colors are mix together to represent the HSV color model.
The value dimension resembling the mixture of paint is vary with the amount of black and white color.
The geometric cylinder of HSV starts with red primary at 00 passing through green primary at 120o and blue at 240o, then back to red 360o.
The geometry of central vertical axis comprises neutral, achromatic or gray colors ranging from top to bottom.
The range starts from the white at lightness 1 to black at lightness 0.
Following is the figure of HSV.

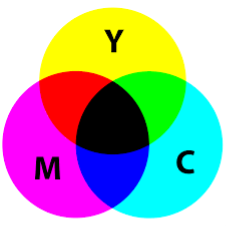
The CMY color model is a subtractive color model.
The CMY color model named from three colors as Cyan Magenta Yellow.
It contains the cyan, magenta and yellow color.
Thus main colors are used to reproduce various colors of array.
Thus are the primary color but this is not used to specify as absolute because of CMY does not meant by cyan, magenta and yellow mixture.
When the cyan, yellow and magenta becomes exact chromaticities of color then it can be specified as absolute color space.
The mixture of subtracted dyes of wavelength from the spectral power distribution of the illuminating light.
The illuminating light which scatters back into the viewer’s eyes and perceives as colors.
Following figure shows the CMY color model.
It is also called as lighting model or shading model.
It is used to calculate the intensity of light which is reflected at the given point on surface.
The lighting effects are depend on three factors:
Light source: the light sources can be point source, parallel source, distributed source etc.
Surface: the light falls on the surface part and reflects.
Observer: the position of the observer and the sensor spectrum sensitivities that also effects the light.
Following are the illumination models.
4.6.1 Ambient Light
This also referred to available lighting in an environment.
Suppose the observer is standing on the road facing the building with exterior of glass and the sun rays are falling on building reflecting back from it and falling on the object under observation.
This is known as ambient illumination.
Where the source of light is indirect then it is referred as ambient illumination.
The reflected intensity Iamb =Ka * Ia
Where Ka is the surface ambient reflectivity value which varies from 0 to 1, Ia is the ambient light intensity.
4.6.2 Diffuse Reflection
The diffuse reflection is the reflection of the rays that are scattered in many angles from the surface.
In the specular reflection the ray incident on the surface is scattered at one angle only.
The surface of the reflection should have equal luminance when viewed from all direction lying in the half space adjacent to the surface.
The surface can be plaster or fibers as paper, polycrystalline material.
The surface of reflection in diffuse reflection is rough or grainy.
The light source and the surface made angle that shows the brightness of a point.
The reflected intensity Idiff of a point on the surface:
Idiff = Kd * Ip cos(Ꙫ) = Kd * Ip (N * L)
Where Ip is the point light intensity, Kd is the surface diffuse reflectivity value, N is the surface normal and L is the light direction.
Following figure shows the diffuse and specular reflection from the glossy surface.
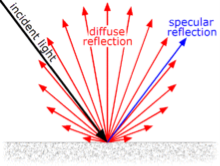
4.6.3 Specular Reflection
It is a regular reflection.
The specular reflection of light reflects from the surface like mirror reflection.
The specular reflection contrasted the diffuse reflection.
In specular reflection the light is scattered from the surface in the range of the direction.
Following figure shows the coplanar condition of the specular reflection.

4.6.4 Phong Model
It is an empirical model for specular reflection.
It is also reffered as phong illumination or phong lighting.
It is also known as the phong shading in 3D graphics.
The formula for the calculation of the reflected intensity I spec.
Ispec=W(Ꙫ) I * cos n (ф)
Where W(Ꙫ) is Ks, L is the light source, N is the normal surface, R is the direction of reflected ray, V is the direction of observer, Ꙫ be the angle between L and R, ф be the angle between R and V.
4.6.5 Combined Diffuse And Specular Reflections With Multiple Light Source
For a single point light source, the combined diffuse and the specular reflection from the point on an illuminated surface as,
I=Idiff + Ispec
= Ka . Ia + Kd . I (N . L) + Kc . I (N . H)
If we place the more than one point source then we obtain the light reflection at any surface point by summing the contribution from the individual sources.
4.6.6 Warn Model
The warn model is a method that used to simulate the lighting effects of studio by controlling light intensity in different direction.
The phong model is used for sourcing the light which reflects on the surface.
The intensity is calculate by collecting the different directional selected values of the phong exponent.
The warn model is used in light controlling, spotlighting and also used by photographers to simulation of light.
The light of source is controlled by flaps.
It is an implementation of the illumination model at the pixel points or polygon surfaces.
It is used to display colors in graphics and also used to compute the intensities.
It has two important ingredients as properties of the surface and properties of the illumination falling on it.
In intensity computation the object illumination is the most significant thing.
The diffuse illumination is the illumination which has the uniformly reflection from all the direction.
The shading models are used to determine the shade of a point on the surface of an object in terms of number of attributes.
Following figure shows the energy comes out from the point on a surface.
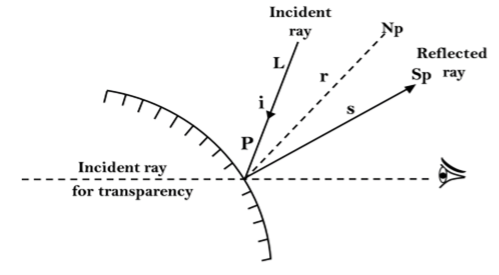
4.7.1 Halftone Algorithm
It is reprographic shading technique.
It is used to simulate continues tone imagery through dots.
The dots varies in the size or in spacing.
Hence the dots represents the gradient like effect.
Halftone is used to refer the image that is produced by this process.
The range of color in continuous tone goes to infinite or in the range of gray.
It reduces the visual reproduction of the image.
The image that is reducing can be printed with only one color of ink or dot can be differs in size or spacing.
The reproduction relies on the optical illusion.
The halftone dots are so small that human eyes interprets it the patterned areas if they were smooth tones.
Following is the halftone dots and human eye interpretation.

4.7.2 Gauraud Algorithm
It is also known as gouraud shading when it renders a polygon surface by linear interpolating intensity value across the surface.
It is an intensity interpolation scheme.
The intensity values for each polygon are coordinates with the value of adjacent polygon along the common edges.
Hence eliminating the intensities discontinuities happens like flat shading.
Following are some calculations that are occurred in gauraud shading.
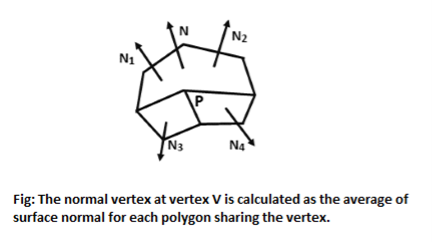
Determining average unit normal vector at each polygon vertex
Apply an illumination model to each vertex to determine the vertex intensity
Linear interpolate the vertex intensities over the surface of the polygon.
The normal vector obtain by averaging the surface normals of all polygons staring that vertex from each polygon vertex.
Following figure shows the gauraud shading.
4.7.3 Phong Shading
It is a more accurate method to render a polygon surface.
The polygon surface that interpolates the normal vertex and then apply the illumination model to each surface point.
This method is also known as the normal vector interpolation shading.
It is used to display more realistic highlights on the surface.
It is also use to reduce the match band effect.
Following are the steps to render a polygon surface using phong shading:
Following figure shows the phone shading between two vertices.
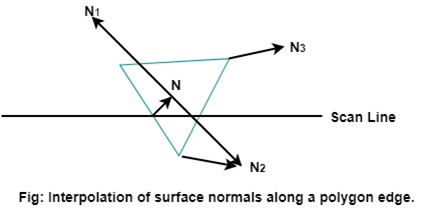
The evaluation of normal between the scam lines are determined by the incremental method along with each scan line.
The illumination model is applied on each of the scan line to determine the surface intensity at that point.
The accurate result is produced by the intensity calculation using approximated normal vector at each point along the scan line instead of using the direct interpolation of intensities.
The phone shading requires more calculations than other shading algorithms.
The hidden surface is used to remove the parts from the image of solid objects.
The hidden surface is disable by using opaque material which obstructs the hidden parts and prevents us from seeing them.
The automatic elimination does not happens when the objects are projected onto the screen coordinate system.
To remove some part of surface or object we need to apply a hidden line or hidden surface algorithm to such objects.
The algorithm operates on the different kinds of models.
The model will generate various forms of output or different complexities in images.
The geometric sorting algorithms are used for distinguishing the visible parts and invisible parts.
Hidden surface algorithm is generally used to exploit one or many of coherence properties to increase efficiency.
Following are the algorithms that are used for hidden line surface detection.
It is simple and straight forward method.
It reduces the size of databases, as only front or visible surfaces are stored.
The area that is facing the camera is only visible in back face removal algorithm.
The objects on the back side are not visible.
The 50% of polygons are removed in this algorithm when it uses parallel projection.
When perspective projection is used then more than 50% of polygons are removed.
If the objects are nearer the center of projection then number of polygons are removed.
It is applied on the individual objects.
It does not consider the interaction between various objects.
Many polygons are captured by front face as they are closer to the viewer.
Hence for removing such faces back face removal algorithm is used.
When the projection takes place, there are two surfaces one is visible front surface and the other is not visible back surface.
Following is the mathematical representation of back face removal algorithm.
N1=(V2 - V1) (V3 - V2)
If N1 * P >= 0 visible and N1 * P < 0
It is also called as Z – buffer algorithm.
It is a simplest image space algorithm.
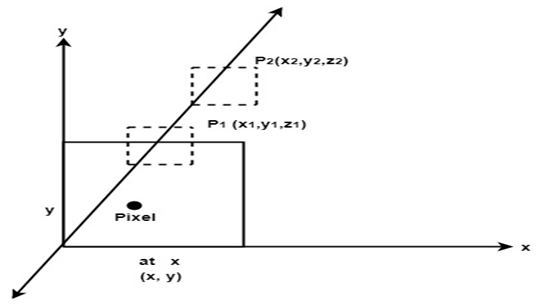
The depth of object is computed by each pixel of the object displayed on the screen from this we get to know about how object closer to the observer.
The record of intensity is also keep with the depth that should be displayed to show the object.
It is an extension of frame buffer.
Two arrays are used for intensity and the depth, the array is indexed by pixel coordinates (x,y).
Algorithm:
Initially set depth(x,y) as (1,0) and intensity (x,y) to background value.
Find all the pixels (x,y) that lies on the boundaries of polygon when projected onto the screen.
To calculate pixel coordinates:
Calculate the depth z of the polygon at (x,y).
If z < depth (x,y) then this polygon lies closer to the observer else others are already recorded for this pixel.
Set depth (x,y) to z and intensity(x,y) to the value according to polygon shading.
If z > depth (x,y) then this polygon is new and no action taken.
After all polygons have been processed the intensity array will contain the solution.
This algorithm contains common features to the hidden surface algorithm.
It requires the representation of all opaque surface in scene polygon in the given figure below.
These polygons may be faces of polyhedral recorded in the model of scene.
It is also called as painter algorithm because of paininting of frame buffer is done in decreasing order of distance.
This algorithm comes under the category of list priority algorithm.
The ordering of visibility of an object is done in this algorithm.
The result will be correct if the object are reversed in particular order.
The objects are ordered in increasing manner to z coordinate.
The rendering of object done in order of z coordinate.
Next the object will be obscure near one.
The pixel of near one get overlapped on the further objects.
If z values of two overlap then the result will determine correctly as shown in figure.
If z value overlap each other then the correct answer can be maintained by splitting of object.
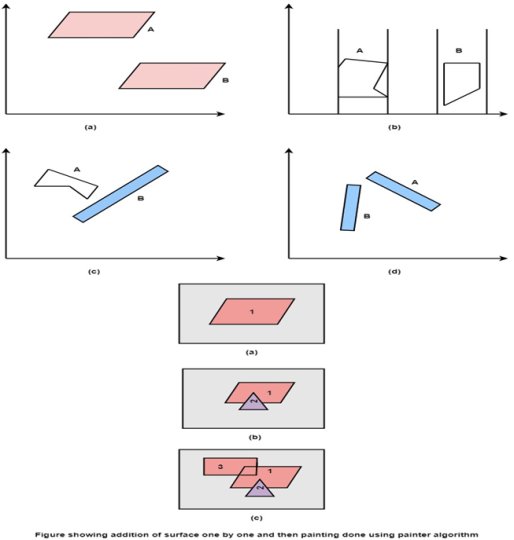
The painter algorithm finds the distance from view plane and then polygons with more distance are painted first.
Painter algorithm:
Start
Sort all polygon with z value keep the largest value first.
Scan converts polygon in this order. Following test is applied:
Does A is behind and non-overlapping B in the dimension of Z.
Does A is behind B in z and no overlapping in x or y.
If A is behind B in Z and totally outside B with respect to view plane.
If A is behind B in Z and B is totally inside A with respect to view plane
The success of any test with single overlapping polygon allows F to be painted.
Following figure shows the test applied on the objects.
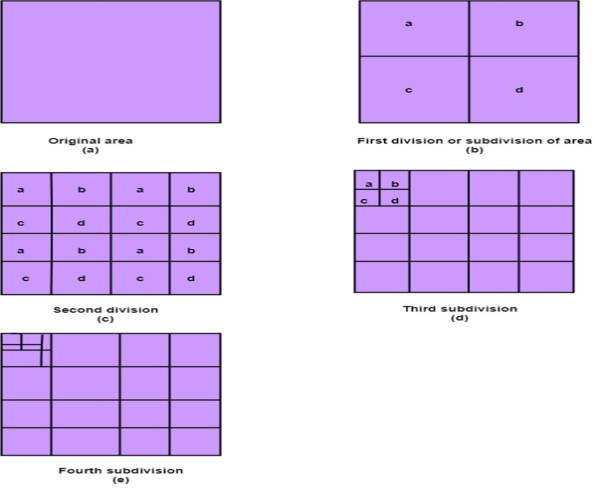
It is developed by John Warnock hence it is referred as Warnock algorithm.
In this the working of divide and conquer is applied.
The fundamental area of coherence is used.
The visibility of algorithm can be resolved by this algorithm.
The classification of polygon takes place as trival polygon and non-trival polygon.
The trival polygons are easy to handle.
The non-trival polygons are divided into 4 equal sub windows then further division takes place until it becomes the trival polygon.
Following figure shows the classification of polygon takes place as trival polygon and non-trival polygon.
Following are four categories of polygons in Warnock algorithm:
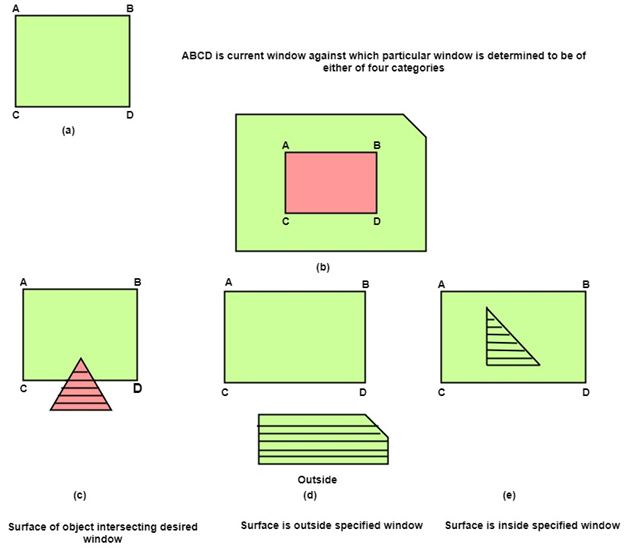
Inside Surface: The surface that comes completely inside the boundaries or surrounding window.
Outside Surface:The surface that comes completely outside the boundaries or surrounding window.
Overlapping Surface:The surface that completely encloses the polygon surface or the surface that partially inside or outside the surface area.
Following figure shows the four categories of polygons in Warnock algorithm: