UNIT-2
POLYGON, WINDOWING AND CLIPPING
Polygon is an ordered list of vertices.
The plane that is described as the number of straight line segments connected to form a closed polygonal chain.
The polygon chain is connected by edges and the points that are connected by edges are vertices of polygon.
The interior of the solid polygon is called as body.
The simple polygon is the polygon which does not intersect itself.
Following figure shows the polygon:

There are three types of polygon according to their convexity or type of non-convexity as:
Convex Polygon:
It is a simple polygon which does not intersect itself.
In convex polygon the points are connected at the boundary only.
The line segments are not going outside the polygon.
It has a simple interior as convex set.
All interiors in the convex polygon are less than or equal to 180 degree.
In strict convex polygons the angles are compulsory less than the 180 degree.
In this polygon the points are inside or on the boundary of the polygon.
The edges define the closed half-plane as polygon.
For each edge the interior point are all on the same side of the line that the edge defines.
The edges are of convex hull.

Concave Polygon:
The concave polygon is the polygon which has one or more angles that are greater than 180 degree.
It should have at least four sides.
It has irregular shapes.
It is not convex polygon.
It is opposite of convex polygon.
The polygon is said to be concave polygon when one of the interior angle is greater than 180 degree.
The area and the parameter are depend on the shape of the polygon.
The vertices of concave polygon are inward and outward.
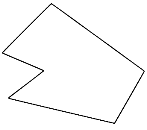
Complex Polygon:
A complex polygon has a discrete circuit.
The complex polygon can be self-intersecting polygon.
The vertices inside the complex polygons are counted when two edges are connected.
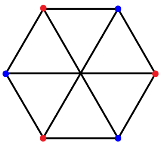
It is also known as the counting number method.
While filling the object we often need to identify whether particular point is inside or outside an object.
Following are two methods that are used to find whether point is inside or outside an object.
Polygon is an ordered list of vertices that are connected by edges.
For filling the polygon we need to check pixel falling on the boundary of the polygon or inside-outside of the polygon.
Following are the polygon filling algorithms:
2.4.1 Flood Fill Algorithm
In boundary fill algorithm the area and the boundary is filled with different colors.
In objects, the boundary is filled with color by searching for a particular boundary interior color.
Instead the searching for particular boundary we can paint object by specified interior color.
It relies on the fill color instead of relying on the boundary of object.
It replaces the interior color with the fill color in the object.
This process continues till all the pixels paint by the fill color, when no more pixel of the original interior color exist the algorithm completed.
The algorithm relies on the 4 connected and the 8 connected method of filling in the pixels.
This process looking for all adjacent pixels that are a part of the interior.
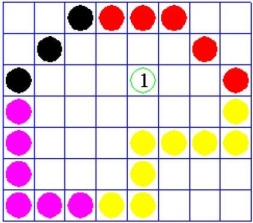
2.4.2 Scan Line Fill
Scan line is the line which intersects the polygon.
This algorithm works by intersecting scan line with polygon edges.
This fills the polygon between the pairs of intersection.
Following are some steps to perform scan line algorithm:
Step 1: find out the Ymin and Ymax from given polygon.
Step 2: the scan line should be intersects all the edges between Ymin to Ymax. Name the intersection points of the polygon.
Step 3: sort the points of intersection according to X coordinate.
Step 4: the points that are inside the polygon fill it and ignore other points.
Following figure shows the scan line algorithm:
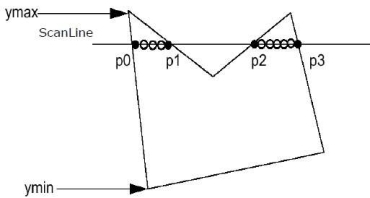
2.4.3 Seed Fill
The seed fill algorithm is works with picking a point inside an object.
The process starts with filling the pixels until it hits the boundary,
As it gets the color of boundary different than the fill color, the algorithm completed.
This algorithm is also known as boundary fill and flood fill algorithm.
The algorithm works on 4 connected or 8 connected pixels.
In this algorithm, the color of boundary is assume same for entire object.
Following figure shows the 4 connected and 8 connected boundary fill algorithm.
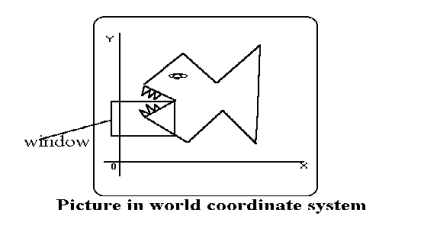
Windowing:
The portion of screen where the selection and enlarging the portion of drawing method is used is called as windowing.
The world coordinates are used to select window.
The window becomes an imaginary box where we select objects or enclose the area of the object.
The size of window is (0,0) coordinates which is bottom left corner and towards the right side until the window encloses the desired area.
The area on display device where the window is mapped is called as viewport.
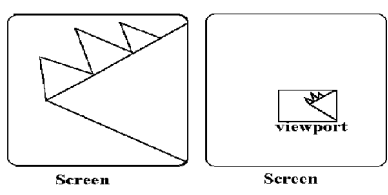
Clipping:
The viewport is a section of screen where the images are encloses by the window on the world coordinate system will be drawn.
When a window is placed on the object and parts of the objects can be seen.
The points and the lines that are outside the window are cut off from view.
This process of cutting off parts of the image on the screen is called as clipping.
In clipping we examine the object with each line that comes completely inside the window, completely outside the window or crosses the window.
If the lines are inside the window then lines will be displayed, if the lines or points are completely outside the window then it is not displayed.
If the line and the points are crosses the window then the part of intersection will be taken and the portion which comes inside the window that will be displayed other part will be not displayed.
Below figure shows the clipping process.
The viewing transformation is the mapping part of the world coordinate scene to device coordinate.
The viewing transformation is also called as the window to viewport transformation or windowing transformation.
Following figure shows the viewing transformation using standard rectangle for window and viewport.
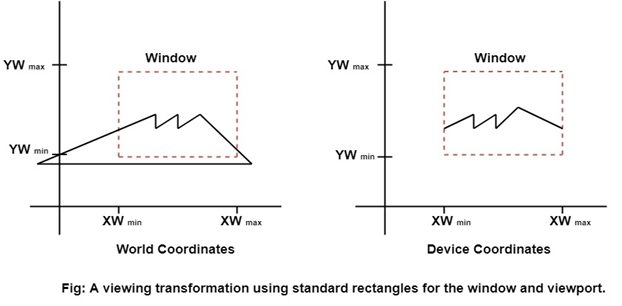
Following are some steps to perform viewing transformation:
The line clipping is same as the point clipping method.
The line that is outside the window is cut and the line which is inside the window that will be displayed.
This algorithm uses the line clipping method.
The minimum coordinates for the clipping region is (XWmin, YWmin) and the maximum coordinates are (XWmax, YWmax).
As below figure shows the concept of cohen Sutherland line clipping.
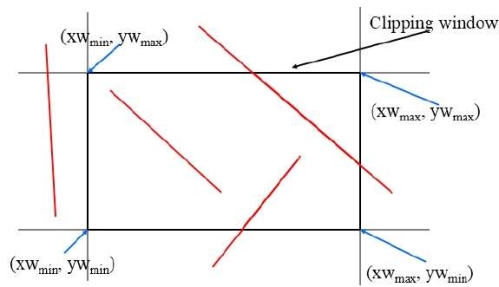
There are three possibilities for line as-
The 4bits are used to divide the entire region.
This 4 bits represents the top, bottom, top and left as the figure shows.
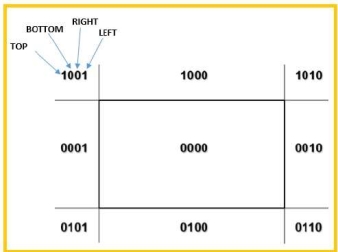
Following are steps to perform the cohen Sutherland algorithm which are based on 4 bits that are given above.
- Choose an end points of the line that is outside the window.
- Find the intersection point at the window boundary.
- Replace the endpoints with that intersection points and update the region code.
- Repeat step 2 until we get the clipped line either trivially accepted or trivially rejected.
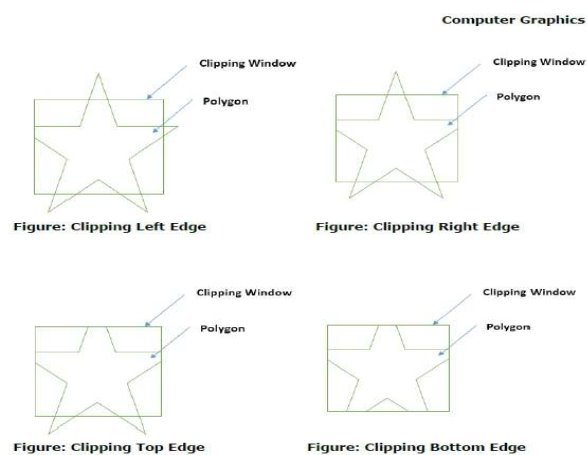
The Sutherland hodgeman polygon clipping algorithm is used for polygon clipping.
The polygon can also be clipped by specifying the clipping window.
All the vertices of the polygon are clipped against each edge of the clipping window.
First the polygon is clipped against the left edge of the polygon window to get new vertices of the polygon.
The new vertices are used to clip the polygon against right, top and bottom edge.
While processing an edge of a polygon with clipping window, an intersection point is found if edge is not completely inside the clipping window and the partial edge from the intersection point to the outside edge is clipped.
It is a polygon clipping method where this algorithm also can clip the concave polygons like Sutherland Hodgeman algorithm.
This algorithm used in various areas like computer graphics, game development and other where clipping of polygon is needed.
It allows the arbitrarily shaped clipping polygon or area to be clipped.
This algorithm applies generally in 2D.
This algorithm does not work for itself intersecting polygons.
Steps to be performed to solve the Weiler Atherton polygon clipping algorithm:
Example:
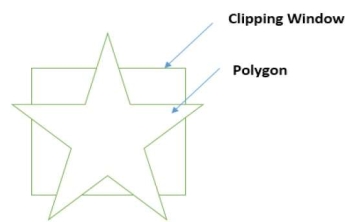
The given figure shows the polygon which is going to be clipped.
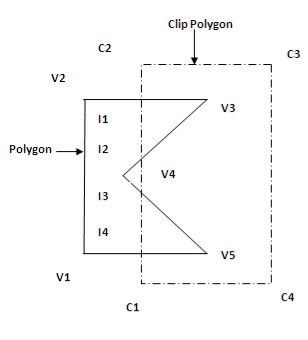
Here, vertices of the subject polygon are V1, V2, V3, V4 and V5.
C1, C2, C3 and C4 are the clipping polygon region and I1, I2, I3 and I4 becomes the intersection points.
In this example we will start traversing from the intersection point I1 while going clockwise we got the sequence as I1, V3, I2.
Here, the leaving intersection occurred hence we go for clip polygon vertex list.
As per the list of intersection points and the vertices of the subject polygon we will traverse it from the downward direction of the polygon.
The process will start again by traversing the intersection point I3.
Then the second traversal starts from I3, V5, and I4.
Again the leaving intersection points happed again check for the list.
Here no other vertex is left hence we will stop the algorithm.
Therefore, first traversal gives the polygon as: I1, V3, I2, I1 and second traversal gives the polygon as: I3, V5, I4, I3.