Unit - 4
Impact of Free Jets
Momentum is defined as the product of mass, m and the velocity, V of the body.
Momentum = m.V
According to second Newton's law of motion, the magnitude of the applied force is equal to rate of change of momentum.
Force is a vector quantity which has both the magnitude and direction. Therefore, the direction of force will depend on the direction in which the change of momentum take place.
Therefore,
Applied force, F
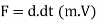
On differentiating the Equation we have,
In applied mechanics we deal with solid bodies where the mass of body remains constant. i.e., dm/dt = 0
Equation (1) as applied in mechanics reduces to
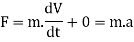
Therefore dm/dt = 0 thus the equation we get,
Where V2 and V1 are the velocity of fluid at section 1 of fluid stream resp
Mass flow rate of fluid m = 
Where 
= is density of fluid and Q is volume flow rate.
Therefore, equation is reduced to:
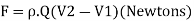
Equation represents the force F exerted by the body on fluid. Using the third Newton’s law of motion the force excreted by the fluid on body will equal and opposite. It implies that,
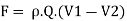
Key takeaways:
- Momentum is defined as the product of mass, m and the velocity, V of the body.
Momentum = m.V
2. According to second Newton's law of motion, the magnitude of the applied force is equal to rate of change of momentum.
3. Force is a vector quantity which has both the magnitude and direction.
Consider a jet of water of cross-sectional area A moving with a velocity V which impinges on a fixed plate.
Jet may impinge (strike) in direction or on an inclined plate.
Then volume flow rate of fluid, Q = A.V
Mass flow rate, in
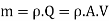
Jet may strike the fixed plate either in normal direction or at some angle. It is assumed that the plate is perfectly smooth Le friction between the jet and the plate is neglected, there is no lo energy during impact of jet and the velocity of jet is uniform throughout.
When the Fixed Plate is Normal to Jet
Derive an expression for the force exerted by the jet of water on a stationary flat plate held normal to the plate.
Consider a fluid jet striking a fixed plate normal to jet shown in Fig.
A = cross-sectional area of jet,
V= velocity of jet, m/s
P= density of fluid, kg/m
Since plate is fixed its velocity is zero
When the jet strikes the plate, its momentum is completely destroyed by the application of force and its final velocity becomes zero. Therefore, force acting on the plate in the direction normal to plate can be determined by using impulse momentum Equation
Force
m =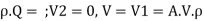 
Since the plate is stationary, therefore, work done on plate is zero
When fixed plate is inclined at an angle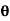 
With jet
Consider the fixed plate inclined at an angle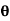 
as shown in Fig.
Vis the velocity of jet in the X-X direction
Resolution of velocity normal and parallel to the plate is shown in Fig.
Velocity of jet normal to plate = Vsin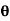 
- Normal force on plate
Using impulse momentum Equation, normal force to jet we get.
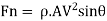
2. Force on plate in X-X and Y-Y direction
By resolving the normal force in (X-X) and (Y-Y) directions as shown in Fig
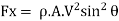
In this case also, the work done on the plate is zero since the plate is stationary
3. Ratio of discharges tangential to plate
Let Q, and Q, be volume flow rate along the plate out of the stream of jet at the rate of Q striking on the plate as shown in Fig.
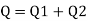
Since the resultant force in tangential direction on plate is zero. Applying impulse- momentum equation in tangential direction to plate, we get.
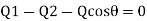
On solving equation we get,
Key takeaways:
- When the jet strikes the plate, its momentum is completely destroyed by the application of force and its final velocity becomes zero.
- Therefore, force acting on the plate in the direction normal to plate can be determined by using impulse momentum Equation
Consider a vertical flat plate of height h (m) hinged at the top edge O as shown in Fig. Plate When the plate is vertical a jet of area A at a velocity V strike the in normal direction at a distance 'y' (m) from top edge.
Due to the normal force, F, exerted by the jet on the plate, it will tend to swing about 'O'. Order to keep the plate in vertical position, a force P is applied at the bottom edge of the plate in the direction opposite to the fluid jet force.
For equilibrium of the plate, the moment of the forces about the hinge must be zero. Therefore,
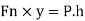
But the force exerted by jet,
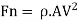
On substituting the value of F, from Equation (ii) in (i), we get.
Holding force, P
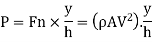
Angle Turned by Plate when Holding Force P is not applied
In case the holding force P in the horizontal direction is not applied, the hinged plate will swing about O.
Let the angle turned by the plate by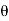 
The plate is under the equilibrium due to moment caused by the force of jet and the moment caused by the weight of plate, W.
Plate OGCA is moved to OG1, C1, A1.
Component of fluid force F in normal direction,
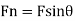
For equilibrium,
Moment of force Fn, about hinge = Moment of weight about hinge
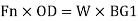
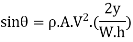
Key takeaways:
- Consider a vertical flat plate of height h (m) hinged at the top edge O as shown in Fig. Plate When the plate is vertical a jet of area A at a velocity V strike the in normal direction at a distance 'y' (m) from top edge.
- Due to the normal force, F, exerted by the jet on the plate, it will tend to swing about 'O'. Order to keep the plate in vertical position, a force P is applied at the bottom edge of the plate in the direction opposite to the fluid jet force.
Consider a fluid jet of cross-sectional area & a velocity a smooth stationary carved plate at its centre as shown in Fig.
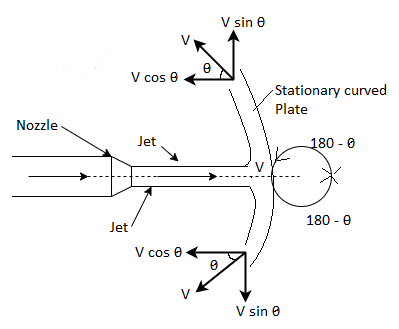
The jet comes out at the same velocity V along the curved surface
Components of velocity in (X-X) and (Y-Y) directions are V Cos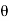
and V sin respectively.
Mass flow rate,
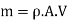
Initial velocity of jet in (X-X) direction, V1= V
Final velocity of jet in (X-X) direction, V₂ = -Vcos
According to impulse momentum Equation
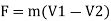
Force in (X-X) direction
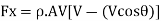
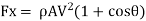
Similarly, force in (y-y) direction will be
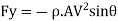
Negative sign indicates that the force Fy acts in downward direction
Unsymmetrical Curved Plate at One End Tangentially
Consider a jet of velocity V striking tangentially to an unsymmetrical curved plate as shown in Fig.
Let the plate tip angles be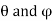 
Initial velocity components at inlet are:
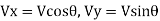
Final velocity components at exit are
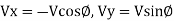
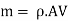
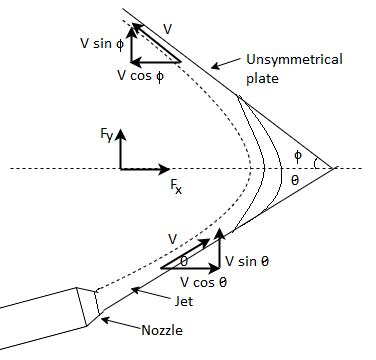
Using impulse momentum equation, the force exerted on plate in (X-X) and (Y-Y) directions will be:
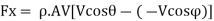
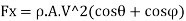
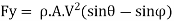
For Semicircular Curved Vane or Plate
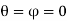the Equations can be modified and the force in normal direction becomes,
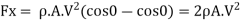
It can be seen that this force exerted on semicircular fixed plate is twice to that of fixed vertical plate is given by equation
Key takeaways:
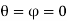the Equations can be modified and the force in normal direction becomes,
It can be seen that this force exerted on semicircular fixed plate is twice to that of fixed vertical plate is given by equation
Consider a jet of water of area A at velocity V strikes a single symmetrical moving curved vane at velocity u as shown in Fig.
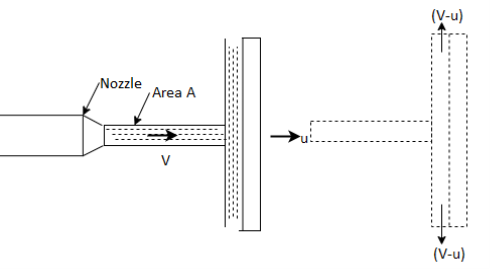
Jet leaves the vane in tangential direction at angle 8 from horizontal at relative velocity (V-u).
Mass flow rate of jet of water striking the vane, m=p. A(V-u) Component of velocity in direction of jet after striking the vane is [-(V-u) cos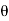
] as shown in Fig.
:. Normal force on vane,
F = m [Initial velocity - Final velocity]
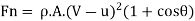
Rate of work done, W = Force x distance travelled/second by vane
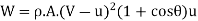
K.E. Supplied to jet
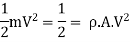
Efficiency of system, η
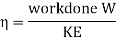
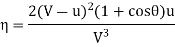
Condition for maximum efficiency d η/du = 0
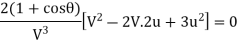
But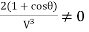 
it follows that:
V= u is not possible since jet will never strike the vane.
Hence the system has the maximum efficiency when
V= 3u
On substituting the above value in equation
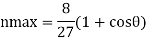
For semicircular vane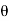 
=0, on substituting the vane of 
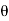in equation we have,
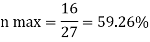
Key takeaways:
Jet leaves the vane in tangential direction at angle 8 from horizontal at relative velocity (V-u).
Mass flow rate of jet of water striking the vane, m=p. A(V-u) Component of velocity in direction of jet after striking the vane is [-(V-u) cos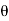
]
The case of single moving vane system is not of any practical use since there is a continually lengthening of jet i.e., the distance between the jet and vane increases by 'u' m/s.
In order that the system could be used to produce the work continuously, a series of curved vanes can be mounted at equidistance around the periphery of a wheel as shown in Fig.
Since series of vanes are available to intercept the jet. Therefore, Mass flow rate striking the vanes S,
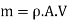
Normal force exerted on vanes,
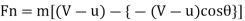
Rate of work done,
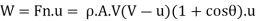
Efficiency of system,
Condition for maximum efficiency is d
/du= 0
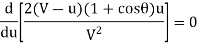
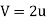
Using the equation, the maximum efficiency becomes
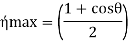
This efficiency is twice that of flat vane given by equation
For semicircular vanes
In the case deflection of jet becomes 180 degree
Key takeaways:
The case of single moving vane system is not of any practical use since there is a continually lengthening of jet i.e. the distance between the jet and vane increases by 'u' m/s.
In order that the system could be used to produce the work continuously, a series of curved vanes can be mounted at equidistance around the periphery of a wheel
Case I: In case of single vane
Consider a jet of water leaving the nozzle at absolute velocity V, and the vane moves with a velocity u shown
The jet will enter at relative velocity. Tangentially at inlet angle of vane 
V₁-V-u.
Let, V₁ = absolute velocity of jet:
u = vane velocity at inlet of vane
α= exit angle of nozzle
inlet angle of moving vane
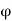= exit angle of moving vane
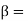angle at which the jet leaves the vane
All angles are measured with direction of motion of vane.
Vw and Vr are the components of absolute velocity in the direction of motion of vane and normal to it resp. Vw is called velocity of whirl or tangential velocity and Vr is called velocity of flow Therefore,
Vw1 = Velocity of whirl at inlet,
Vw2= Velocity of whirl at outlet
Vf₁ Velocity of flow at inlet.
Vf2= velocity of flow at outlet
Inlet velocity diagram
Draw AB to represent the vane velocity u in magnitude and direction. Draw AC to represent jet velocity V, at an angle a in magnitude and direction.
Then vector BC = V, which is equal to (V₁-) represents the relative velocity at inlet which strikes the vague tangentially at an angle 0.
Impact of Jet
The components of V, which represent whirl velocity and velocity of flow at inlet. Whirl component of velocity. V. Is responsible to produce the driving force while the flow component of velocity, V, is possible for flow of water.
Outlet diagram
The water will pass over the vane and leave tangentially with relative velocity Va at an outlet angle of vane o. The absolute velocity of jet V, at outlet can be determined by vector sum of Va and u. It leaves the vane at angle Vand V are components of absolute velocity V, is the direction of motion of vane and normal to it respectively.
If friction between water and vane is neglected then: Relative velocity at outlet V₁ = Relative velocity at inlet, V
Mass flow rate of water striking the vane,
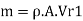
Force exerted in direction of motion of vane, Fx,
Force F, is produced due to change in whirl velocity. Therefore,
Normal force, F. = F₁ = m (Vw1-Vw₂)
But is negative to V, when ß <90. Therefore, magnitude of force,
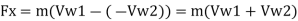
Equation above is applicable only when,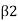 
<90 as shown in Fig.
When,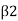 
, 90°. Vw2=0
When,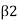 
> 90° 1.c. B, is an obtuse angle. Then V will be positive and in the same direction as V Equation
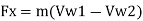
In general,
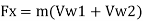
Work done (W)
Work done per second is given as,
W = Force x distance moved by vane in the direction of force per second
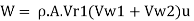
Work done per unit weight of fluid, W,
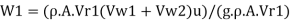
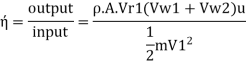
Efficiency of jet, n
Initial kinetic energy of jet
W= Force x distance moved by vane in the direction of force per second
Where, m = Rate of mass flow of water per second in the jet =p AV₁
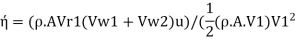
Case II: In case of series of curved vanes
Mass flow rate striking the vanes Mass flow rate issued by jet= p A V₁. Equation for work and Equation
Rate of work done, W
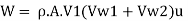
Key takeaways:
The components of V, which represent whirl velocity and velocity of flow at inlet. Whirl component of velocity. V. Is responsible to produce the driving force while the flow component of velocity, V, is possible for flow of water.
For a radial curved vane, the radius of vane at inlet and outlet is different; hence, the blade velocity u will be different at inlet and outlet.
Consider a series of radial vanes mounted on a wheel as shown in Fig.
Let:
N= Speed of wheel be N r.p.m.
R₁ Radius of wheel at inlet N rpm
R₂ Radius of wheel at outlet
Angular speed of wheel,
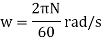
Blade velocity at inlet,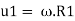 
Blade velocity at outlet,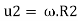
Water may flow racially on vanes either inwards or outwards depending upon whether the water enters the outer or inner periphery of wheel. Velocity diagram at inlet and outlet of vane can be drawn as explained in section above and it is shown in
Mass of water striking the series of vanes per second,
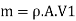
Rate of momentum of water striking the vanes in tangential direction at inlet = m V., (where, V=V, cos a) ... Rate of angular moment of jet at inlet,
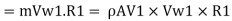
Similarly, Rate of angular moment of jet at outlet,
Torque exerted on wheel, T = The rate of change of angular momentum is defined as torque. Therefore,
Torque, T= Rate of angular momentum at inlet-Rate of angular momentum at outlet
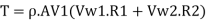
(a) Rate of work done, W
Rate of work done, W
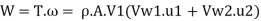
(b) Efficiency of radial curve v e vanes,
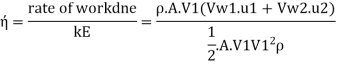
(c) Blade velocity coefficient or friction factor K
When the water over the radial vanes the relative velocity at outlet Vr2 is less than the relative velocity of jet Vr1 due to energy lost in overcoming the friction.
Blade velocity coefficient or friction factor K When water flows over the radial vanes the relative velocity at outlet, V
If friction is neglected K = 1, then Vr2 = Vr₁
(d) Axial thrust on wheel,
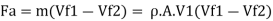
(e) Efficiency of radial vanes when friction is neglected
If friction is neglected, there will not be any loss of kinetic energy of fluid. In this case the, rate of work done will also be equal to decrease in K.E. Of fluid.
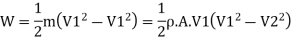
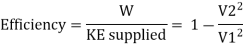
From Equation it is clear that the efficiency would be maximum when V2, is minimum. However, V2, cannot be made zero since the fluid entering the vane will not flow out.
Key takeaways:
- For a radial curved vane, the radius of vane at inlet and outlet is different; hence, the blade velocity u will be different at inlet and outlet.
Case Study:
- Impact of free jet
Case I: In case of single vane
Consider a jet of water leaving the nozzle at absolute velocity V, and the vane moves with a velocity u shown
The jet will enter at relative velocity. Tangentially at inlet angle of vane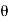 
V₁-V-u.
Let, V₁ = absolute velocity of jet:
u = vane velocity at inlet of vane
α= exit angle of nozzle
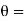inlet angle of moving vane
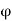= exit angle of moving vane
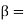angle at which the jet leaves the vane
All angles are measured with direction of motion of vane.
Vw and Vr are the components of absolute velocity in the direction of motion of vane and normal to it resp. Vw is called velocity of whirl or tangential velocity and Vr is called velocity of flow Therefore,
Vw1 = Velocity of whirl at inlet,
Vw2= Velocity of whirl at oulet
Vf₁ Velocity of flow at inlet.
Vf2= velocity of flow at outlet
Inlet velocity diagram
Draw AB to represent the vane velocity u in magnitude and direction. Draw AC to represent jet velocity V, at an angle a in magnitude and direction.
Then vector BC = V, which is equal to (V₁-) represents the relative velocity at inlet which strikes the vague tangentially at an angle 0.
Impact of Jet
The components of V, which represent whirl velocity and velocity of flow at inlet. Whirl component of velocity. V. Is responsible to produce the driving force while the flow component of velocity, V, is possible for flow of water.
Outlet diagram
The water will pass over the vane and leave tangentially with relative velocity Va at an outlet angle of vane o. The absolute velocity of jet V, at outlet can be determined by vector sum of Va and u. It leaves the vane at angle Vand V are components of absolute velocity V, is the direction of motion of vane and normal to it respectively.
If friction between water and vane is neglected then: Relative velocity at outlet V₁ = Relative velocity at inlet, V
Mass flow rate of water striking the vane,
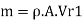
Force exerted in direction of motion of vane, Fx,
Force F, is produced due to change in whirl velocity. Therefore,
Normal force, F. = F₁ = m (Vw1-Vw₂)
But is negative to V, when ß <90. Therefore, magnitude of force,
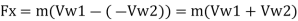
Equation above is applicable only when,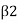 
<90 as shown in Fig.
When,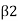 
, 90°. Vw2=0
When,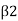 
> 90° 1.c. B, is an obtuse angle. Then V will be positive and in the same direction as V Equation
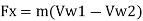
In general,
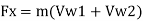
Work done (W)
Work done per second is given as,
W = Force x distance moved by vane in the direction of force per second
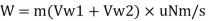
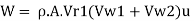
2. Torque exerted on a wheel with radial curved vanes.
For a radial curved vane, the radius of vane at inlet and outlet is different; hence, the blade velocity u will be different at inlet and outlet.
Consider a series of radial vanes mounted on a wheel as shown in Fig.
Let:
N= Speed of wheel be N r.p.m.
R₁ Radius of wheel at inlet N rpm
R₂ Radius of wheel at outlet
Angular speed of wheel,
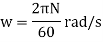
Blade velocity at inlet,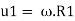 
Blade velocity at outlet,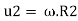
Water may flow racially on vanes either inwards or outwards depending upon whether the water enters the outer or inner periphery of wheel. Velocity diagram at inlet and outlet of vane can be drawn as explained in section above and it is shown in
Mass of water striking the series of vanes per second,
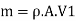
Rate of momentum of water striking the vanes in tangential direction at inlet = m V., (where, V=V, cos a) ... Rate of angular moment of jet at inlet,
Similarly, Rate of angular moment of jet at outlet,
Torque exerted on wheel, T = The rate of change of angular momentum is defined as torque. Therefore,
Torque, T= Rate of angular momentum at inlet-Rate of angular momentum at outlet
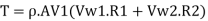
(a) Rate of work done, W
Rate of work done, W
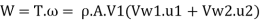
(b) Efficiency of radial curve v e vanes,
(c) Blade velocity coefficient or friction factor K
When the water over the radial vanes the relative velocity at outlet Vr2 is less than the relative velocity of jet Vr1 due to energy lost in overcoming the friction.
Blade velocity coefficient or friction factor K When water flows over the radial vanes the relative velocity at outlet, V
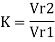
If friction is neglected K = 1, then Vr2 = Vr₁
(d) Axial thrust on wheel,
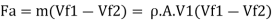
(e) Efficiency of radial vanes when friction is neglected
If friction is neglected, there will not be any loss of kinetic energy of fluid. In this case the, rate of work done will also be equal to decrease in K.E. Of fluid.
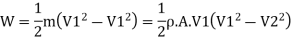
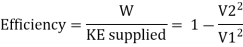
From Equation it is clear that the efficiency would be maximum when V2, is minimum. However, V2, cannot be made zero since the fluid entering the vane will not flow out.
References:
- Engineering Fluid Mechanics, Garde and Mirajgaonkar, Scitech
- A Text Book on Fluid Mechanics and Hydraulic Machines, Sukumar Pati, McGraw Hill,
New Delhi
3. A Text Book of Fluid Mechanics and Hydraulic Machines, R K Bansal, Laxmi
Publications Pvt. Ltd., New Delhi
4. Fluid Mechanics, Fundamentals and Applications, Yunus A Cengel and John Cimbala, McGraw Hill International, New Delhi
5. Fluid Mechanics by Frank M White, McGraw Hill
6. Fluid Mechanics by Streeter, Wylie and Bedford, McGraw Hill International, New Delhi
