Unit - 5
Earth Pressure
Lateral earth pressure
Active earth pressure
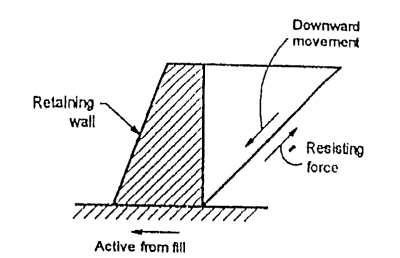
Fig.5.1: Active earth pressure
Passive earth pressure

Fig.5.2: Passive earth pressure
Back fill:
Surcharge
Assumptions made by Rankine for Earth Pressure:
Assumptions of the Rankine theory for active earth pressure are as follows:
Key Takeaways:
There are different types of earth pressures in the lateral direction according to the structure against which the soil is retained and according to the equilibrium conditions. These are: Earth pressure at rest, active earth pressure, passive earth pressure.
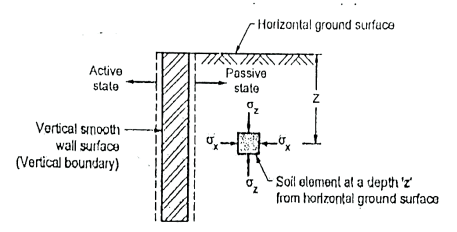
Fig.5.3: A semi-infinite mass of soil bound by a horizontal surface and a vertical boundary
Key Takeaways:
Rankine's was the only engineer who developed the concepts of plastic equilibrium to solve the stability problems. When plastic equilibrium conditions are realised in limited zones of soil, then it is termed as the local state of plastic equilibrium
When Wall Moves Away from Backfill:
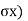
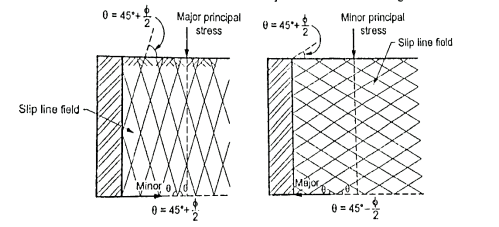
Fig.5.4: Active and passive Rankine state due to wall movement
Active Rankine state
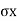
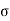
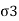
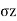
When Wall Move towards the Backfill
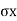
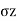
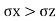
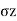
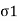
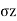
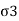
Passive Rankine state


Key Takeaways:
There are two situations:
P0=K0 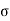 z
z
Where K0=Coefficient of earth pressure
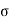 z=Effective vertical stress at depth a
z=Effective vertical stress at depth a

Fig.5.5: earth pressure at rest
Key Takeaways:
Earth pressure at rest exerted on the back of a rigid retaining wall can be determined by using the theory of elasticity in which soil is assumed to be elastic, homogeneous, isotropic and semi-infinite.
These two components are as follows,

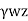
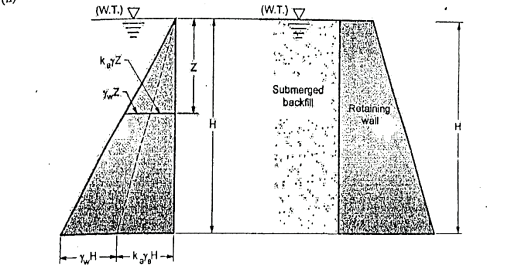
Fig.5.6: Submerged backfill
Here at any depth 2 below the horizontal surface-active pressure is given by the following expression,
Pa=Ka sz+
sz+ z
z
where, Pa=active pressure
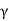 s= submerged weight of soil (y)
s= submerged weight of soil (y)
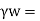 unit weight of water
unit weight of water
Fig. shows the active earth pressure distribution diagram at any depth 'z' and at the depth H.
The active pressure at the base of wall, where z H is given by the following expression,
Pa=Ka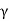 sH+
sH+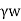 H
H
Key Takeaways:
The active pressure at the base of wall, where z H is given by the following expression, Pa=KaγsH+γwH
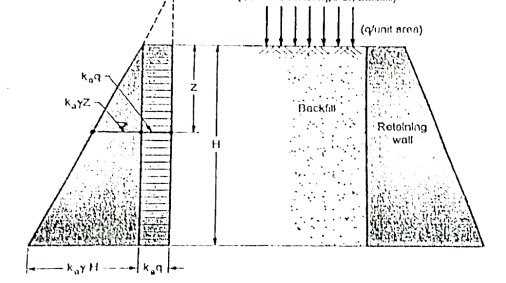
Fig.5.7: Retaining wall with backfill carrying uniform surcharge
∴Lateral active pressure at any depth 'z' is given by the following expression
Pa=Ka z+Kaq …. (At any depth z)
z+Kaq …. (At any depth z)
where z =H, then, active pressure at the base is given
Pa=Ka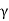 H+Kaq ......(at height H from base of wall)
H+Kaq ......(at height H from base of wall)
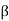
Pa= Ka γz , ...For sloping surface
, ...For sloping surface
Where, Ka=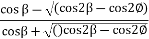
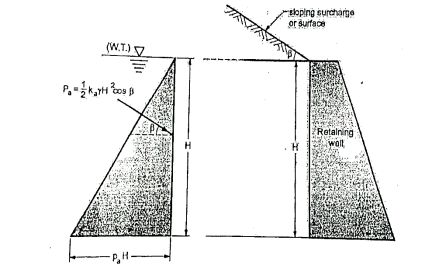
Fig.5.8: backfill with sloping surface
For horizontal ground surface; 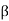 =0
=0
Ka=
The total active pressure P, for a retaining wall having height 'II' is given by the following expression:
Pa=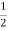 Ka
Ka H2
H2 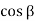
There are two cases for lateral pressure in layered soils which are as follows
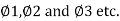
(a) Lateral pressure for layered cohesionless soil
1. Same angle of shearing resistance with cohesionless soil layers
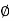
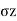
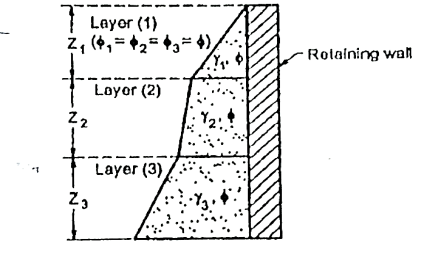
Fig.5.9: Layered soil with same angle of shearing resistance
(2) Different angle of sheering resistance with cohesionless soil layer
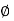
Fig. shows layered soil with different angle of shearing resistance.
Let consider for the two layers as shown in Fig.
for the two layers as shown in Fig.
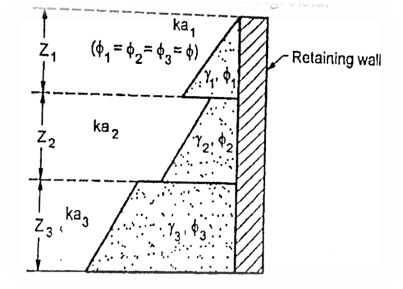
Fig.5.10: Layered soil with different angle of shearing resistance
For these two layers, ka1 > ka2, the active pressure are as follows:
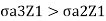
Key Takeaways:
There are two cases for lateral pressure in layered soils which are as follows
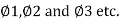
Basic Assumptions of Coulomb's Wedge Theory:
Following are the various basic assumptions of coulomb's wedge theory
Shape of the failure surface:
Active earth pressure (Pa) for C= 0 backfill:
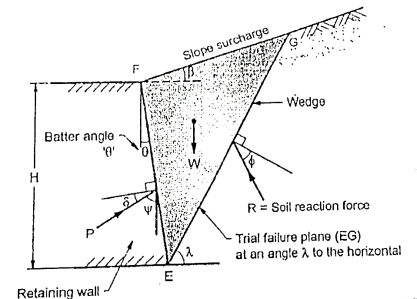
Fig.5.11: Wedge under the action of three forces, W, R and P
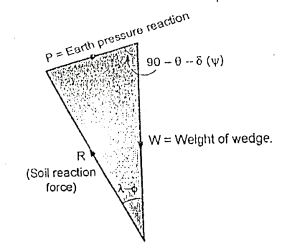
Fig.5.12: Force triangle W, R and P
Active earth pressure for C- 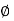 backfill:
backfill:
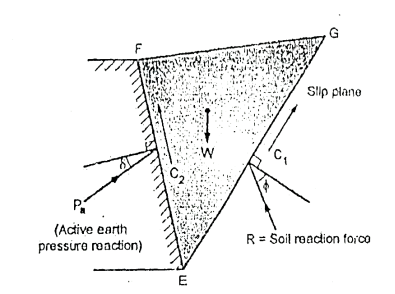
Fig.5.13: Forces acting on soil wedges at failure
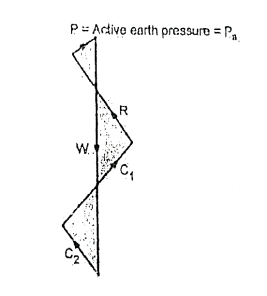
Fig.5.14: Polygon of forces
The force polygon as shown in Fig. is drawn from the known values of W. C, C, and direction of all five forces and the value of p i.e., active earth pressure can be determined by closing side of a polygon.
Here C1=Cu x length of the slip plane EG
C2= unit adhesion (Cw) x length of wall in contact with the soil EF
Key Takeaways:
Rankine's theory of earth pressure considers the theory of plasticity approach to find the stresses in the soil mass. The Rankine's theory is only applicable to smooth vertical wall. There are various ideal conditions used in practice of retaining wall problems. Coulomb's wedge theory can be applied to determine the active earth pressure for a backfill possessing both cohesion and effect of friction between the backfill and wall.
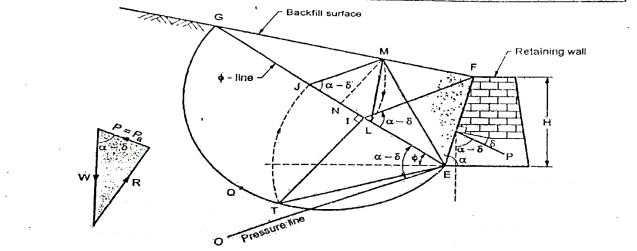
Fig.5.15 Graphical method by poncelet construction based on Rebhann’s principles
Procedure of graphical method:
Following is the procedure of construction to find out the active earth pressure by graphical method refer Fig.
After this construction from step 1 to 10, it shows the  LIM. Area of
LIM. Area of 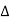 LIM in its natural units multiplied by the unit weight of the soil (
LIM in its natural units multiplied by the unit weight of the soil (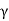 ) gives the active earth pressure (Pa) as follows:
) gives the active earth pressure (Pa) as follows:
Pa=Area of triangle LJM=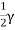 *JM*MN
*JM*MN
Where, 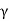 =unit wt of the soil
=unit wt of the soil
JM length of a triangle LJM
MN=height of  LJM
LJM
Pa=Active earth pressure
Key Takeaways:
In 1871, Rebhann's represented a graphical method to determine the total active pressure (Pa) based on Coulomb's theory on a rough wall with a cohesionless, homogenous and inclined backfill.
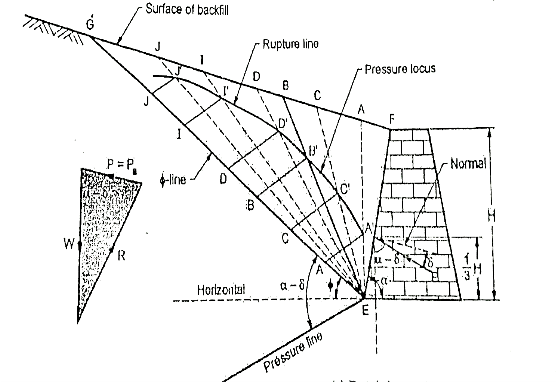
Fig.5.16: Culmann’s graphical method for determining active earth pressure
Graphical construction procedure;
Key Takeaways:
Culmann's graphical method is rather general method than Rebhann's method. This method is same as the trial wedge method.
References: