Unit 5
Open Flow Channel
2. Prismatic and Non-prismatic :
3. Rigid and Mobile Boundary Channels:
Geometric elements of a channel:
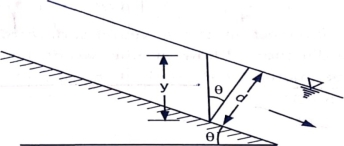
2. Depth of Flow Section 'd': It is the depth of flow normal to the direction of flow
 . Cos
. Cos 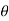 or y =
or y = 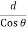
If the slope angle 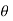 is very small, y
is very small, y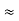 d.
d.
3. Stage: It is the elevation or vertical distance of the free surface above a datum.
4. Top Width 'T': It is the width of the channel section at the free surface.
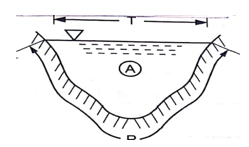
5 Water Area (or area of flow) 'A': it is the cross-sectional area of flow normal to the direction of flow.
6. Wetted Perimeter (p): It is the length of the line of intersection of the wetted surface of the channel with the cross-sectional plane normal to the direction of flow.
7. Hydraulic Radius 'R': It is the ratio of the area of flow (A) to the wetted perimeter (P). R=
8. Hydraulic depth 'D': It is the ratio of the area of flow (A) to the top width (T).
D = 
9. The Section Factor for Critical Flow 'Z': Itis the product of the area of flow (A) and the square root of hydraulic depth (D). = A 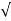 D
D
10.The Section Factor for Uniform Flow Computation: It is the product of the area of flow (A) and the two-thirds power of hydraulic radius (R)
Section factor for uniform flow computations = A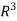
(a) Continuity Equation
(b) Energy Equation
(c) Momentum Equation
(a) Continuity Equation :

Inflow in the element = [Q -  ].
].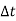 ................1
................1
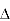
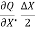
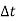
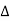
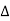
= [Q - 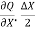 ] .
] .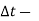 [Q +
[Q +  ].
].
= - 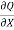 .
. 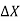 .
.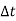 .............3
.............3
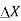
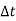
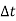
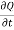
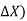
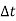
-  .
.  .
.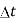 =
= 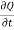 (A.
(A. 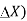 .
.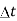
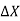
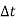
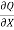
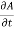
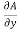
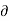
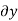
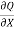 +
+ 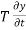 =0 ........6
=0 ........6
Q = AV, where A is the area and V the average velocity
Q = AV in equation 6 , we get
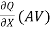 +
+  =0 ..................7
=0 ..................7
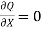 or Q=constant
or Q=constant
Q= A1 V1= A2 V2 =A3 V3 = constant . ..........8
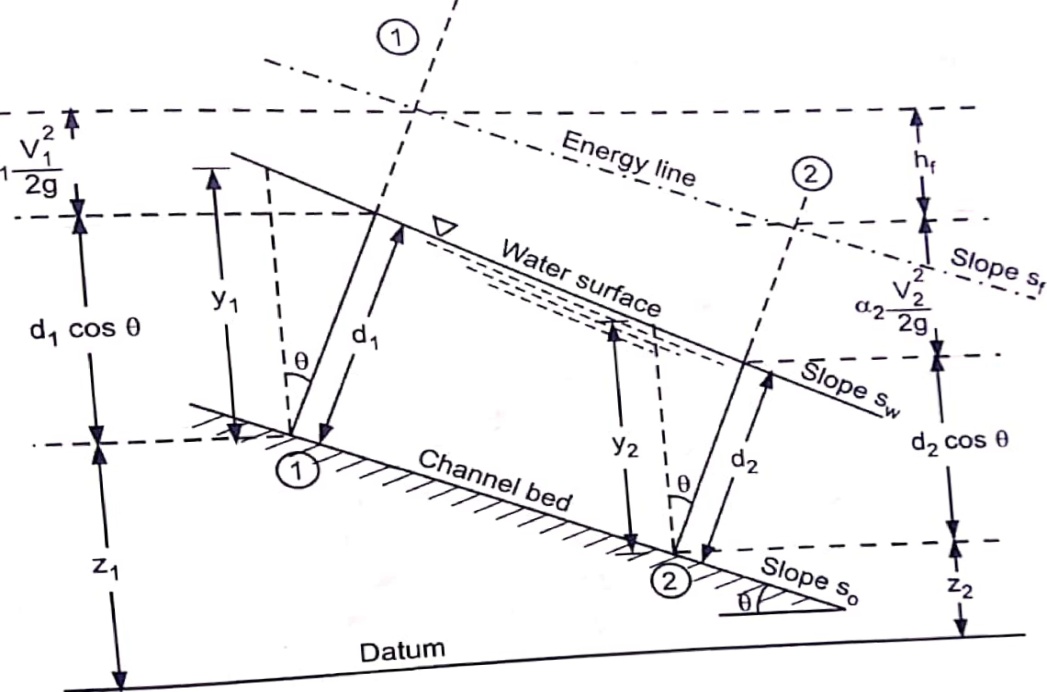
(b) Energy Equation :
Z+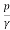 +
+ 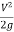 = constant
= constant
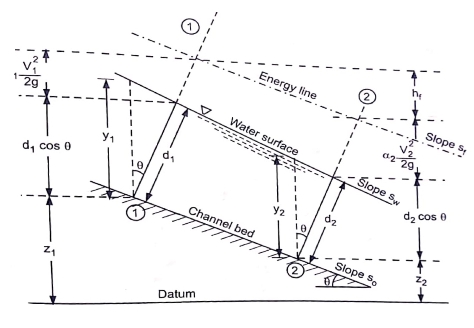
Z1 + d1 cos 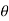 +
+ 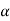 1
1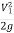 = Z2 + d2 cos
= Z2 + d2 cos 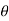 +
+ 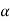 2
2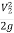 +hf .....................9
+hf .....................9
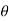
Z1 + y1 + 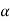 1
1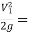 Z2 + y2 +
Z2 + y2 + 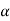 2
2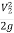 +hf ...........................10
+hf ...........................10
If further, 1 =
1 = 2 = 1
2 = 1
Z1 + y1 + 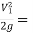 Z2 + y2 +
Z2 + y2 + 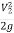 +hf ..........................11
+hf ..........................11
(c) Momentum Equation :
(1) F1 and F2, the hydrostatic forces acting on faces 1-1 and 2-2.
(2) Ff, the frictional force at the boundary of the channel.
(3) Fa, the force due to air resistance at the free surface.
(4) W sin  , the body force i.e. a component of the weight of the liquid in the direction of motion.
, the body force i.e. a component of the weight of the liquid in the direction of motion. is the slope of the bed of the channel.
is the slope of the bed of the channel.
F1 - F2 + W sin  - Ff - Fa =
- Ff - Fa = 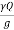 (V2 – V1) .....................12
(V2 – V1) .....................12
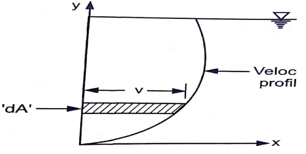
(A) Average Velocity of Flow :
PQ = v dA
Q =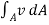
Q = A V
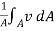
(B) The Discharge :
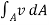
(C) Kinetic Energy :


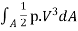
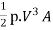
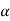

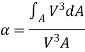
The energy correction factor, 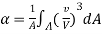 ...................13
...................13
K.E.=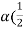 p
p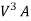 ) .....................14
) .....................14
(d) Momentum :
= (pv dA) .v
=p 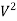 dA
dA
=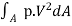
=p  A
A

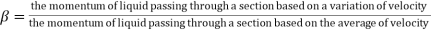

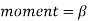 .p A
.p A 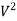
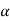

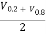
Uniform flow in open channels:
Uniform flow formulae:
Assumptions Made in Chezy's Equation :
1) The flow is steady
2) Channel is prismatic.
3) The bed slope of the channel is small.
Chezy's Formula for Steady Uniform Flow-through Open Channel :
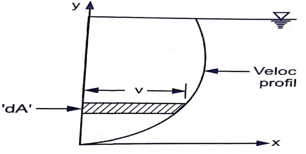
Let, P = Wetted perimeter of cross-section
A = Uniform cross-sectional area
L = Length of the channel
v = Mean velocity of flow
f = Frictional resistance per unit area at unit velocity
Y = Specific weight of water
According to Froude law , the frictional resistance in a length L of the channel
F = f x contact area x ( velocity )2 = f x PL x v2
Work done against the friction per second
Work done = Frictional resistance x distance
= f PLv2 x v = f PLv3
Weight of water between the two section =  AL
AL
This amount of water will fall vertical downward by a distance v in one second
height of fall = v S
Loss of potential energy in one second = Weight x height of fall = ( AL ) v S
We know ,
Work done against friction = Loss in potential energy
f PLv3 = (  AL ) v S
AL ) v S
v3 =  x
x  S
S
v = 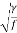 x
x 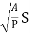
v = C 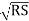
Where C = Chezy's constant = 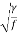
R = hydraulic mean depth = 
Discharge Q = A x v = AC 
1) Surface roughness
2) Vegetation
3) Channel irregularities
4) Channel alignment
5) Silting and scouring.
6) Stage and discharge
7) Transport of suspended and bed material
8) Size and shape
9) Obstruction
1) Surface roughness :
2) Vegetation :
3) Channel irregularities :
4) Channel alignment :
5) Silting and scouring:
6) Stage and discharge:
7) Transport of suspended and bed material :
1) Normal depth :
2) Conveyance :
Q = C A = K
= K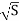 Where K = C A
Where K = C A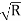
For manning's formula
Q = K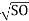 , Where K =
, Where K =  A R2/3
A R2/3
3) Section factor:
Z = A R2/3
4) Hydraulic exponent for uniform flow :
K 2= C yN
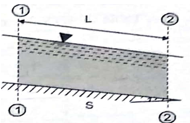
1) Rectangular section:
Consider rectangular channel of cross-sectional area A
Area of section A = By
Perimeter of section P = B + 2Y =  + 2y
+ 2y
Discharge through channel,
Q = A • v = AC 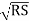
= AC 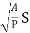
= C 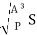
=  C
C 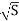
Since A, C, and S are constant in the above equation, the discharge will be maximum when perimeter P in minimum.
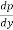 = 0
= 0
 (
(  + 2y) = 0
+ 2y) = 0
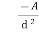 = 0
= 0
A = 2y2
By = 2y2
B = 2y
Y = 
The maximum discharge for the rectangular section occurs when depth is one – half of the width of the channel.
Hydraulic mean depth for this section
R =  =
= 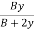
= 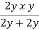 =
= 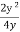
R = 
2) Trapezoidal section:
Consider a channel of trapezoidal cross-section
Let , A = are of cross-section
b = bottom width
y = depth of flow
 = side slope ( i.e. 1 vertical to m horizontal)
= side slope ( i.e. 1 vertical to m horizontal)
Area of section , A = ( b + my) y
b =  – my
– my
discharge Q = A • v = AC 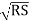
= AC 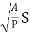
Since A, C, and S are constant in the above equation, the discharge will be maximum when perimeter P in minimum.
P = AB + BC + CD = b + 2(AB)
= b + 2 ( y 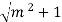 )
)
=  – my + 2y
– my + 2y 
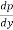 = 0
= 0
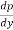 =
= 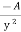 – m + 2
– m + 2 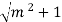 = 0
= 0
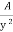 + m = 2
+ m = 2 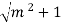
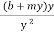 + m = 2
+ m = 2 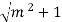
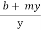 + m = 2
+ m = 2 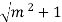
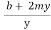 = 2
= 2 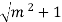
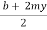 = y
= y 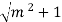
 (Top width) = Sloping side
(Top width) = Sloping side
Hydraulic mean depth for this section
R =  =
= 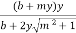
= 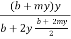
= 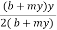
R = 
Best side slope for the trapezoidal channel for maximum discharge :
P =  – my + 2y
– my + 2y 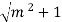
Maximum Discharge will be,
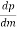 = 0
= 0
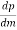 = - y + 2y x
= - y + 2y x  ( m2 + 1) -1/2 2m = 0
( m2 + 1) -1/2 2m = 0
- Y 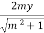 = 0
= 0
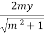 = 1
= 1
m2 + 1 = 4m2
3m2 = 1
m = 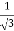
tan 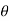 =
= 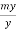 = m =
= m = 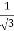
 = 30°
= 30°
Condition for economical cross-section,
 = y
= y 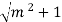
 = y
= y 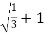
 +
+ 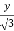 =
= 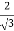 y
y
 =
= 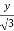
b = 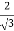 y
y
Perimeter P = b + 2y 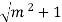
= 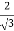 y + 2y
y + 2y 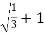
P = 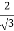 y +
y + 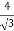 y =
y = 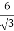 y =
y = 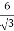 x
x  b = 3b
b = 3b
But, P = b + ( AB ) + CD = b + 2 ( AB)
3b = b + 2 ( AB)
AB = 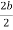 = b
= b
Sloping side of channel = Bed width of channel
3) Triangular section:
Consider a triangular section ABC

Let 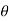 be the angle of each side with respect to vertical
be the angle of each side with respect to vertical
tan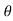 =
= 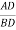 =
= 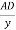
AD = DC = y tan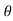
Top width AC = AD + DC = 2y tan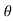
Area of section A =  x base depth =
x base depth =  ( 2y tan
( 2y tan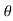 ) y
) y
A = y2 tan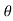 ………………………….eqn 1
………………………….eqn 1
Wetted perimeter P = AB + BC
= 2 (AB) = 2  = 2y
= 2y 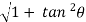
P = 2y 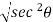 = 2y sec
= 2y sec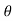 …………………eqn 2
…………………eqn 2
From equation 1, y = 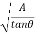
P = 2 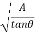 x sec
x sec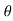
= 2 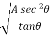
= 2 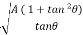
= 2 
For maximum discharge, the perimeter will be minimum,
 = 0
= 0
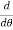 ( cot
( cot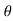 + tan
+ tan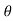 ) = 0
) = 0
Cosec2  + sec2
+ sec2  = 0
= 0
sec2 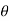 = Cosec2
= Cosec2 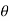
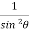 =
= 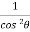
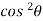 =
= 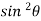
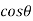 =
= 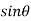
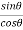 = 1
= 1
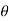 = 45°
= 45°
m = 1
From eqn 1, A = y2 tan45° = y2
Wetted perimeter P = 2y sec 45° = 2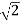 y
y
Hydraulic mean depth R =  =
= 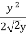 =
= 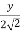
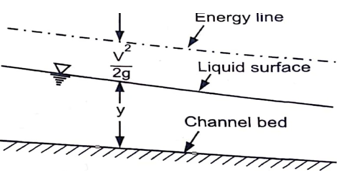
Specific Energy:
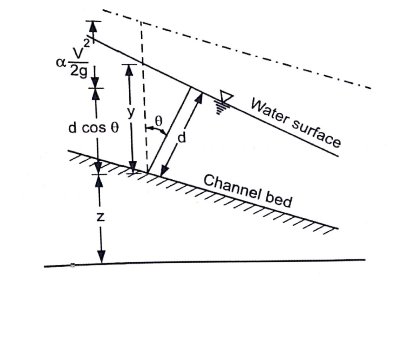
The total head (energy per unit weight) at any section with respect to any selected datum is given by
H = z + d cos 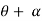
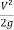 ..........................1
..........................1
Thus, from equation (1),
Specific energy E = d cos 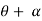
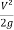 .................2
.................2
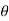
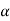
E = y + 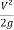 ........................3
........................3
The concept of specific energy.
Specific force:
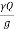
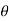
where y = unit weight of the liquid,
Q = discharge and
W = weight of liquid between sections 1-1 and 2-2. Ff force due to friction at the boundary of the channel. Force due to air resistance is neglected.
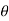
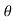
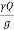 (V2-V1) = P1-P2 ...........................2
(V2-V1) = P1-P2 ...........................2
P1 = 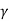 A1
A1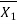 =
= A1
A1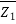
P2 =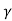 A2
A2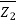
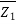
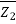
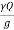 (V2-V1) =
(V2-V1) = 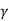 A1
A1 -
-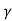 A2
A2
Q = A1V1 =A2V2 or V1= and V2=
and V2=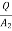
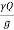 (
(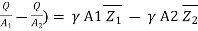
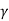
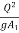 +
+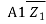 =
= 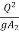 +
+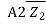 ..............................3
..............................3
F = + A
+ A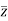 .................................4
.................................4
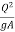
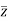
Depth - Discharge Diagram :
E= Y+ 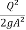
Q = 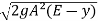
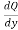
Q = 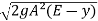 =
=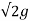 .A
.A 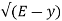
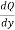
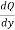 =
= 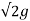 [
[ .
.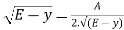 ]=0 .. . . .
]=0 .. . . . 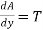
T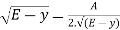 = 0
= 0
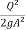

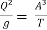 or
or 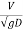 = 1 or Fr = 1
= 1 or Fr = 1
This is nothing but a condition for critical flow.
Critical Depth:
 = 0
= 0
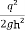
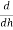 [ h +
[ h + 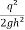 ] = 0 or 1 +
] = 0 or 1 +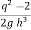 = 0
= 0
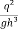 = 0 or 1 =
= 0 or 1 = 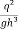 or h³ =
or h³ =
h =[ 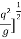
h c =[ 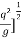
Condition of occurrence of critical flow:
1. Froude number is one (Fr = 1).
2. The velocity head is half the hydraulic depth of flow.
3. Specific force is minimum for a given discharge.
4. Discharge is maximum for a given specific force.
It is defined as the square root of the ratio of the inertia force and the gravity force.
Mathematically, 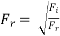
Froude number governs the similarity of the dynamics of the flow situations; where the gravitational force is more significant and all other forces are comparatively negligible.
Fr = 1, critical flow,
Fr > 1, supercritical flow (fast rapid flow),
Fr < 1, subcritical flow (slow / tranquil flow)
Critical Flow Criteria:conditions and characteristics
1)Specific energy is a minimum for a given discharge.
2) Discharge is a maximum for a given specific discharge
3) Specific force is a minimum for a given discharge.
4) Velocity head is equal to half the hydraulic depth in a channel of small slope.
5)Froude number is equal to unity.
6) Velocity of flow in a channel is equal to celebrity of small gravity waves in shallow water channel.
Section Factor-
The section factor for critical flow computation of achannel is the product of the water area and the square root of the hydraualic depth


Equation 1 & 2 are very useful for critical flow analysis.
Hydraulic exponent-
Since section factor is a function of the depth of flow y, and A may be assume that
Z=CyM
Where C is the coefficient and M is the parameter called hydraulic exponent for the critical flow.

Reference books:
1. Engineering Fluid Mechanics by R. J. Garde and A.J Mirajgaonkar, Pub: SCITECH Publications( India )Pvt.Ltd, Chennai
2. Fluid Mechanics and its Applications, Vijay Gupta, Santosh K Gupta, New Age International Pvt. Ltd, New Delhi,
3. Fluid Mechanics, Fundamentals, and applications by Yunus. A Cengel and John.M Cimbala, Mc Graw Hill International, New Delhi.
4. Fluid Mechanics by Streeter, Wylie, and Bedford – Pub: McGraw Hill International, New Delhi.
5. Open Channel Hydraulics by Ven Tee Chow, Pub: Mcgraw- Hill Book Company- Koga.
6. A Text-Book of Fluid Mechanics and Hydraulic Machines- by Dr. R K Rajput Pub: S Chand and Co Ltd. New Delhi