Unit 3
Dimensional Analysis and Model Studies & Boundary layer Theory
P = w h
Dimensions of LHS = ML-1T-2
Dimensions of RHS = ML-2T-2×L = ML-1T-2
Dimensions of LHS = Dimensions of RHS
Hence, equation P= w h is dimensionally homogeneous; so it can be used in any system of units.
Applications of Dimensional Homogeneity:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
 -------- 1
-------- 1
Equation 1 can also be written as
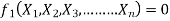 -------- 2
-------- 2
It is a dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it [eqn] can be written in terms of number of Π – terms in which the number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless 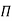 – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variables.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variables.
These m variables which appear repeated in each of 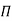 – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimensions and they do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimensions and they do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m(M, L, T) = 3, then each term is written as:
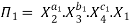
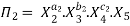
.
.
.
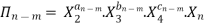 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2, etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and the values of 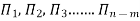 are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:


For geometric similarity to existing between the model and the prototype, the ratios of corresponding lengths in the model and the prototype must be the same and the included angles between the corresponding sides must be the same.
Models that are not geometrically similar are known as a geometrically distorted model.
Lm = length of model
Hm = height of the model
Dm = diameter of the model
Am = area of the model
Vm = volume of the model
And LP, BP, HP, DP, AP, and VP = corresponding values of the prototype.
Then, for geometric similarity, we must have the relation:
Where Lr is called the scale ratio or the scale factor:
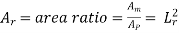
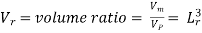
The kinematic similarity is the similarity of motion.
If at the corresponding points in the model and the prototype, the velocity or acceleration ratio is the same & velocity or acceleration vectors point in the same direction, the two flows are said to be kinematically similar.
(V1)m = velocity of the fluid at point 1 in the model.
(V2)m = velocity of the fluid at point 2 in the model,
(a1)m = acceleration of fluid at point 1 in the model
(a2)m = acceleration of fluid at point 2 in the model
And (V1)P, (V2)P, (a1)P (a2)P = corresponding values at the corresponding points of fluid, velocity, and acceleration in the prototype.
Then, for kinematic similarity, we must have
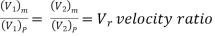
Similarly, 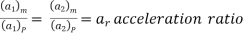
The direction of the velocities in the model and prototype should be the same.
The geometric similarity is a pre-requisite for kinematic similarity.
The dynamic similarity is the similarity of forces. The flows in the model and prototype are dynamically similar if, at all the corresponding points, identical types of forces are parallel and bear the same ratio.
In dynamic similarity, the force polygons of the two flows can be superimposed by a change in the force scale.
(Fi)m = inertia force at a point in the model,
(Fv)m = viscous force at the point in the model,
(Fg)m = gravity force at the point in the model
And (Fi)P, (Fv)P, (Fg)P = corresponding values of forces at the corresponding points in the prototype.
Then, for dynamic similarity we have
The direction of the corresponding forces at the corresponding points in the model and prototype should also be the same.
It is defined as the ratio of the inertia force to the viscous force.
Reynold’s Number, Re = 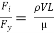
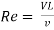
For pipe flow (where the linear dimension is taken as diameter d),
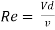
Reynold’s number signifies the relative predominance of the inertia to the viscous forces occurring in the flow systems.
It is defined as the square root of the ratio of the inertia force and the gravity force.
Mathematically, 
Froude number governs the similarity of the dynamics of the flow situations; where the gravitational force is more significant and all other forces are comparatively negligible.
It is defined as the square root of the ratio of the inertia force to the pressure force.
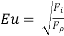
The Euler number is important in the flow problems/situations in which a pressure gradient exists.
It is defined as the square root of the ratio of the inertia force to the surface tension force.
Mathematically, 
This number assumes importance in the following flow situation:
i) The flow of blood in veins and arteries
ii) Liquid atomisation, and
iii) Capillary movement of water in soils
It is defined as the square root of the ratio of the inertia force to the elastic force.
Mathematically, 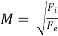
The Mach number is important in compressible flow problems at high velocities, such as high-velocity flow in pipes or motion of high-speed projectiles and missiles.
To ensure dynamic similarity between the model and prototype it is necessary that the ratio of the corresponding forces acting at the corresponding points in the model and prototype be made equal.
It implies that dimensionless numbers should be the same for the model as well as the prototype.
This condition is difficult to be satisfied with all the dimensionless numbers.
Hence models are designed based on the force which is dominating the flow situation. The laws on which the models are designed for dynamic similarity are called model or similarity laws; these are
Inflow situations where in addition to inertia, viscous force is the other predominant force, the similarity of flow in the model and its prototype can be established if Reynolds number is the same for both the systems.
This is known as Reynolds law and according to this law,

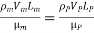
Where, ρm = density of the fluid in the model
Vm = velocity of the fluid in the model,
Lm = length of the linear dimension of the model, and
µm = viscosity of the fluid in the model
and ρP, VP, LP, and µP are the corresponding values of density, velocity, linear dimension, and viscosity of the fluid in the prototype.
Or 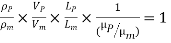
Or 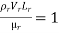
[ 
Following are some of the phenomenon for which Reynolds model law can be a sufficient criterion for similarity of flow in the model and the prototype:
When the gravitational force can be considered to be the only predominant force that controls the motion in addition to the inertia force, the similarity of the flow in any two such systems can be established if the Froude’s number of both the systems is the same.
This is known as Froude’s Model Law.
Some of the phenomenon for which the Froude Model Law can be sufficient criterion for dynamic similarity to be established in the model and the prototype are:
Let, Vm = velocity of the fluid in the model
Lm = length (or linear dimension) of the model
gm = acceleration due to gravity (at a place where the model is tested)
and VP, LP, and gP are the corresponding values of the velocity, length, and acceleration due to gravity for the prototype.
Then according to Froude Law,
(Fr)m = (Fr)P
Or 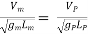 ------ 1
------ 1
As the value of g at the site of mode testing will be practically the same as at the site of the proposed prototype, therefore gm = gP and the equation 1 values as
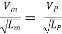
Or 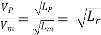
Where Lr = scale ratio for length
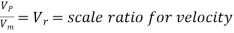

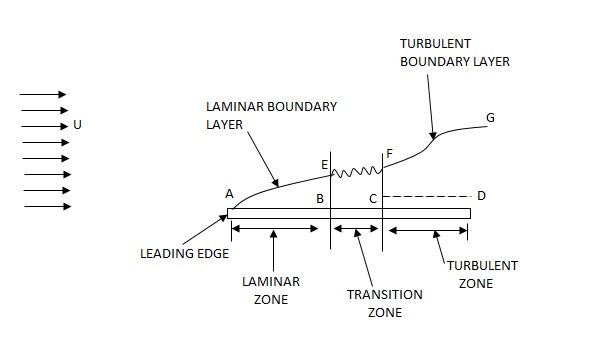
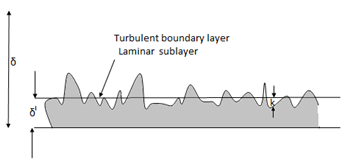
Laminar and turbulent boundary layer
Laminar Boundary Layer
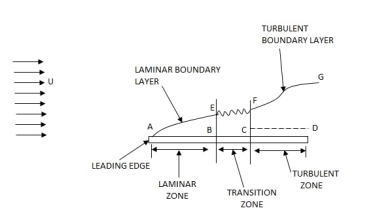
Turbulent Boundary Layer
Boundary-Layer Thickness (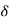 )
)
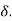
1. 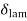 = Thickness of laminar boundary layer,
= Thickness of laminar boundary layer,
2. 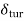 = Thickness of turbulent boundary layer, and
= Thickness of turbulent boundary layer, and
3. 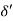 = Thickness of laminar sublayer.
= Thickness of laminar sublayer.
Displacement Thickness(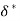 )
)
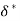
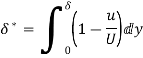
Momentum Thickness (
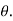

Energy Thickness ( )
)
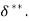
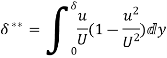

Local coefficient of drag (CD*)
It is defined as the ratio of the shear stress 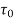 to the quantity
to the quantity 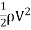
It is denoted by CD*
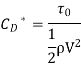
The average coefficient of Drag (CD)
It is defined as the ratio of total drag force to the quantity 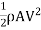
It is also called the coefficient of drag and is denoted by CD.
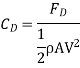
where A= area of the surface (or plate)
V = free stream velocity
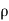 = mass density of fluid
= mass density of fluid

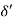
i) Hydrodynamically smooth boundary, when ( ) < 0.25
) < 0.25
ii) Hydrodynamically rough boundary, when ( ) > 6.0
) > 6.0
iii) Boundary in transition, when 0.25 < ( ) < 6.0
) < 6.0
Separation of boundary layer
Methods of preventing the separation of the boundary layer
The following are the methods of preventing the separation of the boundary layer:
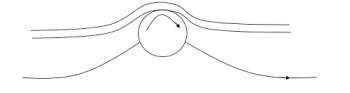
By rotating a circular cylinder lying in a stream of fluid so that the upper side of the cylinder where the fluid, as well as the cylinder, move in the same direction, the boundary layer does not form.
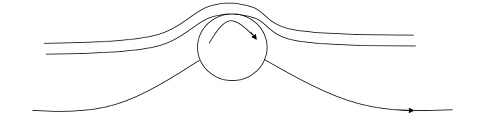
2. Acceleration of fluid in the boundary layer:
This method of controlling separation consists of supplying additional energy to particles of fluid which are being retarded in the boundary layer. This may be achieved either by injecting the fluid into the region of the boundary layer from the interior of the body with the help of some available device as shown in the figure or by diverting a portion of fluid of the mainstream from the region of high pressure to the retarded region of boundary layer through a slot provided in the body.
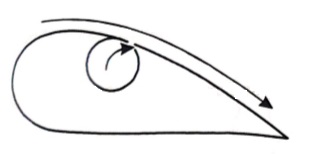
3. The suction of fluid from the boundary layer:
In this method, the slow-moving fluid in the boundary layer is removed by suction through slots or a porous surface as shown in the figure.

4. Streamlining of the body shapes:
By the use of suitably shaped bodies, the point of transition of the boundary layer from laminar to turbulent can be moved downstream which results in the reduction of the skin friction drag. Furthermore, by streamlining the body shapes the separation may be eliminated.
5. Supplying additional energy from a blower.
6. Rotating boundary in the direction of flow.
7. Providing small divergence in a diffuser.
8. Providing guide blades in a bend.
9. Providing a tripwire ring in the laminar region for the flow over a sphere.
Reference books:
1. Engineering Fluid Mechanics by R. J. Garde and A.J Mirajgaonkar, Pub: SCITECH Publications( India )Pvt.Ltd, Chennai
2. Fluid Mechanics and its Applications, Vijay Gupta, Santosh K Gupta, New Age International Pvt. Ltd, New Delhi,
3. Fluid Mechanics, Fundamentals, and applications by Yunus. A Cengel and John.M Cimbala, Mc Graw Hill International, New Delhi.
4. Fluid Mechanics by Streeter, Wylie, and Bedford – Pub: McGraw Hill International, New Delhi.
5. Open Channel Hydraulics by Ven Tee Chow, Pub: Mcgraw- Hill Book Company- Koga.
6. A Text-Book of Fluid Mechanics and Hydraulic Machines- by Dr. R K Rajput Pub: S Chand and Co Ltd. New Delhi