Unit 1
Properties of Fluids & Fluid Statics
A fluid may be defined as follows :
“A fluid is a substance that is capable of flowing.”
Fluid Mechanics:
Fluid Mechanics may be defined as that branch of engineering science which deals with the behavior of fluid under the conditions of rest and motion. Fluid mechanics may be divided into three parts: Statics, Kinematics, and dynamics.
Statics: The study of incompressible fluids under static conditions is called hydrostatics and that dealing with the compressible static gases is termed as aerostatics.
Kinematics: It deals with the velocities, accelerations, and the patterns of flow only. Forces or energy causing velocity and acceleration are not dealt with under this heading.
Dynamics: It deals with the relations between velocities accelerations of fluids with the forces or energy causing them.
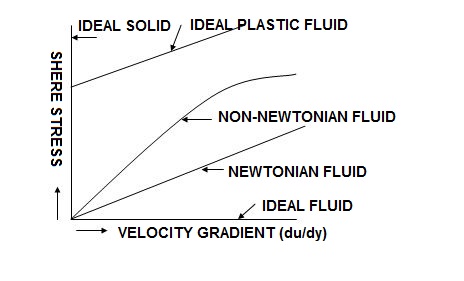
Ideal Fluid: A fluid which is incompressible and is having no viscosity, is known as an ideal fluid. Ideal Fluid is only an imaginary fluid as all the fluids. which exist have some viscosity.
Real Fluid: A fluid, which possesses viscosity, is known as real fluid. All the fluids in actual practice are real fluids.
Rheological Diagram
Density or Mass Density:
The density or mass density of a fluid is defined as the ratio of the mass of a fluid to its volume.
It is denoted by the symbol (rho).
The unit of mass density in the SI unit is kg/m3.
= Mass of fluid / Volume of fluid = m/v
The value of the density of water is 1000 kg/m3
Specific weight or weight density:
Specific weight or weight density of a fluid is the ratio between the weight of a fluid to its volume.
It is denoted by the symbol w.
w = Weight of fluid / Volume of fluid = W/v
= x g
The value of specific weight or weight density(w) for water is 9810N/m3.
Specific Volume:
Specific Volume of a fluid is defined as the volume of a fluid occupied by a unit mass or volume per unit mass of a fluid is called as specific volume.
Mathematically, it is expressed as,
Specific Volume = Volume Of Fluid / Mass of Fluid = v/m
= 1/
It is expressed as m3 /kg.
Relative density or Specific Gravity :
Specific Gravity is defined as the ratio of the weight density of a fluid to the weight density of the standard fluid.
Specific gravity is also called relative density. It is dimensionless gravity and is denoted by the symbol S.
S (For Liquids ) = Weight density(density) of liquid / Weight density(density) of Water.
The specific gravity of mercury is 13.6 and the specific gravity of water is 1.
Viscosity:
Newton’s Law of Viscosity
This law states that the shear stress () on a fluid element layer is directly proportional to the rate of shear strain. The constant of proportionality is called the coefficient of viscosity.
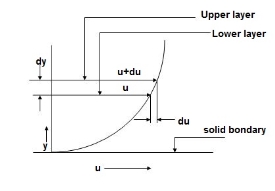
= du / dy
The fluids which follow this law are known as Newtonian fluids.
Viscosity may be defined as the property of the fluid which determines its resistance to shearing stresses. It is a measure of the internal fluid friction which causes resistance to flow.
The viscosity of fluids is due to cohesion and interaction between particles.
du/dy
= du/dy
= Constant of proportionality and is known as co-efficiency of dynamic viscosity.
du/dy = Rate of shear stress or the rate of shear deformation or velocity gradient.
We have,
= / [du/dy]
Thus, the viscosity may also be defined as the shear stress required to produce a unit rate of shear strain.
Units of Viscosity:
In S.I.units : N.s/m2
Kinematic Viscosity :
Kinematic Viscosity is defined as the ratio between the dynamic viscosity and density of the fluid. It is denoted by v (called nu).
v = Viscosity / Density
= /
Units of Kinematic Viscosity :
In SI units: m2/s
Compressibility The property under which fluids undergo a change in volume under the action external pressure is known as compressibility. It decreases with the increase in the pressure of the fluid.
The bulk modulus of elasticity (K) is defined as the ratio of compressive stress to volumetric strain. Compressibility is the reciprocal of bulk modulus of elasticity.
Cohesion: Cohesion means intermolecular attraction between molecules of the same liquid. It enables a liquid to resist a small number of tensile stresses. Cohesion is a tendency of the liquid to remain as one assemblage of particles.
Adhesion: Adhesion means attraction between the molecule of a liquid and the molecule of a solid boundary surface in contact with the liquid. This property enables a liquid to stick to another body.
Surface tension is caused by the force of cohesion at the free surface.
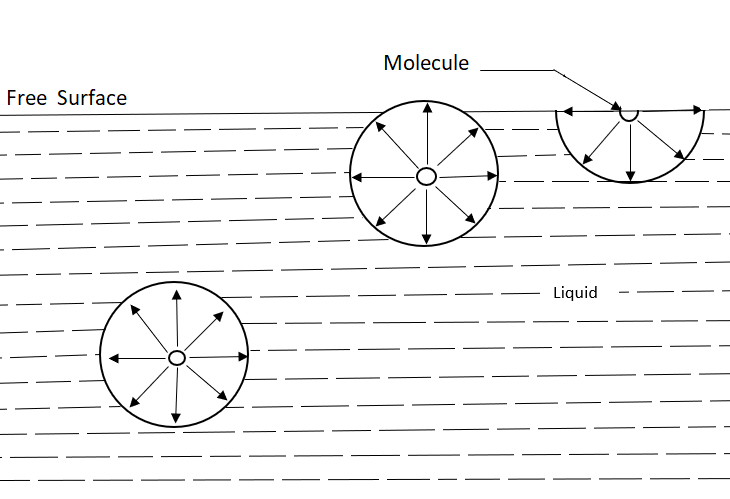
A liquid molecule in the interior of the liquid mass is surrounded by the other molecules all around and is in equilibrium.
At the free surface of the liquid, there are no liquid molecules above the surface to balance the force of the molecules below it.
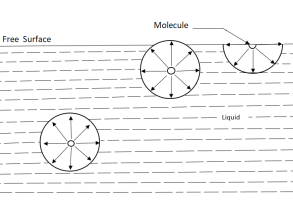
Consequently, as shown in fig there is the net inward force on the molecules at the free surface.
The force is normal to the liquid surface.
At the free surface, a thin layer of molecules is formed.
It is denoted by letter .
It’s SI unit is N/m.
Capillarity is defined as a phenomenon of rising or fall of a liquid surface in a small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid.
The rise of liquid surface is known as capillary rise while the fall of the liquid surface is known as capillary depression.
It is expressed in terms of cm or mm of liquid.
Its value depends upon the specific weight of the liquid, the diameter of the tube, and the surface tension of the liquid.
h = Height of the liquid in the tube.
d = Diameter of tube
= Surface tension of liquid.
= Angle of contact between liquid and glass tube.
= Density Of liquid.
h= 4cos / e*g*d
All liquid tends to evaporate a vaporize.
Molecules are continuously projected from the free surface to the atmosphere.
These ejected molecules are in a gaseous state and exact their own partial vapor pressure on the liquid surface. This pressure is known as the vapors' pressure of the liquid (Pv).
Vapors pressure increase with the rise in temperature.
To determine the pressure at any point in a fluid at rest ‘hydrostatic law ‘ is used which states that ‘the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.
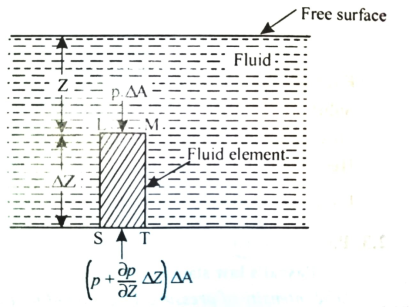
Let p = Intensity of pressure on face LM,
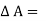 Cross-sectional area of the element,
Cross-sectional area of the element,
Z = Distance of the fluid element from the free surface,
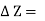 Height of the element,
Height of the element,
The forces acting on the elements are:
Pressure forces on the face LM = p x 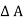 …….acting downward.
…….acting downward.
Pressure forces on the face ST = 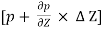 x
x 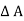 ……. Acting upward
……. Acting upward
Weight of the fluid element = Weight density x Volume
= w x 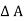 x
x 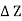
Pressure forces on the face MT & LS are equal and opposite.
For equilibrium of the fluid element,
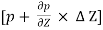 x
x 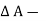 p x
p x 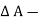 w x
w x 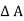 x
x 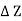 = 0
= 0
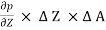 - w x
- w x 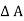 x
x 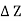 = 0
= 0
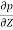 = w
= w
Above eqn states that the rate of increase of pressure in a vertical direction is equal to the weight density of the fluid at that point. This is hydrostatic law.
On integrating above eqn
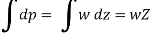
where p = pressure above atmospheric pressure
Z = pressure head.
w = Specific weight of liquid.
Pressure always acts inward normal to any surface (even imaginary surfaces as in a control volume).
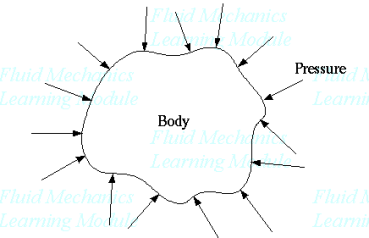
Pressure is a normal stress, and hence has dimensions of force per unit area, or {ML-1T-2}. In the English system of units, pressure is expressed as "psi" or lbf/in2.
In the Metric system of units, pressure is expressed as "pascals" or N/m2.
Standard atmospheric pressure is 101.3 kPa (0.1013 MPa) or 14.69 psi.
To determine the pressure at any point in a fluid at rest ‘hydrostatic law ‘ is used which states that ‘the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.
p = w Z
or
Z
where p = pressure above atmospheric pressure
Z = pressure head.
w = Specific weight of liquid.
Pascal's law states that the pressure applied to a fluid in a closed container is transmitted equally to all points in the fluid and acts in all directions of the container. It is applicable to both solids and liquids.
Aplication of pascal’s law-
Imp points of pascal law-
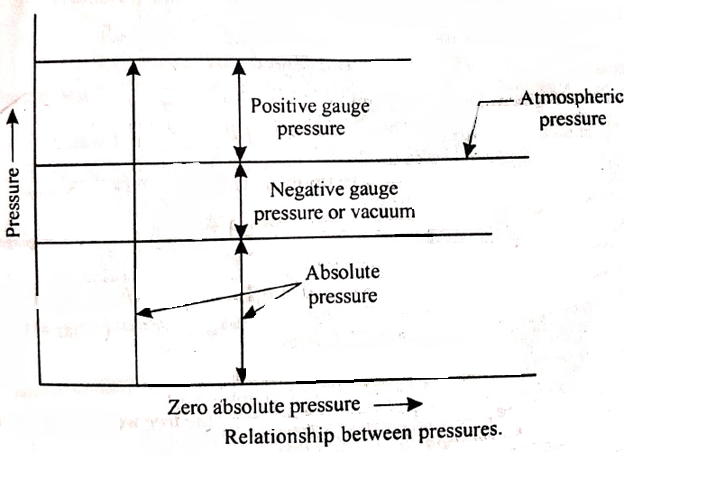
It is the pressure, measured with the help of a pressure measuring instrument, in which the atmospheric pressure is taken as a datum.
The atmospheric pressure on the scale is marked as zero.
It is necessary to establish an absolute pressure scale that is independent of the changes in atmospheric pressure.
A pressure of absolute zero can exist only in a complete vacuum.
Any pressure measured above the absolute zero of pressure is termed as an absolute pressure.
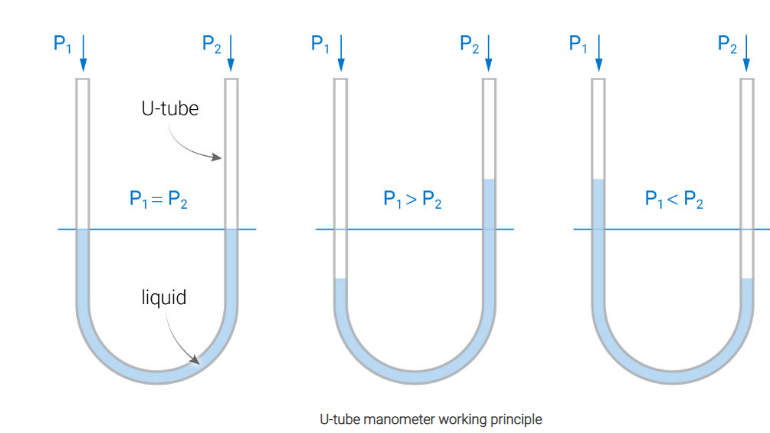
Principle of manometers
Hydrostatic equilibrium shows that the pressure when a liquid is at rest is equal at any point.
For example, if both ends of the U-tube are left open to the atmosphere then the pressure on each side will be equal. As a consequence the level of the liquid on the left-hand side will be the same as the level of the liquid on the right-hand side – equilibrium. However, if one end of the U-tube is left open to the atmosphere and the other connected to an additional gas/liquid supply this will create different pressures.

Balancing liquid column
Manometers measure a pressure difference by balancing the weight of a fluid column between the two pressures of interest. Large pressure differences are measured with heavy fluids, such as mercury (e.g. 760 mm Hg = 1 atmosphere).
Small pressure differences, such as those experienced in experimental wind tunnels or venturi flowmeters, are measured by lighter fluids such as water (27.7 inch H2O = 1 psi; 1 cm H2O = 98.1 Pa).

Pressure transducers
A pressure transducer is used to convert a certain value of pressure into its corresponding mechanical or electrical output. Measurement if pressure is of considerable importance in process industries.
The types of pressure sensors are differentiated according to the amount of differential pressure they are able to measure.
For low differential pressure measurement Liquid Column Manometers are used. Elastic type pressure gauges are also used for pressure measurement up to 700 MPa.
Types:
The manometer is defined as the devices used for measuring the pressure at a point in a fluid by balancing the column of fluid by the same or another column of liquid.
A “simple manometer” is one which consists of a glass tube whose one end is connected to a point where pressure is to be measured and the other end remains open to atmosphere.
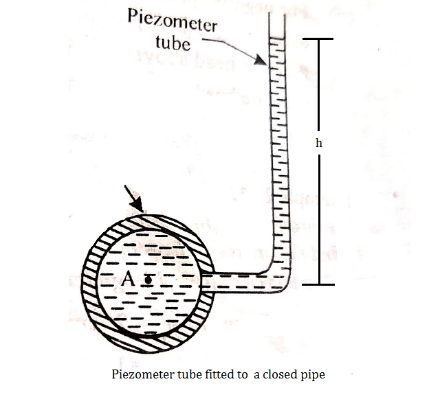
i) Piezometer:
ii) U-tube manometer:
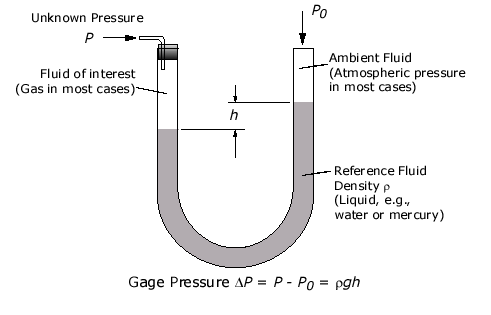
Fig (a) Fig (b)
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in the pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above the X-X line in the left limb = h+h1S1
Pressure head above the X-X in the right limb = h2S2
Equating these two pressures, we get
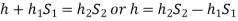
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb= 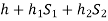
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
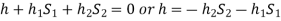
iii) Inclined Single Column Manometer:
l = length of the heavy liquid moved in right limb,
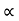 = inclination of right limb horizontal, and
= inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin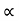
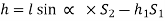

A differential manometer is used to measure the difference in pressures between two points in a pipe or two different pipes.
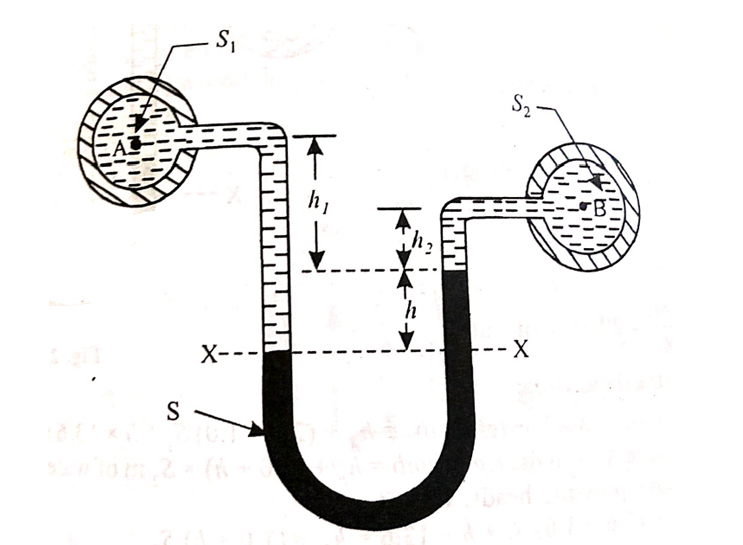
i) U-tube differential manometer:
A U-tube differential manometer is shown in fig.
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the center of A, from the mercury level in the left limb
h2 = distance of the center of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
hA = pressure head at A,
hB = pressure head at B
considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
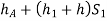
Pressure head in the right limb:

Equating the above pressure heads, we get
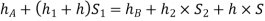
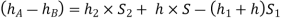
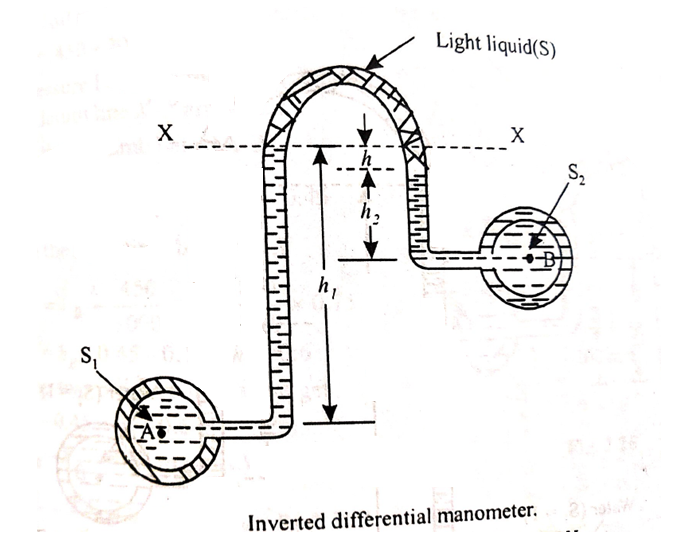
ii) Inverted U-tube differential manometer:
An inverted U-tube differential manometer is shown in fig.
It consists of an inverted U tube, containing light liquid, whose two ends are connected to the points whose difference pressures are to be measured.
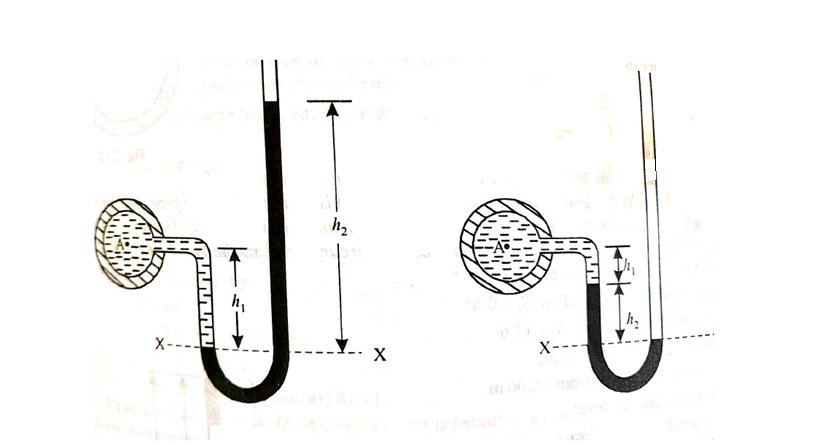
Let, h = difference of mercury level (light liquid) in the U-tube,
h1 = Height of liquid in the left limb below the datum line X-X
h2 = Height of liquid in the right limb below the datum line X-X
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of the light liquid
hA = pressure head at A,
hB = pressure head at B
considering the pressure heads below the datum line x-x, we get
Pressure head in the left limb:
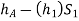
Pressure head in the right limb:
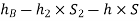
Equating the above pressure heads, we get
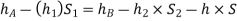
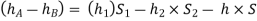
Total Pressure
The total pressure is defined as the force exerted by a static fluid on a surface either plane or curved when the fluid comes in contact with the surfaces. This force always acts normal to the surface.
Centre of Pressure
The Centre of pressure is defined as the point of application of the total pressure on the surface. There are four cases of submerged surfaces on which the total pressure force and center of pressure are to be determined. The submerged surfaces may be:
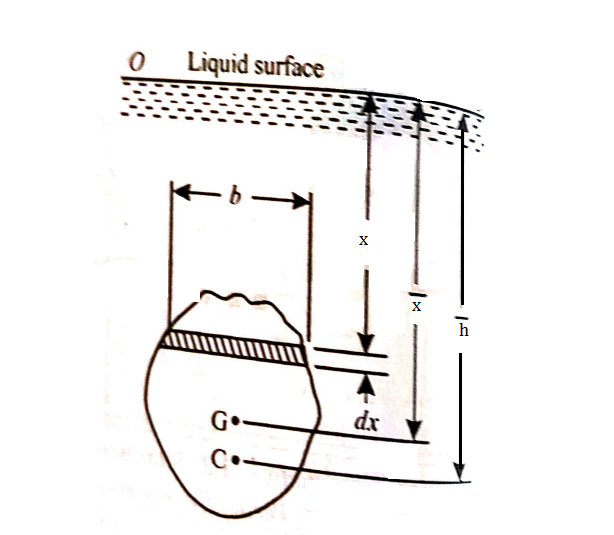
Consider a thin horizontal strip of the surface of thickness dx and breadth b.
Let the depth of the strip be x.

Let the intensity of pressure on strip be p.
p =wx
Total pressure on the strip = p.bdx = wx.bdx
Total pressure on the whole area P =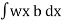
=w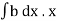
But 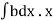 = Moment of the surface area about the liquid level = A
= Moment of the surface area about the liquid level = A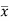
P=wA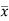
Moment of the pressure about free surface OO = (w.x.b. dx).x = w.x2.b.dx
Total Moment, M = 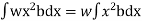
But 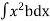 = Moment of inertia of the surface about free surface OO (I0)
= Moment of inertia of the surface about free surface OO (I0)
Hence, M = wI0
The sum of the moment of the pressure is also equal to P×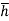 .
.
P×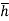 = wI0
= wI0
wA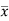 x
x 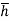 = wI0
= wI0
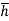 =
= 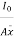
But 
Above eqn becomes
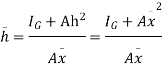
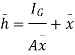
2. Horizontal plane surface
The total pressure on a horizontally immersed surface, as shown in Fig.above, is given by
where
w = Specific weight of the liquid,
A = Area of the immersed surface, and
x (bar) = Depth of the centre of gravity of the immersed surface from the liquid surface.
3. Inclined plane surface
Let A = area of the surface
 = depth of the center of gravity from the free liquid surface.
= depth of the center of gravity from the free liquid surface.
 =angle at which the immersed surface is inclined with the liquid surface.
=angle at which the immersed surface is inclined with the liquid surface.
w=specific weight of liquid.
Consider a strip of thickness dx width b at a distance l from O.
The intensity of pressure on the strip = wlsin
Area of strip = b.dx
Pressure on the strip =Intensity of pressure × area = wlsin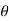 × b.dx
× b.dx
The total pressure on the surface
P = 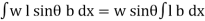
But 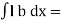 Moment of surface about OO =
Moment of surface about OO = 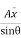
P=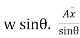 = w.
= w.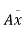
Let, 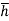 = Depth of center of pressure below the free liquid surface
= Depth of center of pressure below the free liquid surface
IG = Moment of inertia of the immersed surface about 00.
Moment of pressure about OO = wl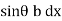 × l = wl2
× l = wl2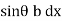
Sum of moments about O
M = 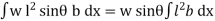
But 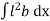 = I0 = Moment of inertia of the surface about point O
= I0 = Moment of inertia of the surface about point O
M = 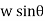 Io
Io
Sum of the moment of all such pressure about O is also equal to 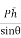
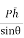 = w
= w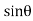 Io
Io
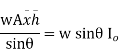
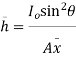

Where 
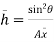 (
(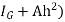
=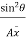 (
(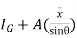 2)
2)
=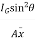 +
+ 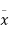
4. Curved surface
Consider a curved immersed surface LM submerged in a static fluid as shown in fig.
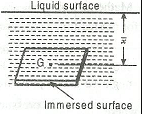
At any point on the curved surface, the pressure acts normal to the surface.
Thus, if dA is the area of a small element of the curved surface lying at a vertical depth of h from the surface of the liquid, then total pressure on the elemental area is

This force dP acts normal to the surface. Further integration of the above eqn would provide the total pressure on the curved surface and hence
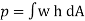
But in the case of a curved surface, the direction of the total pressure on the elementary areas is not in the same direction but varies from point to point.
Thus, the integration of eqn. for the curved surface is impossible. The problem, however, can be solved by resolving the force P into horizontal and vertical components PH and PV. Then total force on the curved surface is
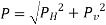
Hence, the direction of the resultant force P

Where,
PH = Total pressure force on the projected area of the curved surface on the vertical plane.
PV = Weight of the liquid supported by the curved surface of the liquid.
Practical applications
Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force that tends to lift it up.
The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to the action of gravity is known as buoyancy.
The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
The magnitude of the buoyant force can be determined by the Archimedes principle which states as follows :
“ When a body is immersed in fluid either wholly or partially it is buoyed or lifted by a force which is equal to the weight of the fluid displaced by the body. ”
Centre of Buoyancy
The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Stability of floating Body :
The stability of a floating body is determined from the position of Meta-centre (M).
a) Stable Equilibrium
If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
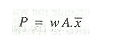
M is above G (stable equilibrium) M is below G (unstable equilibrium)
If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
b) Unstable Equilibrium :
If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
The disturbing couple is acting in the clockwise direction.
The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
c) Neutral Equilibrium :
If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
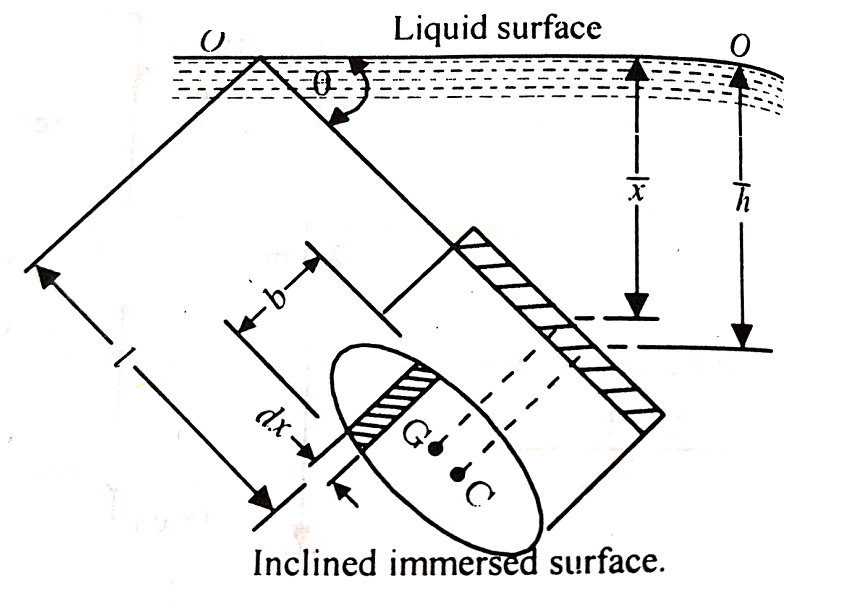
Stability of submerged Body :
The position of the center of gravity ¢er of buoyancy in case of a completely submerged body is fixed.
Weight W acting vertically downward through G, while the buoyant force FB is acting vertically up through B.
Stable Equilibrium
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium :
If W = FB , but the center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium :
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Reference books:
1. Engineering Fluid Mechanics by R. J. Garde and A.J Mirajgaonkar, Pub: SCITECH Publications( India )Pvt.Ltd, Chennai
2. Fluid Mechanics and its Applications, Vijay Gupta, Santosh K Gupta, New Age international Pvt. Ltd, New Delhi,
3. Fluid Mechanics, Fundamentals, and applications by Yunus. A Cengel and John.M Cimbala, Mc Graw Hill International, New Delhi.
4. Fluid Mechanics by Streeter, Wylie, and Bedford – Pub: McGraw Hill International, New Delhi.
5. Open Channel Hydraulics by Ven Tee Chow, Pub: Mcgraw- Hill Book Company- Koga.
6. A Text-Book of Fluid Mechanics and Hydraulic Machines- by Dr. R K Rajput Pub: S Chand and Co Ltd. New Delhi