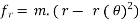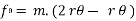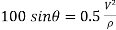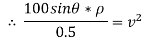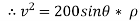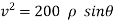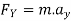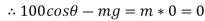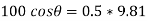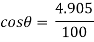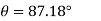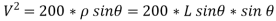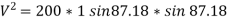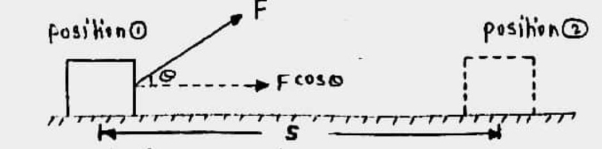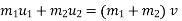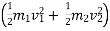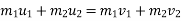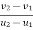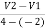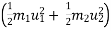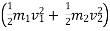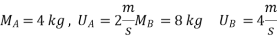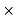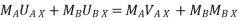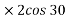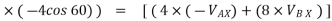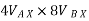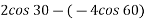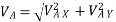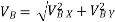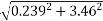UNIT 6
Kinetics of Particle
Motion of the body by considering the force causing motion.
OR
Motion of the bodies under the action of unbalanced force acting on it.
Newton’s law: -
Everybody continues in state of rest or state of uniform motion unless it is acted by some external force.
Newton’s second law: -
The rate of change of momentum is directly proportional to the impressed force and take place in direction of force.
- F = m.a
Newton’s third law :-
To every action there is equal and opposite reaction.
Application of newton’s second law :-
1) For rectangular coordinate system :-
When unbalanced force is acting on particle having acceleration “ a ”
Then by newton’s second law we can write
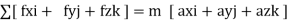
∑ 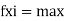
∑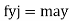
∑
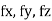 = are the forces acting along I , j , k.
= are the forces acting along I , j , k.
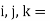 direction along
direction along 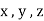 .
.
 components of acceleration “ a ” acting in
components of acceleration “ a ” acting in 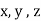
Direction or acting in 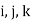 direction.
direction.
2) Application of second law for curvilinear motion of particle ( using tangential and normal component ) :-
then,
According to newton’s second law
∑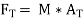
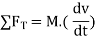
3) Application of second law for radial and transverse coordinates :-
When particle move along curve and number of forces are acting on it.
Then,
According to second law
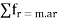
The force of equal magnitude but acting in the opposite direction of motion us called inertia of force.
Inertia force can keep the particle in equilibrium.
D’- ALEMBERT’S PRINCIPLE :-
It states that the sum of external force acting on a body and inertia force is always equal to zero.
∑
- For rectilinear motion
∑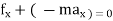 or ∑
or ∑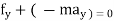
2. For universal motion
∑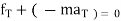 Or
Or
∑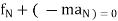
D’-ALMBERTS Principle for universal motion :-
D’-ALMBERTS Principle for universal motion in Cartesian coordinates:-
∑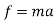
∑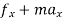
∑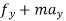
∑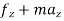
D’-ALMBERTS principle for curvilinear motion in path variables ( tangential and normal coordinates ) :-
∑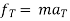 AND ∑
AND ∑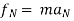
∑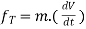 AND ∑
AND ∑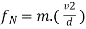
For radial and transverse coordinates :-
∑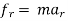 AND ∑
AND ∑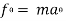
Therefore,
∑
|
NUMERICALS ON D’-ALEMBERTS PRINCIPLE FOR CURVILENAR MOTION
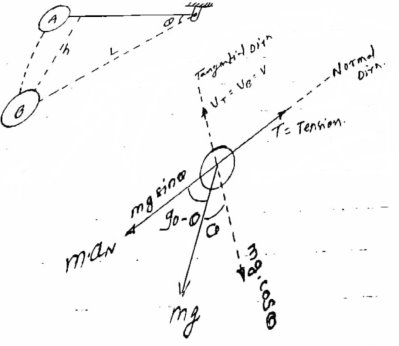
1} A pendulum bob has a mass of 10 kg and released from rest when  as shown in fig. determine the tension in the chord at
as shown in fig. determine the tension in the chord at 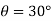 . Neglect the size of bob. ( dec- 15 )
. Neglect the size of bob. ( dec- 15 )
|
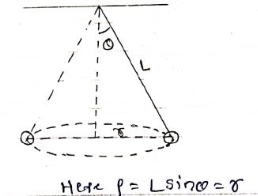
h = L sin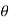
consider the pendulum is initially at A and when it is released it occupies new position at B.
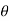 = angle displaced
= angle displaced
L = Length of string of pendulum = radius of curvature = 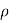 {rho}
{rho}
Now at point B apply D’- Alemberts Principle in normal direction ∑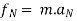
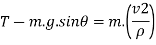
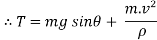
Here,
V = velocity at B = 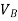
 Using equation of motion
Using equation of motion
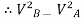 = 2gs
= 2gs
∴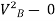 = 2gh
= 2gh

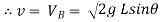
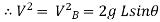 ……….. put in equation 1
……….. put in equation 1
We get,
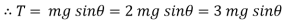
At
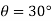
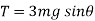
 N
N
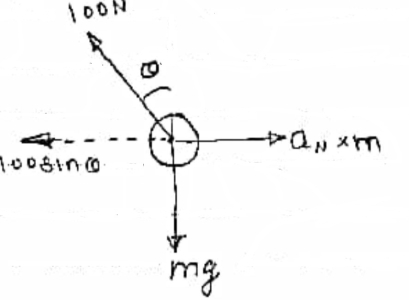
2} A 0.5 kg balls revolves in horizontal circle as shown in figure. If L = 1m and maximum allowable tension in the string is 100N determine maximum allowable speed and corresponding angle  .
.
Consider the body diagram of ball as shown in figure
Apply D’-ALEMBERTS principle in x direction
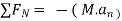
|

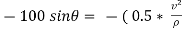 )
)
|
∴
Apply D’- alemberts principle in y direction \ ∑ But as there is no velocity in y direction thus
Therefore, V= 14.12 m/s This is max allowable speed.
|
WORK ENERGY PRINCIPLE
Work and work done :-
The work is said to be done when a force acts on a body and moves through certain distance.
W.D = Force * distance
U = F * S
Unit of work done
n.m or Joule (J)
If body dose not move in one direction of force then
W.D = Component of force in the direction of motion * displacement or distance.
Work done by external force :-
A}
|
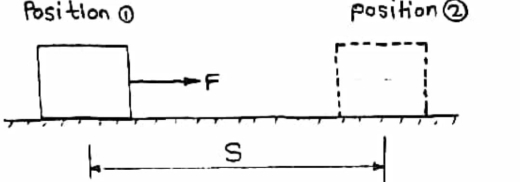
Consider an object at position (1) and subjected to force “ f ” .
Due to force f and object will be displaced from the position (1) to new position (2) at a distance ‘ s ’. then work done is given as
W.D = force * displacement
U = F * S ………. ( +ve if w.d is in the direction of the force )
B]
|
If an object is subjected to a force ‘ F ’ acting at an angle 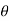 with horizontal, then object is displaced from position (1) to position (2) at distance ‘ s ’. here the work is done due to component of force in direction of motion ( displacement).
with horizontal, then object is displaced from position (1) to position (2) at distance ‘ s ’. here the work is done due to component of force in direction of motion ( displacement).
W.D = U = component of force in direction of displacement * displacement .
U = fcos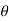 * s
* s
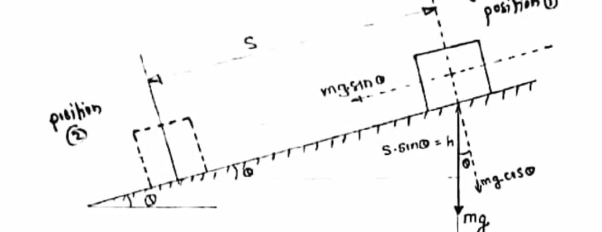
Work done by gravitational force gravity :-
|
As shown in figure if object of mass ‘ m ’ is displaced from position (1) to position (2) then W.D IS given by ,
W.D = weight * displacement in the direction of weight.
U = m.g * h
U = m.g.s sin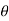
Therefore,
U = mg sin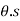
If block is moving from (1) to (2) i.e in the down direction ( in the direction of the gravity ) then W.D is +ve.
If block is moving from position (2) to (1) then it is against the gravity , so W.D is negative (-ve)
U = -mg sin .s
.s
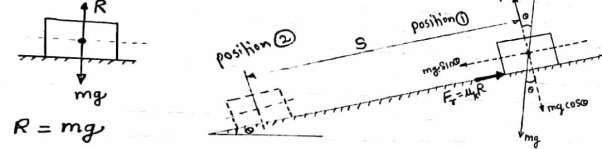
Work done due to fractional force :-
|
R=Normal Reaction
R=mg for horizontal plane
R=mg cos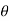 for inclined plane
for inclined plane
 Fraction force= Fr=Uk
Fraction force= Fr=Uk
 W.D.by friction force = Friction force
W.D.by friction force = Friction force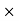 displacement
displacement
 U=
U= 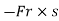
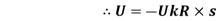
Uk= coefficient of kinetic friction
*Friction force(Fr) always act in the opposite direction of displacement .
Thus W.D is negative.
:W.D.by friction force is always negative .
:Use coefficient of kinetic friction Uk .
:when object is moving on the horizontal plane then,
R= mg cos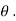
When object is moving on the inclined plane ,then
R= mg. cos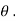
Wrock done by spring force
|
Consider spring with stiffness k as soon in figure with under formed length .
Let X1 = deformation of spring at position 1 of an object .
X2 = deformation of spring at position 1 of on object .
Then
Spring force = F=k.x

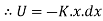
= 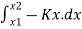
= 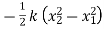
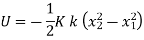
K : spring constant or stiffness = unit (N/m)
-ve sign indicates that spring force acts in the direction opposite to displacement
i.e. towards original position .
* Energy * (energy of a partial)
The capacity to do work is called as energy .
It is scaler quantity.
Type of energy : 1] Mechanical energy – potential energy .
- Kinetic energy .
2] Thermal energy .
3] Electrical energy .
Potential energy :-
The energy possessed by a partial by virtue of its position is known as potential energy.
P.E.=m.g.h.
Kinetic energy :-
The energy possessed by a partial due to its motion is called kinetic energy .
K.E. = 1/2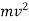 .
.
Work energy principal :-
It state that “ The total work done by all the forces acting on the partical during some displacement is equal to change in kinetic energy during that displacement .
From newton second law,
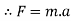
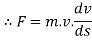
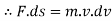
Integrate both side
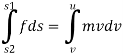
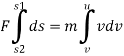
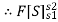 = m.
= m.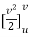
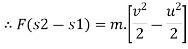
But s2-s1= s
F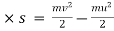
& F 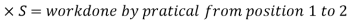
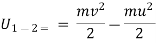
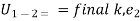 – intial k.
– intial k.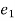
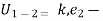 k.
k.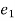
 change in kinetic energy.
change in kinetic energy.
k. = kinetic energy of partical at postion 1
= kinetic energy of partical at postion 1
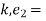 kinetic energy of partical at position 2
kinetic energy of partical at position 2
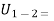 algebraic sum of w.d. by all force acting on the partical
algebraic sum of w.d. by all force acting on the partical
Conservative force :-
If work done by a force is independent of the path followed by partical , then a force is known as conservation force .
Here w.d.=change of potential energy of practical.
Ex. spring force , gravity force etc.
non conservative force :-
ifw.d . by a force is dependent upon the followed by partical , then force is called as non-conservation force .
 k.
k.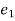
ex. fractional force , viscous force etc.
Principal of conservation of Energy :-
It states that “ The total energy of a partical [P.E+ K.E.] remain constant during the displacement of partical from position 1 to position 2 under the action of conservation force .
Fron work energy principal :-
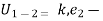 k.
k.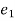 ____1
____1
But
Under the action of conservation force ,
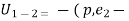 p.
p.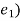 _____2
_____2
Equating 1&2
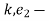 k.
k.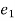 = -
= -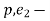 p.
p.
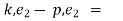 k.
k. p.
p.
 =
= 
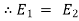 where,
where,
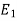 = k.
= k. p.
p.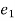 = total energy of position 1
= total energy of position 1
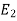 =
= 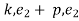 = total energy of position 2
= total energy of position 2
Where principal are involved , then above principal cannot be used .
Power:-
It is rate doing work.
Power = 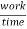
Power = 
Power = force 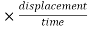
Power = force 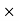 velocity .
velocity .
Power 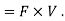
Efficiency :-
The ratio of work done by machine to the work done on the machine same time is called as efficiency .
 Outout power / Input power.
Outout power / Input power.
Impulse momentum theorem directly related force , velocity and time . the theorem is useful where force act very small intervals
- Important terms :-
1] Linear momentum :-
It is the total quantity of motion possess by a body or partical or object.
Linear moventum = mass 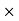 velocity
velocity
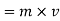 .
.
S.I. unit :-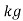 .m/sec
.m/sec
2] Angular moventum :-
It is the product of mass moment of intertia of the body (I) and angular velocity of the body.
Angular movement= mass moment of inertia 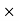 angular speed
angular speed
Angular movement = Iw
SI unit is :- kg.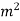 /sec.
/sec.
3] Impulsive Force :-
A very large force acting on a partical during short time interval.
4] Impulsive Torque:-
A large torque acting on a partical during short time interval.
5] Linear Impulse :- (vector quantity)
It is impulsive force acting on partical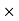 time.
time.
If large force (f) is acting on body short time interval between t1&t2 then

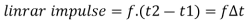
SI unit = N.sec
|
6] Angular impulse
It is large torque acting on a body 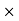 time duration.
time duration.
Angular impulse = 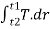
= T (t2-t1)
= T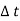 where
where
T= Torque
 = time duration.
= time duration.
SI unit :N.m.sec.
7] Impulsive motion :-
The resulting motion induced due to or created due to Impulsive force or torque is called as impulsive motion.
Impulse – momentum theorem :-
It states that “ when an unbalanced system of force is acting on the partical for short time interval , the impulse produced by all impulsive force is equal to change in momentum of partical.
From 2nd law of motion we have
F=m.a.
F= m.
F.dt = m.dv
Integration both side between the position 1& 2 ,

If force and mass are constant .
f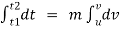
F(t)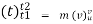
F [ -
- 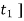 = m.[v- u ]
= m.[v- u ]
F 
But 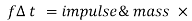 velocity = momentum
velocity = momentum
Impulse 1-2 = m1 –m2
Impulse = Final momentum - Initial momentum .
Impulse = change in momentum .
Where
Impulse = 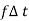 = f
= f 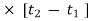
Final momentum = mv = m1
Initial momentum = mu = m2
Impulse in x direction = m ( V x – U x )
Impulse in y direction = m (V y – U y )
Impulse in z direction = m ( V z – U z )
Non – Impulsive force :-
Any force which does not produces any kind of impulse , is called as non-impulsive force .
Ex. 1] force exerted by spring
2] force of acting reaction .
3] internal forces. Etc.
Conservation of momentum – principal :-
we have impulse momentum theorem,
Impulse = final momentum – initial momentum.
But
When , 1] resultant of force is zero.
2] time interval 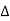 t is very very small,
t is very very small,
3] all external forces are non-impulsive ,
Then
Impulse = 0.
Impulse momentum theorem can be written as,
0 = final momentum – initial momentum .
Final momentum =initial momentum .
 =
= 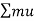 .
.
The total momentum remain constant .
i.e. Total momentum of partical is conservation.
Total momentum is conserved only in one direction.
Impact :-
It is the collision between two bodies , which occurs for a very small time interval . during this small time interval both bodies will exert large amount on each other .
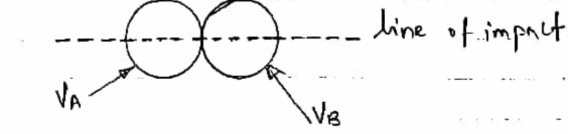
1] line of impact :-
It is the common normal to plane of contact .or It is the common normal to the surface of two bodies in contact during impact.
It is perpendicular to common tangent .
|
2] Direct impact :-
When the velocity of two bodies are along the line of impact then imput is said to be direct impact .bothpartical are moving along the line of impact .
|
3] Oblique impact :-
When both partical does not move along the line of impact , i.e. when velocities are not along the line of impact then it is called as oblique impact.
|
4] Central Impact :-
When mass centers of two colliding bodies lie on the line of impact , the impact is called as central impact.
|
5] Non central impact :-
When mass centers (c.g.) of the two colliding bodies do not lie on the line of impact , it is known to be non-central impact .
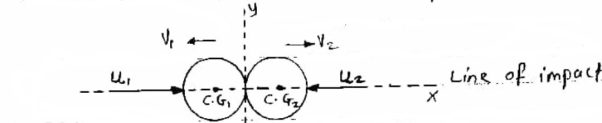
6] direct central impact :-
When the velocities of the two colliding bodies and their mass center lies on the line of impact , then it is called as direct central impact .
|
7] Oblique central impact
When the mass centers (C.G) of the two colliding bodies lies on the same line of impact but their velocities do not lie on the line of impact , then the impact is called as oblique central impact .
|
As par the law of conservation ,
Component of total momentum of two bodies along the line of impact is given by –
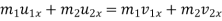
Component of momentum along the common tangent is

Restitution (Restoration)
After this impact , both objects tends to regain their original shape and size . this process is known as restitution or restoration . this process is known as restitution or restoration . this process contunes for small time duration which is called as period restitution .
Coefficient of Restitution (e)
It is the ratio of impulsses during the restoration period and deformation period .it is denote by e.
This is always positive and lies between o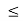 e
e 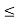 1.
1.
e = 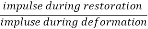
when the impact takes place , the two object initially goes under the deformation for small duration & then , they tries to region their original shape , size
1] perfectly elastic impact :-
In this impact , both bodies regain their shapes & size completely
i.e. there is complete restoration . here ,
a] momentum is conserved along the line of impact
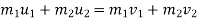
b] K.E. is also conserved .no loss of K.E. during impact
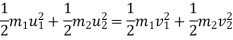
c] coefficient of restitution (e) = 1
e= 1= 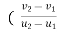 )
)
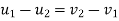
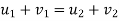
d] both bodies separates after input .
2] perfectly plastic impact :-
in this impact , both bodies are couple together after the impact and they move together with same velocity , here permanent deformation take place . so there is no restitution.
a] Here , momentum is conserved :-
Where V = common velocity of both bodies after Impact. b] K.E.is not conserved .there is loss of k.e. during impact . loss of K.E. = total k.e. before impact – total k. e. after impact loss of K.E. =
c] both bodied move together after impact. d] coefficient of restitution ( e ) = 0 .
|
3] partially elastic ( semi elastic ) impact .
In this impact , both bodies do not regain their original shape & size completely . but there is a partial restoration.
a] here momentum is conserved.
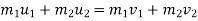
b] K.E. is not conserved .there is some loss in K.E
initial K.E. > KE after impact .
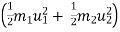 >
>
c] coefficient of restitution is more than zero & less than 1
0 < e < 1.
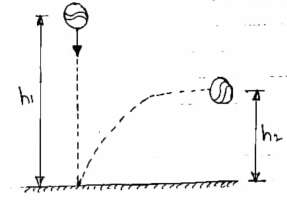
4] impact with very large mass ( infinite mass)
When a body of small collide with a body of very large mass as compared to first body, then the impact is considered as impact with infinite mass.
Ex .a ball is dropped on the floor .
|
a] in this type of impact , low of conservation of momentum cannot be applied .
b] there is no loss I KE due to impact
c] coefficient of restitution is
e = 
but velocity if floor before & after impact is zero.
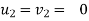
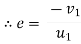
Velocity of ball just before the impact when it is dropped from height h1 is ,

After the impact ball rises to the height h2 , then its velocity after the impact is 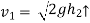
e 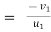 =
= =
= 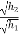
where ,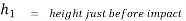

Two masses of 15 kg & 20 kg are moving along a straight line towards each other at velocities of 4 m/a & 2 m/s respectively . if e = 0.6, find the velocities of the masses immediately after the collision . also find %in K.E. due to impact .
|
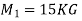
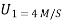
Let V1 &V2 are the velocities after collision , assume that both are towards right ( Using law of conservation of momentum,
(15 20 = 15V1+20V2 ___________1 Using coefficient of restitution e = 0.6 = V2-V1= 0.6 V 2 – V 1 = 3.6 -V 1 + V2= 3.6 ______________2 Solving 1 & 2 15 V1 + 20 V2 = 20 -V1 + V2 = 3.6 We get V2= 2.11 m/s ( & V1 = - 1.43 m/s ( Loss in KE = initiak KE- final KE loss of K.E. = = ( ½ =(120+40) – (16.65+44.52 ) = 160 - 60.97 Loss in K.E = 99.029 joule. % Loss in K.E. = 99.029/160 = 61.89%
|
The perfectly elastic balls 1 , 2 , 3 of masses 2kg 6kg 12kg respectively move along a line in same direction with velocities 12 m/s 4m/s and 2 m/s respectively. If the ball 1 strike the ball 2 which in horn strike ball 3 determine velocity of each ball after impact.
|
Given data
Ball 1
M1 = 2kg u1 = 12 m/s
Ball = 2
M2 = 6kg u = 4 m/s
Ball = 3
M3 = 12 kg u = 2 m/s
Consider the impact between ball 1 and ball2
For law of conversation of momentum
M1u1 + m2u2 = m1 v1 + m2v2
2*12 + 6*4 = 2v1 +6v2
48= 2v1 +6v2
2v1 + 6v2 = 48 - - - - - - - - - -- - - -- -eqn 1
As the balls are perfectly elastic
E=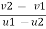 = 1
= 1
V2 – v1 = u2 – u1 = 12 -4 = 8
V2 – v1 = 8 - - - - - - - - - - - - - - - - - -eqn 2
Solving eqn 1 and 2
V1 = 0 and v2 = 8 m/s
As the ball strike each other ball 1 comes to rest and ball 2 moves forward ball s with new velocity of 8 m/s
U2 = 8 m/s
B) consider the impact between the ball 2 and 3
M2 u2 + m3 u3 = m2v2 + m3v3
6* 8 + 12*2 = 6V2 + 12v3
6V2 + 12 v3 = 72 ---------------- eqn 3
Are perfectly elastic balls
e = 1 =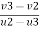 =
= 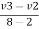
-V2 + v3 = 6 ------------------------ eqn 4
Solving eqn 3 and 4 we get
V2 = 0 and v3 =6 m/s
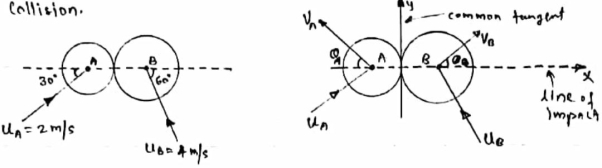
Two smooth balls A & B having mass of 4 kg and 8 kg respectively collider with initial velocities as shown in figure .if coefficient of restitution is e = 0.8 , find the velocities of each ball after the collision.
|
Ball – A
Using law of conservation of momentum along
( 4 6.928 + (-16) = - - Coefficient of restitution , e = 0.8 0.8 = VB X + VA X / VB X + VA X= 2.986 ---------------------2 Solving 1 & 2 we get VB X = 0.239 m/s VA X= 2.746 m/s Similarly , now component of velocity before and after the impact is conserved i.e. remain constant along the common tangent V AY = UAY = V BY= U B Y =4
|
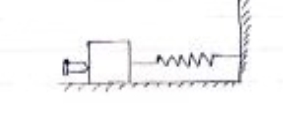
A 20 gm bullet horizontally into 300 block , which rest on smooth surface . after impact the bullet percentage into black the block moves to the right through 300 mm before momentarily coming to rest . determine speed of bullet as it strike the block the block is resting on smooth surface against the spring which is originally Unstretched& has a constant of 200 n/m
|
Given data
For bullet
M1 =0.02kg, u= ?
for block ,
m2 = 0.3 kg , u2 = 0
as the bullet penetrates into the block after the impact
the impact is perfectly plastic .
after impact velocity of block & bullet will be equal ,
V = V2 = V1 = comment velocity
By Appling law of conservation of momentum , for impact
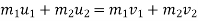
0.02 u 1 +0.3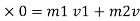
0.02 u 1 = ( m1 + m2 )v
0.02 u 1 = (0.02 + 0.3) v
0.02U 1 = 0.32 v
As the impact takes place , the black along with bullet will move toward right against spring force before coming to rest here spring will be compressed by 300 mm
Applying work energy principal just after the impact ,
Total w.d= ke2 – ke 1
w.d. by spring force = KE 2 – KE 1
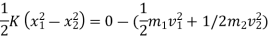
½ 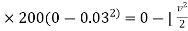 (0.02+0.3) ]
(0.02+0.3) ]
-9 = - 0.16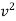
V = 7.5 m/s - ------ put this is in equation 1
0.02 u 1 = 0.32 v1 = 0.32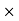 7.5
7.5
U 1 = 120 m/s - - - - -speed of the bullet as it strikes the block
A 100 gm ball dropped from a height of 600 mm on a small plate .it rebounds to a height of 400 mm when plate is directly resting on ground floor and it rebounded to a height of 250 mm when foam rubber matt is placed between plate and ground determine the coefficient of restitution between the plate and ground .
Case 1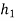 = 600 mm
= 600 mm
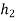 = 400 mm
= 400 mm
e =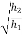
e = 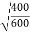
e = 0.816
case 2
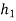 = 600 mm
= 600 mm
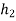 = 250 mm
= 250 mm
e = 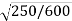
e = 0.645.
Reference Books:
1. Engineering Mechanics by S. P. Timoshenko and D. H. Young, McGraw- Hill publication
2. Engineering Mechanics by J. L. Meriam and Craige, John Willey
3. Engineering Mechanics by F L Singer, Harper and Rowe publication
4. Engineering Mechanics by A. P. Boresi and R. J. Schmidt, Brooks/Cole Publication