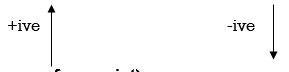Unit-1
Resolution and Composition of Forces
Fundamental Concepts
1. Particle
It is a material point which contains definite quantity of matterwithout dimension.
2. Rigid Body
It is a body which does not undergo any deformation (change in shape and size) under the action of external force.
Combination of large no of particles which remains at fixed distance from each other when external force is applied or removed.
3. Force
An action which tends to change the state of rest of body or motion of body on which it acts.
1. Newton’s 1stLaw:-
Everybody continues to be in its state of rest or in the state of uniform motion along straight line unless it is acted upon by external unbalanced force.
2. Newton’s 2ndLaw:-
When unbalanced force acts on particle, it will have an acceleration which is proportional to the magnitude of force. This acceleration will be in the direction of force along straight line.
Rate of change of momentum of body is directly proportional to the force acting on it & it is in the direction of force.
3. Newton’s 3rdLaw:-
Forces of action & reaction between bodies in contact will have same magnitude, line of action but opposite direction.
Mechanics:-
The branch of physical science that deals with state of the rest of the motion is called as mechanics.
Engineering. Mechanics:-
The branch of applied science, which deals with laws & Principals of Mechanics along with their applications to the real life engineering problem.
Engineering Mechanics is essential for an engineer in
- Planning, designing & construction of various structures & machines.
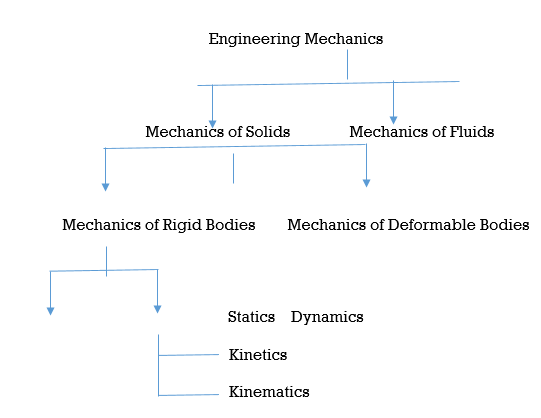
Classification of Engineering Mechanics:-
|
In our syllabus, we are going to study the mechanics of Rigid Bodies i.e. Statics & Dynamics.
Statics:-
It is the branch of Engineering Mechanics which deals with the forces and their effects ( acting ) upon the bodies which are at rest.
Dynamics:-
It is the branch of engineering Mechanics which deals with forces & their effects (acting) upon the bodies which are in motion.
Dynamics is again divided into two categories:
1>. Kinetics
2>. Kinematics
Kinetics:-
It is the branch of Dynamics which deals with the bodies in motion by considering the forces which cause the motion.
Kinematics:-
It is the branch of Dynamics which deals with the bodies in motion without considering the force which is responsible for the motion.
Mass ( m ) :-
The quantity of matter possessed by a body,
S.I. unit: - gram (g)
Kilogram (kg)
1 kg = 1000 g
Weight (W):-
Force acting on the object due to gravity.
It is the product of mass & gravitational Acceleration.
W = m x g
S.I. Unit: - Newton (N)
Kilo Newton (KN)
1 KN = 1000 N.
Force [(F) or ( P )] :-
It is an external agency which produces or tends to produce, destroy or tends to destroy motion.
OR
It is an external agent which changes or tends to change the state of motion of body.
It is a vector quantity.
Force is also known as rate of change of momentum.
As momentum = mass x velocity
But mass will never change, then
Force = mass x rate of change of velocity
= mass x Acceleration
F = P = ma
S.I. Unit: - Newton (N)
KiloNewton (KN) = 103 N
MegaNewton (MN) = 106 N
GigaNewton (GN) = 103 N
TeraNewton (TN) = 1012 N
1 Kg Force:-
Force required to produce unit gravitational acceleration on unit mass.
01 kg force = mass x Accln(gravity)
= 1 kg x 9.81 m / s2
= 9.81 kg.m / s2
1 kg.F = 9.81 Kg m / s2
1 kg.F = 9.81 N
i.e. 1 Kg = 9.81 N
Characteristics of Force:-
1. Magnitude:- The value of force i.e. 10N, 2KN, etc.
2. Direction:- Line of action & angle formed with fixed axis.
3. Nature of force or sense:-It means whether the force is push or pull.
|
Push:- Force acting towards the point
Pull: - Force acting away from the point.
4. Point of application:-
The point at which or through which the force acts.
Effects of Force:-
Force may produce following effects on the body.
1. It may change the state of body.
i.e. if body is at rest, force may bring it in motion or if body is in motion, force may accelerate it or force may stop it or may retard it.
2. It may produce internal stress in the body.
3. It may produce deformation in non-rigid body.
4. It may produce rotational effect in body.
5. It may keep the body in stable state (Equilibrium).
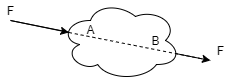
Principle of Transmissibility of force: -
The state of the rigid body will not change if force acting on a body is replaced by another force of same magnitude & direction acting anywhere on the body along the line of action of replaced force.
|
The value of force will not change along the
Line of action of force within the body.
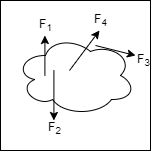
System of Force:-
When a single agency is acting on body then it is known as force. But when no of forces are acting on the body simultaneously, then it is known “System of force”.
Types of Force System:-
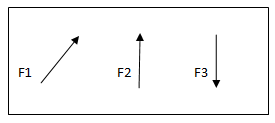
1. Co-planer Forces
2. Non Co-planer Forces
3. Co-linear Forces
4. Non Co-linear Forces
5. Concurrent Forces
6. Non Concurrent Forces
7. Parallel Forces (Like&unlike)
8. Coplanar Concurrent Forces
9. Coplanar Non Concurrent Forces
10. Non Coplanar Concurrent Forces
11. Non Coplanar Non Concurrent Forces
1. Co – planer Force System / Forces:-
The forces whose line of action lie on the same plane are called as Co-planer Forces.
|
The forces which are acting in the same plane are known as co-planer forces.
2. Non Co-planer Force System / Forces:-
- A forces whose line of action does not lie in the same plane ( i.e. lie in different planes )
- Forces which are acting in the different planes known as non-co-planer forces (system).
|
3. Co-linear force system / Forces:-
- The forces whose line of action lies on the same line are called as co-linear forces.
- The forces which are acting along the same straight line are called as co-linear forces.
4. Non – Collinear Forces / force system:-
- The forces which are not acting along the same straight line are known as non-co-linear forces.
- The forces whose line of action doesn’t lie on the same line.
|
5. Concurrent forces / Force system:-
- The forces whose line of action meets at one common point are called concurrent forces.
- The forces which are passing through a common point are concurrent forces.
- The forces which meets at one point are concurrent forces.
6. Non Concurrent force system / forces:-
- The forces which are not passing through common point OR
- The forces whose line of action does not meet at common point OR
- The forces which does not meet at one point are called as non-concurrent forces.
|
7. Parallel Forces / Force system:-
The forces whose line of actions are parallel to each other are called as parallel forces.
a) Like parallel Forces :-
The forces whose line of actions are parallel to each other and having same direction are called like parallel forces.
Forces which are parallel to each other & acting in same direction are called as Likeparallel forces.
|
b) Unlike parallel Forces:-
The forces which are parallel to each other but having different directions or
The forces which are parallel to each other & acting in opposite direction are called as unlike parallel forces.
|
8. Coplanar concurrent forces:-
The forces which meets at one point & their lines of action also lie on the same plane are called as coplanar concurrent force system.
|
9. Coplanarnonconcurrent forces:-
The forces which do not meet at one point but their line of action lies on the same plane are known as coplanar non-concurrent system of force.
|
10. Non Coplanar concurrent forces:-
The forces which meets at one point but their line of action do not lie on the same plane are known as non-coplanar concurrent forces.
|
11. Non coplanar non concurrent forces:-
Their forces which do not meet at one point & their lines of actions do not lie on the same plane are called as non - coplanar non concurrent forces.
|
Resultant Force:-
- If number of forces are acting simultaneously on a body, then it is possible to find out single force which could replace them, i.e. which would produce the same effect as produced by all given forces. This single force is called as Resultant force.
OR
- It is a single force which produces the same effect that is produced by number of forces when acting together.
Resultant is denoted by (R)
Equilibrant:-
It is the single force which when acting with all other forces keeps the body at rest or in equilibrium.
It is denoted by (E).
|
Composition:-
The process of finding out the resultant force of a given force system.
Resolution:-
It is the procedure of splitting up a single force into number of components without changing the effect of same on the body.
Forces are generally resolved into two components along two mutually perpendicular directions.
|
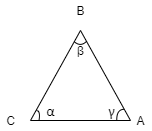
Law of parallelogram of forces:-
If two forces acting simultaneously on a particle, be represented in magnitude & direction by two adjacent sides of parallelogram, then the diagonal passing through the point of intersection of two forces will represent the resultant in magnitude & direction.
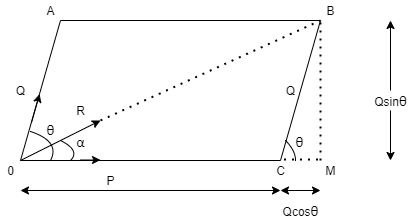
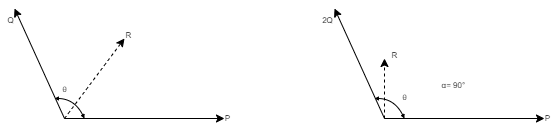
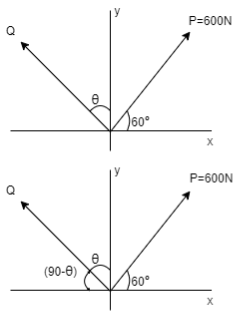
Consider two forces P & Q acting at a point represented by two sides OA & OC of parallelogram OABC.
Let, θ is the angle between two forces P & Q. α be the angle between Force P & Resultant R.
Let’s draw a line BM perpendicular to OC which intersects OC at M. In Δ CMB Sin θ = BM / BC = BM / Q BM = Q Sin θ Also, Cos θ = CM / BC = CM / Q CM = Q Cos θ Now in Δ OMB, We have, (OB) 2 = (OM) 2 + (BM)2 R2 = (OC + CM) 2 + (BM)2 R2 = (P + Q Cos θ) 2 + (Q Sin θ)2 = P2 + 2PQ Cos θ + Q2 Cos2 θ+ Q2 Sin2 θ = P2 + 2PQ Cos θ + Q2(Cos2 θ+ Q2 Sin2 θ) = P2 + 2PQ Cos θ + Q2 Taking sq. root,
R = √P2 + Q2 + 2PQ Cos θ . . . . Magnitude
Tanα = Q Sin θ / P + Q Cos θ . . . . Direction
|
Examples based on Parallelogram Law of forces:-
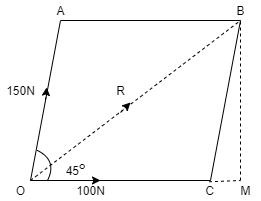
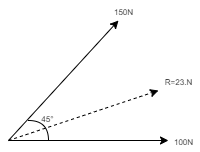
1. Two forces of 100 N & 150 N are acting simultaneously at a point. What is the resultant of these two forces, if the angle between them is 450.
Given: P = 100 N Q = 150 N θ = 45o R = ?α= ?
Solution: Accr to law of parallelogram of force, R = √ P2 + Q2 + 2PQ Cos θ R = √ 1002 + 1502 + 2 x 100 x 150 x Cos 450 R = 231.76 N R ≈ 232 N - - - Ans - - - magnitude
tanα = Q Sin θ / P + Q Cos θ = 150 Sin 450 / 100 + 150 Cos 450 = 106.066 / 206.066 α = 27.290. . . . . Direction
Ans:
2. The sum of two forces is 270 N & their resultant is 180 N. If Resultant is Perpendicular to P, find the two forces P & Q. Given:
P + Q = 270 N R = 180 N α = 900 Soln :Accr to law of parallelogram, Tanα = Q Sin θ / P + Q Cos θ Tan 90 = Q Sin θ / P + Q Cos θ
∞ = Q Sin θ / P + Q Cos θ
Here if P + Q Cos θ = 0, then only above term will become infinity. Thus, P + Q Cosθ= 0 P = - Q Cos θ -P = Q Cosθ . . . . (1) Now, R2 = P2 + Q2 + 2PQ Cos θ 1802 = P2 + Q2 + 2P(-P) . . . from eqn (1) 1802 = P2 + Q2 + (-2P2) 1802 = P2 -2P2 + Q2 1802 = - P2 + Q2 1802 = Q2 - P2 1802 = (Q- P) (Q+ P) = (Q- P) x 270 Q- P = 1802 / 270 Q- P = 120 . . . (ii) & we know that Q + P = 270 . . . (iii) Solving (ii) & (iii) i.e. add eqn (ii) & (iii) Q – P = 120 + Q + P = 270 _______________ 2Q + 0 = 390
2Q = 390 Q = 195 N &P = 75 N . . . Ans
3. For two forces P & Q acting at a point. Maximum resultant is 2000 N and minimum magnitude of resultant is 800 N. Find values of P & Q.
Sol: We know that, R2 = P2 + Q2 + 2PQ Cos θ For max value of R, Cos θ must be 1 i.e. Cos θ = 1 i.e. θ = 0, then only cosθ = 1 Rmax = √ P2 + Q2 + 2PQ Cos θ = √ P2 + Q2 + 2PQ Cos 0 = √ P2 + Q2 + 2PQ 2000 = √ P2 + 2PQ + Q2 = √ (P + Q)2 2000 = P + Q . . . .Eqn (1)
Now for minimum value of R, θ = 1800 Rmin= √ P2 + Q2 + 2PQ Cos θ = √ P2 + Q2 + 2PQ Cos θ = √ P2 + Q2 - 2PQ = √ P2 - 2PQ+ Q2 = √ (P – Q)2 800 = P – Q . . . . . eqn (ii) Solving eqn (i) &eqn (ii) we get, i.e. Add eqn (i) & (ii), P + Q = 2000 - P - Q = 800 _______________ 2P + 0 = 2800 P = 2800 / 2 P = 1400 N ….Ans
&P + Q = 2000 1400 + Q = 2000 Q = 600 N . . . Ans
Ans P = 1400 N Q = 600 N
4. The angle betn the two forces P & Q is θ. If Q is doubled then new resultant is perpendicular to P. Prove that Q = R.
R2 = P2 + Q2 + 2PQ Cos θ . . . (1) Also tan 90 = Q Sin θ / P + Q Cos θ ∞ = 2Q Sin θ / P + (2Q) Cos θ= Q If P + (2Q) Cos θ = 0 then only above term will be infinity. P + (2Q) Cos θ = 0 -P = (2Q) Cos θ-- put in eqn (I) R2 = P2 + Q2 + (P x (-P)) = P2 + Q2 - P2 R2 = P2 Taking sq. root R = P -- -Proved
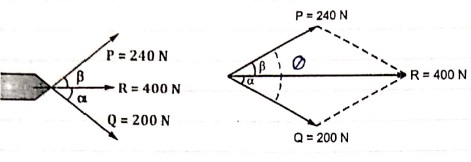
5. The angle betn the two concurrent forces is 900 & their resultant is 2500 N. The resultant makes an angle of 460 with one force. Determine magnitude of each force. PU – many 14 – 4m
By using, R2 = P2 + Q2 + 2PQ Cos θ 25002 = P2 + Q2 + 2PQ Cos 90 As cos 90 = 0 then 25002 = P2 + Q2 . . . (1) Now, Tanα = Q Sin θ / P + Q Cos θ = Q Sin 90 / P + Q Cos 90 Tanα = Q / P Tan46 = Q / P Q = 1.0355 P - - substitute in eqn (1) 25002 = P2 + [(1.0355)2 P2] P2 = 3017537.93
P = 1737 N Q = 1798 N
Let Q = (α + β ) Using law of parallelogram, R2 = P2 + Q2 + 2PQ Cos θ 4002 = 2400 + 2002 + 2 x 240 x 200 Cos θ 62400 = 96000 Cos θ Cos θ = 62400 / 96000 = 0.65 θ = Cos-1 (0.65) = 49.460 θ = 49.460
We know that Tanβ = Q Sin θ / P + Q Cos θ Tanβ = 200 Sin θ / 240 + (200 Cos θ) = 200 Sin 49.46 / 240 + (200 Cos 49.46) = 0.411 β = tan-1 (0.411) β = 22.330 -- Direction of P
Q = α + β 49.46 = α + 22.33 α = 27.130 -- Direction of Q
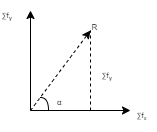
Resultant of more than two Forces:- Method of Resolution When two or more coplanar concurrent or non-concurrent forces are acting on a body, then the resultant can be found out by using resolution of forces. A resolution procedure is described below. 1. Resolve all the forces horizontally & find the algebraic sum of all the horizontal components. If a force is denoted by F, then Fx= Horizontal component of Force F (along x dirn). Fy= Vertical component of Force F (along y dirn). Thus, in this step find ∑Fx
2. Resolve all the forces vertically & find the algebraic sum of all vertical components. i.e. find ∑Fy.
3. The resultant R of the given Forces will be given by the equation: R = √(∑ Fx) 2 + (∑Fy)2
4. The resultant force will be inclined at an angle θwith horizontal, such that tanα = ∑Fy /∑ Fx
Resolution of Force:- Following 3 methods are used to resolve the force. 1. Orthogonal Resolution (Perpendicular resolution) 2. Non – perpendicular / Non – Orthogonal resolution 3. Resolution into two parallel components.
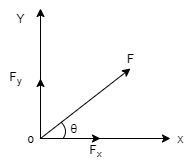
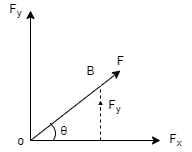
1. Orthogonal or Perpendicular Resolution:- In this method, single force is split up into two components which are perpendicular to each other along x direction & y direction. Consider Force F as shown below, which makes an angle (1) with x-axis.
Then, Fx = Horizontal component of force F along x dirn Fy = Vertical component of force F along y dirn. θ = angle made by force F with x-axis. & angle betn X & Y axis is 900 Now, lets draw a perpendicular to X axis at point A. This perpendicular will intersect F at point B as shown below.
In right angle Δ OAB, Sin θ = AB / OB = Fy / F & Cos θ = OA / OB Sin θ = Fy / F Cos θ = Fx / F Fy = F Sin θ Fx = F Cos θ ……y component of force ……x component of force
Following are the different cases of resolution of Force into two perpendicular components.
Sign Conventions: 1. Component acting towards right are positive & towards left are considered as negative.
2. Component acting upward are positive & acting downward are considered as negative.
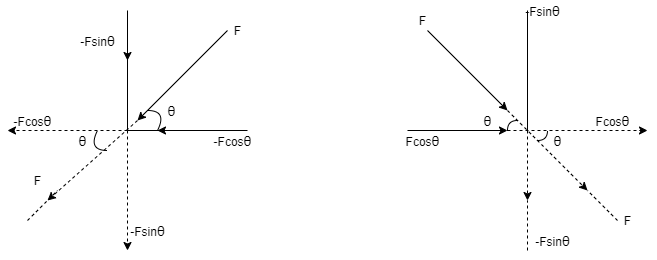
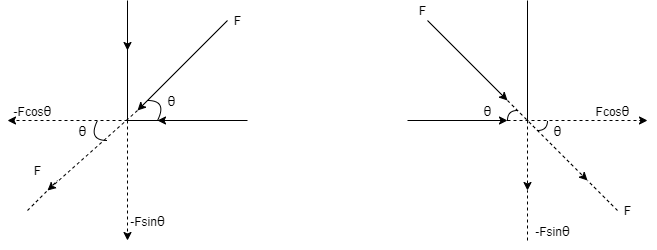
Cases of Resolution (force acting towards the point ) :- ( a ) Force in 1st quadrant ( b ) Force in 2nd quadrant
Fx = - F Cos θ Fx = F Cos θ Fy = - F Sin θ Fy = - F Sin θ
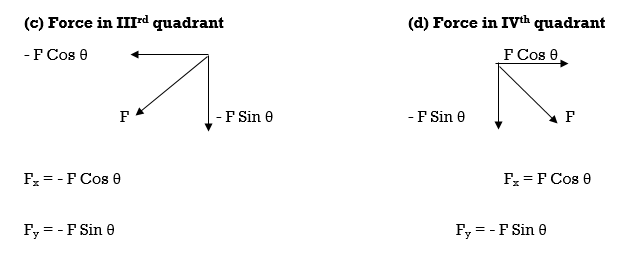
(c) Force in 3rd quadrant ( d ) Force in 4th quadrant
Fx = F Cos θ Fx = - F Cos θ Fy = F Sin θ Fy = F Sin θ
Another method of Resolution of force acting towards the point in different quadrants.
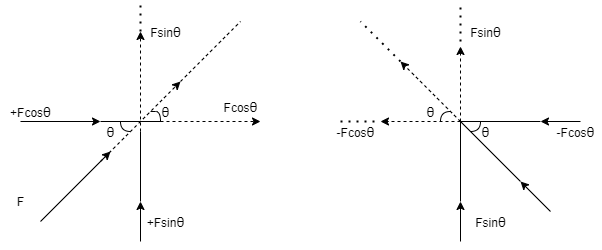
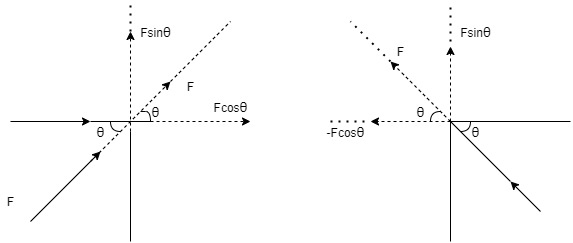
( a ) Force acting towards the pointing 1st quadrant( b ) Force acting towards point in the 2nd quadrant
Fx = - F Cos θ Fx = F Cos θ Fy = - F Sin θ Fy = - F Sin θ
(c) Force acting towards the point ( d ) Force acting towards the point in3rd quadrant in the 4th quadrant
Fx = F Cos θ Fx = - F Cos θ Fy = F Sin θ Fy = F Sin θ
Special Cases of Resolution:-
Component along the plane = W Sin θ Component perpendicular to plane = W Cos θ
2.
Examples based on orthogonal Resolution (Perpendicular components). 1. A force of 900 N acts from origin to a point A (1, 2, and 5). Find two orthogonal components.
The angle of force with horizontal is, Tanθ = 5 / 12 θ = tan-1(5 / 12) force is in 1st quadrant
θ = 22.620
x-Component of force, Fx = F Cos θ = 900 Cos 22.62 Fx = 830.77 N
Y component of force, Fy = F Sin θ = 900 Sin 22.62 Fy = 346.16 N
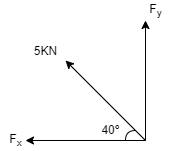
2. Find x & y components for the following force systems. (a)
Here force is in 2nd quadrant X component, Fx = - F Cos θ = - 5 Cos 40 = -3.83 KN = 3.83 KN (left) Y component, Fy = F Sin θ = 5 Sin 40 = 3.21 KN upwards
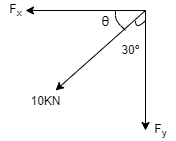
θ= angle of force with X axis = 90 – 30 θ = 600 Here force is in 3rd quadrant X component, Fx = - F Cos θ = - 10 cos 60 = - 5 KN Fx = 5 KN towards left Y component, Fy = - F Sin θ Fy = - 10 Sin 60 = - 8.66 KN Fy = 8.66 KN Downward
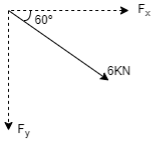
( c )
Here, force is in 4th quadrant &θ = 600 X component, Y component, Fx = F Cos θ Fy = - F Sin θ = 6 Cos 60 = - 6 Sin 60 = -5.2 KN Fx = 3 KN towards right Fy = 5.2 KN. Downward
( d )
** Convert push type force into pull. Thus force is in 2nd quadrant & Q = 700 **
X component, Fx = - F Cos θ = - 4 Cos 700 Fx= -1.37 KN towards left Y component, Fy = F Sin θ = 4 Sin 700 Fy = 3.76 KN upward
( e )
Here, θ = 550, force is in 2nd quadrant X component, Fx = - F Cos θ = - 100 Cos 550 Fx = - 57.36 N towards left
Y component, Fy = F Sin θ = 100 Sin 550 Fy = 81.91 N upward
( f )
Here force is in 4th quadrant, θ = 500, X component, Fx = F Cos θ = 15 Cos 500 Fx = 9.64 N towards right Y component, Fy = - F Sin θ
= - 15 Sin 500 Fy = 11.49 N Downwards
3. Find x & y components for the following force system ( a )
Here force is on negative X axis. θ = 00, X component, Fx = -F Cos θ = -P Cos 0 = - P Fx = P towards left
Y component, Fy = F Sin θ = P Sin 0 Fy = 0
( b )
Here force is on Y axis. θ = 900, X component, Fx = -F Cos θ = -P Cos 90 = 0 Fx = 0
Y component, Fy = F Sin θ = P Sin 90 = P Fy = P
Thus we can say that, If a force is an X axis, then its X component is the force itself & Y component will be zero. If force is on Y axis, then its y component is the force itself & x component will be zero.
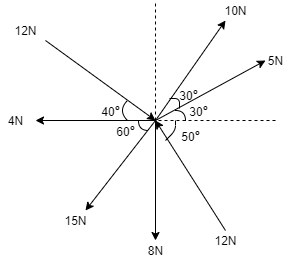
3. Determine the resultant of following force system as shown in figure.
Solution:
Convert all the push type forces into pull type. Now resolving all the forces horizontally along x axis, We have ∑ Fx = 5 Cos 300 + 10 Cos 600 – 12 Cos 500 – 4 – 15 Cos 600 + 12 Cos 400 ∑ Fx= 0.69 N towards left (due to –ve sign)
Now resolving all the forces vertically along Y axis, We have ∑Fy = 5 Sin 300 + 10 Sin 600 + 12 Sin 500 – 15 Sin 600 – 8 – 12 Sin 400 ∑Fy = - 8.35 N ∑Fy = 8.35 N Downwards The resultant is given by, R = √(∑ Fx) 2 + (∑Fy)2 R = √(0.69) 2 + (8.35)2 R = 8.38 N -- magnitude of Resultant
Direction of Resultant is given by, tanα = ∑Fy / ∑ Fx = 8.35 / 0.69 = 12.1014 α= tan-1( 12.1014 ) α= 85.280
As ∑ Fx& ∑Fy are negative, thus, Resultant lie in 3rd quadrant.
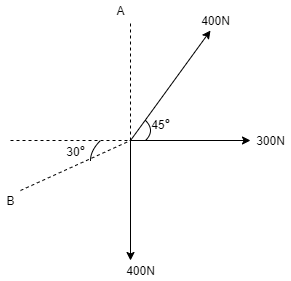
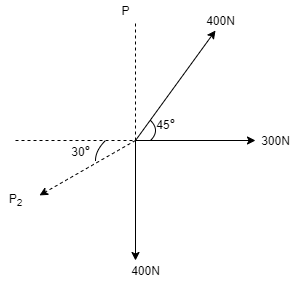
4. Three concurrent co-planer forces acts on a body at point 0. Determine two additional forces along OA & OB such that Resultant of five forces is zero. Refer the given figure.
Solution:
Let force along OA = P1 & Force along OB = P2 As it is given that Resultant R = 0, thus ∑ Fx = 0 ∑Fy = 0 Now let us resolve the forces horizontally, Using ∑Fx = 0 300 + 400 Cos 45 – P2 Cos 30 = 0 300 + 282.843 – 0.866 P2 = 0 0.866 P2 = 582.843 P2 = 673.03 N
Resolving forces vertically, using ∑Fy = 0, 400 Sin 45 + P1 – P2 Sin 30 – 400 = 0 282.843 + P1 – 673.03 Sin 30 – 400 = 0 -453.672 + P1 = 0 P1 = 453.672 N --- Ans Ans P1 = 453.672 N & P2 = 673.03 N
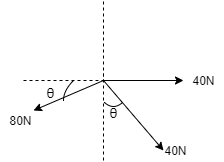
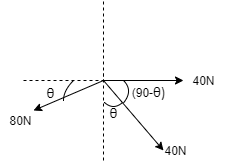
5. Determine the angle θ for which the resultant of the three forces is vertical. Also find corresponding magnitude of Resultant by referring the fig given below.
Solution:-
The Resultant R is vertical, but direction is unknown. Assuming R to be downwards, ∑ Fx = 0 --- because R is vertical ∑Fy = - R Resolving forces horizontally ∑ Fx = 0 40 – 80 Cos θ + 40 Cos (90 - θ) = 0 40 – 80 Cos θ + 40 Sin θ = 0 Divide both sides by 40 1 - 2 Cos θ + Sinθ = 0 1 + Sinθ = 2 Cos θ Squaring both sides, (1 + Sinθ)2 = (2 Cos θ)2 1 + 2Sinθ+ Sin2θ = 4 Cos2θ 1 + 2Sinθ+ Sin2θ = 4(1 - Sin2θ) 1 + 2Sinθ+ Sin2θ = 4 -4 Sin2θ 5 Sin2θ + 2Sinθ – 3 = 0 Solving the eqn Sinθ= 0.6 OR Sinθ = -1 θ= Sin-10.6 ORθ = Sin-1(-1) θ= 36.870OR θ = - 900 ---neglecting this θ= 36.870
Now resolving forces vertically ∑Fy = - R -80 Sin θ – 40 Sin (90 - θ) = - R -80 Sin 36.87 – 40 Sin (90 – 36.87) = - R -R = -80.00 N R = 80 N
As the answer is positive, our assumption of R being downward is correct.
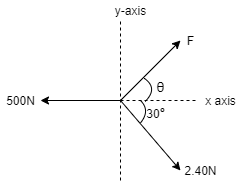
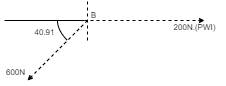
The force system as shown in figure have a resultant of 200 N along positive Y axis, determine the magnitude & direction (θ) of Force F.
As resultant of 200 N lie on positive Y axis i.e. upwards, it means, ∑ Fx = 0 & ∑Fy = R
Now Resolving forces horizontally, ∑ Fx = F Cos θ – 500 + 240 Cos 30 = 0 F Cos θ= 500 - 240 Cos 30 F Cos θ= 292.154 … (i)
Resolving forces vertically, ∑Fy = R F Sin θ – 240 Sin 30 = 200 F Sin θ= 320 …. (ii) Now divide eqn (ii) by eqn (i) F Sin θ/ F Cos θ = 320 / 292.154 Tanθ= 1.0953 θ = tan-1 1.0953 θ = 47.60
From eqn (i) F Cos θ = 292.154 F Cos 47.6 = 292.154 F = 433.31
The resultant of two forces P & Q is 1200 N vertical. Determine force Q & corresponding angle θ for the system of force as shown in figure.
As Resultant is vertical (Assuming it be upward) ∑ Fx = - R & ∑Fy = 0
Now resolving forces horizontally, ∑ Fx = - R P Cos 60 - Q Cos(90 –θ) = -1200 600 Cos 60 - Q Sinθ = -1200 - Q Sinθ = -1200 – 300 Q Sinθ = 1500 …. (i)
Now resolving forces vertically, ∑Fy = 0 600 Sin 60 - Q Sin (90 - θ) = 0 Q Cos θ = 519.61 …. (ii) Divide eqn (i) by eqn (ii), we get Q Sin θ/ Q Cos θ = 1500 / 519.61 Tanθ = 2.886 θ = 70.890 . . . . Put in eq (i)
Q Sin θ = 1500 Q Sin 70.89 = 1500 Q = 1500 / Sin 70.89 Q = 1587.45 N
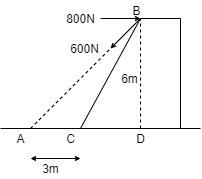
Combine two forces 800 N, which act on the fixed dam structure at B into a single equivalent force R, if AC = 3 m, BC = 6 m & angle BCD = 600. Refer fig.
Soln:-
In ΔBDC, Angle BDC = 900 Sin 60 = BD / BC = BD / 6 BD = 6 Sin 60 = 5.2 m
Similarly, Cos 60 = DC / BC = DC / 6 DC = 6 Cos 60 = 3 m
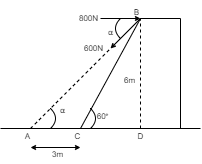
Now in ΔBDA, Angle BDA = 900 Tanα = BD / AD Tanα = BD / AC + DC = 5.2 / 3 + 3 = 5.2 / 6 Tanα = 0.866 α = 40.910
Thus force diagram will be as follows,
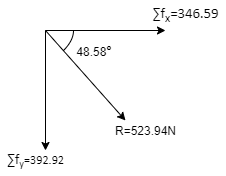
Now resolving forces acting at B in Horizontal diagn, We have, ∑ Fx = 800 - 600 Cos 40.91 ∑ Fx = 346.59 N… (Toward right)
Resolving forces vertically, ∑Fy = -600 Sin 40.91 = -392.92 N (Downward)
Resultant R is given by, R = √(∑ Fx) 2 + (∑Fy)2 = √(346.59) 2 + (392.92)2 R = 523.94 N
Direction of Resultant, Tanθ = ∑Fy / ∑ Fx = 392.92 / 346.59 Tanθ= 1.134 θ = 48.580
As ∑ Fx is positive & ∑Fyis negative, resultant will lie in 4th quadrant.
Ans:
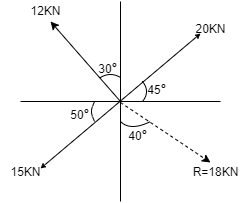
Q. R = 18 kN is the resultant of four concurrent forces out of which only three are known. Find the fourth forcein magnitude and direction.
Here Resultant is given in figure. R = 18 kN Angle of Resultant with x-axis = 90 – 40 = 500 We know that Rx = X component of Resultant = ∑ Fx= 18 Cos 50 Ry = Y component of Resultant = ∑ Fy= - 18 Sin 50 Assume that fourth force is F which makesθ angle with x-axis. X component of Force F will be, = F Cos θ Y component of Force F will be = F Sin θ Resolving forces along X & Y dirn, ∑ Fx = 20 Cos 45 – 12 Cos 60 – 15 Cos 50 + F Cos θ 18 Cos 50 = – 1.49 + F Cos θ
F Cos θ = 13.06 …… (1)
∑Fy = 20 Sin 45 + 12 Sin 60 - 15 Sin 50 + F Sin θ -18 Sin 50 = 13.04 + F Sin θ F Sin θ = - 26.83 …….. (2) From eqn (1)& (2) As X component of Force F is F Cos θ which is positive & Y component of Force F is F Sin θ which is negative It means Force F is in fourth quadrant. Divide eqn( 2 ) by eqn ( 1 ) FSin θ / F Cos θ = -26.83 / 13.06 Tanθ = (- 2.054) θ = tan-1 (-2.054) = - 64.040 θ = 64.040 . . . . Negative sign indicates 4th quadrant From eqn (1), F Cos 64.04 = 13.06 F = 29.83 N
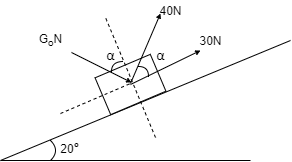
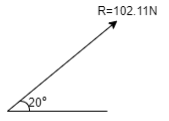
(Q) Determine the required value of α if the resultant of three forces is to be parallel to the inclined surface. Find the corresponding magnitude of the Resultant.
Let us select X axis parallel to the inclined plane. As resultant is acting parallel to the plane, let’s assume that it is acting along positive x dirn i.e. acting up the plane. As resultant is acting along +ve x axis, its y component will be zero. ∑ Fy = 0 ∑Fx = R 30 + 40 Cos α + 60 Sin α= R . . . . (1) Also, ∑ Fy = 0 40 Sin α - 60 Cos α = 0 40 Sin α = 60 Cos α Sin α / Cos α = 60 / 40 Tanα = 6 / 4 α = 56.30
R = 30 + 40 Cos α + 60 Sin α = 30 + 40 Cos 56.3 + 60 Sin 56.3 R = 102.11 N
(2) Non – Perpendicular / Non – Orthogonal Resolution:- When a force is resolved or split into two directions which are not perpendicular to each other, then the resolution is called as Non – perpendicular / Non – orthogonal.
Sine Rule
It states that the ratio of two sides of an oblique triangle is in same proportion as that of the ratio of sines of their opposite angle. OR The ratio of two sides of Δle will be equal to the ratio of sine of their opposite angle. AB / BC = Sin α / Sin ᵞ . . .(1) BC / AC = Sin ᵞ / Sin β . . . (2) AC / AB = Sin β / Sin α . . . (3) Thus we can write AB / Sin α = BC / Sin ᵞ = AC / Sin β ---- Sine rule Thus to resolve the force into two Non – perpendicular components, Construct the parallelogram by keeping original given force along diagonal & two components along two sides of parallelogram passing through point of application of force.
In Δ OAC, By Sine rule, FOB / Sin α = FOA /Sin β = F / Sin [180 – (α + β)] Using above equation, two components i.e. FOB& FOA can be calculated.
(Q) Resolve 200 N force into two components along A & B directions. Refer the given figure.
Solution:-
An angle betn OA & OB is 1000, resolution is non perpendicular. Thus in Δ OBC, by sine rule, 200 / Sin 80 = FOB / Sin 30 = FOA/ Sin 70 FOB = 200 / Sin 80 x Sin 30 FOB = 190.84 N
Similarly, 200 / Sin 80 = FOA / Sin 70 FOA = 200 Sin 70 / Sin 80 FOA= 101.5 N
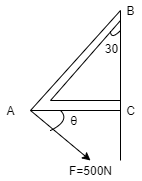
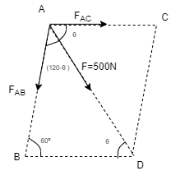
The force F acting on the frame has a magnitude of 500 N & it is to be resolved into two components acting along strut AB & AC. Determine the angle θ so that the component FAC is directed from A towards C & has magnitude of 400 N. Refer the given figure.
Solution :-
Because AC & AB are not perpendicular, let’s use non – perpendicular resolution. Thus in ΔADB1 ,by Sine rule, FAB/Sin θ = FAC / Sin (120 - θ) = F / Sin 60 As FAC = 400 N 400 /Sin (120 - θ) = 500 / Sin 60 400 Sin 60/ 500 = Sin (120 - θ) 0.963 = Sin (120 - θ) 120 – θ = 43.87 Θ = 76.130 . . . . Ans
|
Moment:-
The turning effect produced by a force on the body on which it acts is called as Moment.
Moment of force about any point is the product of magnitude of force and perpendicular distance of force from the point about which moment is to be taken.
|
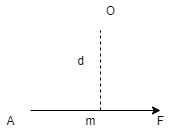
Let force F is applied at point A as shown & O is any point about which we want to take moment.
Thus from point O, draw OM line perpendicular to the line of action of force.
OM = d = Perpendicular distance betn Force & point O.
Moment = M = F xd
Graphical representation of Moment:-
- Select suitable scale to locate the force graphically.
- Draw a line parallel to line of action of force. Length of this line can be calculated from selected scale.
- Length of a line will be equal to magnitude of force.In the figure, Force F is represented by line AB.
- Now let O is the moment centre &
OM = d = perpendicular distance
By definition, Mo = F xd
Now join OA & OB, then
In Δ OAB
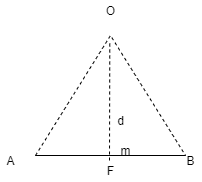
Area (ΔOAB) = ½ x AB x OM
2 (Area of ΔOAB) = F xd = Mo
Thus the moment of any force about any point is numerically equal to twice area of triangle in which base represents force & height represents the perpendicular distance.
It states that if number of forces are acting simultaneously on a body, the algebraic sum of moments of all the forces about any point is equal to moment of their resultant about same point.
Mathematically,
∑(F xd) = (R x X)
Where, F = All forces acting on a body
d = ḻlar distance
R = Resultant of all forces
X = ḻlar distance of Resultant force about a point where moment is taken.
Use:- This theorem is useful to calculate or find the position or location of Resultant of non-concurrent force system.
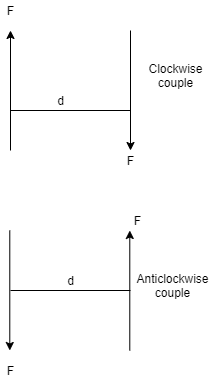
A pair of two equal and opposite (unlike) parallel forces (of same magnitude) is known as couple.
Properties of Couple:-
1. Two unlike parallel, non-collinear forces of same magnitude will form couple.
2. Resultant of couple is always zero.
3. Moment of couple is product of one of the force & lever arm of couple.
M = F xd
Lever arm of couple = ḻlar distance betn couple forces.
4. Couple cannot be balanced by single force.
5. Couple can be balanced only by another couple of opposite nature.
6. Moment of couple is independent of moment centre. i.e. Ref. point is not required to take moment of couple.
|
A force of 15 N is applied at an angle of 600 to the edge of door as shown in figure. Find the moment of this force.
E
Solution:- Resolving force at point B & then taking the moment about point O, M0 = (15 Cos 60 x 0) + (15 Sin 60 x 0.8) = 0 + 10.39 M0 = 10.39 N.m
A 90 N force is applied to the control rod AB. Determine moment of this Force about point B. Solution:- As we don’t know perpendicular distance betn force & point ‘ B ’, Let us resolve the force into two components. X – Component of force Fx = 90 Cos 25 = 81.567 N Y – Component of force Fy = 90 Sin 25 = 38.036 Now taking moments about point B. MB = [Fx x (3 Sin 65)] - [Fy x (3 Cos 65)] MB = (81.65 x 2.72) – (38.036 x 1.27) = 221.843 – 48.31 MB = 173.53 N.m
Examples on Non concurrent forces & use of Varigon’s theorem
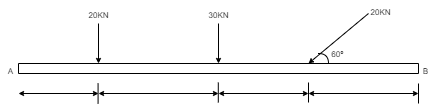
1. Determine the resultant of the system of forces acting on a beam as shown in figure.
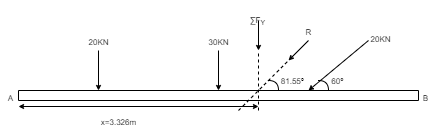
Above Force system is Non concurrent force system. Resolving the forces horizontally, ∑ Fx = - 20 Cos 60 = - 10 KN = 10 KN (towardleft) Resolving forces vertically, ∑Fy = - 20 – 30 – 20 Sin 60 = - 67.32 KN ∑Fy = 67.32 KN (downwards) Resultant, R = √ (∑ Fx) 2 + (∑Fy) 2 = √10 2 + 67.322 R = 68.06 KN Direction of Resultant, tanα = ∑Fy / ∑ Fx = 67.32 / 10.00 α = 81.550
Now taking moment about point A & using Varignon’s theorem. ∑MA = Moment of resultant A (20 x 1.5) + (30 x 3) + (20 Sin 60 x 6) = (∑ Fx x 0 ) + (∑Fyx X) 223.92 = 67.32 x X X = 223.92 / 67.32 = 3.326 m from point A
Ans
For a given force system, find the resultant in magnitude & direction. Also find the location of Resultant.
Solution
Resolving forces horizontally, ∑ Fx = - 15 + 25 Cos 40 = 4.15 N (toward right) Resolving forces vertically, ∑Fy = 25 Sin 40 – 10 = 6.07 n (upward) R = √(∑ Fx) 2 + (∑Fy)2 = √4.152 + 6.072 R = 7.35 N
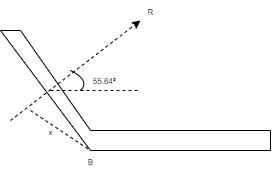
tanα = ∑Fy / ∑ Fx = 6.07 / 4.15 α= 55.640 - - - Angle made by resultant
To find exact position of R, let x is the perpendicular distance betn R & point B. Using Varignon’s theorem at point B. R x X = ∑MB = (10 x 150) – (15 x 150 Sin 50) + ( 25 x 375 ) – ( 6.25 x 1000 ) = 1500 – 1723.6 + 9375 – 6250 = 2901.4 N.mm (clockwise) x = 2901.4 / R = 2901.4 / 7.35 x = 394.75 mm from point B.
(Q) Find resultant moment of two couples for the loading as shown in Fig
Moment of 50 N couple is clockwise, = 50 x 1 = 50 N.m Moment of 100 N couple is also clockwise = 100 x 0.8 = 80 N.m.
Resultant Moment = 50 + 80 = 130 N.m
θ = tan-1 (3/4) = 36.860 with Horizontal Resolving forces in x & y dirn ∑ Fx = 20 – 50 Cosθ = 20 – 50 Cos 36.86 = - 20 N = 20 N
∑Fy = - 30 + 50 Sin 36.86 = 0.00007 ≈ 0
R = √(∑ Fx) 2 + (∑Fy)2 = 20 N toward left (as ∑ Fy = 0 ) Let us apply Varignons theorem at point B ∑MB = R.x ( 30 x 4 ) = Rx Rx = -120 N.m = 120 N.m As moment of Resultant is negative i.e. it is anticlockwise -Rx = -120 X = -120 / -20 = 6 m X = 6 m from point B and it will be above point. B to create anticlockwise moment.
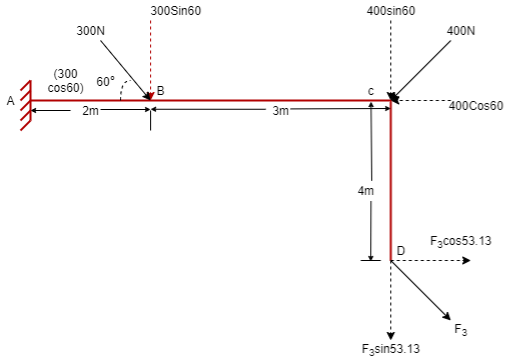
(Q) If the resultant moment about point A is 4800 Nm clockwise, determine the magnitude of F3 if F1 = 300 N and F2 = 400 N.
Given: Resultant Moment = 4800 N.m
Let us apply Varignon’s theorem at point A, ∑MB = (R.x )
[(300 60) x 2] + [(400 Sin 60) x 5] + [(F3 Sin 53.13 x 5)] – [(F3 Cos 53.13) x 4] = 4800 519.62 + 1732.05 + 3.99 F3 – 2.4 F3 = 4800 2251.67 + 1.59F3 = 4800 1.59 F3 = 2548.33
F3 = 2548.33 / 1.59 F3 = 2548.33 / 1.6 OR F3 = 1602.72 N F3 = 1592.7 N
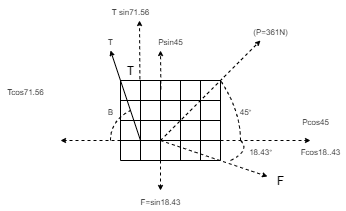
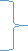
(Q) The three forces shown in Fig. create a vertical resultant acting through point B. If P = 361 N, compare the values of T and F.
From given figure, 1. Angle made by Force P is, = tan-1 (3/3) = 450 with Horizontal 2. Angle made by Force F is, = tan-1 (1/3) = 18.430 with Horizontal 3. Angle made by Force T is, = tan-1 (3/1) = 71.560 with Horizontal
Resolving forces along x & y dirn, As Resultant is vertical, let it is upward, then ∑ Fx = 0& ∑Fy = R
∑ Fx = P Cos 45 + F Cos 18.43 – T Cos 71.56 0 = 361 Cos 45 + F Cos 18.43 – T Cos 71.56 0 = 255.26 + 0.95 F – 0.32 T 0.95 F – 0.32 T = - 255.26 . . . . (1)
∑Fy = P Sin 45 – F Sin 18.43 + T Sin 71.56 R = 361 Sin 45 – F Sin 18.43 + T Sin 71.56 R = 255.26 – 0.32 F + 0.95 T …… (2)
Now as it is given that Resultant acts at point B, let us apply Varignon’s theorem at point B. ∑MB = R.x
But as R is acting at B point, its perpendicular distance from point B itself will be zero. ∑MB = R.x (P Cos 45 x 1) – (P Sin 45 x 2) + (T Cos 71.56 x 1) – (T Sin 71.56 x 1) – (F Cos 18.43 x 1) + (F Sin 18.43 x 2) = R x 0 As P = 361 N -255.26 – (255.26 x 2) + 0.32 T – 0.95 T – 0.95 F + (0.32 F x 2) = 0 -765.78 + 0.32 T – 0.95 T – 0.95 F + 0.64 F = 0 -765.78 – 0.63 T – 0.31 F = 0 – 0.31 F – 0.63 T = 765.78 . . . . (3) Solving eqn (1) and (3) simultaneously
-0.31 F – 0.63 T = 765.78
F = -581.716 N &
T = -929.282 N
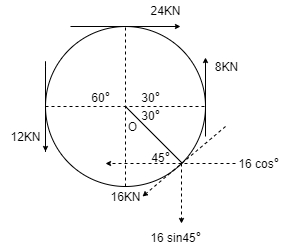
(Q) Determine the resultant of four forces tangent to the circle of radius 1.5 m as shown. Determine its location w.r.t. ‘O’.
Resolving forces in X and Y direction, ∑ Fx = 24 - 16 Cos 45 = 12.69 KN ( ) ∑Fy = -12 + 8 – 16 Sin 45 = -15.31 kN = 15.31 kN ( )
Resultant R = √(∑ Fx) 2 + (∑Fy)2 = √ 12.69 2 + (-15.31)2 R = 19.88 kN
Direction of Resultant, α = tan-1(∑Fy / ∑ Fx) α = tan-1(15.31 / 12.69) α = 50.350in 4th quadrant
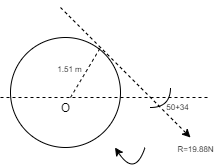
To know exact location of Resultant, let us apply Varignon’s theorem at point O. ∑MO = R.x -(12 x 1.5) + (24 x 1.5) – (8 x 1.5) + (16 x 1.5) = (19.88 x X) 30 = R.x As product of R.x is positive it means moment of Resultant is positive. To create positive clockwise moment of Resultant it must be acting on Right side of O (in 4th quadrant). 30 = 19.88 x X X = 1.51 m from O on the right hand side.
|
Resolution into two Parallel Components:- Case (a) two parallel components lies on either sides of force.
For this case, - Both components must have same direction as that of the original force. - Let P & Q are the two parallel component of force F, then P + Q = F - Using Varignon’s theorem we can find the magnitude of other force.
Case (b) when two components lies on one side of resultant.
- For this both components must have opposite direction. - Component near the force will have same direction as that of force (f). - Let P & Q are the components, then – P + Q = F. - Using Varignon’s theorem we can find magnitude of other force.
Examples on parallel forces & use of Varignon’s Theorem
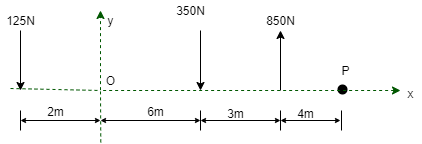
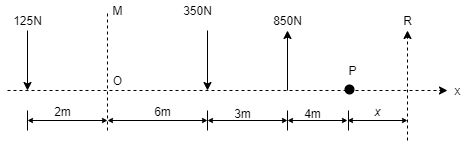
1. Replace the force system by single force resultant & specify its point of application measured along x-axis from point P. Refer the fig.
As forces are parallel & vertical, thus their x-component will be zero. To find resultant, ∑Fx = 0 ∑ Fy = -125 – 350 + 850 = 375 N (upward) R = √(∑ Fx) 2 + (∑Fy)2 = √0 + 3752 R = 375 N
As all forces are vertical, Resultant will also be vertical. i.e. α = 900 tanα = ∑Fy / ∑ Fx = 375 / 0 α = tan-1(∞) α= 900
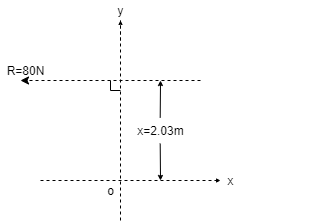
Thus R is vertical acting upward. Now using Varignon’s theorem about point P, R.x = (850 x 4) – (350 x 7) – (125 x 15) R.x = -925 Nm As moment of Resultant is –ve, it is anticlockwise. To produce anticlockwise moment about P, Resultant must act to the right of point P as shown in fig.
R.x = -925 N.m. -(375 x X) = -925 N.m. x = -925 / -375 x = 2.467 m from point P toward right.
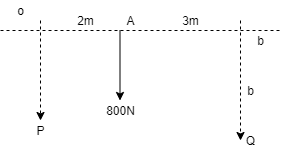
Resolve 800 N force at A into two parallel components P & Q acting respectively along (1) a-a & b-b(2) & c-c
Case (1) Resolution along a-a & b-b. Here force is betn two components thus both components must have same direction as that of force.
R = ∑Fy -800 = - P – Q 800 = P + Q …(1) Now taking moment at b-b & using Varignon theorem. (800 x 3) = -(P x 5) P = 800 x 3 / 5 P = 480 N downward
P + Q = 800 Q = 800 – 480 Q = 320 N downward
Case (ii) Resolution along b-b & c-c.
Now two components lie on one side of Resultant force (800 N). Thus they must have opposite direction & the component near the 800 N will have same direction as that of 800 N force. R = ∑Fy = - Q + P -800 = - Q + P --(ii)
Now taking moment at b-b & using Varignon’s theorem. -(800 x 3) = -(Q x 2) -2400 / 2 = Q Q = 1200 N . . . downward -800 = - Q + P -800 = - 1200 + P P = 400 N upward
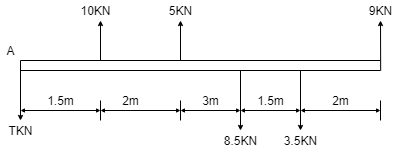
(Q) Find the resultant of following force system and also locate it from point A.
As all forces are vertical, ∑ Fx = 0 Resolving forces vertically, ∑Fy = - 7 + 10 + 5 – 8.5 – 3.5 + 9 ∑Fy = 5 KN (upward)
Resultant, R = √(∑ Fx) 2 + (∑Fy)2 = √(∑Fy)2 . . . . As ∑ Fx = 0
R = ∑ Fy R = 5 KN (upward) &α= 900 Now using Varignon’s theorem at point A ∑MA = R.x -(10 x 1.5) – (5 x 3.5) + (8.5 x 6.5) + (3.5 x 8) – (9 x 10) = R.x -39.25 KN.m = R.x R.x = 39.25 KN.m (Anticlockwise) 5 x X = 39.25 X = 39.25 / 5 = 7.85 m from point A. X = 7.85 m from A
(4) Determine the resultant of the parallel force system as shown in figure & locate it w.r.t. ‘ O . Radius of circle is = 1 m.
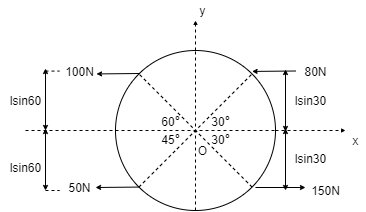
As all forces are Horizontal, ∑Fy = 0 Resolving forces horizontally, ∑Fx = -100 – 50 – 80 + 150 ∑Fx = - 80 N ∑Fx = 80 N (towardsleft)
As ∑Fy = 0 thus, R = ∑Fx Resultant = R = 80 N (towards left) To find exact location of R, use Varignon’s theorem at point ‘ O ’. ∑MO = R.x -(100 x Sin 60) + (50 x Sin 45) – (150 x Sin 30) – (80 x Sin 30) = R.x
-166.25 N.m (Anticlockwise)=R.x R.x = 166.25 80 x X = 166.25 X = 166.25 / 80 X = 2.08 m
|
Reference Books
1. Engineering Mechanics by S. P. Timoshenko and D. H. Young, McGraw- Hill publication
2. Engineering Mechanics by J. L. Meriam and Craige, John Willey
3. Engineering Mechanics by F L Singer, Harper and Rowe publication
4. Engineering Mechanics by A. P. Boresi and R. J. Schmidt, Brooks/Cole Publication