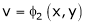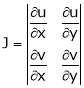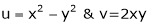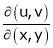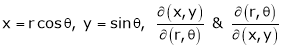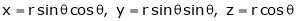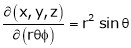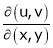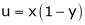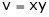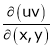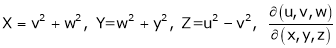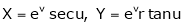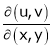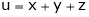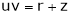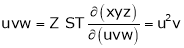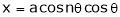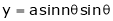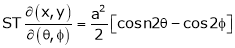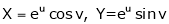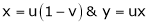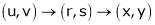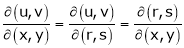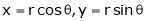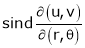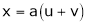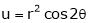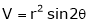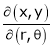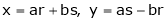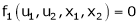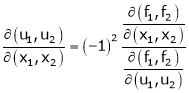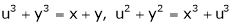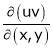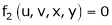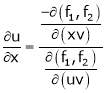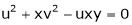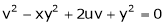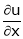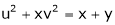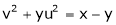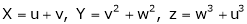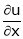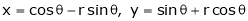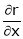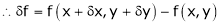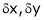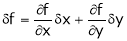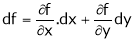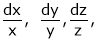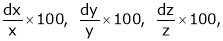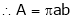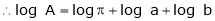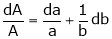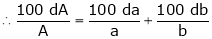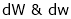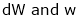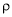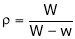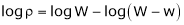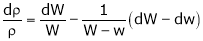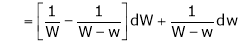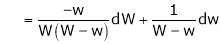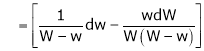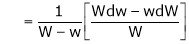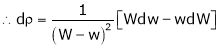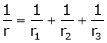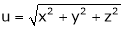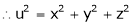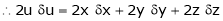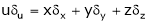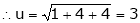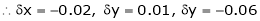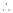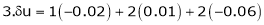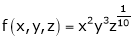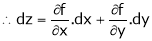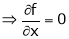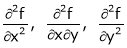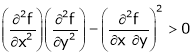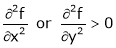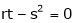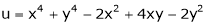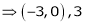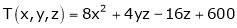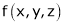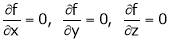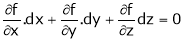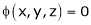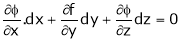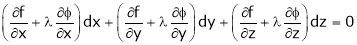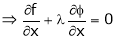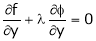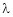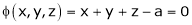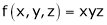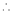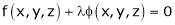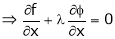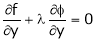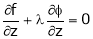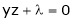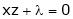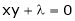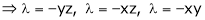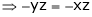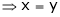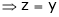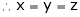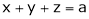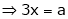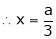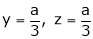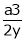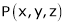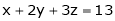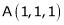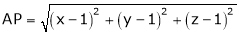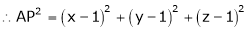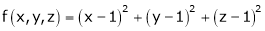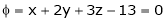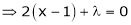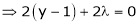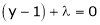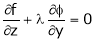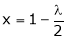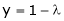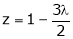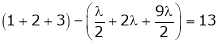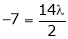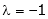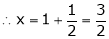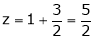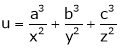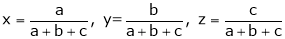Unit - 4
Applications of Partial Differentiation
If u and v be continuous and differentiable functions of two other independent variables x and y such as
Similarly , JJ’ = 1
Actually Jacobins are functional determines Ex.
ST 4. 5. If 6. 7. If 8. If JJ1 = 1 If
JJ1=1 Jacobian of composite function (chain rule)
Then Ex.
Where
2. If
Find 3. If
Find
Jacobian of Implicit function
Ex. If
If Find
Partial derivative of implicit functions
Ex. If Find If Find
Find
If Find
|
Let f(x, y) be a continuous function of x & y. Let
Expanding above expression by taylor’s theorem & since
i.e. Similarly, If f be a function of variables x, y, z, t, ………. Then we have
Note that
Ex. Q1) Find the percentage error in the area of an ellipse where error of ly is made in measuring it’s major and minor axes. S1)
Q2) The density S2)
Q3) Find the percentage error in computing the parallel resistance r of three resistances r1, r2, r3 from the formula.
Where r1, r2, r3 are each in error of 1 & 2y.
Q4) Find the approximate value of S4)
|
Note that
Ex. Discuss the stationary values of
Ex. Find the values of x and y for which x2 + y2 + 6x = 12 has a minimum values and find its minimum value.
Divide 120 into three parts so that the sum of their product. Taken two at a times shall be maximum. Using Lagrange’s method divide 24 into three parts. Such that continued product of the first, square of second, cube of third may be maximum. Find the maximum and minimum value of x2 + y2 when 3x2 + 4xy + 6y2 = 140
|
Let |
Let |
|
|
i.e. |
Also from |
|
Let ‘ |
|
|
|
|
Solving equation (3), (4) (5) & we get values of x, y, z and |
|
Q1) Decampere a positive number ‘a’ in to three parts, so their product is maximum
S1)
Let x, y, z be the three parts of ‘a’ then we get. |
|
Here we have to maximize the product |
i.e. |
|
|
|
|
|
i.e. |
|
|
|
|
|
|
And |
|
|
From (1) |
|
|
|
Thus |
Hence their maximum product is |
|
Q2) Find the point on plane 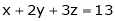 nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
nearest to the point (1, 1, 1) using Lagrange’s method of multipliers.
S2)
Let |
|
|
|
Under the condition |
|
|
|
|
|
i.e. |
|
|
From (2) we get |
From (3) we get |
From (4) we get |
|
|
i.e. |
|
|
|
|
y = 2 |
|
If |
Prove that the stationary value of u is given by, |
|
|
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I & Vol. II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Linear Algebra –An Introduction, Ron Larson, David C. Falvo (Cenage Learning, Indian edition)