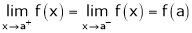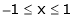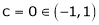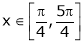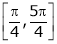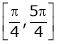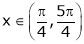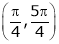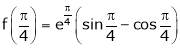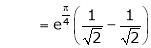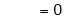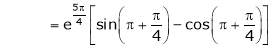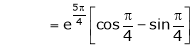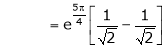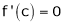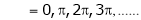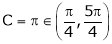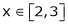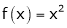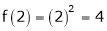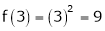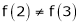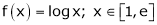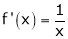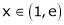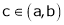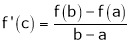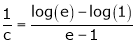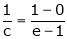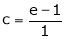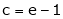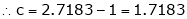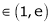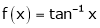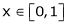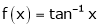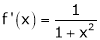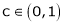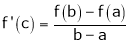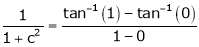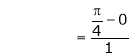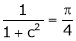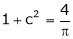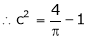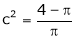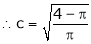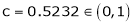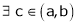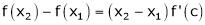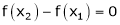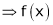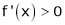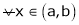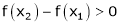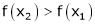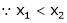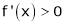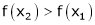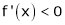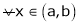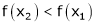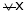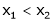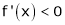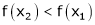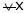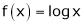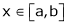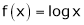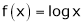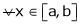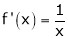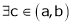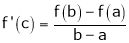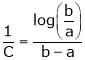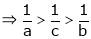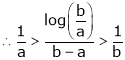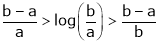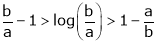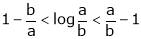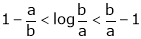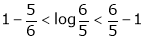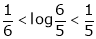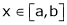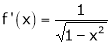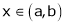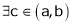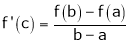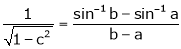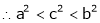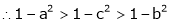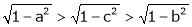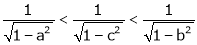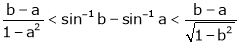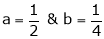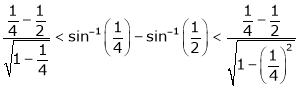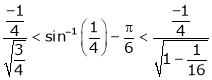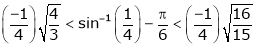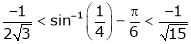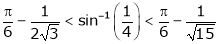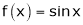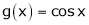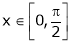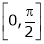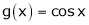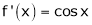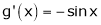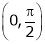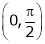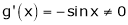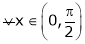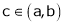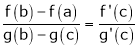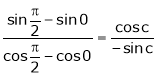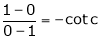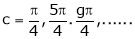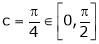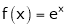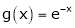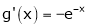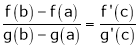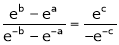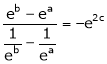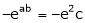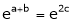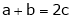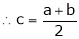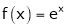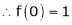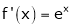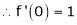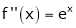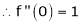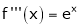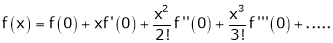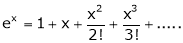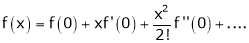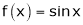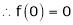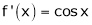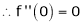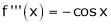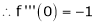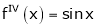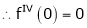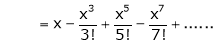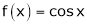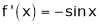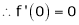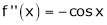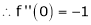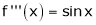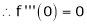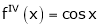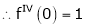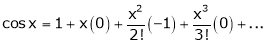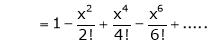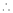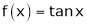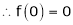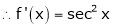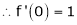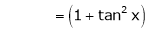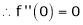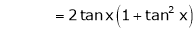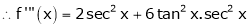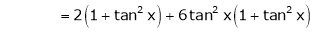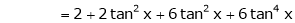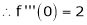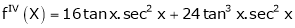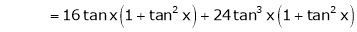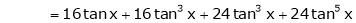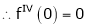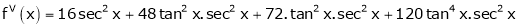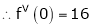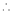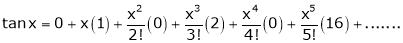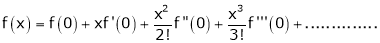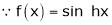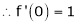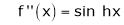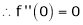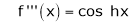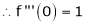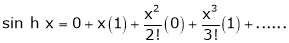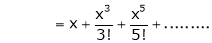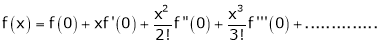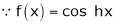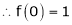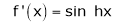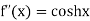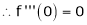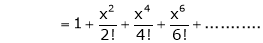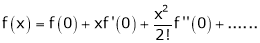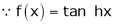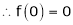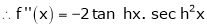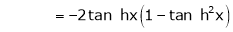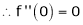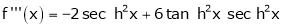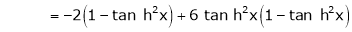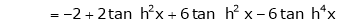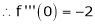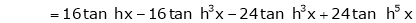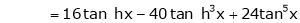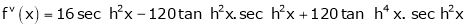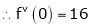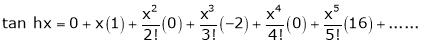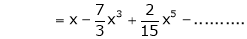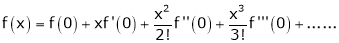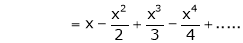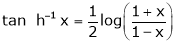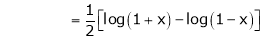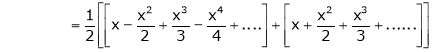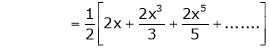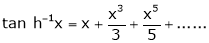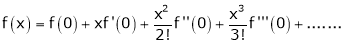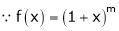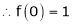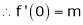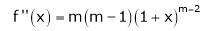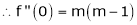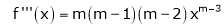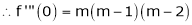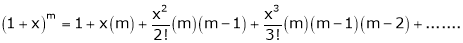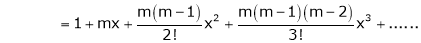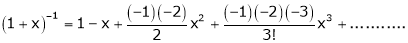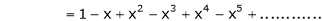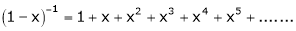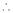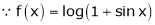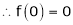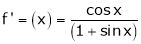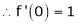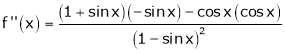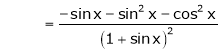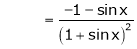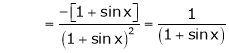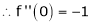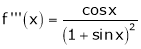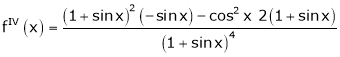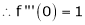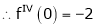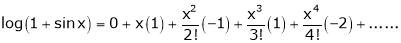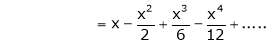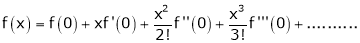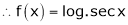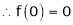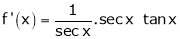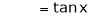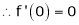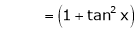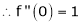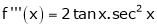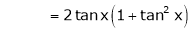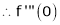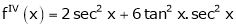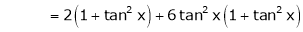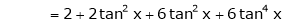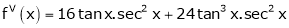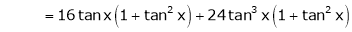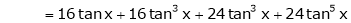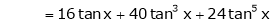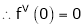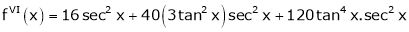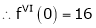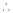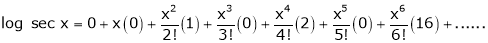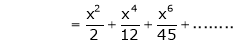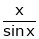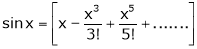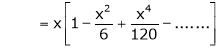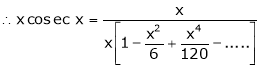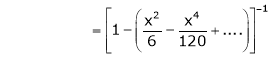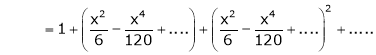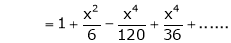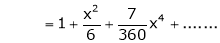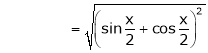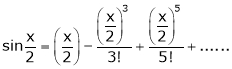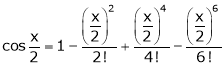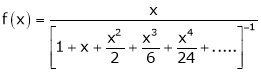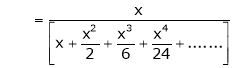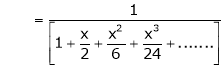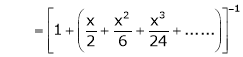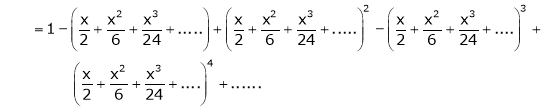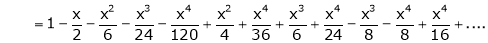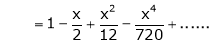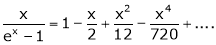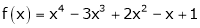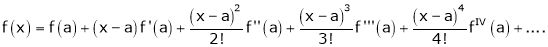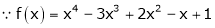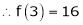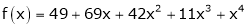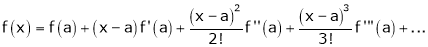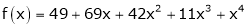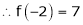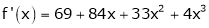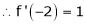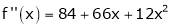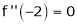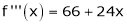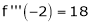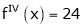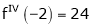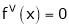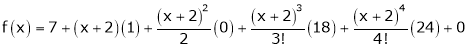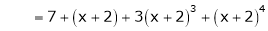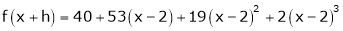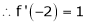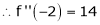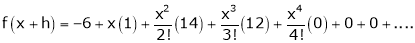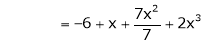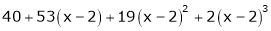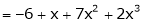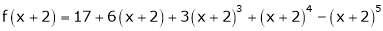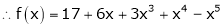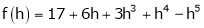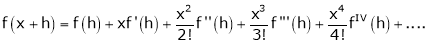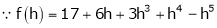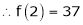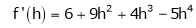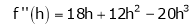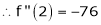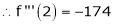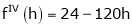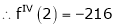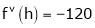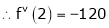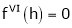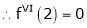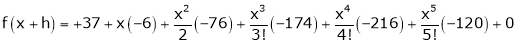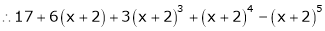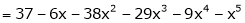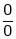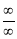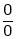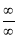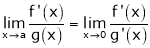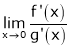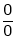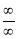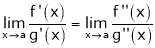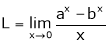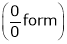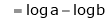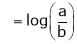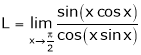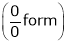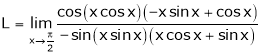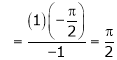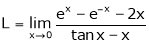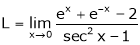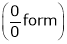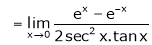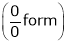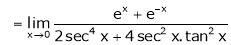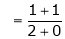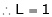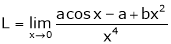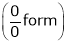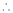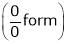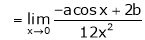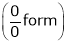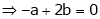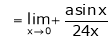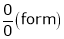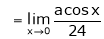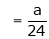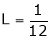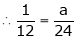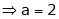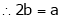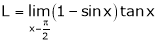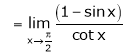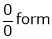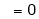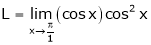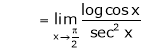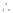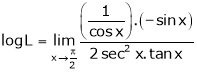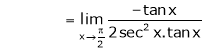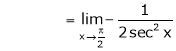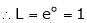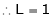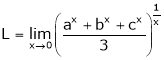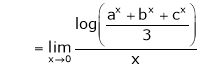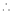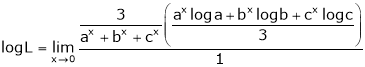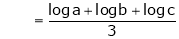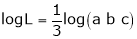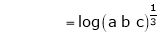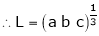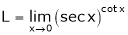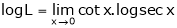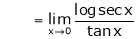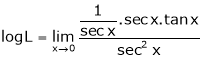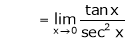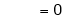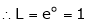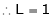UNIT 1
Differential Calculus
Continuous Function
A function f(x) is said to be continuous at x = a if
f(a) exist is function must exist at x = a
Differentiation
Let y = f(x) be any function A function f(x) is said to be differentiable at x = a if
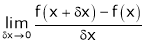 is exist and it is denoted by
is exist and it is denoted by 
Note:-
A differentiable function is always continuous but converse need not be true.
If
f(x) is continuous in the closed [a, b]
f(x) is differentiable in (a, b) &
f(a) = f(b)
Then there exist at least one value ‘c’ in (a, b) such that f’(c) = 0.
Q1)Verify Rolle’s theorem for the function f(x) = x2 for 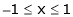
S1)
Here f(x) = x2; |
Since f(x) is algebraic polynomial which is continuous in [-1, 1] |
Consider f(x) = x2 |
a) Diff. w.r.t. x we get |
b) f'(x) = 2x |
Clearly f’(x) exist in (-1, 1) and does not becomes infinite. |
Clearly |
f(-1) = (-1)2 = 1 |
f(1) = (1)2 = 1 |
|
Hence by Rolle’s theorem, there exist |
f’(c) = 0 |
i.e. 2c = 0 |
|
Thus |
f'(c) = 0 |
Hence Rolle’s Theorem is verified. |
|
Q2) Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 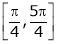
S2)
Here f(x) = ex(sin x – cos x); |
Clearly ex is an exponential function continuous for every |
Consider |
f(x) = ex(sin x – cos x) |
diff. w.r.t. x we get |
f’(x) = ex(cos x + sin x) + ex(sin x + cos x) |
= ex[2sin x] |
Clearly f’(x) is exist for each |
Hence f(x) is differentiable in |
Consider |
|
|
|
Also, |
|
|
|
|
|
|
Thus |
Hence all the conditions of Rolle’s theorem are satisfied, so there exist |
|
i.e. |
i.e. sin c = 0 |
|
|
But |
|
Hence Rolle’s theorem is verified. |
Q3) Verify whether Rolle’s theorem is applicable or not for
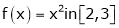
S3)
Here f(x) = x2; |
Clearly x2 is an algebraic polynomial hence it is continuous in [2, 3] |
Consider |
|
|
Clearly f’(x) is exist for each |
Consider |
|
|
Thus |
Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3] |
Q4)
a) Show that between any two real root of equation 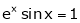 , is at least one real root of
, is at least one real root of 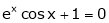 .
.
b) Discuss the applicability of Rolle’s theorem for the function
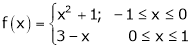
Lagrange’s Mean value Theorem:-
Statement:- If
f(x) is continuous in [a, b]
f(x) is differentiable in (a, b) then there exist at least one value  such that
such that
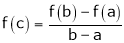
Q5) Verify the Lagrange’s mean value theorem for
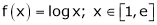
S5)
Here |
Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e] |
Consider f(x) = log x. |
Diff. w.r.t. x we get, |
|
Clearly f’(x) is exist for each value of |
Hence all conditions of LMVT are satisfied Hence at least |
Such that |
|
i.e. |
i.e. |
i.e. |
i.e. |
since e = 2.7183 |
|
Clearly c = 1.7183 |
Hence LMVT is verified. |
|
|
Q6) Verify mean value theorem for f(x) = tan-1x in [0, 1]
S6)
Here |
Clearly |
Consider |
diff. w.r.t. x we get, |
|
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite |
Hence all conditions of LMVT are satisfied, Thus there exist |
Such that |
|
i.e. |
|
i.e. |
i.e. |
|
i.e. |
|
|
Clearly |
Hence LMVT is verified. |
|
Meaning of sign of Derivative: |
Let f(x) satisfied LMVT in [a, b] |
Let x1 and x2 be any two points laying (a, b) such that x1 < x2 |
Hence by LMVT, |
i.e. |
Cast I: |
If |
i.e. |
|
Case II: |
If |
|
i.e. |
|
Thus for x2 > x1 |
|
Thus f(x) is increasing function is (a, b) |
Case III: |
If |
Then from equation (1) |
|
i.e. |
since |
|
Q7) Prove that
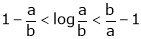
And hence show that
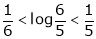
S7)
Let |
Clearly |
Consider |
diff. w.r.t. x we get, |
|
Clearly f’(x) exist and finite in (a, b) Hence f(x) is continuous and differentiable in (a, b). Hence by LMVT |
Such that |
|
i.e. |
i.e. |
since |
a < c < b |
|
|
i.e. |
i.e. |
i.e. |
i.e. |
Hence the result |
Now put a = 5, b = 6 we get |
|
|
Hence the result |
Q8) Prove that 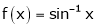 ,
, 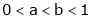 use mean value theorem to prove that,
use mean value theorem to prove that,
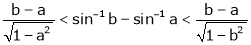
Hence show that

S8)
Let f(x) = sin-1x; |
Clearly f(x) is inverse trigonometric function and hence it is continuous in [a, b] |
Consider f(x) = sin-1x |
diff. w.r.t. x we get, |
|
Clearly f’(x) is finite and exist for |
|
i.e. |
since a < c < b |
|
|
i.e. |
i.e. |
i.e. |
i.e. |
Hence the result |
Put |
|
i.e. |
i.e. |
i.e. |
i.e. |
Hence the result |
Cauchy’s Mean Value Theorem:
Statement:-
If f(x) and g(x) are any two functions such that
f(x) and g(x) are continuous in (a, b)
both f(x) and g(x) are derivable in (a, b)

Then for any value of 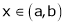 ,
, 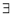 at least
at least 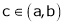 such that
such that
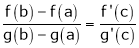
Q9)
Verify Cauchy mean value theorems for  &
& 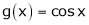 in
in 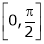
S9)
Let |
Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in |
Since |
diff. w.r.t. x we get, |
|
Clearly both f’(x) and g’(x) exist & finite in |
|
Hence by Cauchy mean value theorem, there exist at least |
|
i.e. |
|
i.e. 1 = cot c |
|
i.e. |
clearly |
Hence Cauchy mean value theorem is verified. |
|
Q10) Considering the functions ex and e-x, show that c is arithmetic mean of a & b.
Solution:
Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b]. |
Consider |
diff. w.r.t. x we get |
|
Clearly f(x) and g(x) are derivable in (a, b) |
|
|
i.e. |
i.e. |
i.e. |
i.e. |
i.e. |
i.e. |
|
Thus |
i.e. c is arithmetic mean of a & b. |
Hence the result |
|
Q11) Show that 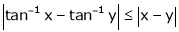
Prove that if 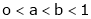
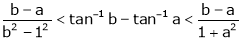 and Hence show that
and Hence show that
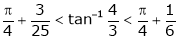
Verify Cauchy’s mean value theorem for the function x2 and x4 in [a, b] where a, b > 0
If for 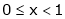 then prove that,
then prove that,
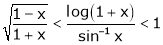
[Hint: ,
, 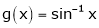 ]
]
Expansions of functions
In this topic we learn two important series expansions namely
a) Maclaurin’s series
b) Taylors Series
Maclaurin’s Series Expansions
Statement:-
Maclaurin’s series of f(x) at x = 0 is given by,
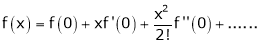
Expansion of some standard functions
1) f(x) = ex then
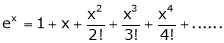
Proof:-
Here |
|
|
|
|
|
|
i.e. |
Note that |
1) Replace x by –x we get |
|
2) f(x) = sin x then
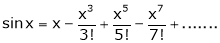
Proof: |
Let (x) = sin x |
Then by Maclaurin’s series, |
|
Since |
|
|
|
|
|
|
|
|
3)
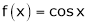 Then
Then

Proof: |
Let f(x) = cos x |
Then by Maclaurin’s series, |
|
Since |
|
|
|
|
|
|
|
|
|
4) 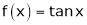 then
then
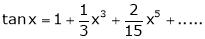
Proof: |
Here f(x) = tan x |
|
|
Since |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) 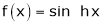 Then
Then
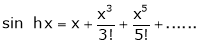
Proof:- |
Here f(x) = sin hx. |
|
|
|
|
|
|
|
|
|
6) 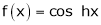 . Then
. Then
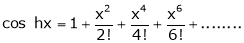
Proof:- |
Here f(x) = cos hx |
|
|
|
|
|
|
|
|
|
7) f(x) = tan hx
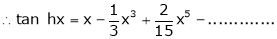
Proof: |
Here f(x) = tan hx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8)  then
then
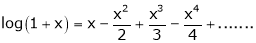
Proof:- |
Here f(x) = log (1 + x) |
|
|
|
|
|
|
|
|
|
|
9) 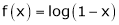
In above result we replace x by -x
Then
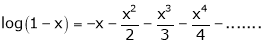
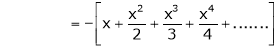
10) Expansion of tan h-1x
We know that |
|
|
|
|
|
Thus |
|
11)Expansion of (1 + x)m
Proof:- |
Let f(x) = (1 + x)m |
|
|
|
|
|
|
|
|
|
|
Note that in above expansion if we replace m = -1 then we get, |
|
|
Now replace x by -x in above we get, |
|
|
Expand by, Maclaurin’s theorem
Q1) 
S1)
Here f(x) = log (1 + sin x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Expand by Maclaurin’s theorem,
log sec x
Solution:
Let f(x) = log sec x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Prove that 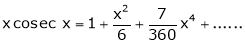
Solution:
Here f(x) = x cosec x |
= |
Now we know that |
|
|
|
|
|
|
|
|
|
Expand  upto x6
upto x6
Solution:
Here |
|
|
|
Now we know that |
|
|
Adding (1) and (2) we get |
|
Show that 
Solution:
Here |
|
|
|
|
|
|
|
Thus |
|
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is

b) The expansion of f(x+h) in ascending power of h is
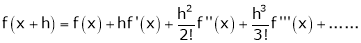
c) The expansion of f(x) in ascending powers of (x-a) is,

d) Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions
Expand 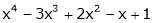 in power of (x – 3)
in power of (x – 3)
Solution:
Let |
Here a = 3 |
Now by Taylor’s series expansion, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Using Taylors series method expand
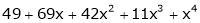 in powers of (x + 2)
in powers of (x + 2)
Solution:
Here |
a = -2 |
|
|
Since |
|
|
|
|
|
|
|
|
|
|
Thus equation (1) becomes |
|
|
|
Expand 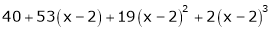 in ascending powers of x.
in ascending powers of x.
Solution:
Here |
|
i.e. |
|
Here h = -2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Thus |
|
|
|
Expand 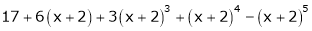 in powers of x using Taylor’s theorem,
in powers of x using Taylor’s theorem,
Solution:
Here |
|
|
i.e. |
Here |
h = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exercise
a) Expand 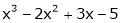 in powers of (x – 2)
in powers of (x – 2)
b) Expand 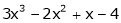 in powers of (x + 2)
in powers of (x + 2)
c) Expand 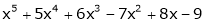 in powers of (x – 1)
in powers of (x – 1)
d) Using Taylors series, express 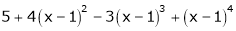 in ascending powers of x.
in ascending powers of x.
e) Expand 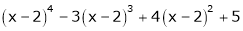 in powers of x, using Taylor’s theorem.
in powers of x, using Taylor’s theorem.
Consider
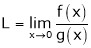
Then limit of f(x) and g(x) both are zero when 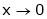 then
then
L becomes 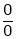 form.
form.
This form is called indeterminate form. The other indeterminate formal are  ,
,  ,
, 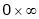 ,
, 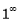 , OO,
, OO, 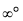 etc.
etc.
To evaluate limit in this case we use L – Hospital rule
L – Hospital rule for |
Statement: |
If |
Indeterminate form, then |
|
If |
Then |
We continue the procedure until the limit is exist. |
Q1) Evaluate 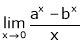
S1)
Let |
|
|
|
|
|
Q2) Evaluate 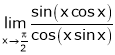
S2)
Let |
|
|
|
|
Q3) Evaluate 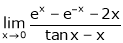
S3)
Let |
|
|
|
|
|
|
|
|
Q4) Find the value of a, b if 
S4)
Let |
|
|
|
|
|
|
|
|
But |
|
|
|
|
|
|
|
Q5) Evaluate 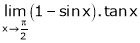
S5)
Let |
|
|
|
|
|
Q6) Evaluate 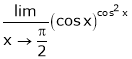
S6)
Let |
|
Taking log on both sides we get, |
|
|
|
i.e. |
|
|
|
|
|
|
Q7) Evaluate 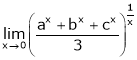
S7)
Let |
|
|
|
|
|
|
|
i.e. |
|
|
|
Q8) Evaluate 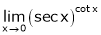
S8)
Let |
|
|
|
|
|
|
|
|
|
|
|
|
Exercise
Evaluate the following limits.
a) 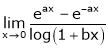
b) 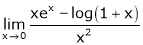
c) 
d) 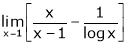
e) 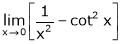
f) 
g) 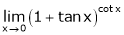
h) 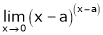
i) 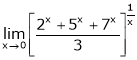
j) 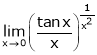
a) Find the value of a, b, c if 
b) If 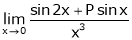 is finite then find the value of p and hence the value of the limit.
is finite then find the value of p and hence the value of the limit.
c) Find the value of a, b if, 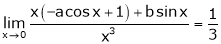
d) Find the value of a and b if, 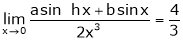
e) Find the value of a and b if, 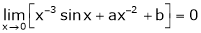
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I & Vol. II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Linear Algebra –An Introduction, Ron Larson, David C. Falvo (Cenage Learning, Indian edition)