Unit 1
Basic Electrical
It is equal to the terminal potential difference when no current flows. Its unit is volts. EMF is the amount of energy (E) provided by the battery to each coulomb of charge (Q) passing through.
It is also known as voltage. It is defined as the amount of work done to move a unit charge from one point to another. It is measured in volts.
V= W/Q
W= work done
Q=charge
Current:
The rate of flow of charge across a cross-section of the conducting material is called as current.
i = 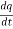
q= charge in coulombs
t= time in seconds
Power: The rate at which energy is generated. It is energy per unit time. Units is watt.
P= E/t
Energy: It is work done by a force of one newton acting over a distance of one meter.
E= Fl
F=m*a
F= force
m=mass
a=acceleration
Ohms Law: It states that the current through the conductor between two points is directly proportional to the voltage across the two points
V α I
V= IR
V = voltage across terminals in volts
R = resistance in ohms
I= current in Amperes
Categories of sources
- Voltage source and current source
- A.C. Source and D.C. Source
- Dependent source and independent source
- Constant and function of time source
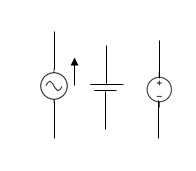
few either
AC or DC 
dc
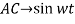
Equivalent circuit diagram of
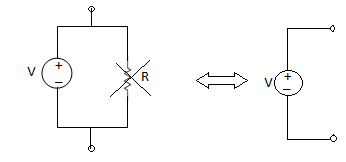
- Voltage Source: A voltage source always have a resistance in series.
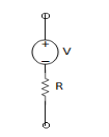
Ideal source
R = 0
Practical = 2 - 5Ω
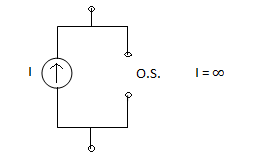
I = 0
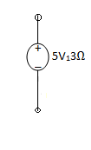
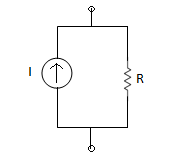
2. Current Source: Always have R parallel with the source.

Ideal and practical Voltage and Current source:
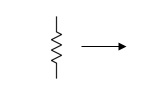
A voltage source is a device which provides a constant voltage to load at any instance of time and is independent of the current drawn from it. This type of source is known as an ideal voltage source. Practically, the ideal voltage source cannot be made. It has zero internal resistance. It is denoted by this symbol.
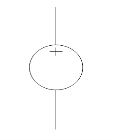
Fig: Voltage source symbol
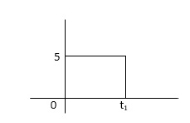
Ideal Voltage Source
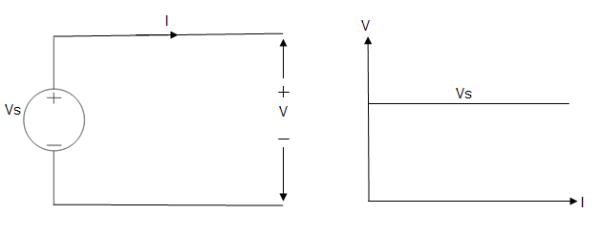
Fig: Ideal Voltage Source
The graph represents the change in voltage of the voltage source with respect to time. It is constant at any instance of time.
Voltage sources that have some amount of internal resistance are known as a practical voltage source. Due to this internal resistance, voltage drop takes place. If the internal resistance is high, less voltage will be provided to load and if the internal resistance is less, the voltage source will be closer to an ideal voltage source. A practical voltage source is thus denoted by a resistance in series which represents the internal resistance of source.
Practical Voltage source
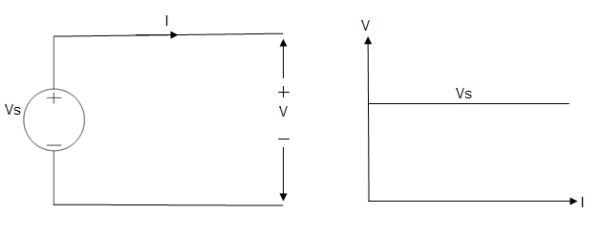
Fig: Practical Voltage source
The graph represents the voltage of the voltage source with respect to time. It is not constant but it keeps on decreasing as the time passes.
Current source
A current source is a device which provides the constant current to load at any time and is independent of the voltage supplied to the circuit. This type of current is known as an ideal current source; practically ideal current source is also not available. It has infinite resistance. It is denoted by this symbol.
Ideal Current source

Fig: Ideal Current source
The graph represents the change in current of the current source with respect to time. It is constant at any instance of time.
Why ideal Current source has infinite resistance?
A current source is used to power a load, so that load will turn on. We try to supply 100% of the power to load. For that, we connect some resistance to transfer 100% of power to load because the current always takes the path of least resistance. So, in order for current to go to the path of least resistance, we must connect resistance higher than load. This is why we have the ideal current source to have infinite internal resistance. This infinite resistance will not affect voltage sources in the circuit.
Practical Current source
Practically current sources do not have infinite resistance across there but they have a finite internal resistance. So the current delivered by the practical current source is not constant and it is also dependent somewhat on the voltage across it.
A practical current source is represented as an ideal current source connected with resistance in parallel.
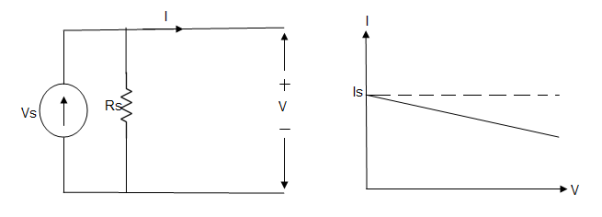
Fig; Practical Current source
The graph represents the current of the current source with respect to time. It is not constant but it also keeps on decreasing as the time passes.
Examples of current and voltage sources
The examples of current source are solar cells, transistors and examples of some voltage sources are batteries and alternators.
This was all about ideal and practical sources of power. The ideal sources are very useful for calculations in theory but as ideal sources are not practically possible, only practical sources are used in practical circuits. The batteries we use are a practical source of power and the voltage and current decreases as we use it. Thus both are useful to us in their own ways.

- From VI:

2. From IV:
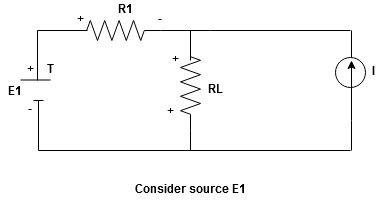
Statement : the response in any element of linear bilateral network containing more than on sources is the sum of the responses produced by the individual source acting alone. The responses means the voltage across the element or the current in the element The voltage sources should be replaced by short circuit and the current source must be replaced by open circuit .Steps to apply superposition theorem :
1.
Current sources should be open
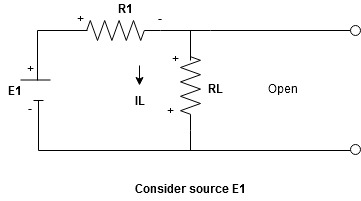
Find the current (IL1)(+) through or the voltage across the required element due to the source under consideration using a suitable n/w technique.
- Consider current source (I)Voltage source should be short circuit
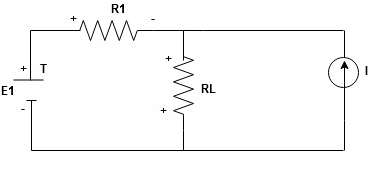
Find the current (ILII)(+) by a suitable network simplification technique
2. Add the individual current IL and ILII by the individual sources acting alone to find total current flowing in load resistance (RL)
Ie L =
L =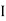 L
L +
+  L
L 
Resistor:-
Control the flow of current
V=IR
P=I2R

Behaviour of Resistance:-

t=0- t=0 t=0+ t=∞
R R R R

Resistance is affected by temperature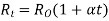
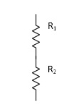
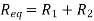
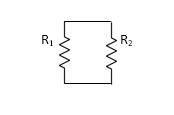
R1|| R2 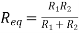
The algebraic sum of currents meeting at a junction or node in a electric circuit is zero ② or the summation of all incoming current is always equal to summation of all outgoing current in an electrical network.
Explanation
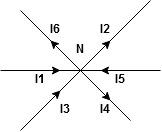
Assuming the incoming current to be positive and outgoing current negative we have
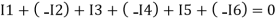
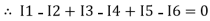
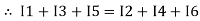
Ie incoming current = ∑ outgoing current thus, the above Law can also be stated as the sum of current flowing towards any junction in an electric circuit is equal to the sum of currents flowing away from that junction
incoming current = ∑ outgoing current thus, the above Law can also be stated as the sum of current flowing towards any junction in an electric circuit is equal to the sum of currents flowing away from that junction
Kirchhoff’s Voltage Law (KVL)
Statement : the algebraic summation of all Voltage in any closed circuit or mesh of loop zero.
Ie ∑ Voltage in closed loop = 0 the summation of the Voltage rise (voltage sources) is equal to summation of the voltage drops around a closed loop in 0 circuit for explanation from here
Determination of sigh and direction of currents (Don’t write in exams just for understanding)
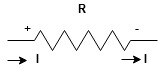
Current entering a resistor is +ve and leaving should be –ve
Now
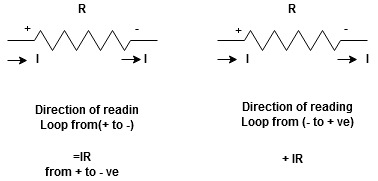
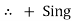
Potential Rise Potential Drop
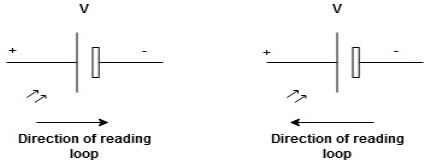
We are reading from +V to –V we are reading from –V to +V
 potential drops
potential drops  potential rise
potential rise
 -V
-V  +V
+V
Given Circuit
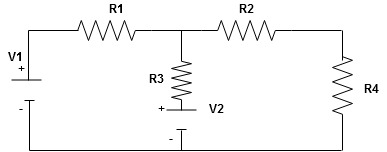
First identify no of loops and assign direction of current flowing in loop
Note : no of loops in circuit = No, of unknown currents = no, of equations in the circuit
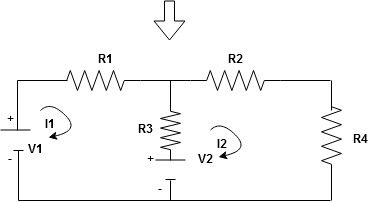
Note : keep loop direction and current direction same ie either clockwise or anticlockwise for all loops I1 I2
Now according to direction of direction assign signs (+ve to –ve) to the resistors
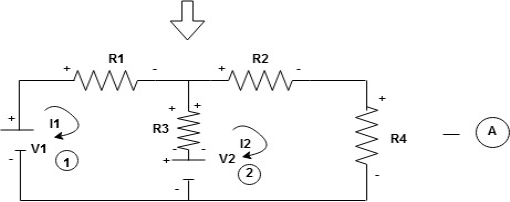
Note : voltage sources (V) polarities does not change is constant.
Note: for common resistor between 2 loops appearing in the circuit like R3 give signs according to separate loops as shown
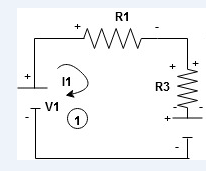
When considering only loop no 1 (+ R3 - )
- B
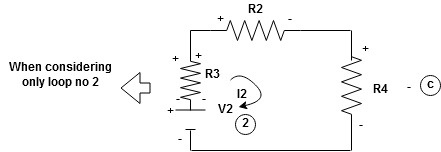
Now consider diagram A and write equations
Two loops  two unknown currents
two unknown currents  two equation
two equation
Apply KVL for loop ① [B. Diagram ]
(+ to drop -) = - sign and (- to rise +) = + sign
 for drop = -sign
for drop = -sign
 for rise = + sign
for rise = + sign
-
-(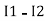 ) R2 is considered because in R3,2 currents are flowing
) R2 is considered because in R3,2 currents are flowing 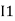 and
and 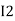 and we have taken (
and we have taken (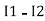 ) because we are considering loop no 1 and current flowing is
) because we are considering loop no 1 and current flowing is 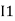 in loop no 1
in loop no 1
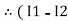 )
)
Similarly for loop no. 2 currents flowing is 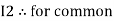 resistor R3 it should be
resistor R3 it should be 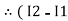 )R3
)R3
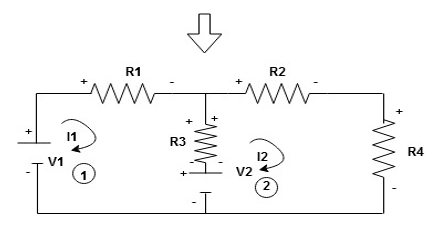
Consider loop no. 1 apply KVL
-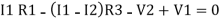 …….①
…….①
-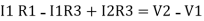
Consider loop no. 2 apply KVL
- …….②
…….②
-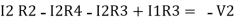
After solving equation ① and ② we will get branch current 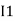 and
and 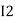
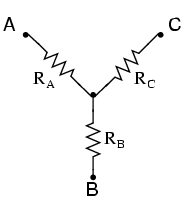
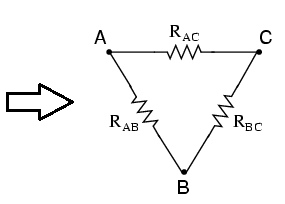
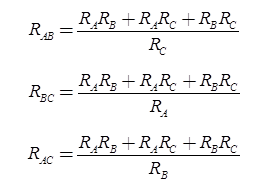
Inductor
- Active - FET, diode
- Passive - R, L, C
Storage of energy
Based on electromagnetic induction
Faraday’s Law
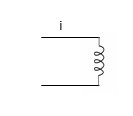
Φ∝i
Φ = L.i
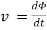
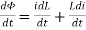

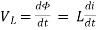
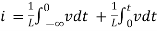
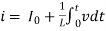
Relaxed inductor I0 = 0

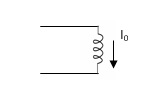
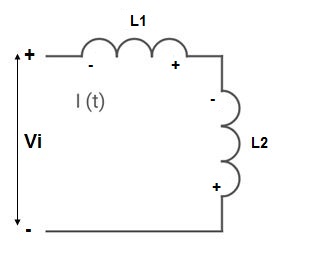
Current Carrying Inductor:
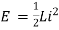
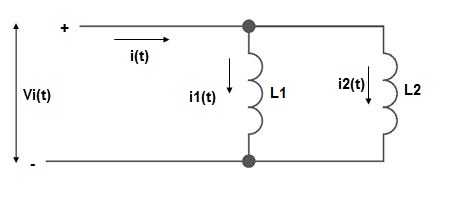
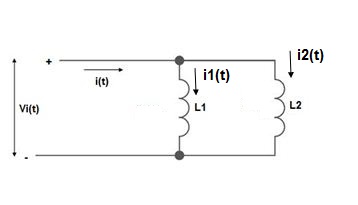
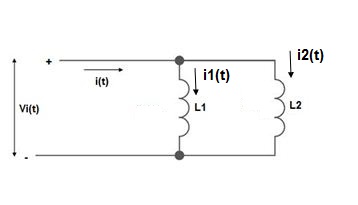
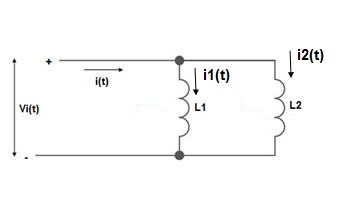
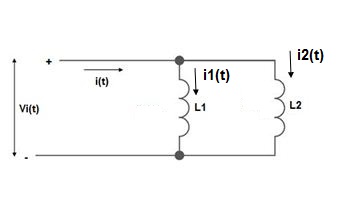
L = L1+L2

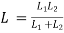
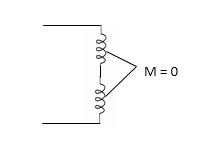
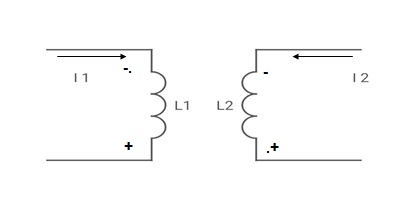
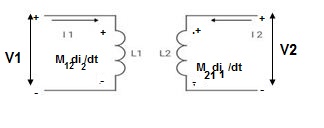
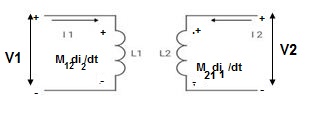
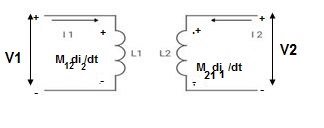
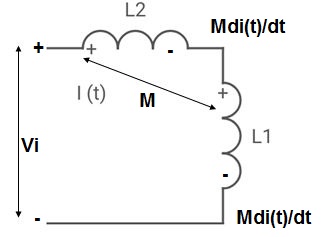
MUTUAL INDUCTANCE:-
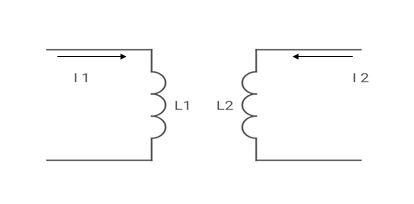
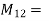 mutual inductance on 1 due to 2
mutual inductance on 1 due to 2
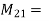 mutual inductance on 2 due to 1
mutual inductance on 2 due to 1
● If current is entering at dot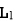 then it will produce mutual induction or it will produce a voltage with positive polarity on
then it will produce mutual induction or it will produce a voltage with positive polarity on 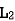 .
.
● If current is leaving at dot then it will produce a voltage with negative polarity on
then it will produce a voltage with negative polarity on 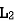 .
.
Voltage on 2 due to 1 = 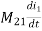
Voltage on 1 due to 2 = 
- When current is entering or leaving from both dots.
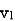 -
- 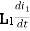 -
- 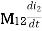 = 0 ⎼⎼⎼⎼⎼⎼ 1
= 0 ⎼⎼⎼⎼⎼⎼ 1
 -
- 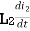 -
- 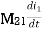 = 0 ⎼⎼⎼⎼⎼⎼2
= 0 ⎼⎼⎼⎼⎼⎼2
 -
- 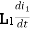 -
- 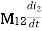 = 0 ⎼⎼⎼⎼⎼⎼⎼1
= 0 ⎼⎼⎼⎼⎼⎼⎼1
 -
- 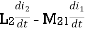 = 0 ⎼⎼⎼⎼⎼⎼⎼2
= 0 ⎼⎼⎼⎼⎼⎼⎼2
2. When current is entering from one dot and leaving the other
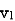 -
- 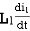 +
+ 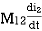 = 0 ⎼⎼⎼⎼⎼⎼⎼⎼1
= 0 ⎼⎼⎼⎼⎼⎼⎼⎼1
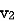 -
- 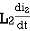 +
+  = 0 ⎼⎼⎼⎼⎼⎼⎼⎼2
= 0 ⎼⎼⎼⎼⎼⎼⎼⎼2
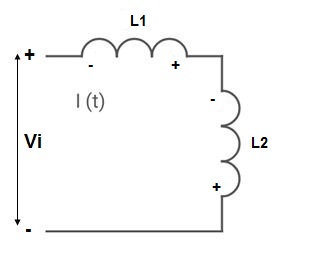
- When current is entering in both dots
Find 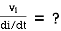
If 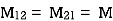
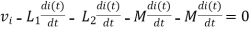
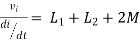
II. When current leaves both dots
 Find
Find 
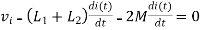
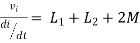
III. When current enters from  and leaves
and leaves 
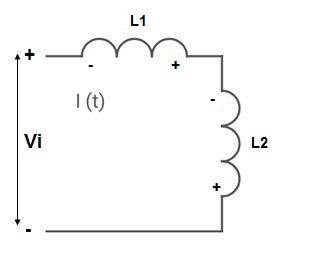 Find
Find 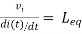
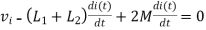
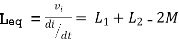
IV. When current leaves 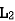 and enters
and enters 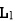
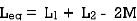
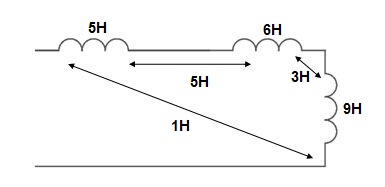
Example 1. Find 
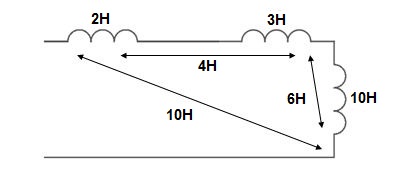
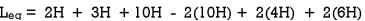
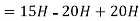
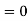
Example 2. Find 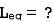

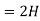
PARALLEL COMBINATION: -
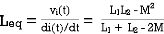
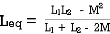
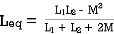

Charge storing device (voltage)
Q ∝ V
Q = C V
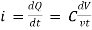
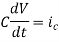
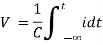
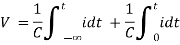

Relaxed capacitor 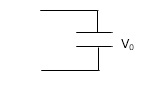
charged capacitor
Electrostatic Energy
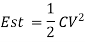
Inductor do not respond any change as far as current is concerned.
Capacitor does not respond any change as far as voltage is concerned.
Definition of Open circuit and short circuit
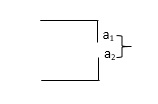
R=∞
V=0 or V≠ 0
I=0
Short Circuit:
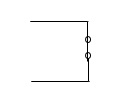
V = 0
R = 0
I may or may not be zero