Unit - 5
Turing Machine
An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
Formal definition
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ : alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of turing machine
With the help of the following representation, the turning machine can be modeled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.
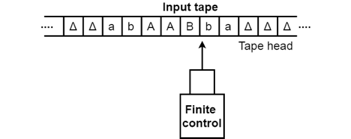
Fig 2: Basic model of TM
Various features of the Turing machine exist:
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
It consists of a head that reads the input tape.
A state register stores the state of the information processing system.
Even though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements.
Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.
Example: Creating a turing machine which accepts the language of aba over ∑ = {a, b}
Sol: We'll think that the string 'aba' is positioned like this on the input tape:
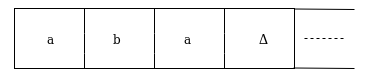
The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop.
Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:
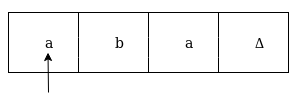
The next move are δ(q0, a) = δ(q1, A, R) which means it goes to state q1, replaced by A and head moves toward right :
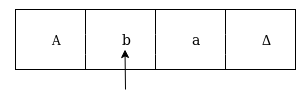
The next move are δ(q1, b) = δ(q2, B, R) which means it goes to state q2 , replaced by B and head moves toward right :
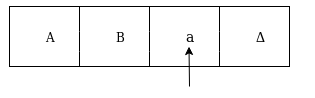
The next move are δ(q2, a) = δ(q3, A, R) which means it goes to state q3 , replaced by A and head moves toward right :
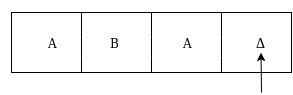
The move δ(q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine .
State | a | b | ᇫ |
q0 | (q1, A, R) | - | - |
q1 | - | (q2,B,R) | - |
q2 | (q3,A,R) | - | - |
q3 | - | - | (q4, ᇫ , S) |
q4 | - | - | - |
The turing machine can be represented by transition diagram –
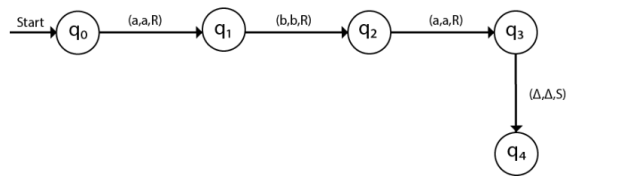
Fig 3: Transition diagram for turing machine
As a transducer, a Turing machine can be employed. The most apparent method to do this is to treat the full nonblank area of the first cassette as input, and the complete non blank piece of the second tape as output when the machine halts.
In other words, a Turing machine defines a function y=f(x) for strings x, y is a member of Σ * if
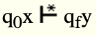
Where qf is a final state.
If a Turing machine can execute the given task, then a function f is Turing computable.
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, method of infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
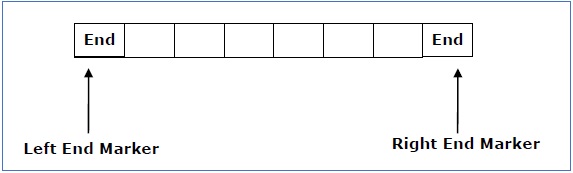
Fig 4: Linear bounded automata
The measurement is limited to the region bounded by constants.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.
Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.
δ(non-halting-state, symbol) = UNDEF
By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission
δ(R,σ) = (R,σ) ∀ σ ∈ Σ
Simply send a missing transition to this state without tape modification with this addition, i.e.,
δ(non-halting-state, symbol) = (R, symbol)
The easiest computer we can create that runs indefinitely is this:
RunForever = ( {s,h}, Σ, {}, s, {h} )
There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"
● Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
● Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
● Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Recursive language (RE) –
A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’. The computing device can halt on every occasion and provides associate answer (accepted or rejected) for every and each string input. A language ‘L’ is decidable if it’s a algorithmic language. All decidable languages area unit algorithmic languages and vice-versa.
Recursively countable language (RCE) –
A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.
By definition, all REC languages {are also|also area unit|are} RE languages however not all RE languages are REC languages.
A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing-Acceptable.
Fig 5: Each decidable language is Turing-Acceptable.
A decision downside P is decidable if the language L of all affirmative instances to P is decidable.
For a decidable language, for every input string, the thulium halts either at the settle for or the reject state as pictured within the following diagram –
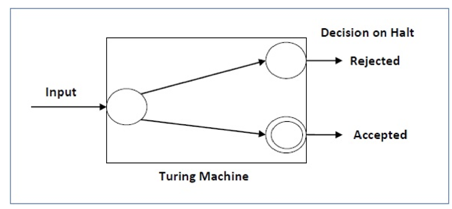
Fig 6: Turing machine
Key takeaway
A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’.
A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.
If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable. There is no technique for determining the answer to an undecidable problem for a given input.
We frequently come across similar situations in the theory of computation where the answer is either 'yes' or 'no.' Solvable or decidable problems are those that can be answered with a yes or no. Otherwise, the problem category is referred to as unsolvable or undecidable.
Example
Ambiguity of context-free languages: There is no Turing machine that, given a context-free language, will always halt in a finite amount of time and say whether the language is ambiguous or not.
Equivalence of two context-free languages: There is no Turing computer that, given two context-free languages, will always halt in a finite amount of time and say whether the languages are equal or not.
Everything or completeness of CFG: It is unclear whether CFG will generate all possible strings of input alphabet (*) given a CFG and input alphabet.
Regularity of CFL, CSL, REC and REC: It's impossible to say whether a CFL, CSL, REC, or REC is regular given a CFL, CSL, REC, or REC.
Undecidability of Universal Languages:
The universal communication system We must show that Lu is undecidable because it is a recursively enumerable language (non-recursive).
Theorem - Lu is a recursive but not a recursive RE.
Proof - Consider the fact that the language Lu is recursively enumerable. Lu will be assumed to be recursive. The complement of Lu, which is Lu, is recursive as well. We can, however, construct a TM Ld if we have a TM M that accepts Lu. The diagonalization language Ld , on the other hand, is not RE. As a result, our assumption that Lu is recursive is incorrect (not RE means not recursive). As a result, we can argue Lu is RE but not recursive. The following graphic depicts the creation of M for Ld :
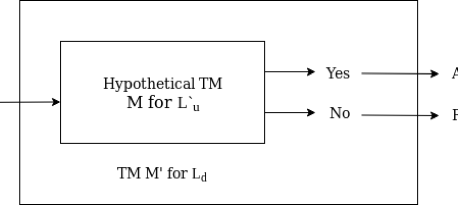
Fig 7: Construction of M’ for Ld
Key takeaway
If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable. There is no technique for determining the answer to an undecidable problem for a given input.
A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing- Acceptable.
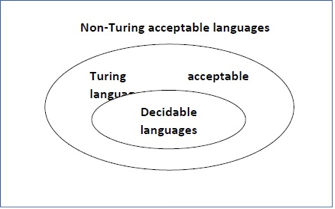
Fig 8: Decidable language
A decision downside P is decidable if the language L of all affirmative instances to P is decidable.
For a decidable language, for every input string, the thulium halts either at the settle for or the reject state as pictured within the following diagram -
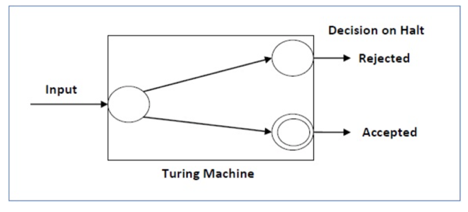
Fig 9: Shows different state
Example 1
Find out whether or not the subsequent downside is decidable or not − Is a range ‘m’ prime?
Solution
Prime numbers =
Divide the amount ‘m’ by all the numbers between ‘2’ and ‘√m’ ranging from ‘2’.
If any of those numbers turn out a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the solution may well be created by ‘Yes’ or ‘No’.
Hence, it’s a decidable downside.
Example 2
Given an everyday language L and string w, however will we have a tendency to
Check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted
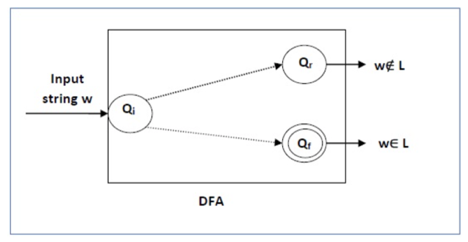
Fig 10: DFA diagram
Some additional decidable issues are -
• Does DFA settle for the empty language?
• Is L1 ∩ L2 = ∅ for normal sets?
Key takeaway:
● If a language L is decidable, then its complement L’ is additionally decidable
● If a language is decidable, then there’s AN functionary for it.
It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1, x 2, x 3 ,………, x n )
N = (y 1, y 2, y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1, i 2……… i k,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 ……. y ik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x2 x1 x3 = ‘aaabbaaa’
And y2 y1 y3 = ‘aaabbaaa’
We can see that
x2 x1 x3 = y2 y1 y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 3
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post
Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Ab | Bab | Bbaaa |
N | a | Ba | Bab |
In this case, there is no solution because −
| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.
Total recursive function -
If f(a1, a2, ...an) is defined for all its arguments, a recursive function is called the complete recursive function. Let f(a1, a2, ...an) be a function defined for function g(b1, b2, ...bn). If each element of f is assigned to a unique element of function g, then f is a total function.
● A complete function is called recursive or primitive recursive if and only if it is an initial over-n function, or if it is obtained by applying a finite number of times composition or recursion to an initial over-n function.
● A complete recursive function or primitive recursive function is the multiplication of two positive integers.
● Not all complete recursive functions are recursive primitive functions.
● The function of Ackerman is a complete function.
● Both primitive recursive features are complete functions.
Partial recursive function -
A function f(a1, a2,....an) determined by a TM is referred to as a partial recursive function. If f is defined for some but not all values of a1, a2,....an. Let f(a1, a2,...an) be a function defined by function g(b1, b2,....bn), then f is a partial function if almost one element of function g is assigned to some element of f.
If it is an initial function over N, a partial function is recursive, or if it is obtained by applying recursion or composition or minimization to an initial function over N.
● The partial recursive function is the subtraction of two positive integers.
● The partial function composition yields a partial(total) function.
● A partial recursive function is the minimization of a complete recursive function.
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory. All primitive recursive functions are total and computable, however not all total computable functions are primitive recursive, as the Ackermann function demonstrates.
It's a function having two arguments, each of which can take any non-negative number as an argument.
Ackermann function is defined as:
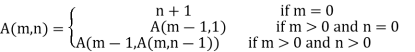
Where m and n are non-negative integers
Ackermann algorithm:
Ackermann(m, n)
{next and goal are arrays indexed from 0 to m, initialized so that next[O]
Through next[m] are 0, goal[O] through goal[m - l] are 1, and goal[m] is -1}
Repeat
Value <-- next[O] + 1
Transferring <-- true
Current <-- O
While transferring do begin
If next[current] = goal[current] then goal[current] <-- value
Else transferring <-- false
Next[current] <-- next[current]+l
Current <-- current + 1
End while
Until next[m] = n + 1
Return value {the value of A(m, n)}
End Ackermann
Here's how the given Algorithm is explained:
Let's look at an example of the algorithm, A(1, 2), where m = 1 and n = 2.
The initial values of next, goal, value, and current, according to the algorithm, are:

Because next[current]!= goal[current], the else statement will be executed, resulting in the transfer being false.
As a result, the following are the values of next, aim, value, and current:

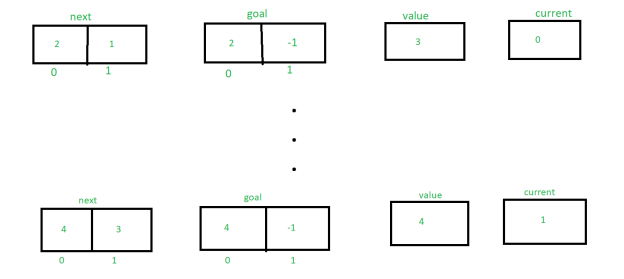
Similarly, tracing the procedure until next[m] = 3 changes the value of next, target, value, and current. The following is an explanation of how the values are changing:


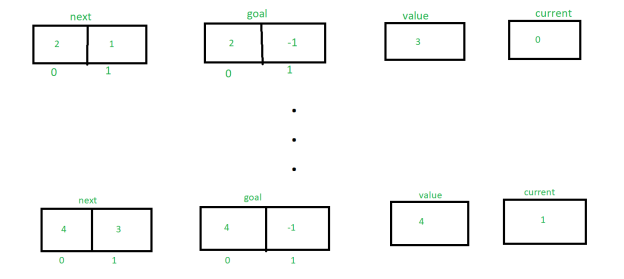
Finally returning the value e.g 4
Analysis of this algorithm:
The time complexity of this algorithm is: O(mA(m, n)) to compute A(m, n).
The space complexity of this algorithm is: O(m) to compute A(m, n).
Key takeaway
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45 and Computation”, Addison-Wesley,ISBN
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454
Unit - 5
Turing Machine
An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
Formal definition
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ : alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of turing machine
With the help of the following representation, the turning machine can be modeled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.
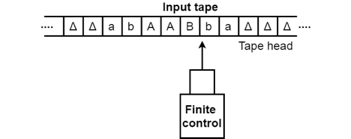
Fig 2: Basic model of TM
Various features of the Turing machine exist:
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
It consists of a head that reads the input tape.
A state register stores the state of the information processing system.
Even though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements.
Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.
Example: Creating a turing machine which accepts the language of aba over ∑ = {a, b}
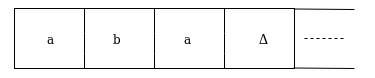
Sol: We'll think that the string 'aba' is positioned like this on the input tape:
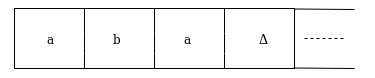
The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop.
Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:
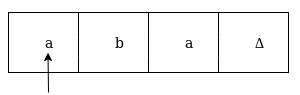
The next move are δ(q0, a) = δ(q1, A, R) which means it goes to state q1, replaced by A and head moves toward right :
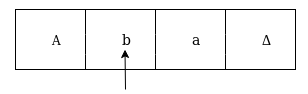
The next move are δ(q1, b) = δ(q2, B, R) which means it goes to state q2 , replaced by B and head moves toward right :
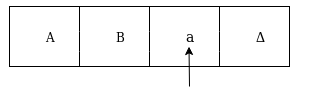
The next move are δ(q2, a) = δ(q3, A, R) which means it goes to state q3 , replaced by A and head moves toward right :
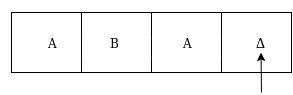
The move δ(q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine .
State | a | b | ᇫ |
q0 | (q1, A, R) | - | - |
q1 | - | (q2,B,R) | - |
q2 | (q3,A,R) | - | - |
q3 | - | - | (q4, ᇫ , S) |
q4 | - | - | - |
The turing machine can be represented by transition diagram –
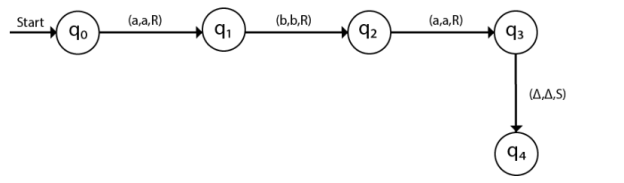
Fig 3: Transition diagram for turing machine
As a transducer, a Turing machine can be employed. The most apparent method to do this is to treat the full nonblank area of the first cassette as input, and the complete non blank piece of the second tape as output when the machine halts.
In other words, a Turing machine defines a function y=f(x) for strings x, y is a member of Σ * if
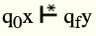
Where qf is a final state.
If a Turing machine can execute the given task, then a function f is Turing computable.
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, method of infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
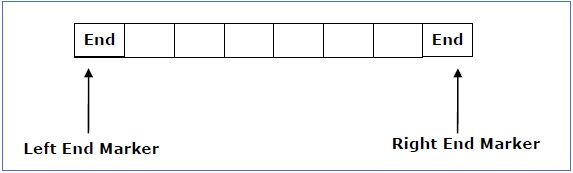
Fig 4: Linear bounded automata
The measurement is limited to the region bounded by constants.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.
Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.
δ(non-halting-state, symbol) = UNDEF
By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission
δ(R,σ) = (R,σ) ∀ σ ∈ Σ
Simply send a missing transition to this state without tape modification with this addition, i.e.,
δ(non-halting-state, symbol) = (R, symbol)
The easiest computer we can create that runs indefinitely is this:
RunForever = ( {s,h}, Σ, {}, s, {h} )
There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"
● Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
● Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
● Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Recursive language (RE) –
A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’. The computing device can halt on every occasion and provides associate answer (accepted or rejected) for every and each string input. A language ‘L’ is decidable if it’s a algorithmic language. All decidable languages area unit algorithmic languages and vice-versa.
Recursively countable language (RCE) –
A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.
By definition, all REC languages {are also|also area unit|are} RE languages however not all RE languages are REC languages.
A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing-Acceptable.
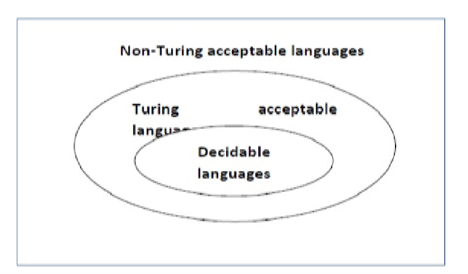
Fig 5: Each decidable language is Turing-Acceptable.
A decision downside P is decidable if the language L of all affirmative instances to P is decidable.
For a decidable language, for every input string, the thulium halts either at the settle for or the reject state as pictured within the following diagram –
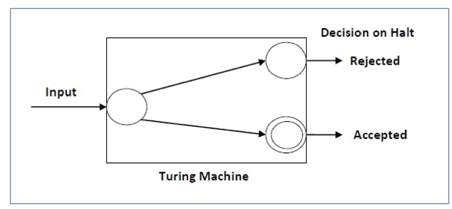
Fig 6: Turing machine
Key takeaway
A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’.
A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.
If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable. There is no technique for determining the answer to an undecidable problem for a given input.
We frequently come across similar situations in the theory of computation where the answer is either 'yes' or 'no.' Solvable or decidable problems are those that can be answered with a yes or no. Otherwise, the problem category is referred to as unsolvable or undecidable.
Example
Ambiguity of context-free languages: There is no Turing machine that, given a context-free language, will always halt in a finite amount of time and say whether the language is ambiguous or not.
Equivalence of two context-free languages: There is no Turing computer that, given two context-free languages, will always halt in a finite amount of time and say whether the languages are equal or not.
Everything or completeness of CFG: It is unclear whether CFG will generate all possible strings of input alphabet (*) given a CFG and input alphabet.
Regularity of CFL, CSL, REC and REC: It's impossible to say whether a CFL, CSL, REC, or REC is regular given a CFL, CSL, REC, or REC.
Undecidability of Universal Languages:
The universal communication system We must show that Lu is undecidable because it is a recursively enumerable language (non-recursive).
Theorem - Lu is a recursive but not a recursive RE.
Proof - Consider the fact that the language Lu is recursively enumerable. Lu will be assumed to be recursive. The complement of Lu, which is Lu, is recursive as well. We can, however, construct a TM Ld if we have a TM M that accepts Lu. The diagonalization language Ld , on the other hand, is not RE. As a result, our assumption that Lu is recursive is incorrect (not RE means not recursive). As a result, we can argue Lu is RE but not recursive. The following graphic depicts the creation of M for Ld :
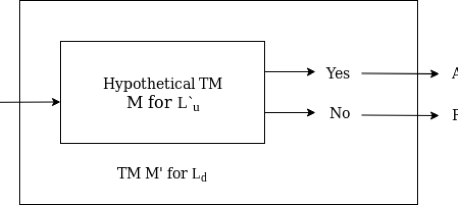
Fig 7: Construction of M’ for Ld
Key takeaway
If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable. There is no technique for determining the answer to an undecidable problem for a given input.
A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing- Acceptable.
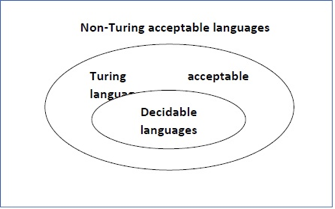
Fig 8: Decidable language
A decision downside P is decidable if the language L of all affirmative instances to P is decidable.
For a decidable language, for every input string, the thulium halts either at the settle for or the reject state as pictured within the following diagram -
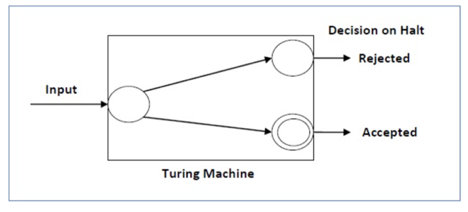
Fig 9: Shows different state
Example 1
Find out whether or not the subsequent downside is decidable or not − Is a range ‘m’ prime?
Solution
Prime numbers =
Divide the amount ‘m’ by all the numbers between ‘2’ and ‘√m’ ranging from ‘2’.
If any of those numbers turn out a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the solution may well be created by ‘Yes’ or ‘No’.
Hence, it’s a decidable downside.
Example 2
Given an everyday language L and string w, however will we have a tendency to
Check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted
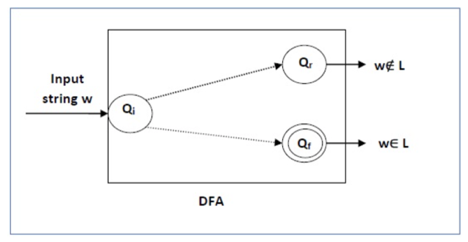
Fig 10: DFA diagram
Some additional decidable issues are -
• Does DFA settle for the empty language?
• Is L1 ∩ L2 = ∅ for normal sets?
Key takeaway:
● If a language L is decidable, then its complement L’ is additionally decidable
● If a language is decidable, then there’s AN functionary for it.
It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1, x 2, x 3 ,………, x n )
N = (y 1, y 2, y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1, i 2……… i k,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 ……. y ik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x2 x1 x3 = ‘aaabbaaa’
And y2 y1 y3 = ‘aaabbaaa’
We can see that
x2 x1 x3 = y2 y1 y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 3
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post
Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Ab | Bab | Bbaaa |
N | a | Ba | Bab |
In this case, there is no solution because −
| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.
Total recursive function -
If f(a1, a2, ...an) is defined for all its arguments, a recursive function is called the complete recursive function. Let f(a1, a2, ...an) be a function defined for function g(b1, b2, ...bn). If each element of f is assigned to a unique element of function g, then f is a total function.
● A complete function is called recursive or primitive recursive if and only if it is an initial over-n function, or if it is obtained by applying a finite number of times composition or recursion to an initial over-n function.
● A complete recursive function or primitive recursive function is the multiplication of two positive integers.
● Not all complete recursive functions are recursive primitive functions.
● The function of Ackerman is a complete function.
● Both primitive recursive features are complete functions.
Partial recursive function -
A function f(a1, a2,....an) determined by a TM is referred to as a partial recursive function. If f is defined for some but not all values of a1, a2,....an. Let f(a1, a2,...an) be a function defined by function g(b1, b2,....bn), then f is a partial function if almost one element of function g is assigned to some element of f.
If it is an initial function over N, a partial function is recursive, or if it is obtained by applying recursion or composition or minimization to an initial function over N.
● The partial recursive function is the subtraction of two positive integers.
● The partial function composition yields a partial(total) function.
● A partial recursive function is the minimization of a complete recursive function.
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory. All primitive recursive functions are total and computable, however not all total computable functions are primitive recursive, as the Ackermann function demonstrates.
It's a function having two arguments, each of which can take any non-negative number as an argument.
Ackermann function is defined as:
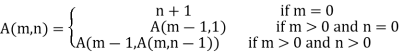
Where m and n are non-negative integers
Ackermann algorithm:
Ackermann(m, n)
{next and goal are arrays indexed from 0 to m, initialized so that next[O]
Through next[m] are 0, goal[O] through goal[m - l] are 1, and goal[m] is -1}
Repeat
Value <-- next[O] + 1
Transferring <-- true
Current <-- O
While transferring do begin
If next[current] = goal[current] then goal[current] <-- value
Else transferring <-- false
Next[current] <-- next[current]+l
Current <-- current + 1
End while
Until next[m] = n + 1
Return value {the value of A(m, n)}
End Ackermann
Here's how the given Algorithm is explained:
Let's look at an example of the algorithm, A(1, 2), where m = 1 and n = 2.
The initial values of next, goal, value, and current, according to the algorithm, are:

Because next[current]!= goal[current], the else statement will be executed, resulting in the transfer being false.
As a result, the following are the values of next, aim, value, and current:

Similarly, tracing the procedure until next[m] = 3 changes the value of next, target, value, and current. The following is an explanation of how the values are changing:


Finally returning the value e.g 4
Analysis of this algorithm:
The time complexity of this algorithm is: O(mA(m, n)) to compute A(m, n).
The space complexity of this algorithm is: O(m) to compute A(m, n).
Key takeaway
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45 and Computation”, Addison-Wesley,ISBN
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454
Unit - 5
Turing Machine
An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
Formal definition
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ : alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of turing machine
With the help of the following representation, the turning machine can be modeled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.
Fig 2: Basic model of TM
Various features of the Turing machine exist:
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
It consists of a head that reads the input tape.
A state register stores the state of the information processing system.
Even though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements.
Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.
Example: Creating a turing machine which accepts the language of aba over ∑ = {a, b}
Sol: We'll think that the string 'aba' is positioned like this on the input tape:
The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop.
Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:
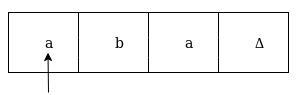
The next move are δ(q0, a) = δ(q1, A, R) which means it goes to state q1, replaced by A and head moves toward right :
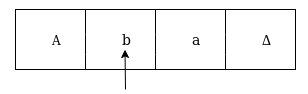
The next move are δ(q1, b) = δ(q2, B, R) which means it goes to state q2 , replaced by B and head moves toward right :
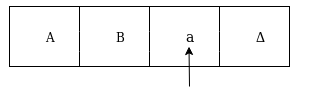
The next move are δ(q2, a) = δ(q3, A, R) which means it goes to state q3 , replaced by A and head moves toward right :
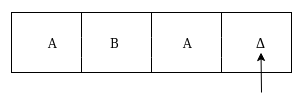
The move δ(q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine .
State | a | b | ᇫ |
q0 | (q1, A, R) | - | - |
q1 | - | (q2,B,R) | - |
q2 | (q3,A,R) | - | - |
q3 | - | - | (q4, ᇫ , S) |
q4 | - | - | - |
The turing machine can be represented by transition diagram –
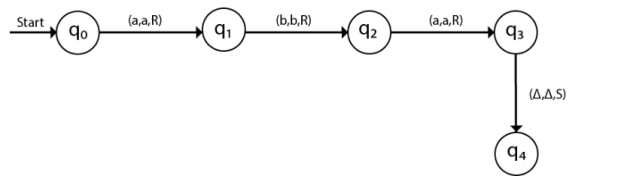
Fig 3: Transition diagram for turing machine
As a transducer, a Turing machine can be employed. The most apparent method to do this is to treat the full nonblank area of the first cassette as input, and the complete non blank piece of the second tape as output when the machine halts.
In other words, a Turing machine defines a function y=f(x) for strings x, y is a member of Σ * if
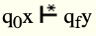
Where qf is a final state.
If a Turing machine can execute the given task, then a function f is Turing computable.
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, method of infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
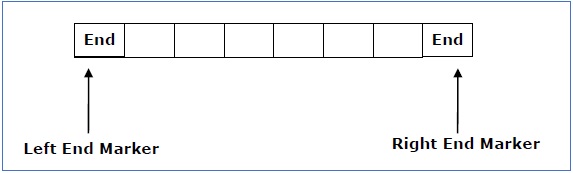
Fig 4: Linear bounded automata
The measurement is limited to the region bounded by constants.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.
Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.
δ(non-halting-state, symbol) = UNDEF
By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission
δ(R,σ) = (R,σ) ∀ σ ∈ Σ
Simply send a missing transition to this state without tape modification with this addition, i.e.,
δ(non-halting-state, symbol) = (R, symbol)
The easiest computer we can create that runs indefinitely is this:
RunForever = ( {s,h}, Σ, {}, s, {h} )
There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"
● Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
● Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
● Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Unit - 5
Turing Machine
An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
Formal definition
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ : alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of turing machine
With the help of the following representation, the turning machine can be modeled.
- The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.
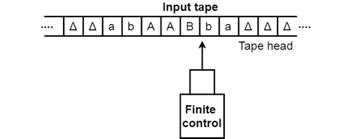
Fig 2: Basic model of TM
Various features of the Turing machine exist:
● It has an external memory that recalls an arbitrary, long input list.
● It has infinite capability for memory.
● The model has a method in which it is easy to read the input on the tape on the left or right.
● Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
It consists of a head that reads the input tape.
A state register stores the state of the information processing system.
Even though they are recursively enumerable, the Turing machine embraces all the language. Recursive implies repeating for any number of times the same set of rules, and enumerable means a collection of elements.
Computable attributes, such as addition, multiplication, subtraction, division, power function, and many more are also accepted by the TM.
Example: Creating a turing machine which accepts the language of aba over ∑ = {a, b}
Sol: We'll think that the string 'aba' is positioned like this on the input tape:
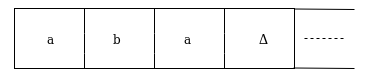
The tape head reads the sequence up to the Δ characters. If the tape head is read 'aba' string, then after reading, TM will stop.
Now we're going to see how this turbo machine is going to work for aba. The condition is originally q0 and the head points to an as:
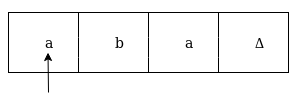
The next move are δ(q0, a) = δ(q1, A, R) which means it goes to state q1, replaced by A and head moves toward right :
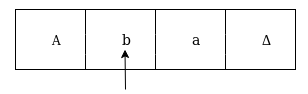
The next move are δ(q1, b) = δ(q2, B, R) which means it goes to state q2 , replaced by B and head moves toward right :
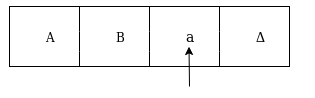
The next move are δ(q2, a) = δ(q3, A, R) which means it goes to state q3 , replaced by A and head moves toward right :
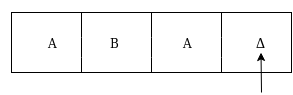
The move δ(q3, Δ) = (q4, Δ, S) therefore, it will go to state q4 which is the HALT state and HALT state is always an accept state for any Turing Machine .
State | a | b | ᇫ |
q0 | (q1, A, R) | - | - |
q1 | - | (q2,B,R) | - |
q2 | (q3,A,R) | - | - |
q3 | - | - | (q4, ᇫ , S) |
q4 | - | - | - |
The turing machine can be represented by transition diagram –
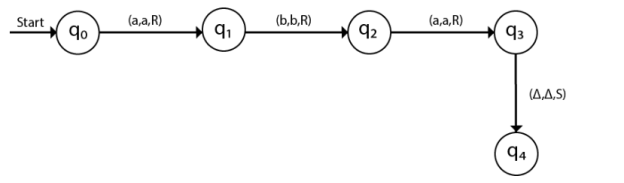
Fig 3: Transition diagram for turing machine
As a transducer, a Turing machine can be employed. The most apparent method to do this is to treat the full nonblank area of the first cassette as input, and the complete non blank piece of the second tape as output when the machine halts.
In other words, a Turing machine defines a function y=f(x) for strings x, y is a member of Σ * if
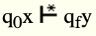
Where qf is a final state.
If a Turing machine can execute the given task, then a function f is Turing computable.
1. Multiple tracks Alan Turing Machine:
● A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head
That reads and writes all of them one by one.
● A k-track information processing system may be simulated by one track information processing system.
2. Two-way infinite Tape Alan Turing Machine:
● Infinite tape of two-way infinite tape information processing system is
Boundless in each direction left and right.
● Two-way infinite tape information processing system may be simulated by
Unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison
Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
● It has multiple tapes and is controlled by one head.
● The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.
● Multi-tape information processing system may be simulated by a single-tap information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
● The multi-tape information processing system has multiple tapes and multiple Heads.
● Each tape is controlled by a separate head.
● Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.
5. Multi-dimensional Tape Alan Turing Machine:
● It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.
● Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
● A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.
● In one step all the heads sense the scanned symbols and move or write severally.
● Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
● A non-deterministic information processing system encompasses a single, method of infinite tape.
● For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.
● A non-deterministic information processing system is an adored settled information processing system.
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automata can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
● Q is a finite set of states
● X is the tape alphabet
● ∑ is the input alphabet
● q0 is the initial state
● ML is the left end marker
● MR is the right end marker where MR ≠ ML
● δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
● F is the set of final states.
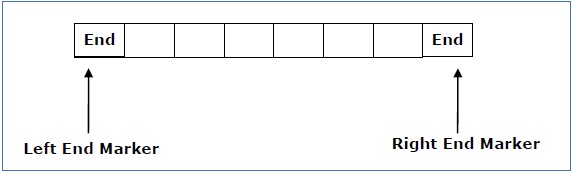
Fig 4: Linear bounded automata
The measurement is limited to the region bounded by constants.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.
Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.
δ(non-halting-state, symbol) = UNDEF
By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission
δ(R,σ) = (R,σ) ∀ σ ∈ Σ
Simply send a missing transition to this state without tape modification with this addition, i.e.,
δ(non-halting-state, symbol) = (R, symbol)
The easiest computer we can create that runs indefinitely is this:
RunForever = ( {s,h}, Σ, {}, s, {h} )
There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"
● Union and Intersection
Recursive
L1 x L2 and L1 x L2 are both recursive if L1 is recursive and L2 is recursive.
Using a multitape TM:
● Copy to Tape 2 and Tape 3 inputs
● Run M1 to tape 2 and M2 to tape 3 (neither will run forever; i.e.we get a result)
● They will determine whether x is in L1 and/or L2
● Test if approved by both M1 and M2 (intersection)
● Test if one is approved by M1 and M2 (union)
If L1 and L2 are recursive, the difference between L1 - L2=L1 and L2 is recursive.
Recursively Enumerable
If L1 and L2 are enumerated recursively, then L1 ∪ L2 and L1 ∩ L2 are recursively enumerated .
● Similar to the recursive case, but the case where M1 and M2 will run constantly
● Simulate simultaneously running M1 and M2-alternate one move from each machine.
A union, for reference,
● If any computer ever accepts it, accept it.
● If any machine ever refuses or fails, then the other machine continues to run.
If L is enumerated recursively and L is enumerated recursively, L is enumerated recursively.
● Let M and M be TMs, respectively, that accept L and L.
● Simultaneously, Run M and M'
● It must be agreed for any term x by any one of M or M'
● Therefore, either M or M 'will stop and agree
● If M stops and agrees, then stop and embrace.
● If M' stops and embraces, then stop and deny.
The TM that runs M and M at the same time always stops and accepts or refuses so that L and L are recursive.
If L is enumerable recursively, and L is not recursive, then L is not enumerable recursively.
● Concatenation
If L1 and L2 are two recursive languages, the L1.L2 concatenation would also be recursive. For instance:
L1 = {anbncn|n>=0}
L2 = {dmemfm|m>=0}
L3 = L1.L2
= {anbncndn emfm|m>=0 and n>=0} is also recursive.
L1 states that n no. Of a's is followed by n no. Of b's, and n no. Of c's. L2 says that m no. Of d's is followed by m no. Of e's, m no. Of f's. First, their concatenation matches no. Of a's, b's, and c's, then no. Of d's, e's, and f's. It can therefore be determined by TM.
● Kleene Closure
If L1 is recursive, its L1* smaller closure would also be recursive. For instance:
L1 = {anbncn|n>=0}
L1*= { anbncn||n>=0}* is also recursive.
Recursive language (RE) –
A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’. The computing device can halt on every occasion and provides associate answer (accepted or rejected) for every and each string input. A language ‘L’ is decidable if it’s a algorithmic language. All decidable languages area unit algorithmic languages and vice-versa.
Recursively countable language (RCE) –
A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.
By definition, all REC languages {are also|also area unit|are} RE languages however not all RE languages are REC languages.
A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing-Acceptable.
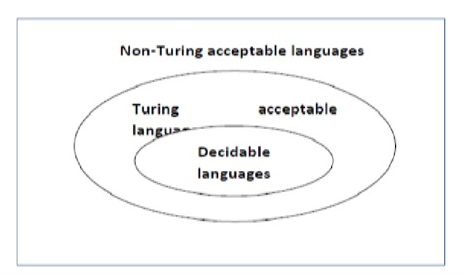
Fig 5: Each decidable language is Turing-Acceptable.
A decision downside P is decidable if the language L of all affirmative instances to P is decidable.
For a decidable language, for every input string, the thulium halts either at the settle for or the reject state as pictured within the following diagram –
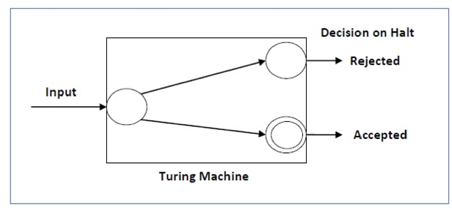
Fig 6: Turing machine
Key takeaway
A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’.
A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren’t in ‘L’.
If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable. There is no technique for determining the answer to an undecidable problem for a given input.
We frequently come across similar situations in the theory of computation where the answer is either 'yes' or 'no.' Solvable or decidable problems are those that can be answered with a yes or no. Otherwise, the problem category is referred to as unsolvable or undecidable.
Example
Ambiguity of context-free languages: There is no Turing machine that, given a context-free language, will always halt in a finite amount of time and say whether the language is ambiguous or not.
Equivalence of two context-free languages: There is no Turing computer that, given two context-free languages, will always halt in a finite amount of time and say whether the languages are equal or not.
Everything or completeness of CFG: It is unclear whether CFG will generate all possible strings of input alphabet (*) given a CFG and input alphabet.
Regularity of CFL, CSL, REC and REC: It's impossible to say whether a CFL, CSL, REC, or REC is regular given a CFL, CSL, REC, or REC.
Undecidability of Universal Languages:
The universal communication system We must show that Lu is undecidable because it is a recursively enumerable language (non-recursive).
Theorem - Lu is a recursive but not a recursive RE.
Proof - Consider the fact that the language Lu is recursively enumerable. Lu will be assumed to be recursive. The complement of Lu, which is Lu, is recursive as well. We can, however, construct a TM Ld if we have a TM M that accepts Lu. The diagonalization language Ld , on the other hand, is not RE. As a result, our assumption that Lu is recursive is incorrect (not RE means not recursive). As a result, we can argue Lu is RE but not recursive. The following graphic depicts the creation of M for Ld :
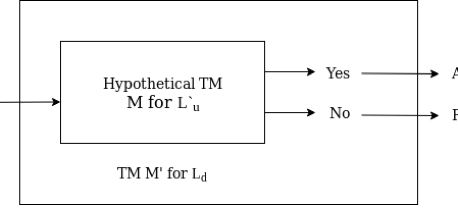
Fig 7: Construction of M’ for Ld
Key takeaway
If there is no Turing machine that will always cease in a finite amount of time to deliver a yes or no answer, the problem is undecidable. There is no technique for determining the answer to an undecidable problem for a given input.
A language is termed Decidable or algorithmic if there’s a data processor that accepts and halts on each input string w. Each decidable language is Turing- Acceptable.
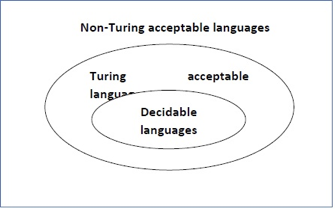
Fig 8: Decidable language
A decision downside P is decidable if the language L of all affirmative instances to P is decidable.
For a decidable language, for every input string, the thulium halts either at the settle for or the reject state as pictured within the following diagram -
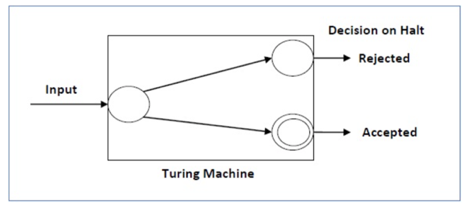
Fig 9: Shows different state
Example 1
Find out whether or not the subsequent downside is decidable or not − Is a range ‘m’ prime?
Solution
Prime numbers =
Divide the amount ‘m’ by all the numbers between ‘2’ and ‘√m’ ranging from ‘2’.
If any of those numbers turn out a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the solution may well be created by ‘Yes’ or ‘No’.
Hence, it’s a decidable downside.
Example 2
Given an everyday language L and string w, however will we have a tendency to
Check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted
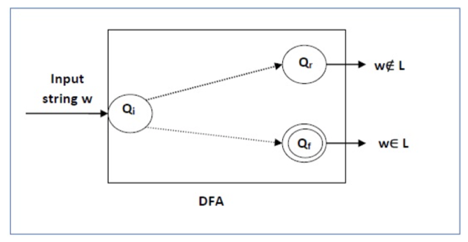
Fig 10: DFA diagram
Some additional decidable issues are -
• Does DFA settle for the empty language?
• Is L1 ∩ L2 = ∅ for normal sets?
Key takeaway:
● If a language L is decidable, then its complement L’ is additionally decidable
● If a language is decidable, then there’s AN functionary for it.
It was introduced by Emil Post and is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x 1, x 2, x 3 ,………, x n )
N = (y 1, y 2, y 3 ,………, y n )
We can say that there is a Post Correspondence Solution, if for some i 1, i 2……… i k,
Where 1 ≤ i j ≤ n, the condition x i1 …….x ik = y i1 ……. y ik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
Have a Post Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Abb | Aa | Aaa |
N | Bba | Aaa | Aa |
Here,
x2 x1 x3 = ‘aaabbaaa’
And y2 y1 y3 = ‘aaabbaaa’
We can see that
x2 x1 x3 = y2 y1 y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 3
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post
Correspondence Solution?
Sol:
| X1 | X2 | X3 |
M | Ab | Bab | Bbaaa |
N | a | Ba | Bab |
In this case, there is no solution because −
| x 2 x 1 x 3 | ≠ | y 2 y 1 y 3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.
Total recursive function -
If f(a1, a2, ...an) is defined for all its arguments, a recursive function is called the complete recursive function. Let f(a1, a2, ...an) be a function defined for function g(b1, b2, ...bn). If each element of f is assigned to a unique element of function g, then f is a total function.
● A complete function is called recursive or primitive recursive if and only if it is an initial over-n function, or if it is obtained by applying a finite number of times composition or recursion to an initial over-n function.
● A complete recursive function or primitive recursive function is the multiplication of two positive integers.
● Not all complete recursive functions are recursive primitive functions.
● The function of Ackerman is a complete function.
● Both primitive recursive features are complete functions.
Partial recursive function -
A function f(a1, a2,....an) determined by a TM is referred to as a partial recursive function. If f is defined for some but not all values of a1, a2,....an. Let f(a1, a2,...an) be a function defined by function g(b1, b2,....bn), then f is a partial function if almost one element of function g is assigned to some element of f.
If it is an initial function over N, a partial function is recursive, or if it is obtained by applying recursion or composition or minimization to an initial function over N.
● The partial recursive function is the subtraction of two positive integers.
● The partial function composition yields a partial(total) function.
● A partial recursive function is the minimization of a complete recursive function.
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory. All primitive recursive functions are total and computable, however not all total computable functions are primitive recursive, as the Ackermann function demonstrates.
It's a function having two arguments, each of which can take any non-negative number as an argument.
Ackermann function is defined as:
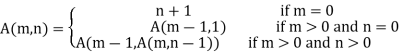
Where m and n are non-negative integers
Ackermann algorithm:
Ackermann(m, n)
{next and goal are arrays indexed from 0 to m, initialized so that next[O]
Through next[m] are 0, goal[O] through goal[m - l] are 1, and goal[m] is -1}
Repeat
Value <-- next[O] + 1
Transferring <-- true
Current <-- O
While transferring do begin
If next[current] = goal[current] then goal[current] <-- value
Else transferring <-- false
Next[current] <-- next[current]+l
Current <-- current + 1
End while
Until next[m] = n + 1
Return value {the value of A(m, n)}
End Ackermann
Here's how the given Algorithm is explained:
Let's look at an example of the algorithm, A(1, 2), where m = 1 and n = 2.
The initial values of next, goal, value, and current, according to the algorithm, are:

Because next[current]!= goal[current], the else statement will be executed, resulting in the transfer being false.
As a result, the following are the values of next, aim, value, and current:

Similarly, tracing the procedure until next[m] = 3 changes the value of next, target, value, and current. The following is an explanation of how the values are changing:


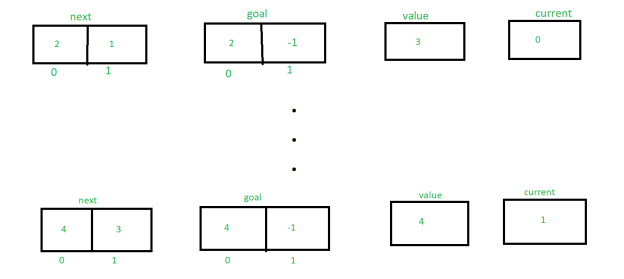
Finally returning the value e.g 4
Analysis of this algorithm:
The time complexity of this algorithm is: O(mA(m, n)) to compute A(m, n).
The space complexity of this algorithm is: O(m) to compute A(m, n).
Key takeaway
The Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest examples of a complete computable function that is not basic recursive in computability theory.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGrawHill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45 and Computation”, Addison-Wesley,ISBN
- Daniel Cohen, “Introduction to Computer Theory”, Wiley & Sons, ISBN 97881265133454