Unit - 1
Finite Automata
Finite Automata(FA) is the simplest pattern recognition machine. The finite automatic or finite state machine is an abstract machine with five components or tuples. It has a set of states and rules that switch from one state to another, but it depends on the input symbol that is added. It is essentially an abstract digital machine model.
Some important features of general automation are shown in the figure below:
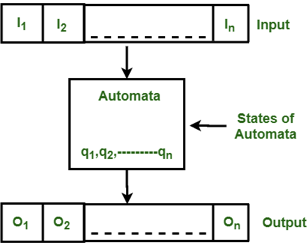
Fig 1: Features of finite automata
The figure above shows the following automated features:
● Input
● Output
● State of automata
● State relation
● Output relation
A Finite Automata consists of the following:
{Q, Σ, q, F, δ}.
Where,
Q: Finite set of states.
Σ: set of Input Symbols.
q: Initial state.
F: set of Final States.
δ: Transition Function.
Finite automata is divided into 2 types:
- Deterministic Finite Automaton (DFA)
In this, for each input symbol, the state to which the machine will move can be determined. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
An automaton can be represented by a 5-tuple (Q, ∑, δ, q 0 , F),
Where −
Q is a finite set of states.
∑ is a finite set of symbols, called the alphabet of the automaton.
δ is the transition function.
q 0 is the initial state from where any input is processed (q 0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
2. Non-deterministic Finite Automaton (NDFA)
In NDFA, the machine can move to any combination of the states. Hence, it is called Non-deterministic Automaton as it has finite number of states.
Q → Finite non-empty set of states.
∑ → Finite non-empty set of input symbols.
∂ → Transitional Function.
q0 → Beginning state.
F → Final State
Basic terminology
Alphabet
● Definition − An alphabet is any finite set of symbols.
● Example − ∑ = {a, b, c, d} is an alphabet set where ‘a’, ‘b’, ‘c’, and ‘d’ are symbols.
String
● Definition − A string is a finite sequence of symbols taken from ∑.
● Example − ‘cabcad’ is a valid string on the alphabet set ∑ = {a, b, c, d}
Languages
● Definition − A language is a subset of ∑* for some alphabet ∑. It can be finite or infinite.
● Example − If the language takes all possible strings of length 2 over ∑ = {a, b}, then
L1 = {ab, aa, ba, bb} finite language
L2 = {a,aa,aaa,abb,abab} infinite language
Key takeaway:
Finite Automata(FA) is the simplest pattern recognition machine.
The finite automatic or finite state machine is an abstract machine with five components or tuples.
In DFA, for each input symbol, the state to which the machine will move can be determined.
In NDFA, the machine can move to any combination of the states.
The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:
- Type 0 known as Unrestricted Grammar.
- Type 1 known as Context Sensitive Grammar.
- Type 2 known as Context Free Grammar.
- Type 3 Regular Grammar.
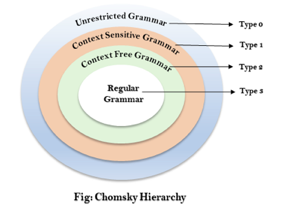
Fig 2: Chomsky hierarchy
The above diagram shows the hierarchy of chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.
● Type 0 grammar -
Type 0 grammar is known as Unrestricted grammar.The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.
Example:
- BAa → aa
- P → p
● Type 1 grammar -
Type 1 grammar is known as Context Sensitive Grammar.Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:
● There may be more than one symbol on the left side of their development rules for context-sensitive grammar.
● The number of left-hand symbols does not surpass the number of right-hand symbols.
● The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.
● The Type 1 grammar should be Type 0. Production is in the form of V →T in type1
Key takeaway:
● Where the number of symbols in V is equal to or less than T
Example:
- S → AT
- T → xy
- A → a
● Type 2 grammar -
Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:
A → α
Key takeaway:
● Where A is any single non-terminal and is any combination of terminals and non-terminals.
Example:
- A → aBb
- A → b
- B → a
● Type 3 grammar -
Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modeled.
Type3 has to be in the form of -
V → T*V / T*
Example:
A → xy
Key takeaway:
● The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.
In this, for each input symbol, the state to which the machine will move can be determined. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
● An automaton can be represented by a 5-tuple (Q, ∑, δ, q 0 , F), where −
● Q is a finite set of states.
● ∑ is a finite set of symbols, called the alphabet of the automaton.
● δ is the transition function.
● q0 is the initial state from where any input is processed (q 0 ∈ Q).
● F is a set of final state/states of Q (F ⊆ Q).
Transition function can be defined as:
δ: Q x ∑→Q
Graphical Representation of DFA
A DFA can be represented by digraphs called state diagram. In which:
- The state is represented by vertices.
- The arc labeled with an input character shows the transitions.
- The initial state is marked with an arrow.
- The final state is denoted by a double circle.
Advantages and disadvantages
● DFAs are used to model a Turing machine.
● They are used as ++ models of computation.
● The union/intersection of the languages recognized by two given DFAs.
● The complement of the language recognized by a given DFA.
Example
Q = {q0, q1, q2}
∑ = {0,1}
q0 = {q0}
F = {q2}
Solution:
Transition Diagram:

Transition Table:
Present State | Next State for Input 0 | Next state of Input 1 |
→q0 | q0 | q1 |
q1 | q2 | q1 |
*q2 | q2 | q2 |
We can now define the notion of acceptance of a string, and thus acceptance of a language, in terms of a DFA.
If ˆδ(q0, x) ∈ F, a string x is said to be accepted by a DFA A = (Q, Σ, δ, q0, F). That is, the DFA will achieve a final state if the string x ∈ Σ ∗ is applied in the initial state.
The language accepted by A is defined as the set of all strings accepted by the DFA A and is denoted by L(A ). That is to say,
L(A ) = {x ∈ Σ* | ˆδ(q0, x) ∈ F}
Example:
Take into account the following DFA:
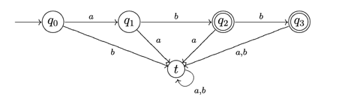
The string ab is the only way to get from the beginning state q0 to the final state q2, and abb is the only way to get to another final state q3. As a result, the DFA's approved language is
{ab, abb}.
Example: Let us recollect the DFA's transition diagram, as given below.

1. It’s important to remember that if the input contains aa, the DFA will take us from the starting state p to the final state r. Due to the fact that r is also a trap state, we will remain at r on any future input.
2. If there is no aa in the input, we will shuffle between p and q but never reach the ultimate state r.
As a result, the DFA accepts the set of all strings over a, b that have aa as a substring, i.e.
{xaay | x, y ∈ {a, b}* }.
In NDFA, the machine can move to any combination of the states. Hence, it is
Called Non-deterministic Automaton.
It has a finite number of states.
● Q → Finite non-empty set of states.
● ∑ → Finite non-empty set of input symbols.
● ∂ → Transitional Function.
● q0 → Beginning state.
● F → Final State
Transition function can be defined as:
δ: Q x ∑ →2Q
Graphical Representation of NFA
An NFA can be represented by digraphs called state diagram. In which:
- The state is represented by vertices.
- The arc labeled with an input character show the transitions.
- The initial state is marked with an arrow.
- The final state is denoted by the double circle.
Example
- Q = {q0, q1, q2}
- ∑ = {0, 1}
- q0 = {q0}
- F = {q2}
Solution:
Transition Diagram:
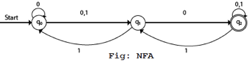
Transition table:
Present State | Next State for Input 0 | Next State of Input 1 |
→q0 | q0, q1 | q1 |
q1 | q2 | q0 |
*q2 | q2 | q1,q2 |
In this figure, we can see that the current state is q0(input 0), and the next state will be q0,q1(input 1) so the next state is q1. When the current state is q1(input 0), the next state will be q2(input 1), the next state is q0. When the current state is q2(input 0), the next state is q2( input 1), the next state will be q1 or q2.
It would seem superficially that deterministic and non-deterministic finite state automata are totally distinct beasts. However, it turns out that they are equivalent. There is a DFA for every language recognized by an NFA that recognizes that language and vice versa.
The NFA to DFA conversion algorithm is relatively simple, even though the resulting DFA is substantially more complicated than the original NFA. I will illustrate this equivalence after the hop and also go through a brief example of converting an NFA to an equivalent DFA.
DFA and NFA Theorem proof -
Let's formally state the theorem we are proving before continuing:
Theorem:
Let the language L ⊆ Σ* be recognized by NFA N = (Σ, Q, q0, F, δ) and assume L.
A DFA D= (Σ, Q ', q'0, F', δ ') exists that also accepts L. (L(N)= L(D)).
We are able to prove by induction that D is equal to N by allowing each state in the DFA D to represent a set of states in the NFA N. Let's define the parameters of D: before we start proofing,
● Q’ is equal to the powerset of Q, Q’ = 2Q
● q’0 = {q0}
● F’ is the set of states in Q’ that contain any element of F, F’ = {q ∈ Q’|q ∩ F ≠ Ø}
● δ’ is the transition function for D. δ’(q,a) = Up∈ q δ(p, a)for q ∈ Q’ and a ∈ Σ
It's worth more explaining, I think δ '. Note that in the set of states Q 'in D, each state is a set of states from Q in N itself. Determine the transition δ (p,a) for each state p in state q in Q 'of D (p is a single state from Q). The union of all δ(q, a) is δ(q,a) .
Now we will demonstrate δ’(q0’, x) =δ’(q0 , x) that for every x i.e L(D) = L (N)
Finite Automata have the following applications:
● A compiler's lexical analysis is designed.
● Regular expressions can be used to recognise the pattern.
● For designing combination and sequential circuits, the Mealy and Moore Machines are used.
● In text editors, it's really useful.
● Spell checkers use this.
NFA with ε-Transition
Epsilon closure for a given state X is a set of states which can be reached from the states X with only (null) or ε moves including the state X itself. In other words, ε - closure for a state can be obtained by union operation of the ε - closure of the states which can be reached from X with a single ε move in a recursive manner.
For the above example ∈ closures are as follows:
∈closure(A): {A, B, C}
∈closure(B): {B, C}
∈closure(C): {C}
Deterministic Finite Automata (DFA): DFA is a finite automata where, for all cases,
When a single input is given to a single state, the machine goes to a single state, i.e., all the moves of the machine can be uniquely determined by the present state and the present input symbol.
Steps to Convert NFA with ε-move to DFA:
Step 1: Take ∈ closure for the beginning state of NFA as beginning state of DFA.
Step 2: Find the states that can be traversed from the present for each input symbol (union of transition value and their closures for each states of NFA present in current state of DFA).
Step 3: If any new state is found, take it as the current state and repeat step 2.
Step 4: Do repeat Step 2 and Step 3 until no new state is present in the DFA transition table.
Step 5: Mark the states of DFA which contain the final state of NFA as final states of DFA.
Transition state table for DFA corresponding to above NFA
States | 0 | 1 |
A,B,C | B,C | A,B,C |
B,C | C | B,C |
C | C | C |
DFA State diagram
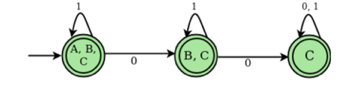
Equivalence of NFA with and without ε-Transition
NFA can be transformed to NFA with ε without ε and NFA without ε can be converted to DFA with ε. We will use a technique to do this that can extract all the ε transformations from the given NFA.
The methods are:
- Find out all the ε transitions from each state from Q. That will be called as ε-closure{q1} where qi ∈ Q.
- Then δ' transitions can be obtained. The δ' transitions mean a ε-closure on δ moves.
- Repeat Step-2 for each input symbol and each state of given NFA.
- Using the resultant states, the transition table for equivalent NFA without ε can be built.
Eliminating Epsilon Transitions
● If epsilon transitions can be eliminated from an FA, then construction of an FA
From a regular expression can be completed.
● Epsilon transitions offers a choice: It allows us to stay in a state or move to a new state, regardless of the input symbol.
● If starting in state s1, state s2 can be reached via a series of epsilon transitions followed by a transition on input symbol x, replacement of the epsilon transitions with a single transition from s1 to s2 on symbol x.
Algorithm for Eliminating Epsilon Transitions
A finite automaton F2 can be build with no epsilon transitions from a finite automaton F1 as follows:
1. The states of F2 are all the states of F1 that have an entering transition labeled by some symbol other than epsilon, plus the start state of F1, which is also the start state of F2.
2. For each state in F1, determine which other states are reachable via epsilon transitions only. If a state of F1 can reach a final state in F1 via epsilon transitions, then the corresponding state is a final state in F2.
For each pair of states i and j in F2, there is a transition from state i to state j on input x if there exists a state k that is reachable from state i via epsilon transitions in F1, and there is a transition in F1 from state k to state j on input x.
Key takeaway -
The computer can switch to any combination of states in the NDFA.
Epsilon closure for a given state X is a set of states that can only be reached with (null) or ε moves from states X, including state X itself.
When the computer is given a single input to a single state, it goes to a single state in DFA.
The term "minimization of DFA" refers to the reduction of the number of states in a particular FA. After reducing the FSM, we have an FSM (finite state machine) with redundant states.
To reduce the DFA, we must follow the various steps. The following are some of them:
Step 1: Using any set of DFA transitions, remove those states that are unreachable from the beginning state.
Step 2: For each pair of states, create a transition table.
Step 3: Divide the transition table into two T1 and T2 tables. T1 is made up of all final states, whereas T2 is made up of non-final states.
Step 4: From T1, find related rows so that:
δ (q, a) = p
δ (r, a) = p
That is, discover the two states with the same a and b values and eliminate one of them.
Step 5: Repeat step 3 until no identical rows in the transition table T1 are available.
Step 6: Carry out steps 3 and 4 for table T2 as well.
Step 7: Now join the T1 and T2 tables that have been decreased. The transition table of reduced DFA is the combined transition table.
Example
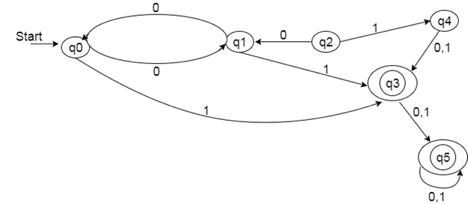
Solution:
Step 1: Remove the inaccessible states q2 and q4 from the provided DFA.
Step 2: Create a transition table for each of the remaining states.
State | 0 | 1 |
→q0 | q1 | q3 |
q1 | q0 | q3 |
*q3 | q5 | q5 |
*q5 | q5 | q5 |
Step 3: Divide the rows of the transition table into two groups as follows:
1. One set consists of rows that begin in non-final states:
State | 0 | 1 |
q0 | q1 | q3 |
q1 | q0 | q3 |
2. A second set has the rows that begin with the final states.
State | 0 | 1 |
q3 | q5 | q5 |
q5 | q5 | q5 |
Step 4: Because there are no identical rows in Set 1, Set 1 will be the same as Set 2.
Step 5: Since q3 and q5 transit to the same state on 0 and 1, row 1 and row 2 in set 2 are comparable. So skip q5 and replace it with q3 in the rest of the questions.
State | 0 | 1 |
q3 | q3 | q3 |
Step 6: Now combine sets 1 and 2 into the following:
State | 0 | 1 |
→q0 | q1 | q3 |
q1 | q0 | q3 |
*q3 | q3 | q3 |
It is now the minimized DFA transition table.
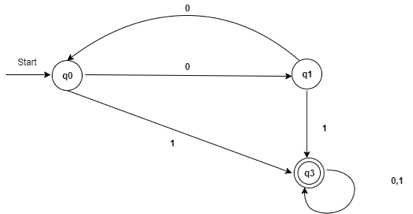
Key takeaway
- The term "minimization of DFA" refers to the reduction of the number of states in a particular FA.
- After reducing the FSM, we have an FSM (finite state machine) with redundant states.
● A Finite Automation has a finite number of states and is also called a Finite State Machine (FSM).
● FA(finite automata) is used for recognition patterns.
● FA have two states, Accept state or Reject state. When the input string is processed successfully, and the automata reaches its final state, then it will accept.
Moore Machine
The Moore machine is a finite state machine in which the current state and the current input symbol define the next state. At a given time, the output symbol depends only on the machine's current state.
Moore machine can be described by 6 tuples (Q, q0, ∑, O, δ, λ) where,
- Q: finite set of states
- q0: initial state of machine
- ∑: finite set of input symbols
- O: output alphabet
- δ: transition function where Q × ∑ → Q
- λ: output function where Q → O
Example:
The state diagram for Moore Machine is-
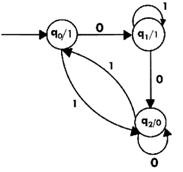
Transition Table for MM(moore machine) is
Current State | Next State(δ) | Output(λ) | |
0 | 1 | ||
q0 | q1 | q2 | 1 |
q1 | q2 | q1 | 1 |
q2 | q2 | q0 | 0 |
Mealy Machine
A Mealy Machine is a machine in which the output symbol depends on the machine's current input symbol and current state. The output is expressed in the Mealy machine with each input symbol for each state, separated by /.
The Mealy machine can be described by 6 tuples (Q, q0, ∑, O, δ, λ') where
- Q: finite set of states
- q0: initial state of machine
- ∑: finite set of input alphabet
- O: output alphabet
- δ: transition function where Q × ∑ → Q
- λ': output function where Q × ∑ →O
Equivalence of moore and merely
Moore and the mealy machine appear differently from each other.
Designing a moore machine with a mealy machine is often possible.
Designing a mealy machine with a moore machine is often possible.
It is possible to transform any Moore machine into a mealy machine.
Moore machine or mealy machine may be used to describe each standard language.
All languages specified by a mealy machine or moore machine are standard.
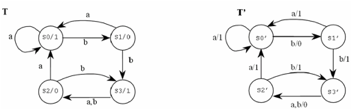
Fig 3: Example of equivalent moore and mealy machine
A moore machine M can never be correctly equal to a mealy machine M 'since one greater than that of the mealy machine M' on the same input is the length of the output string of a moore machine M.
We can, however, overlook the reaction of the moore machine to input λ and say
For all inputs w, moore machine M and a mealy machine M 'are equivalent if
Where b for its initial state is the output of the Moore machine M
Theorem: If M1= (Q, Σ, Δ, δ, λ ,q0 ) is a moore machine then there is an M2 equivalent to M1 mealy machine.
Proof: Create a mealy machine M2 as (Q, Σ, Δ, δ, λ’ ,q0 )
λ’ is describe as-
λ’(q,a) = λ(δ (q,a)) For q and input symbols of all states a
Moore machine is on input 1010 output
0 1 2 2 1
Although the output from the mealy machine constructed is
1 2 2 1
By the equivalence state
In the beginning of output of mealy machine, we can add output of q0 0 of moore machine
The machine generated is therefore equivalent to the Moore machine defined.
Key takeaway -
- In Finite automata there are a finite number of state , which is used for pattern recognition.
- FA (finite automata ) has a two state - Accept or Reject state
- In Moore machine the next state is determined by the present state and current input symbol.
- In Mealy machine the output is represented with each input symbol for each state, separated by /.
References:
- John E. Hopcroft, Rajeev Motwani, Jeffrey D.Ullman, “Introduction to Automata Theory Languages and Computation”, Addison-Wesley,ISBN 0-201-44124-1
- Sanjeev Arora and Boaz Barak, “Computational Complexity: A Modern Approach”,
- Cambridge University Press, ISBN: 0521424267 97805214242643
- John Martin, “Introduction to Languages and The Theory of Computation”, 2nd Edition, McGraw Hill Education, ISBN-13: 978-1-25-900558-9, ISBN-10: 1-25-900558-5
- J.Carroll & D Long, “Theory of Finite Automata”, Prentice Hall, ISBN 0-13-913708-45