UNIT 1
Wave nature of particles and the Schrodinger equation
Electromagnetic waves:
• Electromagnetic waves or EM waves are waves that are created as a result of vibrations between an electric field and a magnetic field.
• When the electric field comes in contact with magnetic field electromagnetic waves are formed, they are known as ‘electromagnetic’ waves.
• The electric field and magnetic field of an electromagnetic wave are perpendicular to each other. They are perpendicular to the direction of the EM wave.
• These waves travel with a constant velocity of 3.00 x 108 m/s in vacuum. They are deflected neither by the electric field, nor magnetic field. They are capable of showing interference or diffraction.
• An electromagnetic wave can travel through air, solid material or vacuum. It does not need a medium to propagate or travel from one place to another.
• Mechanical waves need a medium to travel. EM waves are 'transverse' waves. This means that they are measured by their amplitude and wavelength.

Fig 1. Electromagnetic wave
Properties of EM Waves:
- All the electromagnetic waves travel at the same speed through empty space. The speed is called the speed of light.
- Wavelength is defined as the distance between the corresponding points of adjacent waves.
- Wave frequency is the number of waves that pass a fixed point in a given amount of time.
- The energy of electromagnetic waves depends on their frequency. Low frequency waves have little energy. High frequency waves have lot of energy and are potentially harmful.
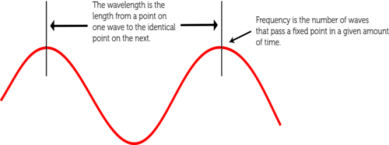
Figure2 – Wavelength
The wave speed is given by
Frequency = Speed / Wave length
Wave length = speed x frequency.
The highest point of a wave is known as 'crest', whereas the lowest point is known as 'trough'.
Electromagnetic spectrum:
The electromagnetic waves are classified and arranged according to their various wavelengths/frequencies; this classification is known as electromagnetic spectrum.
Examples of EM waves are radio waves, microwaves, infrared waves, X-rays, gamma rays.
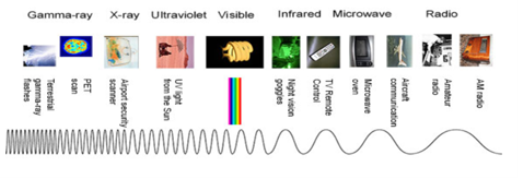
Figure 3. Electromagnetic spectrum
- Electromagnetic spectrum is the distribution of electromagnetic radiation with respect to frequency or wavelength.
- Even though electromagnetic waves travel at the speed of light in a vacuum, they have wide range of frequencies, wavelengths, and photon energies.
- The electromagnetic spectrum comprises the span of all electromagnetic radiation and consists of many subranges, commonly referred to as portions, such as visible light or ultraviolet radiation.
- The various portions carry different names based on differences in behaviour in the emission, transmission, and absorption of the corresponding waves and also based on their different practical applications.
The Time-Independent Schrödinger Equation
The one-dimensional classical wave equation,
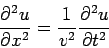 | (1) |
By introducing the separation of variables
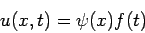 | (2) |
We obtain
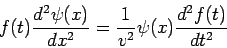 | (3) |
If we introduce one of the standard wave equation solutions for 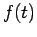 such as
such as 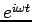 we obtain
we obtain
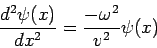 | (4) |
Now we have an ordinary differential equation describing the spatial amplitude of the matter wave as a function of position. The energy of a particle is the sum of kinetic and potential parts
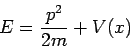 | (5) |
Which can be solved for the momentum, 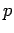 , to obtain
, to obtain
![\begin{displaymath}
p = \{ 2m [ E - V(x) ] \} ^{1/2}
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643161566_496132.png) | (6) |
Now we can use the de Broglie formula to get an expression for the wavelength
![\begin{displaymath}
\lambda = \frac{h}{p} = \frac{h}{\{ 2m [ E - V(x) ] \}^{1/2}}
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643161566_537768.png) | (7) |
The term 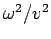 in equation (4) can be rewritten in terms of
in equation (4) can be rewritten in terms of 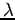 if we recall that
if we recall that 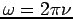 and
and 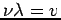 .
.
![\begin{displaymath}
\frac{\omega^2}{v^2} = \frac{4 \pi^2 \nu^2}{v^2} =
\frac{4\pi^2}{\lambda^2} = \frac{2m[E - V(x)]}{\hbar^2}
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643161566_8296008.png) | (8) |
When this result is substituted into equation (4) we obtain the famous time-independent Schrödinger equation
![\begin{displaymath}
\frac{d^2\psi(x)}{dx^2} + \frac{2m}{\hbar^2} [ E - V(x)]\psi(x) = 0
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643161566_9158792.png) | (9) |
Which is almost always written in the form
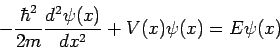 | (10) |
This single-particle one-dimensional equation can easily be extended to the case of three dimensions, where it becomes
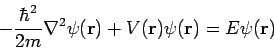 | (11) |
A two-body problem can also be treated by this equation if the mass 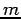 is replaced with a reduced mass
is replaced with a reduced mass  .
.
Time-Dependent Schrödinger Equation
The time-dependent Schrödinger equation cannot be derived using elementary methods and is generally given as a postulate of quantum mechanics.
The single-particle three-dimensional time-dependent Schrödinger equation is
 | (1) |
Where 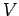 is assumed to be a real function and represents the potential energy of the system.
is assumed to be a real function and represents the potential energy of the system.
Of course, the time-dependent equation can be used to derive the time-independent equation. If we write the wavefunction as a product of spatial and temporal terms, 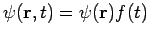 , then equation (1) becomes
, then equation (1) becomes
![\begin{displaymath}
\psi({\bf r}) i \hbar \frac{df(t)}{dt} = f(t) \left[
- \frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643161567_4173183.png) | (2) |
Or
![\begin{displaymath}
\frac{i \hbar}{f(t)} \frac{df}{dt} = \frac{1}{\psi({\bf r})}...
...frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643161567_459181.png) | (3) |
Since the left-hand side is a function of 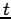 only and the right-hand side is a function of
only and the right-hand side is a function of 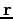 only, the two sides must equal a constant.
only, the two sides must equal a constant.
If we tentatively designate this constant 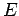 then we extract two ordinary differential equations, namely
then we extract two ordinary differential equations, namely
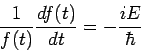 | (4) |
And
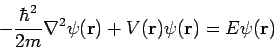 | (5) |
The latter equation is once again the time-independent Schrödinger equation.
Theformer equation is easily solved to yield
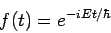 | (6) |
The Hamiltonian in equation (5) is a Hermitian operator, and the eigenvalues of a Hermitian operator must be real, so 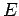 is real. This means that the solutions
is real. This means that the solutions 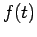 are purely oscillatory, since
are purely oscillatory, since 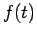 never changes in magnitude
never changes in magnitude
(recall Euler's formula 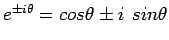 ).
).
Thus if
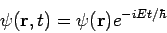 | (7) |
Then the total wave function 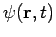 differs from
differs from 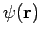 only by a phase factor of constant magnitude.
only by a phase factor of constant magnitude.
There are some interesting consequences of this. First of all, the quantity 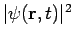 is time independent, as we can easily show:
is time independent, as we can easily show:
 | (8) |
Secondly, the expectation value for any time-independent operator is also time-independent, if 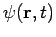 satisfies equation (7). By the same reasoning applied above,
satisfies equation (7). By the same reasoning applied above,
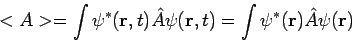 | (9) |
For these reasons, wave functions of the form (7) are called stationary states. The state  is stationary,'' but the particle it describes is not!
is stationary,'' but the particle it describes is not!
Equation (7) represents a particular solution to equation (1).
The general solution to equation (1) will be a linear combination of these particular solutions, that is
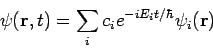
Consider one dimensional closed box of width L. A particle of mass ‘m’ is moving in a one-dimensional region along X-axis specified by the limits x=0 and x=L as shown in fig. The potential energy of particle inside the box is zero and infinity elsewhere.
Potential energy V(x) is of the form
V(x) = {o; if o<x<L
∞: elsewhere
The one-dimensional time independent Schrodinger wave equation is given by
d2ψ/dx2+ 2m/Ћ2[E-V] ψ=0 (1)
Here the partial derivatives have been changed because equation now contains only one variable that is x-Co-ordinate. Inside the box V(x) =0
Therefore, the Schrodinger equation in this region becomes
d2/ψ/dx2+ 2m/Ћ2Eψ=0
Or d2ψ/dx2+ K2ψ=0 (2)
Where k= 2mE/Ћ2 (3)
k is called the Propagation constant of the wave associated with particle and it has dimensions reciprocal of length.
The general solution of eq (2) is
Ψ=A sin Kx + B cos K x (4)
Where A and B are arbitrary conditions and these will be determined by the boundary conditions.
(ii) Boundary Conditions
The particle will always remain inside the box because of infinite potential barrier at the walls. So, the probability of finding the particle outside the box is zero that is .ψx=0 outside the box.
We know that the wave function must be continuous at the boundaries of potential well at x=0 and x=L, i.e.
Ψ(x)=0 at x=0 (5)
Ψ(x)=0 at x= L (6)
These equations are known as Boundary conditions.
(iii) Determination of Energy of Particle
Apply Boundary condition of eq.(5) to eq.(4)
0=A sin (X*0) +B cos (K*0)
0= 0+B*1
B=0 (7)
Therefore eq.(4) becomes
Ψ(x) = A sin Kx (8)
Applying the boundary condition of eq.(6) to eq.(8) ,we have
0=A sin KL
Sin KL=0
KL=nπ
K=nπ/L (9)
Where n= 1, 2, 3 – – –
A Cannot be zero in eq. (9) because then both A and B would be zero. This will give a zero wave function every where which means particle is not inside the box.
Wave functions. Substitute the value of K from eq. (9) in eq. (8) to get
Ψ(x)=A sin(nπ/Lx)
As the wave function depends on quantum number π so we write it ψn. Thus
Ψn=A sin (nπx/L)0<x<L
This is the wave function or eigen function of the particle in a box.
Ψn=0 outside the box
Energy value or Eigen value of particle in a box: Put this value of K from equation (9) in eq. (3)
nπ/L = 2m E/Ћ2
Squaring both sides
n2π2/L2=2mE/Ћ2
E=n2π2Ћ2/2mL2
Where n= 1, 2, 3… Is called the Quantum number
As E depends on n, we shall denote the energy of particle arEn. Thus
En= n2π2Ћ2/2mL2 (10)
This is the eigen value or energy value of the particle in a box.
It was Max Born, in 1926, who linked the function of the quantum wave to empirical meaning. He found that squaring the wave function module gives the density of the probability of occurrence, like observing an electron. A diffracted electron can be found in any space for which the wave function is not zero. If the meaning of the wave function is limited to what the square of the module refers to, what happens between the diffraction and the subsequent detection of the electron (the intermediate period) is irrelevant. This is vital for any realistic microscopic domain theory.
So what happens with the interim period? Born's discovery is consistent with the electron found somewhere, anywhere or nowhere in the intermediate period. Maybe you can imagine even more possibilities! The important thing is to find out the importance or even the relevance of the difference between the three possibilities. What we do know is that the question has no relevance for the probability that the electron is somewhere, if observed. That is why what is happening in the intermediate period can form the basis for any number of different quantum interpretations, provided that the wave function and its importance are never lost sight of. In this way, each interpretation has the same mathematical result: they are all equally successful, at least it is often said that they are.
The question of the intermediate period becomes somewhat more complicated when you realize that the wave function is relevant for an abstract configuration space, not for a fourth dimensional physical space or space-time. This leaves open the possibility that what is happening in the configuration space and in the physical space is different, because during the intermediate period their mutual relevance is indeterminate. What happens in the configuration space is mathematical and not physical. This question of relevance is the foundation of the perceived incompleteness that influences quantum mechanics.
The probability amplitude for a free particle with momentum 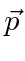 and
and
Energy 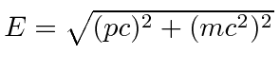
Is the complex wave function
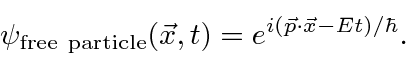
Note that 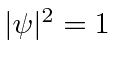 everywhere so this does not represent a localized particle. In fact we recognize the wave property that, to have exactly one frequency, a wave must be spread out over space.
everywhere so this does not represent a localized particle. In fact we recognize the wave property that, to have exactly one frequency, a wave must be spread out over space.
We can build up localized wave packets that represent single particles by adding up these free particle wave functions (with some coefficients).
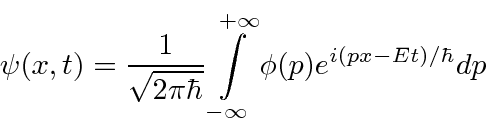
(We have moved to one dimension for simplicity.) Similarly we can compute the coefficient for each momentum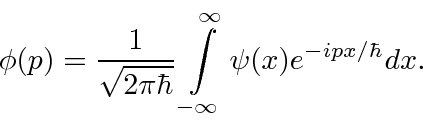
These coefficients, 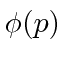 , are actually the state function of the particle in momentum space. We can describe the state of a particle either in position space with
, are actually the state function of the particle in momentum space. We can describe the state of a particle either in position space with 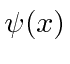 or in momentum space with
or in momentum space with 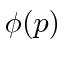 . We can use
. We can use 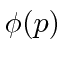 to compute the probability distribution function for momentum.
to compute the probability distribution function for momentum.
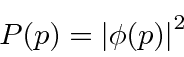
We will show that wave packets like these behave correctly in the classical limit, vindicating the choice we made for
1.8  and
and 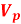 relation Uncertainty principle
relation Uncertainty principle
Phase and group velocity are two important and related concepts in wave mechanics. They arise in quantum mechanics in the time development of the state function for the continuous case that is wave packets.
Harmonic Waves and Phase Velocity
A one-dimensional harmonic wave as shown in figure 1 is described by the equation,
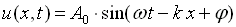
Where A0 is the wave amplitude,
w is the circular frequency;
k is the wave number;
And 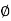 is an initial, constant phase.
is an initial, constant phase.
Sometimes the wave number is referred to as the spatial frequency or propagation constant.

Figure 1: Harmonic Wave
This is a monochromatic wave of one frequency. There are no strictly monochromatic waves in nature.
For example, the generating source of the wave may move slightly, introducing spurious frequencies.
In general, these waves propagate without warping. That is, the phase 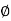 (x, t) is a constant:
(x, t) is a constant:
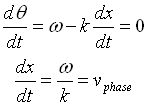
vphase is the phase velocity for a wave.
- For sending information, these waves are not useful because they are the same throughout time and space. Some must be modulated, such as frequency or amplitude, in order to convey information.
- The resulting wave may be a perturbation that acts over a short distance, that is a wave packet. This wave packet can be considered to be a superposition of a number of harmonic waves, that is in other words a Fourier series or integral.
Group Velocity
In order to convey information, it is essential to have a thing more than a simple harmonic wave is required. However, the superposition of many such waves of varying frequencies can result in an "envelope" wave and a carrier wave within the envelope.
The envelope can transmit data.
A simple example is the superposition of two harmonic waves with frequencies that are very close (w1 ~w2) and of the same amplitude. The equations for the motion are,
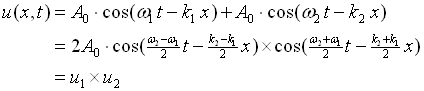
The plot of such a wave is shown in Figure 2.
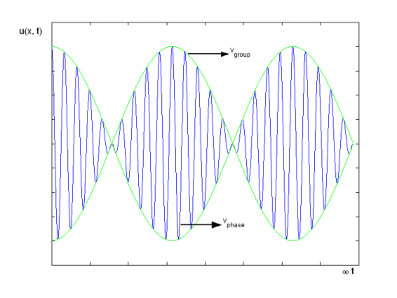
Figure 2: Group Velocity
The envelope (the green line) is given by u1 and travels at the group velocity. The carrier wave (the blue line) travels at the phase velocity and is given by u2. The wave packet moves at the group velocity. It is the envelope which carries information. Group velocity is given by,
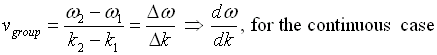
Phase and group velocity are related through Rayleigh's formula,

If the derivative term is zero, group velocity equals phase velocity.
In this case, there is no dispersion.
Dispersion is when the distinct phase velocities of the components of the envelope cause the wave packet to "spread out" over time.
.