Unit 1
DC Circuits
Ideal and practical Voltage and Current source:
A voltage source is a device which provides a constant voltage to load at any instance of time and is independent of the current drawn from it. This type of source is known as an ideal voltage source. Practically, the ideal voltage source cannot be made. It has zero internal resistance. It is denoted by this symbol.
Fig: Voltage source symbol
Ideal Voltage Source
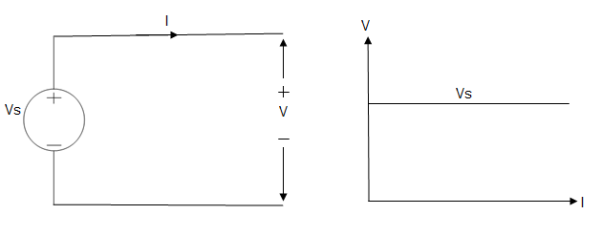
Fig: Ideal Voltage Source
The graph represents the change in voltage of the voltage source with respect to time. It is constant at any instance of time.
Voltage sources that have some amount of internal resistance are known as a practical voltage source. Due to this internal resistance, voltage drop takes place. If the internal resistance is high, less voltage will be provided to load and if the internal resistance is less, the voltage source will be closer to an ideal voltage source. A practical voltage source is thus denoted by a resistance in series which represents the internal resistance of source.
Practical Voltage source
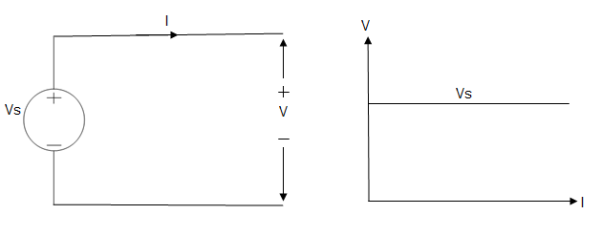
Fig: Practical Voltage source
The graph represents the voltage of the voltage source with respect to time. It is not constant but it keeps on decreasing as the time passes.
Current source
A current source is a device which provides the constant current to load at any time and is independent of the voltage supplied to the circuit. This type of current is known as an ideal current source; practically ideal current source is also not available. It has infinite resistance. It is denoted by this symbol.
Ideal Current source
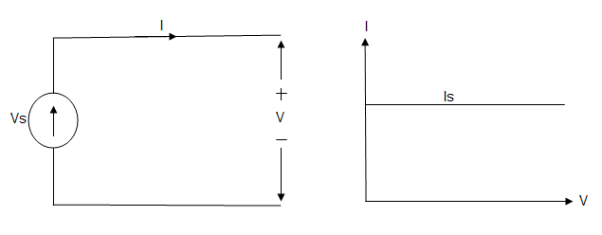
Fig: Ideal Current source
The graph represents the change in current of the current source with respect to time. It is constant at any instance of time.
Why ideal Current source has infinite resistance?
A current source is used to power a load, so that load will turn on. We try to supply 100% of the power to load. For that, we connect some resistance to transfer 100% of power to load because the current always takes the path of least resistance. So, in order for current to go to the path of least resistance, we must connect resistance higher than load. This is why we have the ideal current source to have infinite internal resistance. This infinite resistance will not affect voltage sources in the circuit.
Practical Current source
Practically current sources do not have infinite resistance across there but they have a finite internal resistance. So the current delivered by the practical current source is not constant and it is also dependent somewhat on the voltage across it.
A practical current source is represented as an ideal current source connected with resistance in parallel.
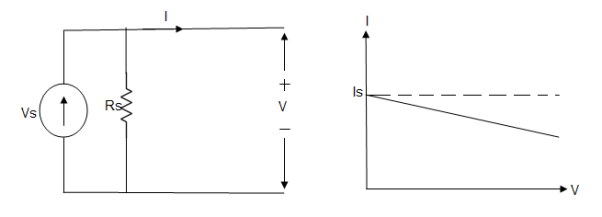
Fig; Practical Current source
The graph represents the current of the current source with respect to time. It is not constant but it also keeps on decreasing as the time passes.
Examples of current and voltage sources
The examples of current source are solar cells, transistors and examples of some voltage sources are batteries and alternators.
This was all about ideal and practical sources of power. The ideal sources are very useful for calculations in theory but as ideal sources are not practically possible, only practical sources are used in practical circuits. The batteries we use are a practical source of power and the voltage and current decreases as we use it. Thus both are useful to us in their own ways.
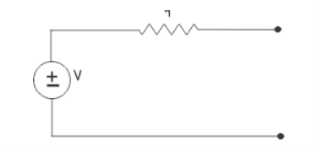
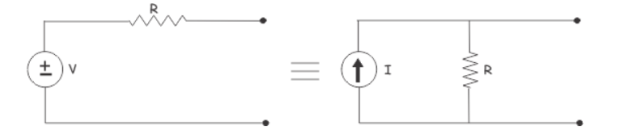
Electrical source transformation is a method of replacing voltage source in a circuit by its equivalent current source and current source by its equivalent voltage source.
Let us take a simple voltage source along with a resistance connected in series with it. This series resistance normally represents the internal resistance of a practical voltage source.
Short circuit the output terminals of the voltage source circuit as shown below,
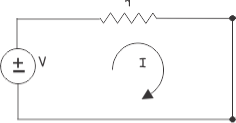
Now applying Kirchhoff Voltage law in the circuit, we get
V = Ir ---------------------(i)
Where, I is the current which delivers by the voltage source when it is short circuited.
Now, let us take a current source of same current I which produces same open circuit voltage at its open terminals as shown below,
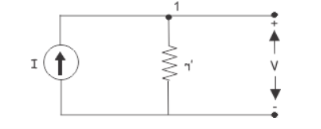
Now, applying Kirchhoff’s current law at node 1, of the above circuit, we get,
I = V / r’ ----- V = I r’ --------(ii)
From equation (i) and (ii) we get
r = r’
The open circuit voltage of both the sources is V and short circuit current of both sources is I. The same resistance is connected in series in voltage source is connected in parallel in its equivalent current source.
So, these voltage source and current source are equivalent to each other.
A current source is dual form of a voltage source and a voltage source is dual form of a current source. A voltage source can be converted into an equivalent current source and a current source can also be converted into an equivalent voltage source.
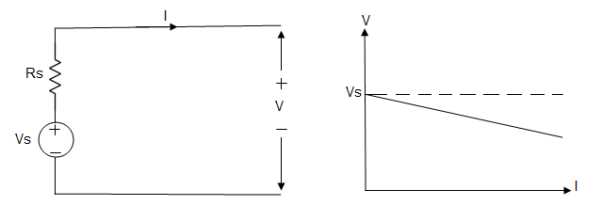
Voltage Source to Current Source Conversion
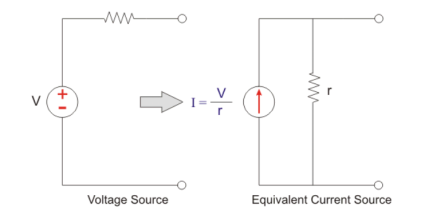
Assume a voltage source with terminal voltage V and the internal resistance r. This resistance is in series. The current supplied by the source is equal to:
I = V / r
When the source of the terminals are shorted.
This current is supplied by the equivalent current source and the same resistance r will be connected across the source. The voltage source to current source conversion is shown in the following figure.
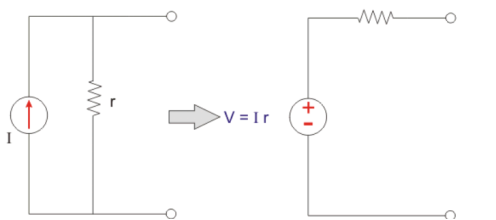
Current source to Equivalent voltage source:
Assume a current spurce with the value I and internal resistance r. Now according to the Ohms law the voltage across the source can be calculated as
V = Ir
Hence, voltage appearing, across the source, when terminals are open, is V.
Current source Equivalent voltage source
Ohm’s principal discovery was that the amount of electric current through a metal conductor in a circuit is directly proportional to the voltage impressed across it, for any given temperature. Ohm expressed his discovery in the form of a simple equation, describing how voltage, current, and resistance interrelate:
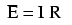
In this algebraic expression, voltage (E) is equal to current (I) multiplied by resistance (R). Using algebra techniques, we can manipulate this equation into two variations, solving for I and for R, respectively:

The algebraic sum of currents meeting at a junction or node in a electric circuit is zero ② or the summation of all incoming current is always equal to summation of all outgoing current in an electrical network.
Explanation
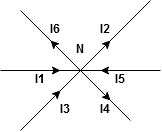
Assuming the incoming current to be positive and outgoing current negative we have
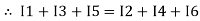
Ie incoming current = ∑ outgoing current thus, the above Law can also be stated as the sum of current flowing towards any junction in an electric circuit is equal to the sum of currents flowing away from that junction
incoming current = ∑ outgoing current thus, the above Law can also be stated as the sum of current flowing towards any junction in an electric circuit is equal to the sum of currents flowing away from that junction
Kirchhoff’s Voltage Law (KVL)
Statement : the algebraic summation of all Voltage in any closed circuit or mesh of loop zero.
Ie ∑ Voltage in closed loop = 0 the summation of the Voltage rise (voltage sources) is equal to summation of the voltage drops around a closed loop in 0 circuit for explanation from here
Determination of sigh and direction of currents (Don’t write in exams just for understanding)
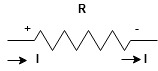
Current entering a resistor is +ve and leaving should be –ve
Now

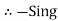
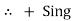
Potential Rise Potential Drop
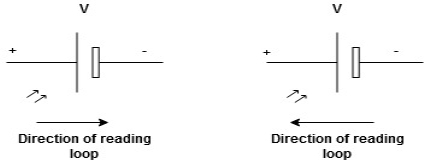
We are reading from +V to –V we are reading from –V to +V
 potential drops
potential drops  potential rise
potential rise
 -V
-V  +V
+V
Given Circuit

First identify no of loops and assign direction of current flowing in loop
Note : no of loops in circuit = No, of unknown currents = no, of equations in the circuit
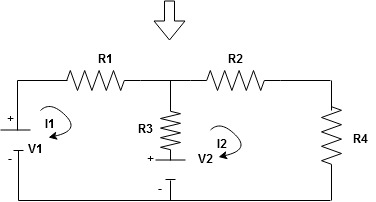
Note : keep loop direction and current direction same ie either clockwise or anticlockwise for all loops I1 I2
Now according to direction of direction assign signs (+ve to –ve) to the resistors
Note : voltage sources (V) polarities does not change is constant.
Note: for common resistor between 2 loops appearing in the circuit like R3 give signs according to separate loops as shown

When considering only loop no 1 (+ R3 - )
- B
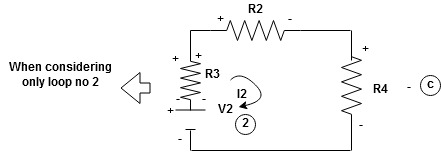
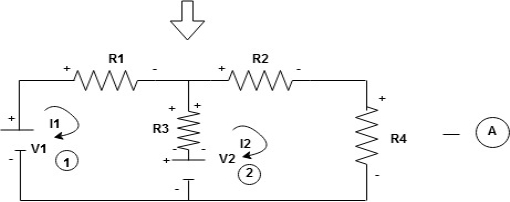
Now consider diagram A and write equations
Two loops  two unknown currents
two unknown currents  two equation
two equation
Apply KVL for loop ① [B. Diagram ]
(+ to drop -) = - sign and (- to rise +) = + sign
 for drop = -sign
for drop = -sign
 for rise = + sign
for rise = + sign
-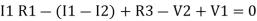
-(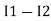 ) R2 is considered because in R3,2 currents are flowing
) R2 is considered because in R3,2 currents are flowing 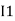 and
and 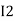 and we have taken (
and we have taken (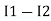 ) because we are considering loop no 1 and current flowing is
) because we are considering loop no 1 and current flowing is 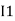 in loop no 1
in loop no 1
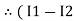 )
)
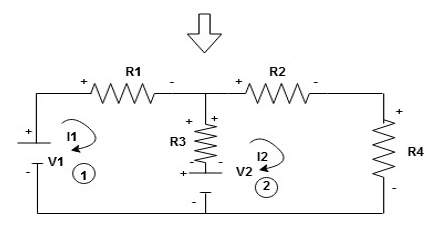
Similarly for loop no. 2 currents flowing is 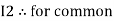 resistor R3 it should be
resistor R3 it should be  )R3
)R3
Consider loop no. 1 apply KVL
-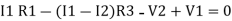 …….①
…….①
-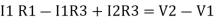
Consider loop no. 2 apply KVL
- …….②
…….②
-
After solving equation ① and ② we will get branch current 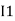 and
and 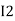
This is only applicable to circuits with linear elements.
If two or more than two independent sources (voltage or current) are operating in the circuit than voltage across any element or current through any element is sum of current and voltages due to individual sources.
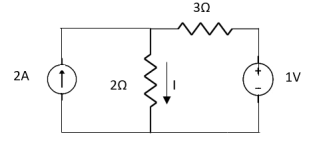
Question 1. Find the current through 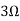 resistance.
resistance.
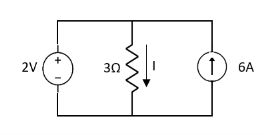
Solution:
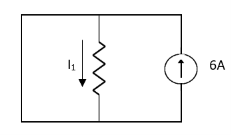
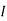 1= 0
1= 0
 2=
2=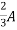
 1 +
1 + 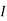 2
2 
Special Case:
Since two voltage sources with different magnitude in parallel which cannot be connected as in single branch two different current is not possible (if 5V than I = zero).
Question:
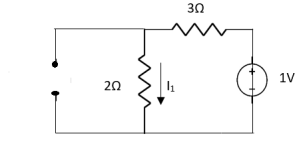
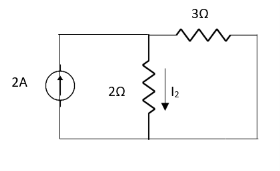
 1 =
1 = 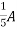
 2 =
2 = 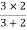
=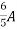
 1 +
1 + 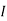 2
2
= 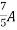
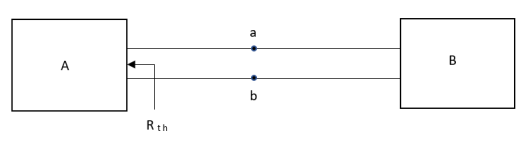
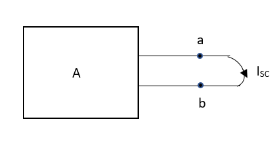
Thevenin’s equivalent of A
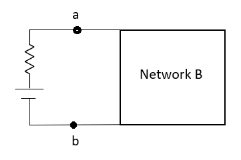
Norton’s equivalent of A
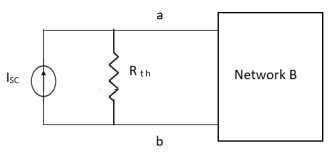
 sc = Vth/Rth
sc = Vth/Rth
- Norton’s equivalent is obtained by source conversion of thevenin’s equivalent circuit.
CONDITIONS FOR APPLICATION
- For network A:
- Network A should contain linear elements.
- Network A can have independent and dependent current and voltage source.
- If network A has dependent source than controlling parameter must lie in network A itself.
- Network A should not have any source coupling and magnetic coupling.
- For network B:
- It can have linear and non linear elements.
- It can have dependent and independent voltage and current sources.
- It should not have any source and magnetic coupling with network A.
Method for finding Rth :
Firstly, open circuit terminal A and B.
- If network is operating with only independent sources:
- Make all sources zero in network A.
- Find out the equivalent resistance across terminal A and B.
2. If network A is operating with independent and dependent sources:
- Make all independent sources zero in network A.
- Connect a generation between A and B.
3. If network is operating with only dependent sources:
Connect generation between A and B
Method for Vth:
First open circuit terminal A and B.
Find out the voltage between A and B this is Vth

Method for Isc:
- Isc =
- Remove network B and S.C. The terminal A and B and current from terminal A to B Isc.
Question:
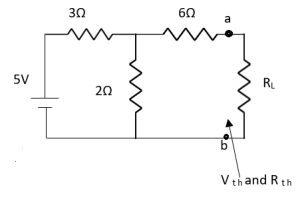
Answer:
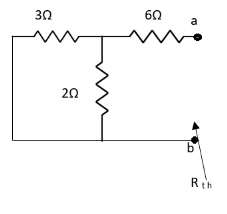
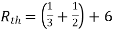
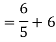
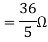
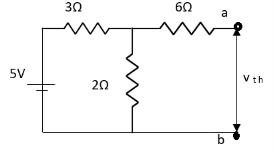
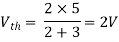
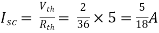
Finding Isc from circuit directly:
By KCL,
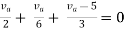
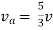
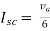
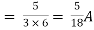
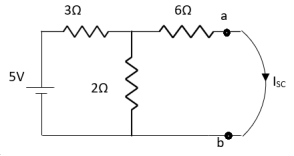
Question:
Answer

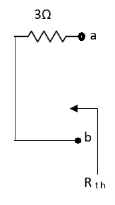
Also, clear from circuit that Vth = 1V.
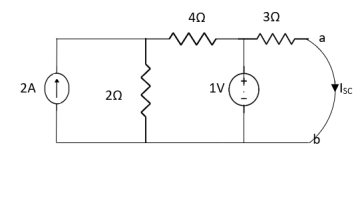
By applying KVL we get,
1-3Isc=0
Isc= A
A
Que:

Ans;
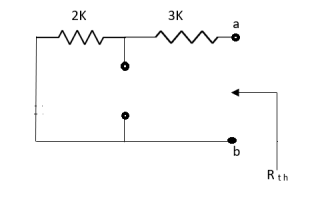
Rth=3k+2k=5k
By applying KVL we get

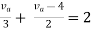
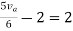
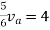
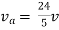
Therefore, 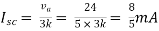
Question:
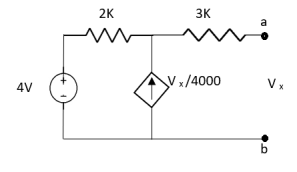
Solution: For Rth
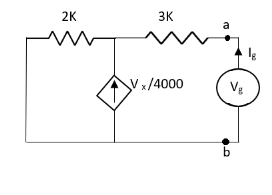
By KCL,
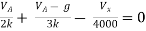
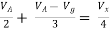

But, 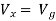

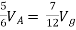
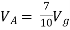
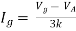
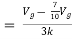
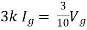
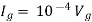
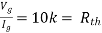
By KVL,
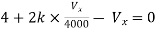
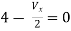
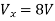
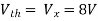
Question:
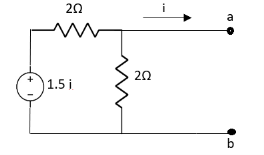
Solution: Since, no independent source is present so,
Isc = 0
And we know that,
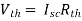
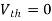
Since Rth cannot be zero
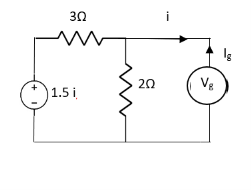

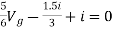
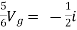
But 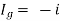
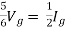
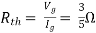
In loop analysis we use mesh which is a loop that does not have any other loops inside it. A mesh starts at a node and traces a path around a circuit, returning to the original node without hitting any nodes more than once.
To obtain the mesh equations to be able to interpret the circuit. The mesh equations are obtained by
1. Applying Kirchhoff's voltage law (KVL) to each mesh in the circuit.
2. Express the voltages of elements in terms of the mesh currents.
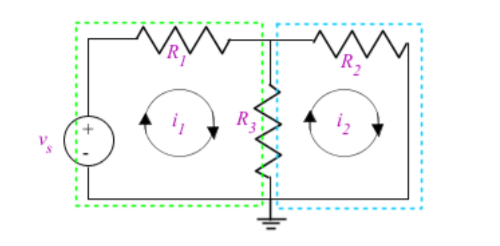
The circuit has 2 meshes in it outlined in green and blue dotted lines. The currents i1 and i2 are the currents around a mesh.
The method behind mesh analysis is to examine the mesh in terms of the voltages of each element and express that with mesh currents. Using Ohm's law, we can express the voltage across R1 as R1.i1
Use this approach across a circuit applying KVL to find the mesh equations, then use these equations to solve for unknown current.
In case where a dependent source is present in a circuit, the controlled current or voltage of that source must also be expressed by the mesh currents. Examine the circuit and find which part of the circuit controls the dependent source and express that voltage or current with the mesh currents that affect it.

In this circuit, a dependent source generates voltage depending on the current at va. To express this in terms of the mesh currents examine the circuit which shows that the current is equal to the mesh current. Therefore, the dependent source will force volts into the system, and now mesh analysis can be performed to solve for the remaining unknowns.
Nodal Analysis:
We use nodal analysis on circuits to obtain KCL equations used to solve for voltage and current in a circuit. The number of KCL equations is one less than the number of nodes that a circuit has. The extra node may be referred as reference node. If a circuit contains ground which ever node the ground is connected to is selected as the reference node. This is used to find the voltage differences at each other node in the circuit with respect to the reference.
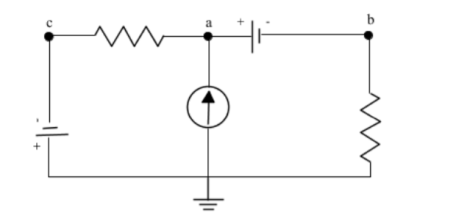
Ideally, we set the voltage to 0 V at the reference node to simplify calculations, however it can be set to any value if the other nodes account for the different reference voltage. Solving the node equations can provide us with the node voltages.
The node equations are obtained by completing two things:
1. Express the current through an element in terms of the node voltages.
2. Apart from the reference node, apply KCL to each other node in the circuit.
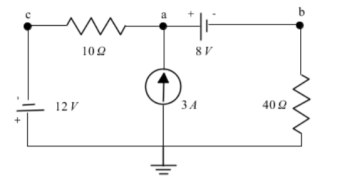
Here, node c is an example of a super node which is a connection between two nodes via an independent or dependant voltage source. Because super nodes are connected to a voltage source we can find their voltage immediately.
In this case the voltage across the source will be 12 =0-vc = -12V . Similarly node
A is related to node b as super node va = vb + 8V. We can substitute va and vc into our KCL equations to solve for vb.
Calculate KCL equations at node a in figure 3. The current source is directing current into node a . Assume the current flows away from a towards node b and c.
The KCL equation for node a is
[A] = ib + ic
The current across the resistor represented by the node voltages is found through Ohm's law as the potential across the element divided by the resistance. Note the assumed direction of the current to ensure the correct polarity of the difference in potential.
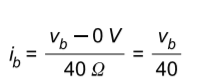
The current through node c will be equivalent to the potential across the resistor10 Ω divided by the resistance.
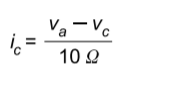
Substituting in the currents and and using the equations for and , the KCL equation at node A is found to be
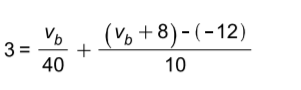
Solving we get va =16V and vb =8V .
Star to delta conversion to final equivalent resistance
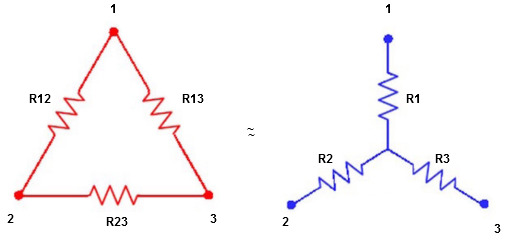
We know that (from delta to star conversion)
R1 = 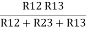 …….①
…….①
R2 = 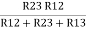 …..②
…..②
R1 = 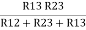 ……③
……③
Multiply ① X ② L.H.S and R.H.S
R1 R2 = …….④ where
…….④ where 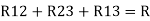
Similarly multiply ② X ③
R2 R3 = …….⑤
…….⑤
And ③ X①
R1 R3 =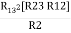 …….⑥
…….⑥
Now add equation ④, ⑤, and ⑥ L.H.S and R.H.S

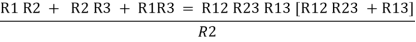

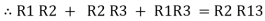 ……refer eq. ②
……refer eq. ②
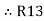 =
=  +
+ 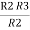 +
+ 
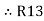 =
= 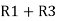 +
+ 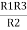
(Delta)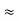 star star
star star
Similarly R23 = R2+R3 + 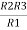
R23 = R1+R2 + 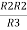
- Delta to Star Conversion to Find (Req.)
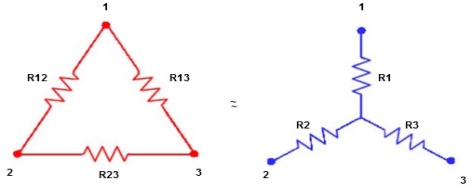
- Equivalent resistance between ① and ②
Delta 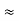 Star
Star
= R12// (R23 + R13) =R1 + R2
= 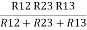
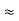 = R1 + R2
= R1 + R2
= 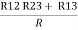
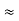
Here let R = R12 + R23 + R13
- Similarly we can find Req. Between 2 and 3
= 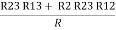
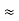 R2 + R3
R2 + R3
- Similarly we can find req. Between 1 and 3
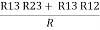
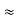 R1 + R3
R1 + R3
Now the 3 equations after equating L.H.S. And R.H.S
R1 + R2 = 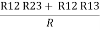 …….①
…….①
R2 + R3 = 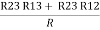 ……②
……②
R1 + R3 = 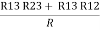 …..③
…..③
Now subtract ② and ① on L.H.S. And R.H.S
R2+ R3 – R1 – R2 = 
 R3 – R1 =
R3 – R1 = 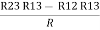 …..④
…..④
Now add equation ④ and ③
R3 – R1 + R1 + R3 = 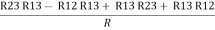
2R3 = 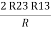

Similarly R1 = 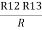
And R2 = R23 R12/R where R = R12 + R23 + R13
Ie star equivalent from delta network is ratio of product of adjacent branches in delta to the addition of all branches in delta.