Unit-4
Multivariable Differential Calculus
First order partial differentiation-
Let f(x, y) be a function of two variables. Then the partial derivative of this function with respect to x can be written as 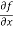 and defined as follows:
and defined as follows:
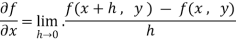
Now the partial derivative of f with respect to f can be written as 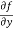 and defined as follows:
and defined as follows:
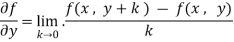
Note: a. While calculating partial derivatives treat all independent variables, other than the variable with respect to which we are differentiating , as constant.
b. We apply all differentiation rules.
Higher order partial differentiation-
Let f(x , y) be a function of two variables. Then its second-order partial derivatives, third order partial derivatives and so on are referred as higher order partial derivatives.
These are second order four partial derivatives:
(a) 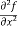 =
= 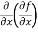
(b) 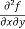 =
= 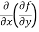
(c)  =
= 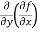
(d) 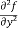 =
= 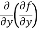
b and c are known as mixed partial derivatives.
Similarly we can find the other higher order derivatives.
Example-1: -Calculate 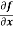 and
and 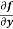 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Sol. To calculate 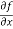 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
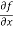 =
= 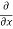 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 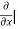 3x³] -
3x³] - 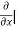 5y²] +
5y²] + 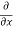 [2xy] -
[2xy] -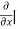 8x] +
8x] +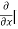 4y] -
4y] - 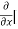 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
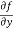 =
= 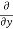 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 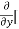 3x³] -
3x³] - 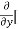 5y²] +
5y²] + 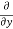 [2xy] -
[2xy] -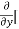 8x] +
8x] +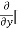 4y] -
4y] - 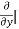 20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Example-2: Calculate 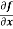 and
and 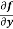 for the following function
for the following function
f( x, y) = sin(y²x + 5x – 8)
Sol. To calculate 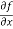 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
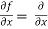 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)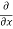 (y²x + 5x – 8)
(y²x + 5x – 8)
= (y² + 50)cos(y²x + 5x – 8)
Similarly partial derivative of f(x,y) with respect to y is,
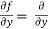 [sin(y²x + 5x – 8)]
[sin(y²x + 5x – 8)]
= cos(y²x + 5x – 8)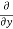 (y²x + 5x – 8)
(y²x + 5x – 8)
= 2xycos(y²x + 5x – 8)
Example-3: Obtain all the second order partial derivative of the function:
f( x, y) = ( x³y² - xy⁵)
Sol.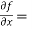 3x²y² - y⁵,
3x²y² - y⁵, 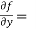 2x³y – 5xy⁴,
2x³y – 5xy⁴,
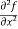 =
= 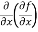 = 6xy²
= 6xy²
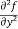 =
= 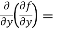 2x³ - 20xy³
2x³ - 20xy³
 =
= 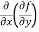 = 6x²y – 5y⁴
= 6x²y – 5y⁴
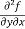 =
=  = 6x²y - 5y⁴
= 6x²y - 5y⁴
Example-4: Find
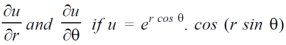
Sol. First we will differentiate partially with repsect to r,
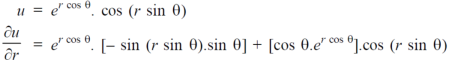
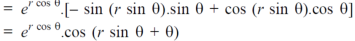
Now differentiate partially with respect to θ, we get
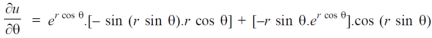
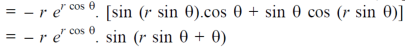
Example-5: if,
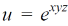
Then find.
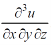
Sol-
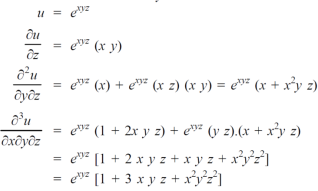
Example-6: if 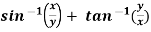 , then show that-
, then show that- 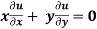
Sol. Here we have,
u = 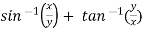 …………………..(1)
…………………..(1)
Now partially differentiate eq.(1) w.r to x and y , we get
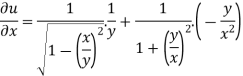
= 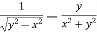
Or
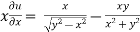 ………………..(2)
………………..(2)
And now,
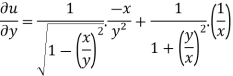
= 
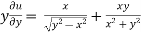 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
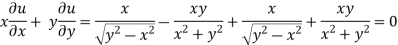
Hence proved.
Key takeaways-
1. 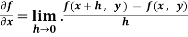
(a) 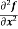 =
= 
(b) 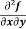 =
= 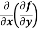
(c)  =
= 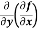
(d) 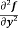 =
= 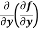
When we measure the rate of change of the dependent variable owing to any change in a variable on which it depends, when none of the variable is assumed to be constant.
Let the function, u = f( x, y), such that x = g(t) , y = h(t)
ᵡ Then we can write,
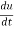 =
= 
= 
This is the total derivative of u with respect to t.
Change of variable-
If w = f (x, y) has continuous partial variables fxand fyand if x = x (t), y = y (t) are
Differentiable functions of t, then the composite function w = f (x (t), y (t)) is a
Differentiable function of t.
In this case, we get,
 fx(x (t), y (t)) x’(t)+ fy(x(t), y (t)) y’(t).
fx(x (t), y (t)) x’(t)+ fy(x(t), y (t)) y’(t).
Example-:1 let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find 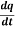 .
.
Sol. : . =
. = 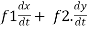
Where, f1 = 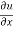 , f2 =
, f2 = 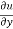
In this example f1 = 4 , f2 = 3
Also,  3t² + 2t ,
3t² + 2t , 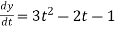
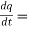 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(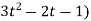
= 21t² + 2t – 3
Example-2: Find 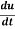 if u = x³y⁴ where x = t³ and y = t².
if u = x³y⁴ where x = t³ and y = t².
Sol. As we know that by definition, 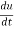 =
= 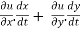
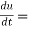 3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
3x²y⁴3t² + 4x³y³2t = 17t¹⁶.
Example-3: if w = x² + y – z + sintand x + y = t, find
(a) 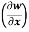 y,z
y,z
(b) 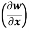 t, z
t, z
Sol. With x, y, z independent, we have
t = x + y, w = x²+ y - z + sin (x + y).
Therefore,
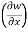 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)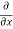 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
Thus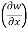 t, z = 2x - 1
t, z = 2x - 1
Example-4: If u = u( y – z , z - x , x – y) then prove that  = 0
= 0
Sol. Let,
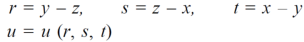
Then,
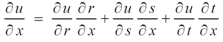
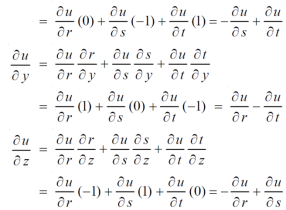
By adding all these equations we get,
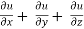 = 0 hence proved.
= 0 hence proved.
Example-5: if φ( cx – az , cy – bz) = 0 then show that ap + bq = c
Where p = 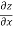 q =
q = 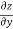
Sol. We have,
φ( cx – az , cy – bz) = 0
φ( r , s) = 0
Where,
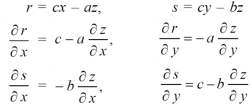
We know that,
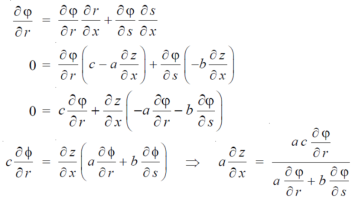
Again we do,
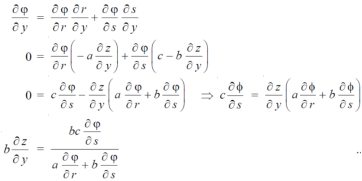
By adding the two results, we get
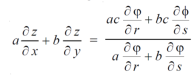

Example-6: If z is the function of x and y , and x = 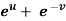 , y =
, y = 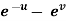 , then prove that,
, then prove that,
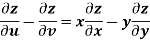
Sol. Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
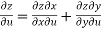 ……………….(1)
……………….(1)
And,
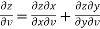 ………………..(2)
………………..(2)
Also there is,
x = 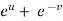 and y =
and y = 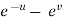 ,
,
Now,
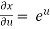 ,
, 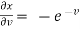 ,
, 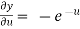 ,
, 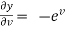
From equation(1) , we get
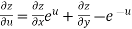 ……………….(3)
……………….(3)
And from eq. (2) , we get
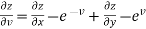 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
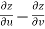 =
= 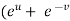 )
)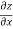 – (
– (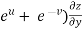
= x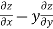
Hence proved.
Key takeaways:
- Let the function, u = f( x, y), such that x = g(t) , y = h(t)
ᵡ Then we can write,
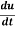 =
= 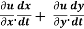
= 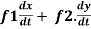
This is the total derivative of u with respect to t.
A composite function is a composition / combination of the functions. In this value of one function depends on the value of another function. A composite function is created when one function is put in another.
Let 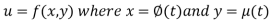
i.e 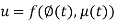
To differentiate composite function chain rule is used:
Chain rule:
- If
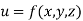 where x,y,z are all the function of t then
where x,y,z are all the function of t then
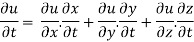
2. If 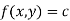 be an implicit relation between x and y .
be an implicit relation between x and y .
Differentiating with respect to x we get
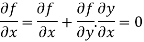
We get 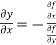
Example1 : If 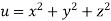 where
where 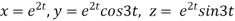 then find the value of
then find the value of 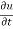 ?
?
Given 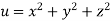
Where 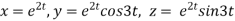
By chain rule
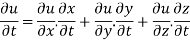
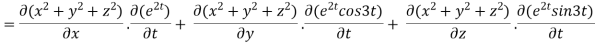


Now substituting the value of x ,y,z we get
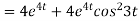 -6
-6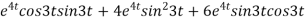

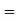 8
8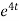
Example2 :If 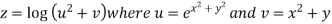 then calculate
then calculate 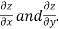
Given 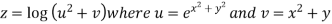
By Chain Rule
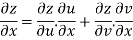
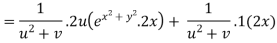
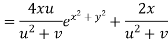
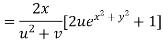
Putting the value of u = 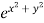
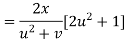
Again partially differentiating z with respect to y
By Chain Rule
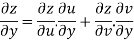
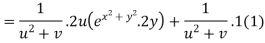
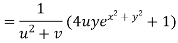
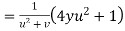 by substituting value
by substituting value 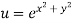
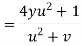
Example 3 :If 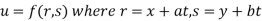 .
.
Show that 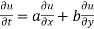
Given 
Partially differentiating u with respect to x and using chain rule
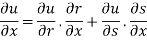

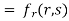 ………(i)
………(i)
Partially differentiating z with respect to y and using chain rule
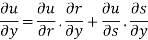

= 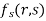 ………..(ii)
………..(ii)
Partially differentiating z with respect to t and using chain rule
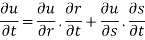
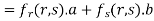
Using (i) and (ii) we get

Hence 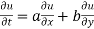
Example4 : If 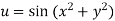 where the relation is
where the relation is 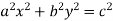 .
.
Find the value of 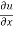
Let the given relation is denoted by 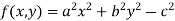
We know that 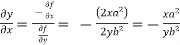
Differentiating u with respect to x and using chain rule
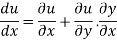
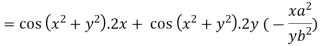

Example5 : If 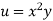 and the relation is
and the relation is 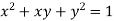 . Find
. Find 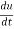
Given relation can be rewrite as
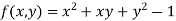 .
.
We know that
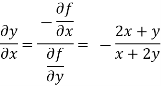
Differentiating u with respect to x and using chain rule
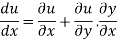

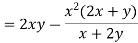
Implicit differentiation-
Let f(x,y) = 0
Where y = ∅(x)
By the chain rule , with x = x and y = ∅(x), we get
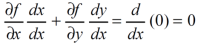
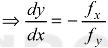
Here we assume that y is a differentiable funtion of x.
Example-1: if ∅ is a differentiable function such that y = ∅(x) satisfies the equation
x³ + y³ +sin xy = 0 then find 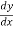 .
.
Sol. Suppose f(x,y) = x³ + y³ +sin xy
Then ,
fᵡ = 3x² + y cos xy
Fy = 2y + x cos xy
So ,
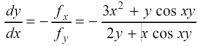
Example-2:
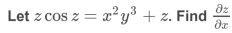
Sol. Take partial derivative on both side w.r. t. x , treat y as constant
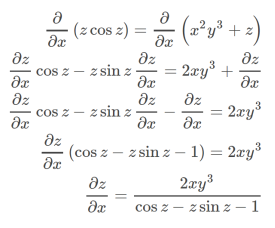
Example-3: if x²y³ + cos y cos z = x² cos x sin y, then find 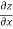
Sol. Differentiate partially w.r.t. x and treat y as constant,
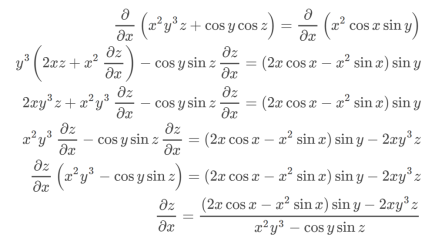
Homogeneous function - A function f(x,y) is said to be homogeneous of degree n if,
f(kx, ky) = kⁿf(x, y)
Here, the power of k is called the degree of homogeneity.
Or
A function f(x,y) is said to be a homogenous function in which the power of each term is the same.
Example:
1. The function-
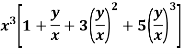
Is a homogeneous function of order 3
Euler’s theorem
Statement – if u = f(x, y) be a homogeneous function in x and y of degree n , then
x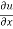 + y
+ y 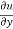 = nu
= nu
Proof:Here u is a homogeneous function of degree n,
u = xⁿ f(y/x) ----------------(1)
Partially differentiate equation (1) with respect to x,
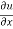 = n
= n f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(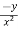 )
)
Now multiplying by x on both sides, we get
x = n
= n f(y/x) + xⁿ f’(y/x).(
f(y/x) + xⁿ f’(y/x).(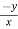 ) ---------- (2)
) ---------- (2)
Again partially differentiate equation (1) with respect to y,
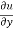 = xⁿ f’(y/x).
= xⁿ f’(y/x).
Now multiplying by y on both sides,
y 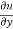 = xⁿ f’(y/x).
= xⁿ f’(y/x). ---------------(3)
---------------(3)
By adding equation (2) and (3),
x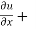 y
y 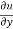 = n
= n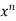 f(y/x) + + xⁿ f’(y/x).(
f(y/x) + + xⁿ f’(y/x).(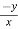 ) + xⁿ f’(y/x).
) + xⁿ f’(y/x).
x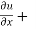 y
y 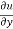 = n
= n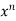 f(y/x)
f(y/x)
Here u = f( x, y) is homogeneous function, then - u = 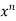 f(y/x)
f(y/x)
Put the value of u in equation (4),
x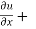 y
y 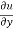 = nu
= nu
Which is the Euler’s theorem.
Corollary: If u is a homogenous function of degree n in x and y then
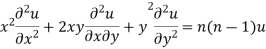
As we know that by Euler’s theorem
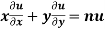 ……(i)
……(i)
Partially differentiating (i) with respect to x we get
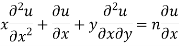
 …..(ii)
…..(ii)
Partially differentiating (i) with respect to y we get
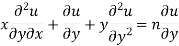
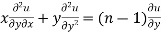 …..(iii)
…..(iii)
Multiplying x by (ii) and y by (iii) then on adding we get
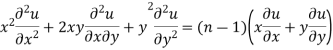
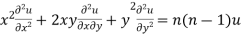 by using (i)
by using (i)
Thus 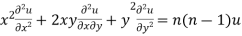
Note: We can directly use the Euler’s theorem and its corollary to solve the problems.
Example: Show that 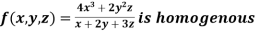
Given 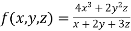
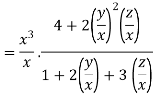
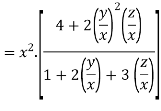
Therefore f(x,y,z) is an homogenous equation of degree 2 in x, y and z
Example: If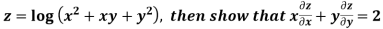
Let 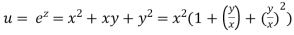
Thus u is an homogenous function of degree 2 in x and y
Therefore by Euler’s theorem
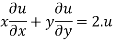
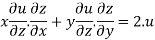
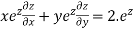 substituting the value of u
substituting the value of u
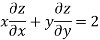
Hence proved
Example: If 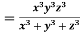 , find the value of
, find the value of 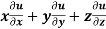
Given 
Thus u is an homogenous function of degree 6 in x ,y and z
Therefore by Euler’s theorem
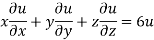
Example: If 
Given 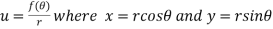
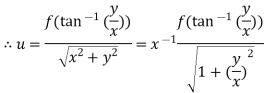
Thus u is an homogenous equation of degree -1 in x and y
Therefore by Euler’s theorem

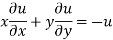
Example1-If u = x²(y-x) + y²(x-y), then show that 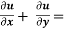 -2 (x – y)².
-2 (x – y)².
Solution - here, u = x²(y-x) + y²(x-y)
u = x²y - x³ + xy² - y³,
Now differentiate u partially with respect to x and y respectively,
 = 2xy – 3x² + y² --------- (1)
= 2xy – 3x² + y² --------- (1)
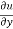 = x² + 2xy – 3y² ---------- (2)
= x² + 2xy – 3y² ---------- (2)
Now adding equation (1) and (2), we get
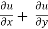 = -2x² - 2y² + 4xy
= -2x² - 2y² + 4xy
= -2 (x² + y² - 2xy)
= -2 (x – y)²
Example: If u = xy + sin(xy), show that 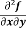 =
= 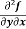 .
.
Solution – u = xy + sin(xy)
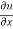 = y+ ycos(xy)
= y+ ycos(xy)
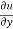 = x+ xcos(xy)
= x+ xcos(xy)
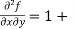 x (- sin(xy).(y)) + cos(xy)
x (- sin(xy).(y)) + cos(xy)
= 1 – xysin(xy) + cos(xy) -------------- (1)
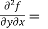 1 + cos(xy) + y(-sin(xy) x)
1 + cos(xy) + y(-sin(xy) x)
= 1 – xysin(xy) + cos(xy) -----------------(2)
From equation (1) and (2),
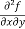 =
= 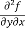
Example-3: If u(x,y,z) = log( tan x + tan y + tan z) , then prove that ,
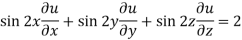
Sol. Here we have,
u(x,y,z) = log( tan x + tan y + tan z) ………………..(1)
Diff. Eq.(1) w.r.t. x , partially , we get
 ……………..(2)
……………..(2)
Diff. Eq.(1) w.r.t. y , partially , we get
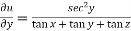 ………………(3)
………………(3)
Diff. Eq.(1) w.r.t. z , partially , we get
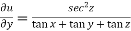 ……………………(4)
……………………(4)
Now multiply eq. 2 , 3 , 4 by sin 2x , sin 2y , sin 2z respectively and adding , in order to get the final result,
We get,
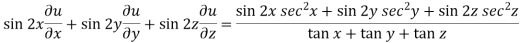
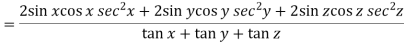
= 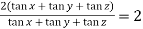
So that,
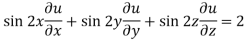
Hence proved.
Key takeaways-
- A function f(x,y) is said to be a homogenous function in which the power of each term is the same.
- If u = f(x, y) be a homogeneous function in x and y of degree n , then
x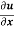 + y
+ y 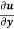 = nu
= nu
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers
4. HK dass, engineering mathematics.