A line code is the code used for data transmission of a digital signal over a transmission line. This process of coding is chosen so as to avoid overlap and distortion of signal such as inter-symbol interference.
Properties of Line Coding
Following are the properties of line coding −
Types of Line Coding
There are 3 types of Line Coding
Unipolar Signaling
Unipolar signaling is also called as On-Off Keying or simply OOK.
The presence of pulse represents a 1 and the absence of pulse represents a 0.
There are two variations in Unipolar signaling −
Unipolar Non-Return to Zero NRZ
In this type of unipolar signaling, a High in data is represented by a positive pulse called as Mark, which has a duration T0 equal to the symbol bit duration. A Low in data input has no pulse.
The following figure clearly depicts this.
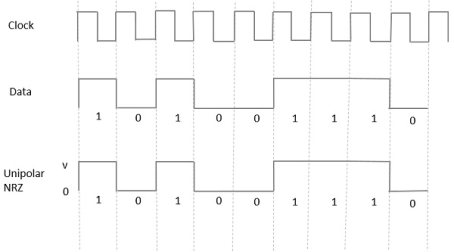
Fig 1 Uni-polar NRZ
Advantages
The advantages of Unipolar NRZ are −
Disadvantages
The disadvantages of Unipolar NRZ are −
Unipolar Return to Zero RZ
In this type of unipolar signaling, a High in data, though represented by a Mark pulse, its duration T0 is less than the symbol bit duration. Half of the bit duration remains high but it immediately returns to zero and shows the absence of pulse during the remaining half of the bit duration.
It is clearly understood with the help of the following figure.
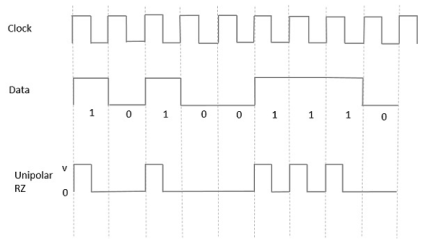
Fig 2 Unipolar RZ
Advantages
The advantages of Unipolar RZ are −
Disadvantages
The disadvantages of Unipolar RZ are −
Polar Signaling
There are two methods of Polar Signaling. They are −
Polar NRZ
In this type of Polar signaling, a High in data is represented by a positive pulse, while a Low in data is represented by a negative pulse. The following figure depicts this well.
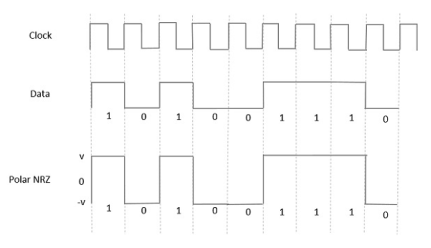
Fig 3 Polar NRZ
Advantages
The advantages of Polar NRZ are −
Disadvantages
The disadvantages of Polar NRZ are −
Polar RZ
In this type of Polar signaling, a High in data, though represented by a Mark pulse, its duration T0 is less than the symbol bit duration. Half of the bit duration remains high but it immediately returns to zero and shows the absence of pulse during the remaining half of the bit duration.
However, for a Low input, a negative pulse represents the data, and the zero level remains same for the other half of the bit duration. The following figure depicts this clearly.
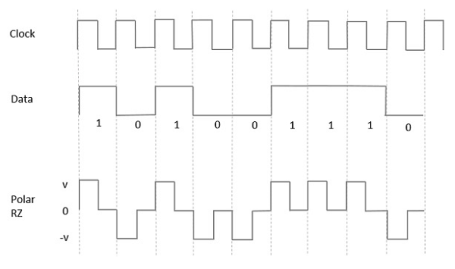
Fig 4 Polar RZ
Advantages
The advantages of Polar RZ are −
Disadvantages
The disadvantages of Polar RZ are −
Bipolar Signaling
This is an encoding technique which has three voltage levels namely +, - and 0. Such a signal is called as duo-binary signal.
An example of this type is Alternate Mark Inversion AMIAMI. For a 1, the voltage level gets a transition from + to – or from – to +, having alternate 1s to be of equal polarity. A 0 will have a zero-voltage level.
Even in this method, we have two types.
From the models so far discussed, we have learnt the difference between NRZ and RZ. It just goes in the same way here too. The following figure clearly depicts this.
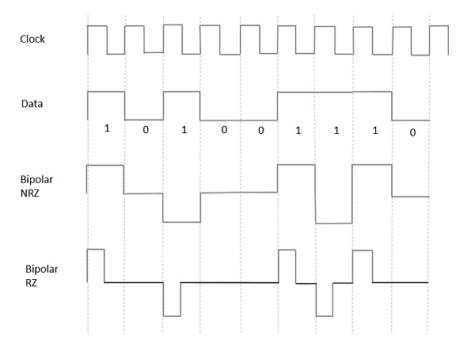
Fig 5 Bipolar RZ and Bipolar NRZ
The above figure has both the Bipolar NRZ and RZ waveforms. The pulse duration and symbol bit duration are equal in NRZ type, while the pulse duration is half of the symbol bit duration in RZ type.
Advantages
Following are the advantages −
Disadvantages
Following are the disadvantages −
Power Spectral Density
The function which describes how the power of a signal got distributed at various frequencies, in the frequency domain is called as Power Spectral Density PSD.
PSD is the Fourier Transform of Auto-Correlation Similarity between observations. It is in the form of a rectangular pulse.
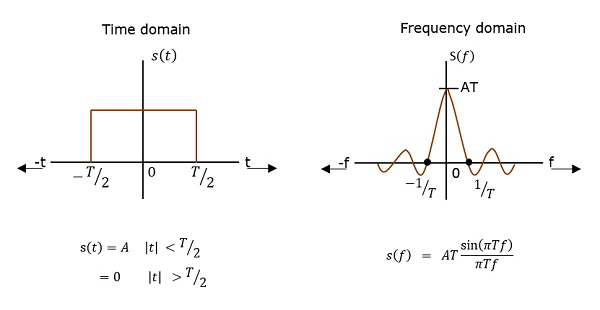
Fig 6 PSD
Key Takeaways:
Pulse code modulation is a method that is used to convert an analog signal into a digital signal so that a modified analog signal can be transmitted through the digital communication network. PCM is in binary form, so there will be only two possible states high and low (0 and 1). We can also get back our analog signal by demodulation. The Pulse Code Modulation process is done in three steps Sampling, Quantization, and Coding. There are two specific types of pulse code modulations such as differential pulse code modulation (DPCM) and adaptive differential pulse code modulation (ADPCM)
In Pulse Code Modulation, the message signal is represented by a sequence of coded pulses. This message signal is achieved by representing the signal in discrete form in both time and amplitude.
The transmitter section comprises of Sampling, Quantizing and Encoding. The low pass filter prior to sampling prevents aliasing of the message signal.
The basic operations in the receiver section are regeneration of impaired signals, decoding, and reconstruction of the quantized pulse train.
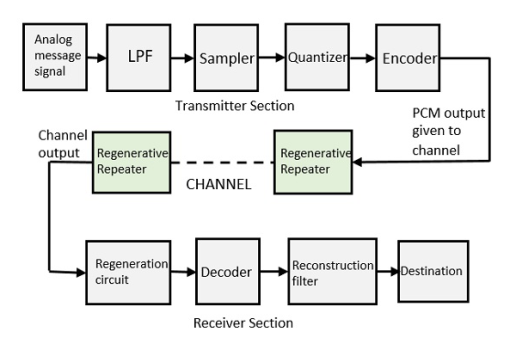
Fig.7: PCM
This filter eliminates the high frequency components present in the input analog signal to avoid aliasing of the message signal.
It helps to collect the sample data at instantaneous values of message signal, so as to reconstruct the original signal. The sampling rate must be in accordance with the sampling theorem.
It reduces excessive bits and confines the data. It reduces the redundant bits and compresses the value of the sampled output.
The digitization of analog signal is done by the encoder. It designates each quantized level by a binary code. Encoding minimizes the bandwidth used.
It increases the signal strength. The output of the channel also has one regenerative repeater circuit, to compensate the signal loss and reconstruct the signal, and also to increase its strength.
The decoder circuit decodes the pulse coded waveform to reproduce the original signal. This circuit acts as the demodulator.
After the digital-to-analog conversion is done by the regenerative circuit and the decoder, a low-pass filter is employed, called as the reconstruction filter to get back the original signal.
Hence, the Pulse Code Modulator circuit digitizes the given analog signal, codes it and samples it, and then transmits it in an analog form. This whole process is repeated in a reverse pattern to obtain the original signal.
Key takeaway
The transmitter section comprises of Sampling, Quantizing and Encoding. The low pass filter prior to sampling prevents aliasing of the message signal.
The basic operations in the receiver section are regeneration of impaired signals, decoding, and reconstruction of the quantized pulse train.
This is called as M-ary Phase Shift Keying M−ary PSK
The phase of the carrier signal, takes on M different levels.
Representation of M-ary PSK
Si(t)=√2E/T cos(wot +ϕit) 0≤t≤T and i=1,2...M
ϕi(t)=2πiM where i=1,2,3......M
Some prominent features of M-ary PSK are −
So far, we have discussed different modulation techniques. The output of all these techniques is a binary sequence, represented as 1s and 0s
Multi-level modulation techniques permit high data rates within fixed bandwidth constraints. A convenient set of signals for M-ary PSK is
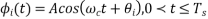
Where the M phase angles are

For equiprobable ones and zeros the PSD for M-ary PSK is

The symbols in this case are of duration  , so the information (or bit) rate
, so the information (or bit) rate  satisfies
satisfies
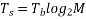
The potential bandwidth efficiency of M-ary PSK can be shown to be
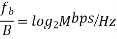
A phase diagram and signal constellation diagram for the case of M = 8 are shown below:
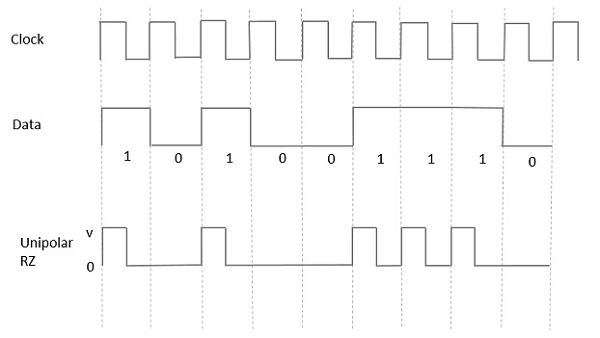
Fig 8 Phasor and Signal Constellation Diagram
The probability of error calculation involves analysing the received phase at the receiver, (in the presence of noise), and comparing it to the actual phases. An exact solution is difficult to compute, but for 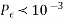 an approximate probability of making a symbol error is
an approximate probability of making a symbol error is

If a Gray code is used, then the corresponding bit error is approximately
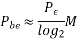
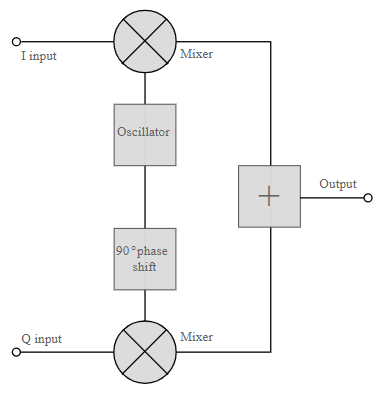
M-ary QAM
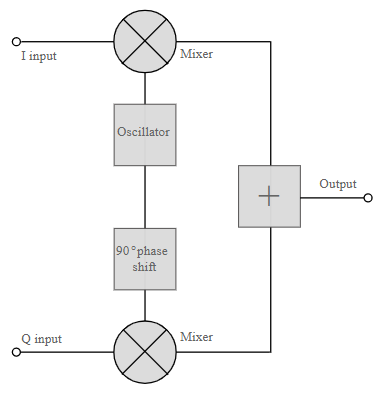
The QAM modulator essentially follows the idea that can be seen from the basic QAM theory where there are two carrier signals with a phase shift of 90° between them. These are then amplitude modulated with the two data streams known as the I or In-phase and the Q or quadrature data streams. These are generated in the baseband processing area.
Basic QAM I-Q modulator circuit
The two resultant signals are summed and then processed as required in the RF signal chain, typically converting them in frequency to the required final frequency and amplifying them as required.
Fig 9 QAM Modulator
It is worth noting that as the amplitude of the signal varies any RF amplifiers must be linear to preserve the integrity of the signal. Any non-linearities will alter the relative levels of the signals and alter the phase difference, thereby distorting he signal and introducing the possibility of data errors.
Basic QAM I-Q demodulator circuit
The basic modulator assumes that the two quadrature signals remain exactly in quadrature.
A further requirement is to derive a local oscillator signal for the demodulation that is exactly on the required frequency for the signal. Any frequency offset will be a change in the phase of the local oscillator signal with respect to the two double sideband suppressed carrier constituents of the overall signal.
Systems include circuitry for carrier recovery that often utilises a phase locked loop - some even have an inner and outer loop. Recovering the phase of the carrier is important otherwise the bit error rate for the data will be compromised.
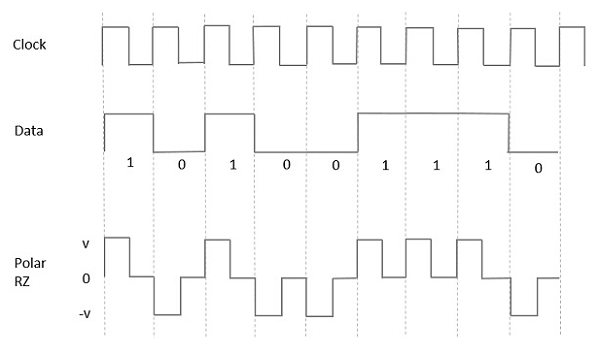
Fig 10 QAM Demodulator
The circuits shown above show the generic IQ QAM modulator and demodulator circuits that are used in a vast number of different areas. Not only are these circuits made from discrete components, but more commonly they are used within integrated circuits that are able to provide a large number of functions.
Error Probability
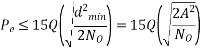
Key takeaway
The QAM modulator essentially follows the idea that can be seen from the basic QAM theory where there are two carrier signals with a phase shift of 90° between them. These are then amplitude modulated with the two data streams known as the I or In-phase and the Q or quadrature data streams.
The phase of the carrier signal, takes on M different levels.
Representation of M-ary PSK
Si(t)=√2E/T cos(wot +ϕit) 0≤t≤T and i=1,2...M
ϕi(t)=2πiM where i=1,2,3......M
Differential pulse code modulation (DPCM) is a procedure of converting an analog into a digital signal in which an analog signal is sampled and then the difference between the actual sample value and its predicted value (predicted value is based on previous sample or samples) is quantized and then encoded forming a digital value.
DPCM code words represent differences between samples unlike PCM where code words represented a sample value.
Basic concept of DPCM - coding a difference, is based on the fact that most source signals show significant correlation between successive samples so encoding uses redundancy in sample values which implies lower bit rate.
Realization of basic concept (described above) is based on a technique in which we have to predict current sample value based upon previous samples (or sample) and we have to encode the difference between actual value of sample and predicted value (the difference between samples can be interpreted as prediction error).
Because it's necessary to predict sample value DPCM is form of predictive coding.
DPCM compression depends on the prediction technique, well-conducted prediction techniques lead to good compression rates, in other cases DPCM could mean expansion comparing to regular PCM encoding.
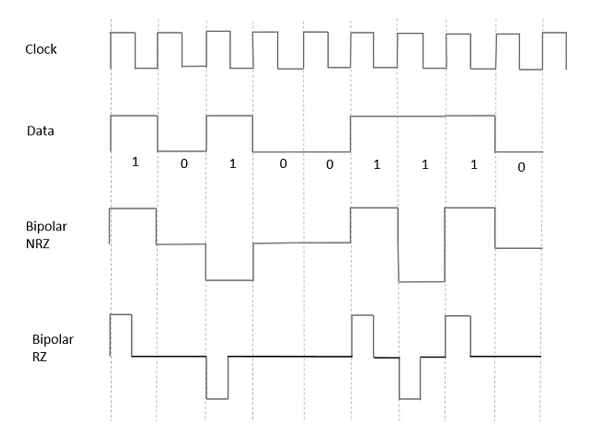
Fig.11: DPCM
Key Takeaways:
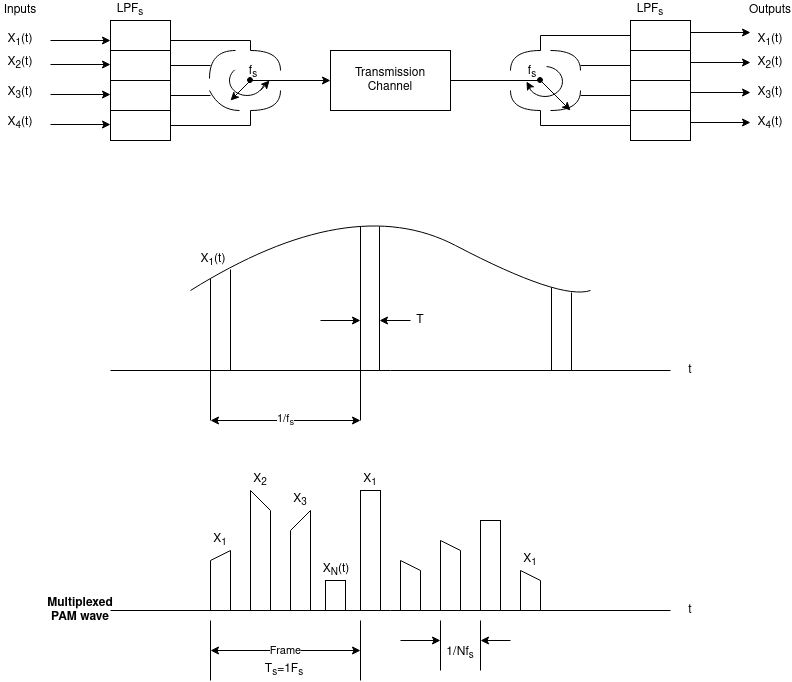
In pulse modulation the time division multiplexing makes the maximum utilisation of the transmission channel. The TDM can be analog or digital. The digital multiplexing is discussed below. The block diagram for TDM is shown below. N PAM channels are multiplexed and each channel to be transmitted is passed through the LPF. The input to the commutators is the signal coming out from the LPF. The commutator rotates at the rate of fs. A t the receiver the demodulator separates the time multiplexed input channels. These signal pass through the low-pass reconstruction filters. If W is the highest signal frequency then according to the sampling theorem fs 2W
2W

Fig 12 TDM system block diagram and waveform [Ref 6]
The time space between two samples is given by
Ts = 1/fs
Ts 2W
2W
If there are N input channels then the space between two samples is given by
Space between two samples = Ts/N
The number of pulses/secs are called as signalling rate of TDM denoted by r
r= Nfs
For PAM/TDM Signalling rate r 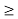 2NW
2NW
Synchronisation in TDM
There should always be synchronisation in transmitter and receiver. Usually, markers are inserted to indicate the separation between the frames. Synchronisation is obtained due to these marker pulses but the number of channels to be multiplexed is reduced by one. They become N-1.
Crosstalk
In TDM transmission the signal is converted to smooth modulating waveform when passed through the baseband filter. The baseband value passes through the values of all the individual samples.
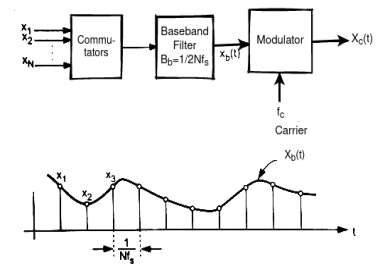
Fig 13 TDM transmission with baseband filtering and its waveform
Due to this baseband filter crosstalk arises in between two samples. This interference can be reduced by increasing the distance between individual signal samples. The minimum distance required to avoid crosstalk between two samples is called as guard time.
Fig 14 Applied rectangular pulse and its response
From above figure we see that even after the pulse is removed the response decays from its value A and then takes longer period. The guard time Tg represents minimum pulse spacing. After guard time end the pulse tail is less than Act.
Act = A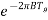
Key takeaway
The time space between two samples is given by
Ts = 1/fs
Ts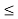 2W
2W
The number of pulses/secs are called as signalling rate of TDM denoted by r
r= Nfs
For PAM/TDM Signalling rate r 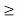 2NW
2NW
Example
Twelve different message signals each of bandwidth 20kHz are to be multiplexed and transmitted. Determine the minimum bandwidth required for PAM/TDM system?
Sol: No. of channels N =12
Bandwidth of each channel fm = 20kHz
Minimum bandwidth required to avoid crosstalk is = Nfm = 20 x 12 = 240kHz
The type of modulation, where the sampling rate is much higher and in which the step size after quantization is of a smaller value Δ, such a modulation is termed as delta modulation.
Delta Modulation is a simplified form of DPCM technique, also viewed as 1-bit DPCM scheme. As the sampling interval is reduced, the signal correlation will be higher.
Delta Modulator
The Delta Modulator comprises of a 1-bit quantizer and a delay circuit along with two summer circuits. Following is the block diagram of a delta modulator.

Fig.15: Delta Modulator
The predictor circuit in DPCM is replaced by a simple delay circuit in DM.
From the above diagram, we have the notations as −
Using these notations, now we shall try to figure out the process of delta modulation.
ep(nTs)=x(nTs)−xˆ(nTs) ---------equation 1
=x(nTs)−u([n−1]Ts
=x(nTs)−[xˆ[[n−1]Ts]+v[[n−1]Ts]] -------equation 2
Further,
v(nTs)=eq(nTs)=S.sig.[ep(nTs)] ---------equation 3
u(nTs)=xˆ(nTs)+eq(nTs)
Where,
Hence,
u(nTs)=u([n−1]Ts)+v(nTs) ---------equation 4
Which means,
The present input of the delay unit
= The previous output of the delay unit + the present quantizer output the present quantizer output
Assuming zero condition of Accumulation,
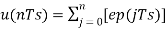
Accumulated version of DM output = 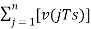 --------equation 5
--------equation 5
Now, note that
xˆ(nTs)=u([n−1]Ts)
=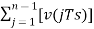 ---------equation 6
---------equation 6
Delay unit output is an Accumulator output lagging by one sample.
From equations 5 & 6, we get a possible structure for the demodulator.
A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta (Δ). The output quality of the waveform is moderate.
Delta Demodulator
The delta demodulator comprises of a low pass filter, a summer, and a delay circuit. The predictor circuit is eliminated here and hence no assumed input is given to the demodulator.
Following is the diagram for delta demodulator.
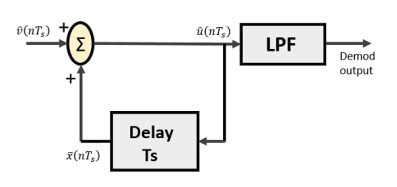
Fig.16 Delta Demodulator
From the above diagram, we have the notations as −
A binary sequence will be given as an input to the demodulator. The stair-case approximated output is given to the LPF.
Low pass filter is used for many reasons, but the prominent reason is noise elimination for out-of-band signals. The step-size error that may occur at the transmitter is called granular noise, which is eliminated here. If there is no noise present, then the modulator output equals the demodulator input.
Key takeaway
The type of modulation, where the sampling rate is much higher and in which the step size after quantization is of a smaller value Δ, such a modulation is termed as delta modulation.
Delta modulation is subject to rate of rise over load problems whenever the input changes too rapidly for the stepped wave form to follow it. If the input signal level remains constant, the reconstructed Delta modulation waveform exhibits a hunting behaviour known as idling noise. This idling noise is a square wave at one half the clock rate. If the clock rate is much greater than twice the highest frequency in the input signal, most of the idling noise can be filtered out at the receiver.
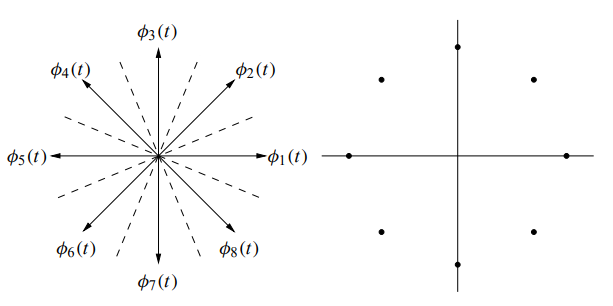
Fig 17 Slope Overload
Slope Overload: Slope overload distortion occurs when the analog input signal changes at a faster rate than the DAC can maintain it, the slope of the analog signal is greater than the delta modulator can maintain. In general, when the slope of stair case is less than (or) equal to modulating signal, the slope overloading occurs. Increasing the clock frequency reduces the probability of slope overload occurring. General method to reduce the slope overload is to increase the magnitude of the size. Assume the input for Delta modulation be f(t) = A cos ωmt.
If the step size used in the Delta modulation system is ‘Δ’, then the maximum (rate of rise) slope over load is / Ts
Granular noise: In general, Granular noise occurs
There is a need to have a large step size to accommodate a wide dynamic range, whereas small step size is required for the accurate representation of relatively low-level signals.
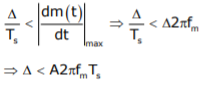
Therefore, a granular noise can be removed by taking a small resolution of step size and a slope over load distortion can be removed by taking a large resolution.
Key takeaway
The input for Delta modulation be f(t) = A cos ωmt.
In digital modulation, we have come across certain problem of determining the step-size, which influences the quality of the output wave.
A larger step-size is needed in the steep slope of modulating signal and a smaller step size is needed where the message has a small slope. The minute details get missed in the process. So, it would be better if we can control the adjustment of step-size, according to our requirement in order to obtain the sampling in a desired fashion. This is the concept of Adaptive Delta Modulation.
Following is the block diagram of Adaptive delta modulator.
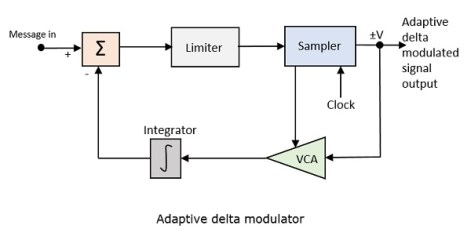
Fig. 18 Adaptive delta modulator
The gain of the voltage-controlled amplifier is adjusted by the output signal from the sampler. The amplifier gain determines the step-size and both are proportional.
ADM quantizes the difference between the value of the current sample and the predicted value of the next sample. It uses a variable step height to predict the next values, for the faithful reproduction of the fast-varying values.
Key takeaway
ADM quantizes the difference between the value of the current sample and the predicted value of the next sample. It uses a variable step height to predict the next values
Adaptive Differential Pulse Code Modulation (ADPCM), also called Delta Pulse Code Modulation, is a compression coding for a signal, which is based on differential values similar to Differential Pulse Code Modulation (DPCM), and in which the scaling of the quantization stages is additionally adjusted (adapted) depending on the signal curve.
ADPCM is a pulse code modulation with prediction function. When the signal is processed, an attempt is made to predict the further course of the signal within the next section. For the quantization of the signal in the next time step only the difference between predicted and real signal is used. Due to this difference formation, fewer bits can be used to describe the signal.
With this method, both the prediction function and the quantization level are "adapted" anew with each work step. This control loop provides a better signal prediction than DPCM.
References
1. “Communication Systems”, Simon Haykin, Wiley publication, 4th Edition, 2004
2. “Digital Communication Fundamentals and Applications”, Bernard Sklar, Pearson Education India, 2nd Edition, 2009
3. “Modern Electronic Communication”, Miller Gary M, Prentice-Hall, 6th Edition, 1999
4. “Digital Communications”, John Proakis, Tata Mc Graw Hill, 5th Edition, 2007
5. “Electronic Communication Systems, Fundamentals Through Advanced”, Wayne Tomsi, Pearson Education, 4th Edition, 2001
6. Digital Communication, J.S.Chitode,3rd Edition ,Technical Publication.
