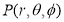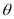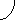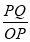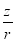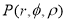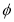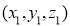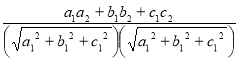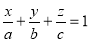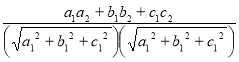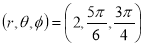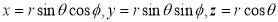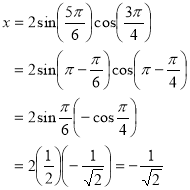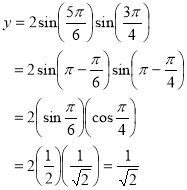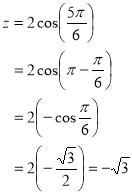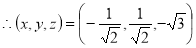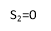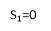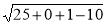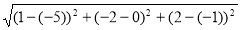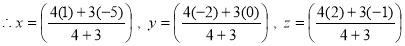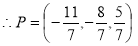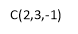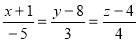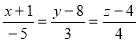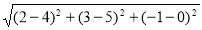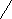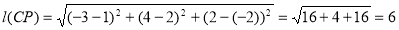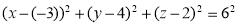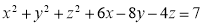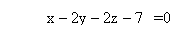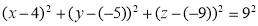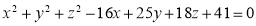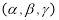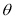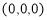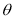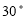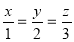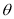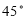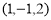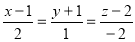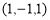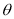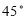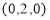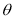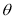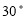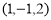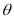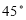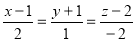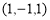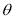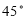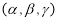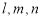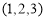Unit-5
Solid Geometry
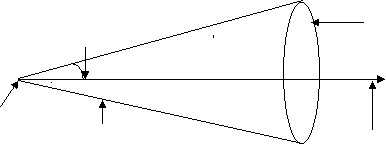
P(x,y,z)
O Y
M X
|
M Q X
Z =r cos From right angled triangle OQP, In ONQ cos =
In OMQ, sin =
|
N Q Y Cos = O M = x = cos Sin = y = sin z = z Preliminaries Distance Formula: Distance between two points, P(x, y, z,) and Q(x2, y2, z2)
PQ = Direction Cosines : If a line OP makes an angle , and with X, Y and Z axes respectively then the quantities cos , cos , cos are called direction cosines (d. c. s) of line OP, where O is the origin.Direction cosines of line are denoted by l, m, n Direction ratios : Numbers a, b, c which are proportional to direction cosines l, m, n respectively are called direction ratios of given line. We can prove that l = , m = , n =
(x1 – x2, y1 – y2, z1 – z2) are d. r.’s of line joining the points
Angle between two lines : If l1, m, n and l2, m2, n2 are d. c. s of two line and if is angle between those two lines then cos = Equation of Plane : (1) General form :Ifa,b,c are direction ratios of normal to plane then equation of plane is ax + by + cz + d = 0
(2) Intercept form :If plane intersects with co-ordinate axes at a,b,c thenequation of plane is
(3) Normal (perpendicular) form : If l, m, n are d. c.s of normal to plane and p is perpendicular distance from origin to the plane, then Normal form of plane is, l x + my + nz = p
(4) Angle between two planes :
Angle between two planes :a1 x + b1 y + c1 z + d1 = 0 and a2x + b2 y + c2 z + d2 = 0
is given by cos = Length of Perpendicular : Perpendicular distance from the point P(x1, y1, z1) to the plane ax + by + cz + d = 0 is
|
Ex1) Find the Cartesian co-ordinates of a pointe whose spherical polar co-ordinates are
(2, , )
Sol)
Given |
We know that |
|
|
|
|
Ex2) Find the spherical polar co-ordinates of a the points whose Cartesian co-ordinates are
(i) (3, 4, 5) (ii) (– 1, 1, – 1)
Ex 3: Findthe cylindrical co-ordinates of the point whose Cartesian co-ordinates are (– 3, 4, 12)
Ex4) Find (i)Spherical polar (ii) cylindrical equation of surfaces whose Cartesian equations are
(a)x2 + y2 = a2 (b) x2 + y2 + z2 = 16.
5.4 Sphere:
Definition :
The locus of a point which moves in space such that it remains at a constant distance from a fixed point defines a spherical surface or a sphere. The fixed point is called the centre of the sphere and the constant distance is called the radius.
Equation of Sphere :
a) Centre – radius form :
Let P (x, y, z) be any point on sphere and C (a, b, c) be centre and r be radius then by distance formula the equation of sphere is
(x – a)2 + (y – b)2 + (z – c)2=r2 …(1)
Note : If centre of sphere is (0, 0, 0) then its equation is given by x2 + y2 + z2 = r2
(b) General form :
Equation(1) can be simplified as
x2 + y2 + z2 + 2ux + 2vy + 2wz + k = 0 where 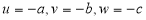 and
and
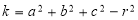
This is general equation of sphere.
Centre of sphere is (– u, – v, – w) and radius =
(c) Diameter form :If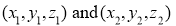 are end points of diameter of sphere then
are end points of diameter of sphere then
equation of sphere is
(x – x1) (x – x2) + (y – y1) (y – y2) + (z – z1) (z – z2)=0
Ex1) Find the equation of sphere passing through the points (1 ,3 ,1 ), (2 ,- 1 ,1 ), (1 ,2 ,0 ), (1 ,- 1 ,1 ).
Sol)
Let the equation of sphere be |
x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0……………(1) |
Since, sphere pass through the point ( 1,3,1),therefore from equation ( 1 ), we get |
|
1 + 9 + 1 + 2u+6v+2w+d=0 2u+6v+2w+d= - 11.........(2) |
Since, sphere pass through the point ( 2,-1,1),therefore from equation ( 1 ), we get |
4 + 1 + 1 + 4u-2v+2w+d=0 4u-2v+2w+d= - 6............(3) |
Since, sphere pass through the point ( 1,2,0),therefore from equation ( 1 ), we get |
1 + 4 + 0 + 2u+4v+0+d=0 2u+4v+d= - 5............(4) |
Since, sphere pass through the point ( 1,-1,1),therefore from equation ( 1 ), we get |
1 + 1 + 1 + 2u-2v+2w+d=0 2u-2v+2w+d= - 3............(5) |
Eq(2) - Eq(3) gives - 2u + 8v = - 5 ........(6) |
Eq(2) – Eq(4) gives 2v + 2w = - 6.......(7) |
Eq.(2)-Eq(5) gives 8v = - 8 v = -1 |
Using value of v in equation (6) we get u = - 3/2 |
Using value of v in equation (7) we get w = - 2 |
Using values of u,v,w in equation(2) we get d = 2 |
From equation(1), we get x2 + y2 + z2 + 2(-3/2)x + 2(-1)y + 2(-2)z + 2 = 0 |
x2 + y2 + z2 - 3x - 2y - 4z + 2 = 0 |
Ex2) Find the equation of sphere which passes through origin and makes equal intercepts of unit length on the axes.
Sol)
Let equation of spherebe x2 + y2 + z2 + 2ux + 2vy + 2wz + d=0……………(1) |
d = 0 ( sphere pass through origin) |
Since sphere intersect at 1 on x-axis i.e. sphere intersects-axis at the point (1 , 0 ,0 ) |
|
u = – |
Similarly, v = – (sphere intersect y-axis at the point ( 0 ,1 ,0 ) |
, w = – (sphere intersect z-axis at the point ( 0 ,0 ,1 ) |
Using values of u,v,w and d in equation(1) ,we get |
x2 + y2 + z2 – x – y – z = 0 |
|
Ex.3: Prove that the spheres |
x2 + y2 + z2 – 2x + 4y – 4z = 0 and x2 + y2 + z2 + 10 x + 2z + 10 = 0 |
touch each other. Find the co-ordinates of point of contact. |
Soln. : |
|
|
|
|
|
|
|
|
Let S1 = x2 + y2 + z2 – 2x + 4y – 4z = 0 |
Centre c1 = (1, – 2, 2) |
Radium, r1 = = 3 |
S2 = x2 + y2 + z2 + 10x + 2z + 10 = 0 |
Centre, c2 = (– 5, 0, – 1) |
Radius, r2 = |
Now d (C1 C2) = |
= = = 7 |
r1 + r2 = 3 + 4 = 7 |
ie distance between centers of two sphere is equal to sum of radii therefore the spheres touches each other externally. |
Let P be the point of contact. We observe that P divides join of C1C2 in the ratio 4:3 |
|
|
Ex4) Find the equation of sphere which has its centre at (2, 3, –1) and touches the line 
Sol:
|
|
|
|
|
|
|
|
|
Equation of line is given in symmetrical form. |
The co-ordinates of any point on line are given by, |
|
x = – 5k – 1, y = 3k + 8, z = 4k + 4 |
The co-ordinates of any point on this line are of the form x = – 5k – 1, y = 3k + 8, z = 4k + 4 |
Let these are co-ordinates of point P P (– 5 k – 1, 3k + 8, 4k + 4)………(1) |
Direction ratios of OP are (– 5k –3, 3k + 5, 4k + 5)…( |
Also d. r.s of given line are (– 5, 3, 4) |
If P is point of contact, OP is perpendicular to given line |
–5 (– 5k – 3) + 3 (3k + 5) + 4 (4k + 5) = 0 |
|
50k + 50 = 0 k = – 1 |
co-ordinates of P (4, 5, 0) ( |
OP = radius of sphere = |
OP = = 3 |
By using centre-radius form, |
(x – 2)2 + (y – 3)2 + (z + 1)2 = 9 |
x2 + y2 + z2 – 4x – 6y + 2z + 5 = 0 |
Ex5) Find the equation of sphere touching three co-ordinate planesand the plane 2x + y + 2z = 6.
Sol)
Let the equation of sphere be x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0……………(1) |
Co-ordinates of center of sphere are ( -u , -v,-w) |
The equations of co-ordinates planes x = 0, y = 0, z = 0. |
The length of perpendicular from centre of sphere to these planes is equal to radius of sphere. |
= = = ( |
from point on given plane) |
We have u = v = w ( |
From last two ratios, |
u = |
5u + 6 = 3u |
u = - 3 |
(– u, – v, – w) = (3, 3, 3) ( u = v = w) |
radius = x-co-ordinate of center of sphere = - u = 3 |
Equation of sphere |
(x – 3)2 + (y – 3)2 + (z – 3)2 = 9 |
x2 + y2 + z2 – 6x – 6y – 6z + 18 = 0 |
Ex6) A sphere of constant radius r passes through the origin and cuts the axes in A, B, C. Prove that the locus foot of perpendicular from origin to the plane ABC is given by
(x2 + y2 + z2) (+ + ) = 4r2.
Sol)
Let sphere passes through origin and intercepts co-ordinate axes at say |
A(x1,0,0),B(0,y1,0),C(0,0,z1) |
Equation of sphere is given by |
x2 + y2 + z2 – x1x – y1y – z1z = 0 |
Center of sphere is ( x1,y1,z1) |
Radiaus = = r (given) |
+ + = 4r2 …(1) |
Now equation plane cutting axes at A, B, C is |
+ + = 1 …(2) |
Let (, , ) be foot of perpendicular from origin to the plane ABC (locus point). |
drs of OP , , |
drs of PQ x – , y – , z – |
OP is normal to plane OP PQ |
(x – ) + (y – ) + (z – ) = 0 |
x + y + z = + + = M (say) |
x + y+ z = M |
+ + = 1 …(3) |
Comparing Equation (2) and (3) we get, |
x1 = , y1 = , z1 = |
Equation (1) |
+ + = 4r2 |
( + + )2= 4r2 |
i.e. ( + + )2 ( + + ) = 4r2 |
|
Sphere:Tangent plane
A plane say 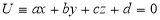 touching given sphere say
touching given sphere say  in only one point is called as tangent plane of given sphere
in only one point is called as tangent plane of given sphere
|
Tangent plane Property:
When a plane touch given sphere then length of perpendicular from centre of sphere to plane is equal to radius of sphere.
Ex1) Find the equation of sphere which passes through the point (1, 0, 0) and touchesthe plane 2x – y – 2z – 4 = 0 at the point (1, 2, – 2).
Sol)
|
|
|
|
|
2x – y – 2z – 4 = 0 |
|
|
Let C be center of sphere and let sphere touch the plane 2x – y – 2z – 4 = 0 at the point |
Say P(1, 2, – 2) |
Line CP is normal to plane 2x – y – 2z – 4 = 0 therefore d,r,’s of line CP are 2,-1,2. |
Line CP passing through point P(1, 2, – 2) |
|
x = 2k + 1,y = - k +2,z = - 2k-2 |
The co-ordinates of any point on this line are of the form x = 2k + 1,y = - k +2,z = - 2k-2 |
Let these are co-ordinates of point center C of sphere |
C (2k+ 1, –k + 2, – 2k – 2) |
we have CP2 = CQ2 |
(2k + 1– 1)2 + (– k + 2 – 0)2 + (– 2k – 2 – 0)2 |
|
|
|
4k = – 8 |
|
co-ordinates of center of sphere is C( -3,4,2) |
Radius of sphere = |
Equation of sphere by using center-radius form is given by |
|
|
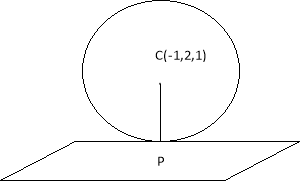
Ex2) Prove that the sphere x2 + y2 + z2 + 2x – 4y – 2z – 3 = 0 touch the plane
2x – 2y + z + 14 = 0 and find the co-ordinates of point of contact.
Sol)
Let S x2 + y2 + z2 + 2x – 4y – 2z – 3 = 0 |
V 2x – 2y + z + 14 = 0 |
|
|
|
|
|
|
|
|
|
|
|
Co-ordinates of centre of sphere C (– 1, 2, 1) |
Radius of sphere = = 3 |
l (CP) = Perpendicular from C(– 1, 2, 1) on the plane 2x – 2y + z + 14 = 0 |
= |
= |
= 3 |
Length of Perpendicular from centre of sphere on plane equal to radius of sphere therefore given sphere touch the plane |
To find the Point of Contact : |
Equation of line CP passing through the point C(– 1, 2, 1) and with dr’s 2, – 2, 1 is given by |
= = |
= = = t say |
x = 2t – 1, y = – 2t + 2, z = t + 1 |
These are co-ordinates of any general point on line CP. |
Let these are co-ordinates of point P. |
ie P P (2t – 1, – 2 t + 2, t + 1) |
As P lies on given plane U = 0 |
ie on 2x – 2y + z + 14 = 0 |
2 (2t – 1) – 2 (– 2 t + 2) + (t + 1) + 14 = 0 |
4t – 2 + 4t – 4 + t + 1 + 14 = 0 |
9t + 9 = 0 t = –1 |
P = P (– 2 – 1, 2 + 2, –1 + 1) |
= P (– 3, 4, 0) |
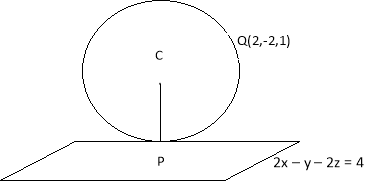
Ex3) Find the equation of sphere which passes through the point (2, – 2, 1) and touches the
plane 2x – y – 2z = 4 at (1, 2, – 2)
Sol)
|
|
|
|
|
|
|
|
|
|
Line CP is normal to the plane 2x – y – 2z = 4 |
dr’s of CP are 2, –1, 2 |
Line CP pass through the point P (1, 2, – 2) |
Equation of line CP is |
= = = t say |
x = 2t + 1, y = – t + 2, z = 2t – 2 |
Let these are co-ordinates of point C |
C C (2t + 1, – t + 2, 2t – 2) |
Now l (CP) = l (CA)= |
= |
= |
9t2 = 9t2 – 24 t + 26 |
24 t = 26 |
t = |
C |
C |
Radius of sphere = l (CP) |
= |
= |
= |
l (CP) = |
Equation of sphere by centre-radius form is given by |
+ + = |
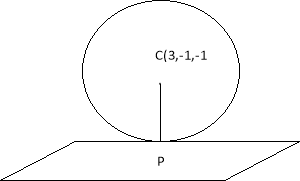
Ex4) Find the equation of sphere tangential to the plane x – 2y – 2z = 7 at (3, – 1, – 1) and passing through the point (1, 1, – 3).
Sol)
|
|
|
|
|
|
|
|
|
|
Line CP is normal to plane |
x – 2y – 2z – 7 = 0 |
drs of CP are 1, – 2, –2. |
line CP passing through the point (1, 1, – 3) |
Equation of line CP is given by |
= = = t say |
x = t + 1, y = – 2t + 1, z = – 2t – 3 |
Let, C C (t + 1, – 2t + 1, – 2t – 3) |
Since, l(CP) = l(CA) (Both are radius of sphere) |
= |
= |
Squaring on both sides |
9t2 = (t2 – 4t + 4) + (4t2 – 8t + 4) + (4t2 + 8t + 4) |
9t2 = 9t2 – 4t + 12 |
4t = 12 t = 3 |
C (4, – 5, – 9) |
Radius of sphere = l (CP) |
= |
= = 9 |
Equation of sphere by using center-radius form is given by |
|
|
Section of a sphere by a plane,Orthogonal sphere
|
Let the equation of sphere be x2 + y2 + z2 +2ux + 2vy + 2wz + d = 0. And the equation of plane be
U lx + my + nz – p = 0
lx + my + nz – p = 0
If a plane lx + my + nz – p = 0 cuts the sphere x2 + y2 + z2 +2ux + 2vy + 2wz + d = 0.
The section obtained is a circle for this we show that PQ is constant and P is fiexd.
From Fig. CQ is radius of sphere (fixed)
For a given plane and sphere the foot of perpendicular from centre is fixed.
P is fixed point.
From right angled triangle CPQ.
CP2 + PO2 = CQ2
PQ =
=
 PQ = Constant
PQ = Constant
Thus the locus is a circle.
Intersection of two spheres :
The curve of intersection of two sphere is a circle.
Equation of circle :
The common section of a sphere and a plane represents a circle. Therefore equation of sphere and plane together represents a circle.
Thus if S = 0 is equation of sphere and U = 0 is equation of plane, the equations
S = 0 and U = 0 together represents a circle.
Similarly two sphere S1 = 0, S2 = 0 also represents equation of circle.
Note :
(1) In three dimensional geometry circle is represented by the combination of two equations. i.e. S = 0, U = 0.
(2) The equation of sphere passing through the circle which is section of sphere
S = x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0 and plane U = ax + by + cz + d = 0 is given by
S + U = 0.
(3) For different values of we get different spheres passing through given circle.
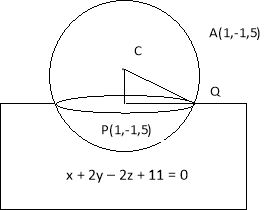
Ex1) Find the equation of sphere which passes through the point (6, 4, 3) and meets the plane
x + 2y – 2z + 11 = 0 in a circle of radius 4 units with centre at (1, – 1, 5)
Sol)
|
|
Here we find co-ordinates of centre of sphere then by using centre – radius form we find equation of sphere. |
Given circle is section of required sphere taken by plane x + 2y – 2z + 11 = 0 |
Centre of this circle is P (1, – 1, 5) |
Radius of circle say l (PQ) = 4 |
Line CP is normal to plane x + 2y – 2z + 11 = 0 |
dr’s of line CP are 1, 2, – 2 |
Line CP pass through point P (1, –1, 5) |
Equation of line CP are |
= = = t say |
x = t + 1, y = 2t – 1, z = – 2t + 5 |
Let c (t + 1, 2t – 1, – 2t + 5) … (1) |
Now from right angle triangle CPQ, |
l (CP)2 + l (PQ)2 = l (CQ)2 |
[(t + 1) – 1]2 + [(2t – 1) + 1]2 + [(– 2t + 5) – 5]2 + 42 = l (CQ)2 |
9t2 + 16 = l (CQ)2 … (2) |
We have l (CQ) = l (CA) (∵ Radius of sphere) |
lCQ = lCA |
9t2 + 16 = [(t + 1) – 6]2 + [(2t – 1) – 4]2 + [(– 2t + 5) – 3]2 |
= (t – 5)2 + (2t – 5)2 + (– 2t + 2)2 |
= (t2 – 10t + 25) + (4t2 – 20t + 25) + (4t2 – 8t + 4) |
9t2 + 16 = 9t2 – 38 t + 54 |
38 t = 38 t = 1 |
From equation (1) |
C (2, 1, 3) which is centre of sphere |
l (CQ)2 = 9 + 16 = 25 ( from equation (2)) |
lCQ Which is radius of sphere |
Equation of sphere by using centre-radius form is |
(x – 2)2 + (y – 1)2 + (z – 3)2 = 25 |
x2 + y2 + z2 – 4x – 2y – 6z – 11 = 0 |
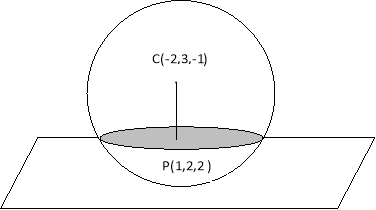
Ex2) Obtain equation of circle lying on the sphere x2 + y2 + z2 + 4x – 6y + 2z – 10 = 0 and having its centre at (1, 2, 2)
Sol)
Let S x2 + y2 + z2 + 4x – 6y + 2z – 10 = 0 |
Here we find equation of plane by which section of sphere S = 0 is taken co-ordinates of centre of sphere are C (– 2, 3, –1) |
|
|
|
|
|
|
|
|
|
|
|
|
Line CP is normal to required plane and line CP pass through the points P (1, 2, 2) and C– 2, 3, – 1 |
dr’s of line CP are 1 – (– 2), 2 – 3, 2 – (– 1) ie 3, – 1, 3 |
Equation of plane to which line CP is normal is of the form 3x – y + 3z + d = 0 … (1) |
But point P (1, 2, 3) lies on plane given by equation (1) |
3(1) – (2) + 3(2) + d = 0 |
d = 7 |
From equation (1), 3x – y + 3z + 7 = 0 |
Required equation of circle is |
x2 + y2 + z2 + 4x – 6y + 2z – 10 = 0 ; 3x – y + 3z + 7 = 0 |
Orthogonal Sphere :



The spheres are said to be intersect each other orthogonally if the tangent planes at their point of contact intersect each other at right angles.
If the tangent planes to the two spheres intersects at right angle. Implies that the normals at the point of contact to the two planes are also perpendicular to each other.
|
Let S1 = 0 and S2 = 0 be two spheres with Centers at C1 and C2 respectively
Where S1 = x2 + y2 + z2 + 2u1 x + 2v1 y + 2w1 z + d1 = 0
S2 = x2 + y2 + z2 + 2u2 x + 2v2 y + 2w2 z + d2 = 0
From Fig, (C1C2)2 = (PC1)2 + (PC2)2
(– u1 + u2)2 + (– v1 + v2)2 + (– w1 + w2)2
= (+ + – d1) + (+ + – d2)
– 2u1 u2 – 2v1v2 – 2w1 w2 = – d1 – d2
 2u1 u2 + 2v1 v2 + 2w1 w2 = d1 + d2
2u1 u2 + 2v1 v2 + 2w1 w2 = d1 + d2
This is condition for two spheres to be orthogonal
Ex1) Prove that two spheres
x2 + y2 + z2 + 6y + 4 = 0 x
x2 + y2 + z2 + 6x + 8y + 4z + 20 = 0 intersect each other orthogonally.
Sol)
Here u1 = 0, v1 = - 3, w1 = 0, d1 = 4
u2 = - 3, v2 = - 4, w2 = - 2, d2 = 20
Now 2 u1 u2 + 2v1 v2 + 2w1 w2 = 2 (0)(- 3) + 2(-3)(- 4) + 2(0)(- 2) = 24
Also d1 + d2 = 4 + 20 = 24
Given spheres intersects orthogonally.
Ex2) Find the equation of sphere that passes through the circle
x2 + y2 + z2 – 2x + 3y – 4z + 6 = 0 and
3x – 4y + 5z – 15 = 0 and cuts the sphere
x2 + y2 + z2 + 2x + 4y – 6z + 11 = 0 orthogonally.
Sol)
Equation of required sphere passing through given circle is |
(x2 + y2 + z2) – 2x + 3y – 4z + 6 + (3x – 4y + 5z – 15) = 0 … (1) |
x2 + y2 + z2 + (– 2 + 3) x + (3 – 4) y + (– 4 + 5) z + (6 – 15) = 0 |
Here u1 = (– 2 + 3), v1 = (3 – 4), w1 = (– 4 + 5) |
d1 = 6 – 15 |
For given sphere x2 + y2 + z2 + 2x + 4y – 6z + 11 = 0 … (2) |
u2 = 1, v2 = 2, w2 = – 3, d2 = 11 |
By given condition ie sphere given by equation (1) cuts the sphere given by (2) orthogonally. |
(– 2 + 3) + 2(3 – 4) – 3 (– 4 + 5) = (6 – 15) + 11 |
= – |
Put value of in equation (1) we get 5(x2 + y2 + z2) – 13x + 19y – 25z + 45 = 0 |
Sphere: Orthogonal sphere, Great circle |
NOTES:
Ex3) Find the equation of sphere through the circle x2 + y2 + z2 = 4 ; z = 4 and cutting the sphere x2 + y2 + z2 + 10y – 4z – 8 = 0 orthogonally,
Sol)
Equation of sphere passing through given circle x2 + y2 + z2 = 4 ; z = 4 is given by |
(x2 + y2 + z2 – 4) + (z – 4) = 0 … (1) |
x2 + y2 + z2 + z + (– 4 – 4) = 0 … (2) |
Here u1 = 0, v1 = 0, w1 = , d1 = – 4 – 4 |
Given sphere is S1 = x2 + y2 + z2 + 10y – 4z – 8 = 0 … (2) |
Here U2 = 0, v2 = 5, w2 = – 2, d2 = – 8 |
As spheres given by equation (1) cuts the sphere (2) orthogonally we have |
2u1u2 + 2v1v2 + w1w2 = d1+ d2 |
2 (0) (0) + 2 (0) (5) + 2 (– 2) = (– 4 – 4) – 8 |
– 2 = – 4 – 12 |
2 = – 12 |
= – 6 |
Using value of in equation (1) we get |
(x2 + y2 + z2) – 6 (z – 4) = 0 |
x2 + y2 + z2 – 6z + 8 = 0 |
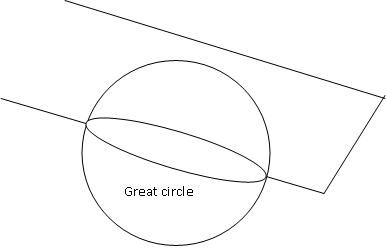
Great Circle :
|
We know that section of sphere S º x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0 by a plane U º ax + by + cz + d is a circle.
Section of sphere by plane at different position gives circles with different radii. A circle obtained by section of sphere by plane passing through centre of sphere is a circle with maximum radius which is called as great circle.
Note :
(1) Centre and radius of great circle and sphere is same.
(2) Co-ordinates of centre of sphere satisfies equation of plane
Ex1) Find the equation of sphere for which the circle x2 + y2 + z2 + 7y – 2z + 2 = 0 ; 2x + 3y + 4z = 8 is a great circle
Sol)
Equation of sphere passing through given circle is |
(x2 + y2 + z2 + 7y – 2z + 2) + (2x + 3y + 4z – 8) = 0 … (1) |
x2 + y2 + z2 + 2x + (7 + 3) y + (– 2 + 4) 2 + (2 – 8) = 0 |
Centre of this sphere is given by |
C |
Since given circle is a great circle of the |
Sphere x2 + y2 + z2 + 7y – 2z + 2 = 0 |
co-ordinates of centre of sphere satisfies equation of plane 2x + 3y + 4z = 8 |
2 [– ] + 3 + 4 = 8 |
– 2 – – + 4 – 8 |
= –1 |
Using value of in equation (1) we get |
(x2 + y2 + z2 + 7y – 2z + 2) – 1 (2x + 3y + 4z – 8) = 0 |
x2 + y2 + z2 – 2x + 4y – 6z + 10 = 0 |
Ex2) A sphere S has points (1, –2, 3) and (4, 0, 6) as opposite ends of diameter. Find the equation of the sphere having the intersection of S with the plane x + y – 2z + b = 0 as its great circle.
Sol) :
Equation of sphere by diameter form is given by, |
(x – 1) (x – 4) (y + 2) (y – 0) + (z – 3) (z – 6) = 0 |
ie x2 + y2 + z2 – 5x + 2y – 9z + 2z = 0 … (1) |
The intersection of the sphere (1) by a plane x + y – 2z + 6 = 0 is given by, |
(x2 + y2 + z2 – 5x + 2y – 9z + 22) + (x + y – 2z + 6) = 0 |
x2 + y2 + z2 + (– 5 + ) x + (2 + ) y + (– 9 – 2) z + 22 + 6 = 0 |
Centre of this sphere is |
Since given circle is great circle, this centre must lie on given plane x + 2y – 2z + 6 = 0 |
+ 2 – 2 + 6 = 0 |
= |
Equation of required sphere is, |
2 (x2 + y2 + z2) – 11x + 3y – 16 z + 38 = 0 |
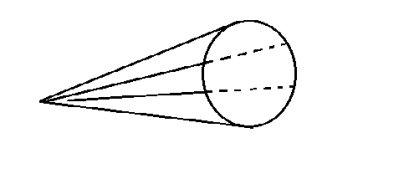
5.5 Cone
Introduction of cone, Right Circular Cone
NOTES:
Cone is a solid surface generated by a straight lines passing through fixed point and satisfying certain condition.
|
Type I: Equation of cone with vertex at origin
Ex1) Find the equation of cone whose vertex is at origin and guiding curve is given by
+ = 1 and z = c
Sol)
In above, equation + = 1 |
L.H.S. is of degree 2 but r.h.s. is of degree zero. |
By z = c we have = 1 |
= 1 |
|
+ = |
+ – = 0 |
|
is required equation of cone |
Ex2) Find the equation of cone whose vertex is at origin and guiding curve is given by
x2 – 2y2 + 3z2 = 4x + 9, x + y – z = 4.
Sol).
we have = 1
i.e. = 1
x2 – 2y2 + 3z2 – 4x – 9 = 0
Ex3) Find the equation of cone whose vertex is at origin and guiding curve is given by the plane
+ + = 1 meets the co-ordinate axes in A,B,C. Prove that the equation of cone generated by lines drawn from O to meet the circle ABC is yz + zx + xy = 0
Sol)
Given plane + + = 1 ents |
Co-ordinate planes at a, b, c respectively. Equation of sphere OABL is given by plane and a sphere. |
x2 + y2 + z2 – ax – by – cz = 0 |
we make this equation homogeneous, |
as x2 + y2 + z2 – (ax + by + cz) = 0 |
simplifying we get, |
|
|
Type II: Equation of cone with vertex other than origin |
Ex4) Find the equation of cane with vertex (3,1,2) and guiding curve2x2 + 3y2 = 1 and z = 0
Sol) :
The equation of any generator of cone with vertex at (3,1,2) is, |
|
From given equation z =0 |
= = |
x = 3 – , y = 1 – |
If this point has to be on the guiding curve ther it should satisfy 2x2 + 3 y2 = 1 |
i.e. 2 + 3 = 1 (2) |
we eliminate l, m, n from equation (2) |
from equation (1) |
x – 3 = (z – 2) = |
y – 1 = (z – 2) = |
From equation (2), |
2 + 3 = 1 |
2 = (z – 2)2 |
2+ 3 = (z – 2)2 |
2 + 3 = z2 – 4z + 4 |
8 x2 + 12y2 + 20z2 – 24xz – 12yz + 4z – 4 = 0 |
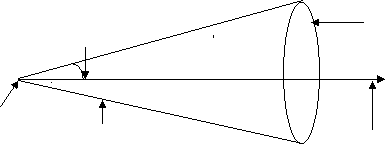
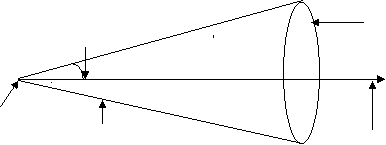
Right Circular Cone :
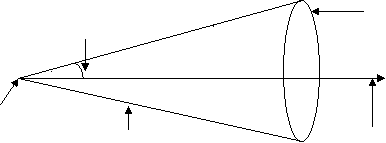
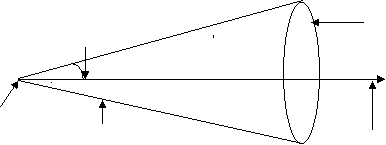
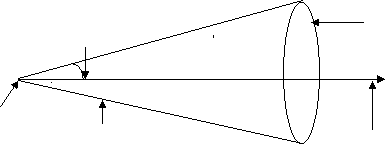
Right circular cone is a solid surface generated by st. line passing through fixed point and makes a constant angle with fixed st. line. Through the fixed point.
Here a fixed point is called vertex, the fixed st. line is called axis, and constant angle known as semi-vertical angle of the cone.
Generator Guiding curve(Base) Semivertical angle
Vertex Axis
|
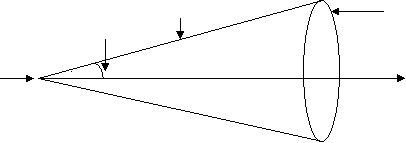
Type III: Equation of Right Circular Cone :
Equation of RCC whose vertex is at (, ,), Semi-vertical angle θ and axis the line
= =
Let P(x, y, z) be any point on given cone
Semivertical angle
A Vertex generator Axis = =
|
The d.r’s of AP (generator) are x – , y – , z –
The dir’s of axis are l , m, n
Since angle between generator AP and axis.
we have,Cosθ =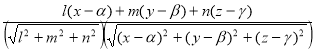
NOTES:
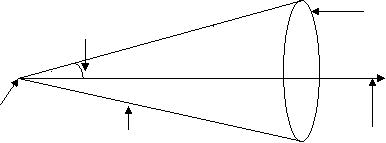
Ex1) Find the equation of Right circular cone whose vertex is at the origin, whose axis is the line = = and which has semi vertical angle of 30.
Sol)
P( x,y,z) Guiding curve(Base)
A Vertex
generator Axis
|
Take any point p(x,y,z) on given cone. The d.r.’s of AP are x, y, z.
The d.r.’s of axis are 1,2,3.
We have cos 30 =
=
i.e. =2x + 4y + 6z
Squaring on both sides we get,
42(x2 + y2+ z2) = (2x + 4y + 3z)2
4 x2 + 16 y2 + 19 z2 – 48xy – 72yz + 36zx = 0
Ex2) Find the equation of right circular cone whose vertex is (1, – 1, 2) and axis is the line
= = and semi vertical angle 45
Sol)
|
|
|
|
A |
Vertex |
generator Axis |
|
Here vertex of cone is P (1, – 1, 2) dr’s of axis are 2, 1, – 2 |
Let Q (x, y, z) be any point on cone. dr’s of PQ are x – 1, y – (– 1), z – 2 |
i.e. x – 1, y + 1, z – 2. |
Since angle between generator PQ and axis is 45 (Given) |
cos 45 = |
= |
Squaring on both sides and simplifying |
9[(x – 1)2 + (y + 1)2 + (z – 2)2] = (2x + y – 2z + 3)2 |
9[(x2 – 2x + 2) + (y2 + 2y + 1) + (z2 – 4z + 4)] |
= 2[4x2 + y2 + 2z2 + 9 + 4xy – 9xz + 12 x – 4yz + 6y – 12z] |
9 x2 + 9 y2 + 9 z2 – 18x + 18y – 36 z + 63 |
= 8x2 + 2 y2 + 8z2 + 8xy – 16xz – 8yz + 24x + 12y–24z + 18 |
x2 + 7y2 + z2 – 8xy + 16 xz + 8yz – 42x + 6y – 12z + 45 = 0. |
Ex3) Find the equation of a right circular cone whose vertex at (1, – 1,1), semi-vertical angle 45 and its axis is perpendicular to the plane 2x + y – 2z + 1 = 0
Sol)
|
|
|
Semivertical angle |
|
A |
Vertex |
generator Axis d.r.’s 2,1, - 2 |
|
|
Since axis of cone is perpendicular to plane 2x + y – 2z + 1 = 0, therefore dr’s of axis are |
2, 1, – 2 . Let Q (x, y, z) be any point on cone. |
dr’s of PQ are x – 1, y + 1, z – 1 |
Angle between any generator say PQ and axis is semi vertical angle which is given to be |
45 |
cos 45 = |
= |
Squaring on both sides and simplifying weget, |
9[(x – 1)2 + (y + 1)2 + (z – 1)2] = 2 (2x + y – 2z + 3)2 |
9[x2 + y2 + z2 – 2x + 2y – 2z + 3] = |
2 [4 x2 + y2 + 4z2 + 9 + 4xy – 8xz + 12x – 4yz + 6y – 12z] |
9 x2 + 9 y2 + 9 z2 – 18x + 18y – 18z + 27 = |
8 x2 + 2y2 + 8z2 + 8xy – 16xz – 8yz + 24x + 12y – 24z + 18 |
x2 + 7y2 + z2 – 8xy + 16 xz + 8yz – 42z + 6y + 6z + 9 = 0 |
Ex4) Find the equation of the cone formed by rotating the ling 2x + 3y = 6 ; z =0 about the y – axis.
Sol)
Given line is 2x + 3y = 6, z = 0 |
These equations can be written as |
2x = 6 – 3y = 3(2 – y), z = 0 |
i.e. = = |
i.e. = = = = |
Since given cone is generated by rotating line = = therefore this line is generator and since this line is rotated about y-axis, therefore y-axis is the axis. Whose dr’s are 0,1,0. |
Semivertical angle is angle between generated and axis which is given by |
cos = |
cos = |
|
P(x,y,z) Guiding curve |
|
A |
Vertex |
generator Axis d.r.’s 0,1,0 |
|
|
|
Let P(x,y,z) be any point on the cone |
dr’s of AP are x – 0, y – 2, z – 0 i.e. x, y – 2, z |
cos = |
– = |
4[x2 + (y – 2)2 + z2] = 13(y – 2)2 |
4[x2 + y2 – 4y + 4 + z2] = 13(y2 – 4y + 4) |
4 x2 – 9 y2 + 4 z2 + 36y – 36 = 0 |
Session 47: Right Circular Cone
NOTES:
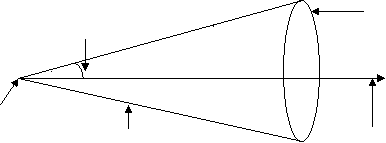
Type III: Equation of Right Circular Cone :
Equation of RCC whose vertex is at (, ,), Semi-vertical angle θ and axis the line
= =
Let P(x, y, z) be any point on given cone
Semivertical angle
A Vertex generator Axis = =
|
The d.r’s of AP (generator) are x – , y – , z –
The dir’s of axis are l , m, n
Since angle between generator AP and axis.
we have,
Cos θ =
Ex6) Find the equation of Right circular cone whose vertex is at the origin, whose axis is the line
= = and which has semi vertical angle of 30.
Sol)
|
|
Semivertical angle |
|
A |
Vertex |
generator Axis |
|
|
Take any point p(x,y,z) on given cone. The d.r.’s of AP are x, y, z. |
The d.r.’s of axis are 1,2,3. |
We have cos 30 = |
= |
i.e. = 2x + 4y + 6z |
Squaring on both sides we get, |
42(x2 + y2+ z2) = (2x + 4y + 3z)2 |
= 4 x2 + 16 y2 + 19 z2 – 48xy – 72yz + 36zx = 0 |
Ex7) Find the equation of right circular cone whose vertex is (1, – 1, 2) and axis is the line = = and semi vertical angle 45
Sol)
|
Semivertical angle |
|
A |
Vertex |
generator Axis |
|
Here vertex of cone is P (1, – 1, 2) dr’s of axis are 2, 1, – 2 |
Let Q (x, y, z) be any point on cone. dr’s of PQ are x – 1, y – (– 1), z – 2 |
i.e. x – 1, y + 1, z – 2. |
Since angle between generator PQ and axis is 45 (Given) |
cos 45 = |
= |
Squaring on both sides and simplifying |
9[(x – 1)2 + (y + 1)2 + (z – 2)2] = (2x + y – 2z + 3)2 |
9[(x2 – 2x + 2) + (y2 + 2y + 1) + (z2 – 4z + 4)] |
= 2[4x2 + y2 + 2z2 + 9 + 4xy – 9xz + 12 x – 4yz + 6y – 12z] |
9 x2 + 9 y2 + 9 z2 – 18x + 18y – 36 z + 63 = 8x2 + 2 y2 + 8z2 + 8xy – 16xz – 8yz + 24x + 12y |
– 24z + 18 |
x2 + 7y2 + z2 – 8xy + 16 xz + 8yz – 42x + 6y – 12z + 45 = 0. |
Ex8) Find the equation of a right circular cone whose vertex at (1, – 1,1), semi-vertical angle 45 and its axis is perpendicular to the plane 2x + y – 2z + 1 = 0
Sol)
|
Semivertical angle |
|
A |
Vertex |
generator Axis d.r.’s 2,1, - 2 |
|
|
Since axis of cone is perpendicular to plane 2x + y – 2z + 1 = 0, therefore dr’s of axis are |
2, 1, – 2 . Let Q (x, y, z) be any point on cone. |
dr’s of PQ are x – 1, y + 1, z – 1 |
Angle between any generator say PQ and axis is semi vertical angle which is given to be 45 |
cos 45 = |
= |
Squaring on both sides and simplifying weget, |
9[(x – 1)2 + (y + 1)2 + (z – 1)2] = 2 (2x + y – 2z + 3)2 |
9[x2 + y2 + z2 – 2x + 2y – 2z + 3] = 2 [4 x2 + y2 + 4z2 + 9 + 4xy – 8xz + 12x – 4yz + 6y – 12z] |
9 x2 + 9 y2 + 9 z2 – 18x + 18y – 18z + 27 = 8 x2 + 2y2 + 8z2 + 8xy – 16xz – 8yz + 24x + 12y – |
24z + 18 |
x2 + 7y2 + z2 – 8xy + 16 xz + 8yz – 42z + 6y + 6z + 9 = 0 |
Ex9) Find the equation of the cone formed by rotating the ling 2x + 3y = 6 ; z =0 about the y – axis.
Sol)
Given line is 2x + 3y = 6, z = 0 |
These equations can be written as |
2x = 6 – 3y = 3(2 – y), z = 0 |
i.e. = = |
i.e. = = = = |
Since given cone is generated by rotating line = = therefore this line is generator and since this line is rotated about y-axis, therefore y-axis is the axis. Whose dr’s are 0,1,0. |
Semivertical angle is angle between generated and axis which is given by |
cos = |
cos = |
|
|
|
Semivertical angle |
|
A |
Vertex |
generator Axis d.r.’s 0,1,0 |
|
|
Let P(x,y,z) be any point on the cone |
dr’s of AP are x – 0, y – 2, z – 0 i.e. x, y – 2, z |
cos = |
– = |
4[x2 + (y – 2)2 + z2] = 13(y – 2)2 |
4[x2 + y2 – 4y + 4 + z2] = 13(y2 – 4y + 4) |
4 x2 – 9 y2 + 4 z2 + 36y – 36 = 0 |
Introduction of Cylinder,Right Circular Cylinder
Cylinder
A cylinder is a surface generated by straight lines which are parallel to a fixed line and satisfies one more condition like intersecting a fixed curve called the guiding curve or directrix or touch a given surface or at fixed distance from the fixed line.
The fixed st. line is called axis of cylinder, the curve (surface) is called guiding curve, variable st. lines are called generators.
Cylinder:
Ex1) Find the equation of cylinder whose generators are parallel to x- axis and which passes through the curve of intersection of the surfaces represented by
x2 + y2 + 2z2 = 12 and x – y + z = 1
Sol)
Since equation of cylinder whose generators from x.
Consider x2 + y2 + 2z2 = 12 (1) x – y + z = 1 (2)
From equation (2) x = 1 + y – z
Using valve of x in equation (1) we get
(1+ y – z)2 + y2 + 2z2 = 12
1 + y2 + z2 + 2y – 2z – 2yz + y2 + 2 z2 = 12
2y2 + 3 z2 – 2yz + 2y – 2z – 11 = 0
Ex2) Find the equation of the cylinder whose generators are parallel to the line = = and whose guiding curve is x2 + y2 = 9, z = 1.
Sol)
Let P(x1,y1,z1) be any point on the cylinder. |
Equation of generator which pas through point P is given by |
= = (1) |
Since guiding curve is |
x2 + y2 = 9; z = 1 |
Put z = 1 in equation (1) we get |
= = |
= x = – x1 + |
x = |
Also = y = y1 + |
= |
Using values of x and y in another equation of guiding curve we get, |
+ = 9 |
|
+ |
Changing x1, y1, z1 to x, y, z respectively |
9x2 + 9y2 + 5z2 + 6xz – 12yz – 6z + 12y – 10z – 76 = 0 |
i.e. |
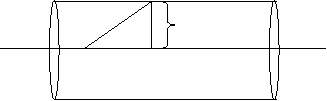
Right circular cylinder:
Right circular cylinder is a surface generated by a strait lines parallel to a fixed st. line and is at a constant distant from it. The fixed st line is called axis and fixed distance or radius of circle is radius of cylinder.
Equation of Right Circular Cylinder: P(x,y,z)
Radius A
|
Let axis of cylinder by = =
Let P(x,y,z) be any point on cylinder. A(, , ) be fixed point axis
PM = radius of cylinder
AP =
AM = Projection of AP on axis
=
From Fig. AP2 = AM2 + PM2
AP2 – AM2 = PM2
(x – )2 + (y – )2 + (z – )2 –
Which is required equation of RC cylinder.
Ex1) Find the equation of the RC cylinder of radius 2 whose axis is the line = = .
Sol)
P(x,y,z) |
|
Radius = 2 |
A |
|
|
|
Let P(x, y, z) be any point on given cylinder. |
The d.r.s of axis are 2,1,2. It’s d.c.’s are , , |
i.e. , , . |
Since axis of cylinder pass through the point A(1,2,3) |
d.r’s of AP ax x – 1, y – 2, z – 3 |
AM = Project of AP on Axis |
AM = (x – 2) + (y – z) + (z – 3) |
From Fig, |
AP2 = AM2+ PM2 |
(x – 1)2 + (y – 2)2 + (z – 3)2 = + 4 |
5x2 + 8y2 + 5z2 - 4yz – 8xz – 4xy + 22x – 16y – 14z – 10 = 0 |
Ex2) The radius of normal section of a right circular cylinder is 2 units, the axis lies along the line. = = , find the equation.
Sol)
P(x,y,z)
Radius = 2
A  M Axis d.r.’s
M Axis d.r.’s
Here (i) dr’s of axis are 2, – 1, 5
(ii) Axis pass through the point A(1, – 3, 2)
(iii)Radius of normal section of right circular cylinder i.e. radius of cylinder is 2
Let P(x,y,z) be any point on given cylinder. From figure
l(AP) = (1) (by distance formule)
l(PM) = 2 (2) (Radius of cylinder)
l(AM) = length of line segment AP on axis
Now dr’s of axis are 2, – 1, 5
dc’s of axis ax , ,
i.e. , ,
l(AM) = (x – 1) – (y + 3) + (z – 2)
l(AM) = (3)
From right angled triangle PMA,
l (AM)2+ l(PM)2 = l(AM)2
+ 2 (2)2 = (x– 1)2 + (y + 3)2 + (z – 2)2
(2x – y + 5z – 15)2 + 120 = 30
4x2 + y2 + 25 z2 + 225 – 4xy + 20xz – 60x – 10yz + 30y – 150 z + 120
= 30 [(x2 – 2x + 1) (y2 + 6y + 9) (z2 4z + 4)]
26 x2 + 29 y2 + 5z2 + 4xy – 20xz + 10yz + 150y + 30z + 75 = 0
Right Circular Cylinder
Problems on Right circular cylinder:
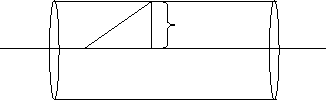
Ex1) Find the equation of right circular cylinder whose axis is the line 2(x – 1) = y + 2 = z and radius is 3.
Sol)
Axis of given right circular cylinder is 2(x – 1) = y + 2 = z which can be |
written as = = |
This line pass through the point say |
A (1, – 2, 0) |
|
|
P(x,y,z) |
|
Radius = 3 |
A |
|
|
|
Axis, = = |
dr’s 1,2,2 |
Let P(x,y,z) ne any point on the cylinder |
l(AP) = (1) |
(∵ by distance formula) |
L (PM) = 3 (2) (Radius of cylinder) |
dr’s of axis are 1,2,2 |
dc’s of axis are , , |
i.e. , , |
Now l(AM) =length of projection of line AP in axis. |
= (x – 1) + (y + 2) + (z – 0) |
|
l(AM) = (3) |
From PMA, |
l(AM)2 + l(PM)2 = l(AP)2 |
+ (3)2 = (x – 1)2 + (y + 2)2 + z2 |
(x2 + 4y2 + 4z2 + 9 + 4xy + 4xz + 6x + 8yz + 12y + 12z) + 81 |
= 9 [(x2 – 2x + 1) + (y2 + 4y + 4) + z2] |
8x2 + 5y2 + 5z2 – 4xy + 4xz +8yz – 24x + 24y – 122 – 90 = 0 |
Ex2) Find the equation of right circular cylinder with radius 2 units, whose axis passes through the point (1,2,3) and has direction consines proportional to 2, – 3, 6.
Sol)
Since direction cosines of axis of dr’s of cylinder is proportional to 2, – 3,6, there for |
dc’s of axis are , , |
i. e. , , |
|
|
P(x,y,z) |
|
Radius = 2 |
A |
|
|
|
l(AP) = (by distance (1) formula) |
l(PM) = Projection of AP on axis |
= (x – 1) + (y – 2) + (2 – 3) |
l(AM) = (3) |
Now From figure |
l(AM)2 + l(PM)2 = l(AP)2 |
+ (2)2 = (x – 1)2 + (y – 2)2 + (z – 3)2 |
|
45x2 + 40 y2 + 13z2 + 12xy – 24xz + 36yz – 42x – 280y -126z + 294 = 0. |
References:
- Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I and II) by P.N. Wartikar and J.N.Wartikar Vidyarthi GrihaPrakashan, Pune.
6. Differential Equations by S. L. Ross (John Wiley and Sons)